REVIEW: Biochemical Effects of Molecular Crowding
N. A. Chebotareva*, B. I. Kurganov, and N. B. Livanova
Bach Institute of Biochemistry, Russian Academy of Sciences, Leninsky pr. 33, Moscow 119071, Russia; fax: (7-095) 954-2732; E-mail: chebotareva@inbi.ras.ru* To whom correspondence should be addressed.
Received July 21, 2004
Cell cytoplasm contains high concentrations of high-molecular-weight components that occupy a substantial part of the volume of the medium (crowding conditions). The effect of crowding on biochemical processes proceeding in the cell (conformational transitions of biomacromolecules, assembling of macromolecular structures, protein folding, protein aggregation, etc.) is discussed in this review. The excluded volume concept, which allows the effects of crowding on biochemical reactions to be quantitatively described, is considered. Experimental data demonstrating the biochemical effects of crowding imitated by both low-molecular-weight and high-molecular-weight crowding agents are summarized.
KEY WORDS: excluded volume, crowding, protein folding, association, denaturation, aggregation
Abbreviations: GAPD) D-glyceraldehyde 3-phosphate dehydrogenase; PDI) protein disulfide isomerase; PEG) polyethylene glycol; TMAO) trimethylamine N-oxide; HbCN) cyanomethemoglobin.
A distinctive property of living systems is that biochemical processes
proceed in a medium containing high concentrations of macromolecules
(50-400 mg/ml) [1-3], the
concentrations of single macrosolute species being not so high.
However, overall the macromolecules present in the cell occupy a
significant part of the total volume of the medium (about 40%).
Therefore, the accessible volume in the cell is reduced. In the
literature, such conditions in the living cell have been termed
“macromolecular crowding”. Figure 1 (see
color insert) demonstrates the crowding conditions in the cytoplasm of
an intact cell [4].
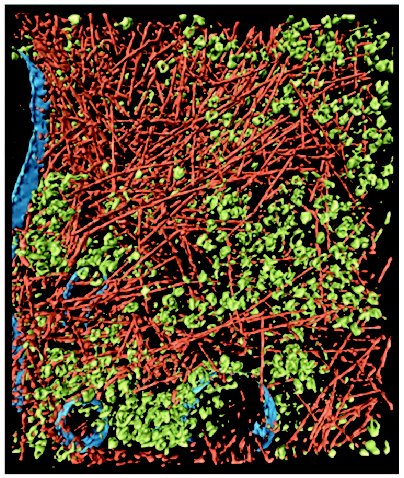
In multicellular organisms, crowding is not confined to cellular interiors, but also occurs in the extracellular matrix of tissues. For instance, cartilage is a biological substance with well pronounced crowding. In blood plasma, the total concentration of macromolecules reaches 80 g/liter, this concentration being sufficient to cause significant crowding effects. A type of crowding designated as a “macromolecular confinement” exists in situations when macromolecules are included in small cellular compartments or pores with dimensions comparable to the size of large macromolecules. Such compartments are created, in particular, in the cytoskeleton lattice or in the central cavity of the chaperonine GroEL [5-7]. When describing the influence of crowding on biological reactions, the following terms are used in the literature: macromolecular crowding, molecular crowding, and also macromolecular confinement, but for all these terms the effect of the excluded volume is implied. The term “molecular crowding” is used when crowded conditions is caused by high concentrations of low-molecular-weight cosolutes (for example, osmolytes).Fig. 1. Crowding conditions in the cytoplasm of an intact motile cell of Dictyostelium discoideum. The cytoplasm is filled with macromolecular components, creating the crowding conditions: actin filaments (reddish), ribosomes and other macromolecular complexes (green), and membranes (blue) (reprinted with permission from article [4], © 2002 AAAS).
The technique of cryoelectron tomography [4, 8] and investigation of the movement of the fluorescent proteins in animal cells [9] are currently used to study crowding in vivo. Direct evidence for the crowded state of cell interiors is provided by the technique of cryoelectron tomography when thin intact cells are frozen rapidly in liquid ethane. This method has unique possibilities for reconstruction of three-dimensional images of the macromolecular complexes in their natural environment. At the present time, a resolution of 5-8 nm has been reached, which is enough for recognition of complexes with dimensions 20-50 nm and for their study in crowded conditions in different cell compartments [8]. The high density of actin filaments (part of the cellular “skeleton”) and ribosomes (Fig. 1) supports the view that cytoplasm is filled with large ensembles of macromolecules, which form functional complexes, rather than with freely diffusing and colliding macromolecules [3, 10]. Direct observation of fluorescent proteins both within the cytosol and inside the cellular compartments shows that their diffusion rate is reduced by factors in the range 3-8 compared to the diffusion rate in solution, which is consistent with predictions of macromolecular crowding theory [9].
Any reaction, which increases the available cellular volume, will be stimulated by crowded conditions. Macromolecular self-association with participation of different macromolecules, protein and nucleic acid folding with formation of the compact structures, the formation of the aggregates and amyloid inclusion bodies in some diseases (Parkinson's disease, Alzheimer's disease, etc.) are such types of reaction.
The goal of the present review is to discuss the influence of crowding on the biochemical processes in the cell.
EFFECTS OF CROWDING ON REACTION EQUILIBRIA AND REACTION RATES
WITH PARTICIPATION OF MACROMOLECULES
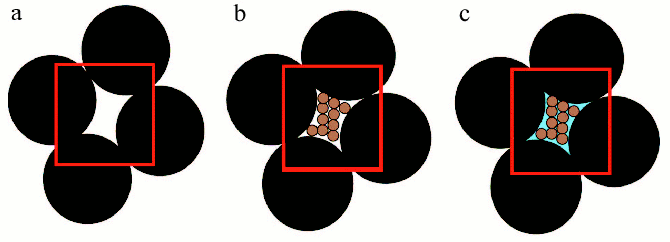
“Macromolecular crowding” is more accurately termed “the excluded volume effect” because its most basic characteristic is the mutual impenetrability of all solute molecules. This nonspecific steric repulsion is always present, regardless of any other attractive or repulsive interactions that might occur between the solute molecules. Thus crowding, like gravity, cannot be excluded and organisms have to cope with its consequences [6, 7]. The influence of the excluded volume on the hydrodynamic and thermodynamic properties of compact globular proteins can be explained using models, which consider protein molecules as hard particles of spherical shape [5]. In order to illustrate the concept of excluded volume, it is possible to employ a macroscopic analogy [11]. Consider a beaker filled to the brim with metallic balls having 5 mm diameter (Fig. 2, reprinted from [11] with permission from Elsevier Publisher). The randomly close-packed ball bearings occupy about 65% of the volume of the beaker, leaving about 35% in the interstices between the ball bearings. Even though the interstitial volume is “empty”, it is impossible to add even a single additional ball bearing of the same size to the beaker with close-packed balls (Fig. 2a, see color insert). In other words, the volume available to ball bearings (i.e., the total volume minus the excluded volume) has become zero. At the same time, the interstitial volume is available to particles that are smaller, for instance, to grains of sand. If we pour sand into the beaker, it will “fill” the interstices between the ball bearings. But in reality, grains of sand could occupy only about 65% of the volume occupied by big balls (Fig. 2b). If the beaker is filled with sand in this fashion, the volume remaining between bearing balls and grains of sand will correspond to about 10% of the total volume of the beaker. This part of the volume is excluded to both ball bearings and grains of sand, but may be occupy by the particles of the smaller size, for example, by molecules of water (Fig. 2c).
Volume exclusion and thermodynamic activity of a substance. Consider the effect of macromolecular crowding on the thermodynamic activity of a substance. The chemical potential of solute species i can be partitioned into ideal and nonideal contributions:Fig. 2. Scheme illustrated the concept of excluded volume. Large black spheres depict big ball-bearings, smaller brown spheres depict grains of sand, and blue field indicates water. The red border demarcates a region of unit volume (reprinted with permission from article [11] ©?2003 Elsevier).
The ideal contribution is the free energy change expected in the absence of solute-solute interactions:
where µi0 is the standard state chemical potential of species i, k is Boltzmann's constant, T the absolute temperature, and ci the concentration (in molar or w/v units). The nonideal contribution is the free energy change associated with the equilibrium free energy of nonspecific interaction between a molecule of solute species i and all other solute molecules in the solution:
where gammai is the activity coefficient. Equations (1)-(3) can be transformed into the following:
where ai = gammaici is an effective concentration called the thermodynamic activity.
It is essential to keep in mind that the theory of chemical equilibrium is based upon the use of activities rather than concentrations. In a very dilute solution, the non-ideal contribution of the chemical potential can be neglected, and concentrations can be used instead of activities. In a crowded biological medium, the activity of some species could significantly exceed their respective concentration [6, 7].
The theoretical aspects of the effect of excluded volume on chemical reaction were discussed by Minton and coworkers, Ellis and coworkers, Winzor and coworkers, and many others [11-19]. Consider a generalized reversible reaction in solution:
where ri is the stoichiometric coefficient of reactant species Ri and pi is the stoichiometric coefficient of product species Pi. The equilibrium molar concentrations of reactants are related by following relationship:
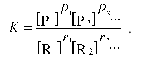 (6)
(6)Here K denotes the equilibrium constant, which under crowding conditions should be considered as an apparent constant related to the true equilibrium constant K0 by the equation:
where Gamma is the “nonideality factor”. The value of Gamma could be expressed via the thermodynamic activity coefficients gammai for each i-th component:
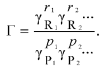 (8)
(8)To explain the thermodynamic nonideality initiated by crowding on the rates of the forward and backward reaction the theory of absolute reaction rates could be used [20]. For the values of the effective forward and backward reaction rate constants (kf and kb, respectively) the following expressions should be written:
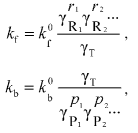 (9)
(9)where kf0 and kb0 denote, respectively, the forward and backward rate constants in the infinitely dilute solution of all macrosolutes, and gammaT denotes the thermodynamic activity coefficient of the transition-state complex.
In a solution containing macromolecules that interact exclusively via steric repulsion, a very simple relationship exists between the effective and the real concentration of each solute:
where ai and ci are the thermodynamic activity and concentration of the solute i, respectively; nutot is the total volume; and nua,i is the volume available to the solute i. From the practical point of view it is very important that usually the activity coefficients of the proteins could be calculated rather exactly using simple structural models, where the hard globular proteins are represented by hard spherical or spherocylindrical particles [13, 21-23]. Evaluating in such a way the activity coefficients of proteins and other macromolecules and the value of nonideality factor Gamma under crowding conditions, it is possible to predict the effect of crowding on the equilibrium position and the rates of the reactions proceeding with the participation of the biomacromolecules [11].
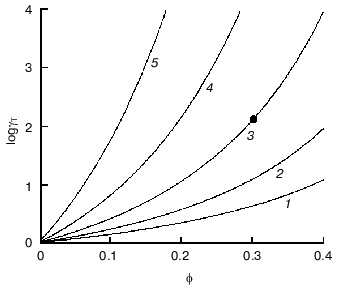
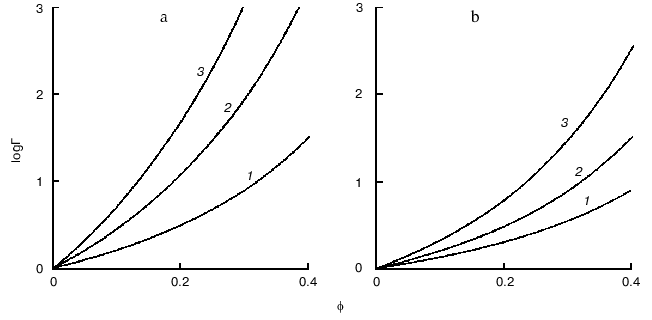
To imagine how strong could be deviations from ideality under crowding conditions, let us evaluate the activity coefficient of a globular test-protein T in a solution containing a second globular protein C, which could be called a crowding agent. Let us denote as phi the fraction of the total volume that is occupied by crowder. Both test-protein and protein crowding agent are considered as hard spherical particles with molecular masses strictly proportional to the particle radius in third degree. Figure 3 presents the theoretical dependence of the activity coefficient of the test-protein T (gammaT) on phi value, increasing with the filling of volume by the crowder. The dependence of loggammaT on phi is calculated under the different relationships of the particle masses MT/MC (MT and MC are the masses of test-protein and crowding agent, respectively). As shown in the figure, the activity coefficient of test-protein T could be several orders of magnitude higher than the value in very dilute solutions (gammaT = 1) at the level of volume occupancy by crowding agent corresponding to physiological conditions. For example, the dark circle in the Fig. 3 indicates that at phi = 0.3 the value of the activity coefficient of the test-protein T exceeds 100. This value of gammaT is close to the experimentally measured activity coefficient of hemoglobin in a 350 g/liter solution comparable to its content in a red blood cell.
Let us discuss now the influence of crowding on reversible protein isomerization:Fig. 3. Dependence of logarithm of activity coefficient (gammaT) of spherical particles of species T with mass of MT plotted as a function of phi, the fractional occupancy of volume of the crowding agent C with mass of MC [11]. The dependence of loggammaT on phi is calculated at different values of MT/MC: 0.1 (1), 0.3 (2), 1 (3), 3 (4), and 10 (5).
where R and P are conformational states of the protein molecule that are distinguished by the volume (the compactness degree). Allosteric transitions of proteins induced by the binding of allosteric ligands and reversible protein denaturation are, in particular, such kinds of processes. Processes of this type are accompanied by a change in the compactness of the protein molecule. In a very well known model of allosteric proteins proposed by Monod, Wyman, and Changeux [24], the equilibrium between “relaxed” protein conformation R, stabilized by substrates and allosteric activators, and “tense”, more compact conformation T, stabilized by allosteric inhibitors, is considered.
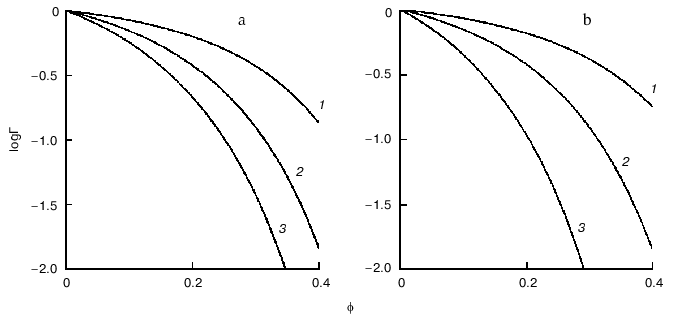
Figure 4 demonstrates the shift of equilibrium (11) in the presence of macromolecular crowding agent (C). All macromolecular substances (R, P, and C) are considered as hard spherical particles. The situation is discussed when the conformational transition in the model protein is accompanied by an increase in the effective volume of the molecule, i.e., the radius of the particle P (rP) exceeds the radius of the particle R (rR). Such a situation occurs, for instance, under the unfolding (denaturation) of a protein molecule or under the allosteric transition of the form T into the form R. The nonideality factor Gamma = gammaR/gammaP < 1. The higher is the part of excluded volume occupied by the crowding agent phi, the more the nonideality factor Gamma deviates from unity. Figure 4a illustrates the enhancement of the crowding effect on the increase in the ratio of the protein molecular radii rP/rR. Figure 4b shows that the crowding effect is more pronounced with increase in the relative size of the model protein, i.e., at the increase in the ratio of the macromolecules volumes of the model proteins and crowding agent vR/vC [11].
Consider the influence of crowding on the reversible association of protein moleculesFig. 4. Influence of crowding on the reversible conformational transition of proteins R <--> P [11]. a) Dependence of the nonideality factor Gamma on the fraction of volume occupied by the inert crowding agent C (phi), at different values of the relationship rP/rR (rP and rR are radii of protein molecules P and R, respectively): 1.1 (1), 1.2 (2), 1.3 (3). The volumes of the macromolecules R and C (vR and vC, respectively) are assumed to be equal. b) Dependence of the nonideality factor Gamma on phi at different values of relationship nuR/nuC. The relationship rP/rR is assumed to be equal to 1.2.
where R is monomer and P is oligomer composed from n monomers. The behavior of the associating enzyme system under crowding conditions is presented in Fig. 5. It is supposed that all macrosolute species (R, P, and C) can be represented as hard spherical particles, and that the volume of the oligomer P is equal to n times the volume of monomer R. The nonideality factor Gamma = gammaRn/gammaP. The activity coefficient for the monomer gammaR is less than the activity coefficient for the oligomer gammaP. However, because n > 1, the magnitude of the nonideality factor Gamma is higher than unity. The higher is the part of the excluded volume occupied by crowder, phi, the stronger is the deviation of the nonideality factor Gamma from unity. Figure 5a illustrates the enhancement of the crowding effect on the increase in the number of monomers involved into association (i.e., increase in the value of n). Figure 5b shows that the crowding effect is more pronounced on the increase in the relative dimensions of the model protein, i.e., on the increase in the ratio of the volume of the model protein macromolecules to the volume of the crowding agent nuR/nuC [11].
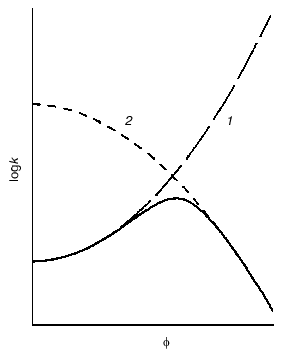
Crowding has a complex effect on the rate of biochemical reactions. On one hand, under crowding conditions the thermodynamic activities of the reactants increase, and, on the other hand, crowding reduces diffusion, and, therefore, the possibility of the meeting of two reactants decreases. The overall result of these opposing factors depends on the nature of each reaction. The decrease in the diffusional mobility of the macromolecules in the medium characterized by high viscosity should lead to a decrease in the rates of biochemical reactions in which several macromolecules are involved (association and aggregation of the macromolecules). Theoretical analysis of the influence of crowding on the rate of association of macromolecules carried by Minton [25] showed that at small magnitudes of the fraction of the volume that is occupied by crowder phi, the rate of association increased with increasing value phi. However, at rather high phi values the rate of association begins to decrease owing to increase in the viscosity of the medium (Fig. 6) [25].Fig. 5. Effect of crowding on the reversible association of proteins nR <--> P [11]. a) Dependence of the nonideality factor Gamma on the fraction of volume occupied by the inert crowding agent C (phi). at different values of n: 2 (1), 3 (2), 4 (3). The volumes of the macromolecules R and C (nuR and nuC, respectively) are assumed to be equal. b) Dependence of the nonideality factor Gamma on phi at different values of the relationship nuR/nuC: 0.3 (1), 1 (2), 3 (3). The value of n is assumed to be equal to 2.
Fig. 6. Schematic representation of the dependence of the rate constant k for macromolecule association on the fraction of volume occupied by inert crowding agent phi (solid line) [25]. The dotted line 1 is the dependence of logk on phi, expected with consideration of the excluded volume; line 2 is the dependence of logk on phi with consideration of the influence of viscosity on the rate of macromolecule association.
EXPERIMENTAL DATA ILLUSTRATING THE EFFECT OF MACROMOLECULAR CROWDING ON BIOCHEMICAL REACTIONS
Molecular crowding could have a strong effect both on the equilibrium and on the rate of reactions involving macromolecules [5-7, 20, 26, 27]. It should be noted that properties and interaction of macromolecules in biochemical experiments in vivo are usually studied in dilute solutions (lower than 0.1 g/liter), where the effect of crowding can be neglected. To understand the biochemical processes, which proceed in the living cell, the crowding conditions should be simulated in experiments in vitro.
To simulate macromolecular crowding in vitro, crowding agents should be added to the solution. The essential feature required of the macromolecular crowders are the following: their molecular mass should range from 50 to 200 kD, the molecules should have the shape of globules to avoid making the solution too viscous, the crowding molecules should not have the ability for specific interactions with the molecules under test, because crowding implies only steric repulsion between different molecules. This last requirement is the most difficult to meet and, in practice, it is necessary to compare the action of several crowding agents. The most commonly used crowding agents are BSA, ovalbumin, Ficoll 70, and polyethylene glycol (PEG). When PEG is used as a crowder, we should pay attention to the data of Farrugia et al. [28], who studied the interaction of BSA and PEG with different molecular masses and concluded that low-molecular-weight PEG (for instance, PEG 600) interacted with BSA through van der Waals forces between the hydrophobic surfaces, whereas on the use of high-molecular-weight PEG the effect of excluded volume prevailed. Thus, the low-molecular-weight PEG could not be a “pure” crowding agent. As shown in another paper [29] studying the interaction of human serum albumin with PEG of molecular weights 8000 and 10,000 daltons, the molecules of the high-molecular-weight PEG have a stabilizing effect on the native compact protein structure. The interaction between these polymers and the protein is thermodynamically unfavorable both for the native and for the denatured state of albumin. At the same time, the molecules of low-molecular-weight PEG (1000 and 4000 daltons) at low temperature are excluded from the native state of the protein, and at high temperature they preferably interact with BSA. This means that low-molecular-weight PEG is not a proper crowding agent for study of the effect of crowding on thermal denaturation and refolding.
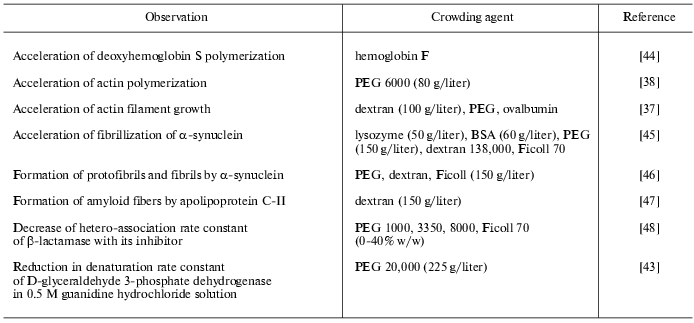
Experimental data on the influence of macromolecular crowding on the equilibrium and rates of such biochemical reactions as protein association, reversible denaturation and folding, polymerization of actin, assembly of protofibrils, etc., studied in model systems in vitro, are summarized in the Tables 1 and 2. In all cases, the addition of inert macromolecules (crowding agents) enhanced interaction, increased reaction rates, or shifted the equilibrium to association [5, 6, 11, 26].
Table 1. Experimentally observed effects of
macromolecular crowding on equilibrium of biochemical reactions

Table 2. Effects of macromolecular crowding
on biochemical reaction rates
New methodical approaches have been developed to study macromolecular crowding. The measurement of sedimentation equilibrium is one of the most powerful methods for the quantitative estimation of macromolecular associations in solution [33, 49, 50]. The power of the method resides, first, in the ability of the centrifuge to discriminate between various molecular species on the basis of differences in buoyant mass, and, second, in the rigorous thermodynamic formulation of sedimentation equilibrium. The method was used widely for ideal solutions, but it was poorly suited for the study of the properties of a dilute protein in a solution containing high concentrations of other proteins. Rivas, Fernandez, and Minton [33, 34] developed a theory of sedimentation equilibrium of highly non-ideal solutions using labeled macromolecules. The proposed method, called “nonideal tracer sedimentation equilibrium” (NITSE), permits the simultaneous measurement of the equilibrium distribution of labeled dilute tracer proteins and unlabeled, highly concentrated “background” macromolecules together in solution to be carried out [33, 34, 50]. The method can be utilized for the measurements of self- and hetero-association of dilute tracer protein in high concentration solution of background macromolecules. The NITSE method was used to study self-association of the bacterial cell division protein FtsZ and to measure the effect of high concentrations (up to 150 g/liter) of each of two inert proteins, cyanomethemoglobin (HbCN) and BSA, on the state of association of FtsZ. Under conditions inhibiting (in the absence of Mg2+) FtsZ self-association, the dependence of the apparent buoyant molar mass of diluted FtsZ on the concentration of BSA and HbCN up to 150 g/liter is well accounted for by a simple model of steric repulsion in which both crowding species and FtsZ are represented by effective hard spherical particles with size close to those of the respective molecules. Under conditions in which FtsZ self-associates (in the presence of GDP and Mg2+), the dependence of the apparent buoyant molar mass of diluted FtsZ on the concentration of both FtsZ (up to 1 g/liter) and BSA or HbCN (up to 150 g/liter) is well accounted for by a simple model for steric repulsion in which both crowder and monomeric FtsZ are represented by the same effective hard spherical particles, and each oligomer is represented by an effective hard spherocylinder with a cylindrical radius approximately equal to that of the monomer and a length varying linearly with the number of protomers in accordance with conservation of volume. The results obtained [34] provide direct evidence that excluded volume effects can significantly promote the self-assembly of proteins in macromolecularly crowded solutions.
To imitate the conditions of molecular confinement, the sol-gel method of protein encapsulation into hydrated pores of silica gel matrix of silicic acid is used [51]. Theory predicts that such confinement will stabilize more compact protein structure. This prediction is confirmed by the fact that thermostability of proteins (lysozyme, alpha-lactalbumin, apomyoglobin) in pores is significantly increased [51]. The merit of this approach in studies of protein denaturation is that the undesirable aggregation of unfolded forms of protein molecules is excluded.
Molecular crowding and chaperones. The existence of crowding in living cells is a possible reason for the presence of chaperones for the correct folding of nascent polypeptide chains. Since pioneering studies of Aaron Klug [52] and Christian Anfinsen [53] the view existed that the correct folding of polypeptide chains into the functional protein structure proceeds spontaneously and depends only on their amino acid sequence, and in this case both the primary translation products emerging from polysomes and partly folded polypeptide chains arising as a result of denaturation have ability for self-assembly. This view was challenged by the discovery of molecular chaperones, a class of unrelated proteins that share the property of assisting the assembly of other protein structures without being present in the final functional form of these structures [54, 55]. Crowding prevents the self-assembly of partly folded polypeptide chains, stimulating the interaction between exposed hydrophobic surfaces of different chains, thus increasing the propensity of these surfaces to bind to one another [56, 57]. In vitro such an aggregation could be decreased by simple dilution of the solution. In a living cell crowding conditions stimulate the association of the chaperones with partially folded polypeptide chains which cause the shielding of the hydrophobic surfaces and thus preventing the binding of the polypeptide chains with each other. The system of chaperonines GroEL-GroES prevents the aggregation of primary translation products and helps them to fold effectively in bacterial cytosol [58-60]. GroEL consists of two heptameric rings, each collected from subunits with molecular mass ~57 kD and each ring containing inside the cavity the hydrophobic binding regions. GroES consists of one ring of seven subunits with molecular mass ~10 kD each. The folding of the polypeptide chain proceeds in the cavity of GroEL in the presence of GroES and ATP. GroES acts as a cap on the Anfinsen cage and prevents the diffusion of partly folded polypeptide chains into the cytoplasm. Inside the closed cage folding proceeds during tens of seconds at 37°C, i.e., for a length of time that is set by an ATPase activity that releases GroES. However if polypeptides fold slowly, their release into the cytoplasm is possible before the finishing of the folding, which causes their aggregation. The release of polypeptide is prevented by the addition of crowding agents (200 g/liter); instead, the polypeptide rebinds to the same GroEL oligomer, which allows the assembly to be finished [61, 62]. Martin [62] showed that the proteins such as dihydrofolate reductase from mouse, enolase from yeast, and green fluorescent protein from beef liver, which can fold spontaneously in the diluted solutions, loose this capability under the conditions of macromolecular crowding imitated by Ficoll 70 (28%). Refolding of these proteins, which were previously denatured in 5.3 M guanidine hydrochloride, becomes dependent on the GroEL-GroES chaperonine system and ATP. A comparison of the rate of folding in the presence of GroEL, GroES, and ATP showed that green fluorescent protein folds in the solution of Ficoll 70 with t1/2 = 33 sec, and in dilute buffer with t1/2 = 20 sec. Such a difference in the refolding kinetics for enolase and dihydrofolate reductase under the same conditions was not shown. These experiments have demonstrated the participation of the chaperons in the correct folding of the proteins under crowding conditions [62]. The effect of crowding agents (PEG 20,000, dextran 70, and BSA) on the folding in the presence of GroEL of D-glyceraldehyde 3-phosphate dehydrogenase (GAPD), which was completely denatured in the presence of 0.5 M guanidine hydrochloride, was demonstrated by Ren et al. [43]. Chaperone helps the refolding of GAPD, and the presence of crowders increases its effect.
The mechanisms of action of various chaperons are quite different. In particular, the enzyme protein disulfide isomerase (PDI) has a chaperone function. As was shown for hen lysozyme, the chaperone function of this enzyme is strongly enhanced under crowding conditions [63]. Hen lysozyme provides a good test system because it can be produced in two states but with very different aggregation tendencies: one is termed the oxidized state (as two disulfide bonds are present) and the other is termed the reduced state (where these bonds are in the thiol form). Refolding of oxidized lysozyme proceeds very quickly, and the addition of a crowding agent has practically no influence on this process. Refolding of the reduced lysozyme proceeds very slowly, which results in its aggregation under crowded conditions. However, if PDI is included into the refolding buffer besides crowding agent, the refolding is accelerated significantly with simultaneous increase in its yield. Evidently, the chaperone activity of PDI is enhanced under the crowding conditions. Thus, the application of crowding theory to aggregation allows two predictions to be made: 1) crowding should favor aggregation, and 2) crowding should increase the functional activity of chaperones [7].
MOLECULAR CROWDING INDUCED BY OSMOLYTES
In response to stress (osmotic, chemical, or thermal), many living organisms accumulate high concentrations of osmolytes. Osmolytes are small organic molecules, such as polyols, some amino acids, and methylamines. They protect proteins under stress conditions by stabilization of protein structure [64-68]. For instance, the tissues of sharks and rays contain urea in high concentration. It is known that urea causes denaturation of the proteins, but this effect could be compensated through supporting of the high concentration of the counteracting osmolytes, especially trimethylamine N-oxide (TMAO), betaine, and sarcosine [64-68]. Among organisms concentrating proline are those that have adapted to live in high salt environments, and they use this osmolyte to offset the high external osmotic pressure [65]. Such polyols as sucrose probably have selective ability to stabilize proteins at extremes of temperature [65, 67].
Much experimental data has accumulated on the protective action of osmolytes [67-76], but the molecular mechanisms of their action are not clear. The same experimental data can be explained very often using contradictory molecular mechanisms [19]. Let us discuss the effect of molecular crowding arising from the high concentrations of osmolytes on biochemical reactions (association, isomerization, protein folding and aggregation, interaction of macromolecules with ligands, etc.).
Molecular crowding could displace the equilibrium of reversibly associating protein towards the high-molecular-weight state, and the extent to which it influences the equilibrium state depends on the concentration of the inert cosolute [77-80]. For example, in the case of enolase, which reversibly associates as monomer-dimer, increase in the dimer fraction with increasing sucrose concentration has been observed [78]. The fact that low-molecular-weight species can also participate in the effects of excluded volume is demonstrated by a three-fold increase of dimerization constant for alpha-chymotrypsin in the presence of 0.15 M sucrose [77]. Similar effects have been observed also for DNA-protein interactions [81, 82]. Carner and Rau [81] discovered a multiple increase in the constant of binding of Gal repressor with DNA in the presence of sucrose, betaine, or triethylene glycol. Poon and coworkers [82] showed an increase in the apparent constant of binding of the regulatory protein TyrR with DNA in the presence of sucrose and triethylene glycol. In paper [83], the sedimentation equilibrium method was used to quantify the action of high concentrations of glucose, sucrose, and raffinose on the reversible dimerization of alpha-chymotrypsin. The dimerization constant (K2) was calculated from the sedimentation equilibrium distributions of the enzyme in the absence of osmolytes and the apparent dimerization constant (K2,app) was calculated in the presence of osmolytes. To quantify the effect of osmolytes on the dimerization reaction, the dependence (lnK2,app) was plotted against the molar sugar concentration (Cs), which appeared to be linear. To explain the effect of stabilization of the dimer of alpha-chymotrypsin and to compare two models that interpret the effect of osmolytes either as a weak interaction (a preferential binding) or as a steric repulsion (effect of excluded volume), the authors used the magnitude deltalnK2,app/deltaCs (M-1). This experimentally evaluated value was compared with the value calculated from the models. It was shown that weak interactions suppose the deltalnK2,app/deltaCs value to be less than that observed, whereas predictions based on the theory of excluded volume gives the deltalnK2,app/deltaCs value exceeding this value. However, the theory of excluded volume predicts rather well the linear dependence of lnK2,app on Cs and a change in the slope of lnK2,app on Cs with increase in the sugar molecule size. To evaluate the expected effect of molecular crowding, the following equations were used in [83]:
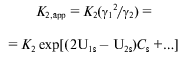 (13)
(13)or in logarithmic form:
where the second virial coefficient (U1s for monomer and U2s for dimers) is expressed via excluded covolume (in the absence of charge on sucrose). Stabilization parameter deltalnK2,app/deltaCs is equivalent to the difference in 2U1s - U2s.
Under the assumption of spherical shape of alpha-chymotrypsin monomer and saccharide, U1s can be calculated as 4piN(r1 + rs)3/3, where N is Avogadro's number, enzyme monomer radius r1 is equal to 2.44 nm [77, 84], radii rs are equal to 0.25 nm for glucose, 0.34 nm for sucrose, and 0.43 nm for raffinose [83]. The value of U2s can be calculated by approximating the protein dimer through the ellipsoid of rotation with the ratio of the axes equal to 2 [85, 86], and using the equation:
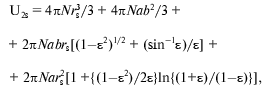 (15)
(15)where epsilon2 = 1 - (b/a)2, b = r1, a = 2r1.
In comparing the experimental and calculated values, the authors of paper [83] concluded that molecular crowding plays the major role in the enhancement of alpha-chymotrypsin dimerization. In article [79], the sedimentation velocity method was used to quantify the effect of high concentrations of TMAO on the self-association of glycogen phosphorylase b (from rabbit skeletal muscle) induced by 1 mM AMP. Phosphorylase b associates reversibly in a dimer-tetramer equilibrium, which can be considered as a reaction of the dimerization of dimers. To quantify the effect of osmolyte on the reaction of dimerization, the dependence of the logarithm of the apparent association constant (lnK2,app) on the molar concentration of the osmolyte (Cosm) was plotted, which appeared to be linear. To evaluate the expected effect of molecular crowding, relationships similar to those given above (14) were used in paper [79]:
where the second virial coefficient (B2,osm for dimer and B4,osm for tetramer) is expressed by the covolume excluded. The values of B2,osm and B4,osm could be calculated through approximation of the protein dimer and tetramer by the ellipsoid of rotation with an axial ratio of 1.9 and using Eq. (15) [85, 86]. The comparison of the value deltaln[(K2,4)app/K2,4]/deltaCosm (M-1) obtained experimentally with the calculated value showed that the theory of excluded volume predicts a larger effect than that which was observed. The association constant K2,4 for dimer-tetramer equilibrium in the presence of 1 M TMAO increases 2-fold. For explanation of the data, a reversible stage of dimer isomerization, which is preceded by association, was introduced. The small enhancement of the association degree of phosphorylase b in the presence of TMAO as compared with the theoretical predictions means that the effect of excluded volume on the dimer-tetramer equilibrium is compensated by the shift of equilibrium in the isomerization reaction of the dimer T <--> R towards the more compact, non-associating T-conformation [79].
The influence of TMAO on the self-association of phosphorylase kinase from rabbit skeletal muscle has been studied by sedimentation velocity and turbidimetry [80]. It was shown that TMAO (0.6-1.0 M) stimulates the association of phosphorylase kinase induced by Ca2+ and Mg2+. In the presence of TMAO, besides associates consisting of relatively small number (n) of enzyme molecules (n = 2, 3, 4, ...), large associates with sedimentation coefficient s20,w = 189 and 385 S corresponding to 24- and 70-mers of phosphorylase kinase were registered. The initial rate of association increased nonlinearly with increasing osmolyte concentration (0.4-1.4 M).
A stabilizing effect of glycerol on the thermal inactivation and denaturation of creatine kinase was shown by differential scanning calorimetry [87]. Glycerol increases the temperature of denaturation of the enzyme (Tm). A stabilizing effect of 1 M glucose on the structure of acid-denatured ferricytochrome c was shown by Morar et al. [88]. The unfolded protein folded until the size and shape of native cytochrome c was achieved in the presence of 1 M glucose.
In review [19] the protective action of polyols [89] on the isomerization equilibrium between folded (F) and unfolded (U) protein states is considered in detail. Protein stability is defined as the free energy change associated with the reaction F <--> U: DeltaG0 = -RTlnK; where equilibrium constant K = CF/CU for dilute solution, CF and CU are the concentrations of folded and unfolded protein state, respectively. In the presence of the high concentrations of osmolytes the apparent isomerization constant was Kapp = CF/CU. The protective effect of osmolyte is characterized as DeltaDeltaG0/RT = ln(K/Kapp). To compare the effects of different osmolytes on the isomerization reaction, ln(Kapp/K) values were plotted against molar sugar concentration Cosm. Because all the plots are linear, their slope [deltaDeltaDeltaG0/deltaCosm] can be used as a measure of protein stabilization. Stabilization increases with increasing size of sugar during the transition from mono- to tetrasaccharide (glucose --> trehalose --> melesitose --> stachiose) [19]. The models based on the concepts of thermodynamic non-ideality (effects of excluded volume and preferential hydration) and also the models considering the preferential interaction of protein with osmolyte are reviewed in [19] for explanation of the effect of osmolytes. The comparison of experimental and theoretical data showed that the deltaDeltaDeltaG0/deltaCosm value calculated on the basis of excluded volume theory exceeds the experimental value, and the other models give underestimated value of deltaDeltaDeltaG0/deltaCosm. Despite the fact that the degree of the displacement of equilibrium isomerization is not always equivalent to the effect predicted on the basis of the excluded volume, the authors of the work [19] supposed that the effect of molecular crowding plays an important role in protein stabilization.
In papers [90, 91], the effect of molecular crowding on the kinetics of allosteric enzymes has been studied. For reactions involving enzyme isomerization, be it preexisting [24] or substrate-induced [92], a crowded molecular environment should favor the smaller isomeric state. Thus, it was shown that the kinetics of pyruvate kinase inhibition by phenylalanine is sigmoid, and after addition of 0.1 M proline, the sigmoid shape disappears [91]. Using difference sedimentation velocity analysis authors [91] showed that in the presence of allosteric inhibitor the sedimentation coefficient of the enzyme decreases, and on the addition of proline this difference disappears, which is indicative of the displacement of equilibrium between the enzyme isomers towards the more compact state.
Two kinds of models have been used in the literature for description of the interactions between osmolytes and proteins. One kind is based upon the effects of excluded volume, and the other took into account the binding of proteins with osmolytes. Weatherly and Pielak [93] studying the interactions of osmolytes with ferricytochrome c as a model protein concluded that the simple model cannot explain the interaction between osmolytes and proteins and interpreted the second virial coefficient as a measure of interactions of the excluded volumes and protein binding with osmolyte [93].
It should be noted that some researchers interpret the influence of osmolytes on biochemical reactions in terms of statistical mechanics using the theory of excluded volume and calculating the second virial coefficients, which characterize the interactions of the molecules in solution [14-18, 82-84, 90, 91, 94-96]. Other researchers operate with the terms of preferable hydration of the protein and the free energy [66, 67, 69-71, 97-101]. Winzor and Wills analyzed both approaches and showed that they are practically equivalent [14, 17].
The mechanism of the protective effect of osmolytes counteracting urea was studied with different model systems. It was shown that the influence of “counteracting” osmolytes had a general character and was propagated on proteins, which were not exposed to urea in vivo [66, 68]. Thus, Burg and Peters [68] showed that urea reduced the thermostability of ribonuclease A, whereas glycerophosphocholine and TMAO compensated this effect. It was demonstrated [64, 102] that TMAO and beta-alanine had stabilizing effects on the structure of ribonuclease A, increasing its temperature of denaturation Tm. Data obtained by NMR spectroscopy showed that the activity of ribonuclease A decreased in the presence of urea and was completely restored on the addition of TMAO to urea (optimal ratio [urea]/[TMAO] is 1 : 1). Bolen and coworkers [101] showed that reduced carboxyamidated ribonuclease A (RCAM) exists in the unfolded state in the presence of urea and refolds on the addition of stabilizing osmolytes (TMAO, sarcosine, sucrose, and proline). During refolding of the reduced carboxyamidated ribonuclease T1 a more pronounced effect of osmolytes, favoring the protein refolding, was observed in the order TMAO > sarcosine > sucrose > proline, where TMAO is the more effective osmolyte and proline is the less effective one [67]. The proteins are thermodynamically more stable in the presence of osmolyte than in water solution, because osmolytes increase Gibbs energy for the denatured state much stronger than for the native state [67, 70, 71, 101, 103]. Bolen and Baskakov [67] named the non-favorable interactions between osmolyte and polypeptide backbone as an “osmophobic effect”. Since the peptide backbone is highly exposed to osmolyte in the denatured state, the osmophobic effect preferentially raises the free energy of the denatured state, shifting the equilibrium in favor of the native state.
Effects of hydration are very important also on protein polymerization, when osmolytes are excluded from the nearest environment of the protein surface due to protein-protein interactions and, in particular, can accelerate the assembly of microtubules and increase their stability [104]. Yang et al. [105] showed that TMAO and glycerol accelerate the main steps in the amyloidal pathway (early nucleation, conformational changes, and also the protofibril-fibril transformation).
It should be noted in conclusion that crowding affects all biochemical processes where changes in excluded volume are observed. The collapse of newly synthesized polypeptide chains into compact functional proteins, protein unfolding, induced by chemical or thermal stress, the formation of oligomeric structures and multienzyme complexes in metabolic pathways, the aggregation of proteins into nonfunctional aggregates, such as bacterial inclusion bodies and plaques in human amyloid diseases (Parkinson's and Alzheimer's diseases), are related to similar processes. To imitate the conditions in vivo during the study of biochemical reactions in vitro, crowding agents should be used. Such experiments allow conclusions about the influence of crowding on biochemical processes occurring in the cell to be made.
This work was supported by the Russian Foundation for Basic Research (grants 02-04-49099 and 02-04-48704), the Program for Fundamental Research “Molecular and Cell Biology” of the Russian Academy of Sciences, the Program for the Support of the Leading Scientific Schools Minpromnauka RF (grant 813.2003.4), and by INTAS (grant 03-51-4813).
REFERENCES
1.Fulton, A. B. (1982) Cell, 30,
345-347.
2.Zimmerman, S. B., and Trach, S. O. (1991) J.
Mol. Biol., 222, 599-620.
3.Ellis, R. J., and Minton, A. P. (2003)
Nature, 425, 27-28.
4.Medalia, O., Weber, I., Frangakis, A. S., Nicastro,
D., Gerisch, G., and Baumeister, W. (2002) Science, 298,
1209-1213.
5.Zimmerman, S. B., and Minton, A. P. (1993) Annu.
Rev. Biophys. Biomol. Struct., 22, 27-65.
6.Minton, A. P. (2001) J. Biol. Chem.,
276, 10577-10580.
7.Ellis, R. J. (2001) Trends Biochem. Sci.,
26, 597-604.
8.Grunewald, K., Medalia, O., Gross, A., Steven, A.,
and Baumeister, W. (2003) Biophys. Chem., 100,
577-591.
9Verkman, A. (2002) Trends Biochem. Sci., 27, 27-33.
10.Lyubarev, A. E., and Kurganov, B. I. (1996) in
Organization of Biochemical Systems: Structural and Regulatory
Aspects (Kurganov, B. I., and Lyubarev, A. E., eds.) Nova Science,
N. Y., pp. 1-81.
11.Hall, D., and Minton, A. P. (2003) Biochim.
Biophys. Acta, 1649, 127-139.
12.Minton, A. P. (1981) Biopolymers,
20, 2093-2120.
13.Minton, A. P. (1983) Mol. Cell. Biochem.,
55, 119-140.
14.Wills, P. R., and Winzor, D. J. (1993)
Biopolymers, 33, 1627-1629.
15.Wills, P. R., Comper, W. D., and Winzor, D. J.
(1993) Arch. Biochem. Biophys., 300, 206-212.
16.Winzor, C. L., Winzor, D. J., Paleg, L. G.,
Jones, G. P., and Naidu, B. P. (1992) Arch. Biochem. Biophys.,
296, 102-107.
17.Winzor, D. J., and Wills, P. R. (1995) in
Protein-Solvent Interactions (Gregory, R. B., ed.) Marcel Dekker,
N. Y., pp. 483-520.
18.Winzor, D. J., and Wills, P. R. (1995)
Biophys. Chem., 57, 103-110.
19.Davis-Searles, P. R., Saunders, A. J., Erie, D.
A., Winzor, D. J., and Pielak, G. J. (2001) Annu. Rev. Biophys.
Biomol. Struct., 30, 271-306.
20.Minton, A. P. (2001) Biophys. J.,
80, 1641-1648.
21.Laurent, T. C. (1963) Biochem. J.,
89, 253-257.
22.Ross, P. D., and Minton, A. P. (1977) J. Mol.
Biol., 112, 437-452.
23.Minton, A. P., and Wilf, J. (1981)
Biochemistry, 20, 4821-4826.
24.Monod, J., Wyman, J., and Changeux, J. P. (1965)
J. Mol. Biol., 12, 88-118.
25.Minton, A. P. (1990) Int. J. Biochem.,
22, 1063-1067.
26.Ralston, G. B. (1990) J. Chem. Educ.,
67, 857-860.
27.Hall, D., and Minton, A. P. (2004) Biophys.
Chem., 107, 299-316.
28.Farruggia, B., Nerli, B., and Pico, G. (2003)
J. Chromatogr. B. Analyt. Technol. Biomed. Life Sci.,
798, 25-33.
29.Farruggia, B., Garcia, G., D'Angelo, C., and
Pico, G. (1997) Int. J. Biol. Macromol., 20, 43-51.
30.Tokuriki, N., Kinjo, M., Negi, S., Hoshino, M.,
Goto, Y., Urabe, I., and Yomo, T. (2004) Prot. Sci., 13,
125-133.
31.Sasahara, K., McPhie, P., and Minton, A. P.
(2003) J. Mol. Biol., 326, 1227-1237.
32.Minton, K. W., Karmin, P., Hahn, G. M., and
Minton, A. P. (1982) Proc. Natl. Acad. Sci. USA, 79,
7107-7111.
33.Rivas, G., Fernandez, J. A., and Minton, A. P.
(1999) Biochemistry, 38, 9379-9388.
34.Rivas, G., Fernandez, J. A., and Minton, A. P.
(2001) Proc. Natl. Acad. Sci. USA, 98, 3150-3155.
35.Wilf, J., and Minton, A. P. (1981) Biochim.
Biophys. Acta, 670, 316-322.
36.Torbert, J. (1986) Biochemistry,
25, 5309-5314.
37.Drenckhahn, D., and Pollard, T. D. (1986) J.
Biol. Chem., 261, 12754-12758.
38.Tellam, R. L., Sculley, M. J., and Nichol, L. W.
(1983) Biochem. J., 213, 651-659.
39.Bosma, H. J., Voordouw, G., de Kok, A., and
Veeger, C. (1980) FEBS Lett., 120, 179-182.
40.Zimmerman, S. B., and Trach, S. O. (1988)
Nucleic Acids Res., 16, 6309-6326.
41.Jarvis, T. C., Ring, D. M., Daube, S. S., and von
Hippel, P. H. (1990) J. Biol. Chem., 265,
15160-15167.
42.Kurganov, B. I., Topchieva, I. N., Lisovskaya, N.
P., Chebotareva, N. A., and Natarius, O. Ya. (1979) Biokhimiya,
44, 629-633.
43.Ren, G., Lin, Z., Tsou, C. L., and Wang, C. C.
(2003) J. Prot. Chem., 22, 431-439.
44.Sunshine, H. R., Hofrichter, J., and Eaton, W. A.
(1979) J. Mol. Biol., 133, 435-467.
45.Uversky, V., Cooper, M., Bower, K., Li, J., and
Fink, A. (2001) FEBS Lett., 515, 99-103.
46.Shtilerman, M. D., Ding, T. T., and Lansbury, P.
T., Jr. (2002) Biochemistry, 41, 3855-3860.
47.Hatters, D. M., Minton, A. P., and Howlett, G. J.
(2002) J. Biol. Chem., 277, 7824-7830.
48.Kozer, N., and Schreiber, G. (2004) J. Mol.
Biol., 336, 763-774.
49.Harding, S. E., Rowe, A. J., and Horton, J. C.
(eds.) (1992) Analytical Ultracentrifugation in Biochemistry and
Polymer Science, Royal Society of Chemistry, Cambridge.
50.Rivas, G., and Minton, A. P. (2003) Biochem.
Soc. Trans., 31, 1015-1019.
51.Eggers, D. K., and Valentine, J. V. (2001) J.
Mol. Biol., 314, 911-922.
52.Caspar, D. L. D., and Klug, A. (1962) Cold
Spring Harbor Symp., 27, 1-24.
53.Anfinsen, C. B. (1973) Science,
181, 223-230.
54.Ellis, R. J. (1987) Nature, 328,
378-379.
55.Ellis, R. J., and Hemmingsen, S. M. (1989)
Trends Biochem. Sci., 14, 339-342.
56.Hartl, F. U., and Hayer-Hartl, M. (2002)
Science, 295, 1852-1858.
57.Markossian, K. A., and Kurganov, B. I. (2004)
Biochemistry (Moscow), 69, 971-984.
58.Agashe, V. R., and Hartle, F.-U. (2000) Semin.
Cell Dev. Biol., 11, 15-25.
59.Sigler, P. B., Xu, Z., Rye, H. S., Burston, S.
G., Fenton, W. A., and Horwich, A. L. (1998) Annu. Rev.
Biochem., 67, 581-608.
60.Gottesman, M. E., and Hendrickson, W. A. (2000)
Curr. Opin. Microbiol., 3, 197-202.
61.Ellis, R. J. (1997) Curr. Biol., 7,
R531-R533.
62.Martin, J. (2002) Biochemistry, 41,
5050-5055.
63.Van den Berg, B., Wain R., Dobson, C. M., and
Ellis, R. J. (2000) EMBO J., 19, 3870-3875.
64.Yancey, P. H., and Somero, G. N. (1979)
Biochem. J., 183, 317-323.
65.Yancey, P. H., Clark, M. E., Hand, S. C., Bowlus,
R. D., and Somero, G. N. (1982) Science, 217,
1214-1222.
66.Wang, A., and Bolen, D. W. (1997)
Biochemistry, 36, 9101-9108.
67.Bolen, D. W., and Baskakov, I. V. (2001) J.
Mol. Biol., 310, 955-963.
68.Burg, M. B., and Peters, E. M. (1997) Am. J.
Physiol., 273, F1048-F1053.
69.Baskakov, I. V., and Bolen, D. W. (1998)
Biophys. J., 74, 2658-2665.
70.Baskakov, I. V., and Bolen, D. W. (1998) J.
Biol. Chem., 273, 4831-4834.
71.Liu, Y., and Bolen, D. W. (1995)
Biochemistry, 34, 12884-12891.
72.Mashino, T., and Fridovich, I. (1987) Arch.
Biochem. Biophys., 258, 356-360.
73.Meng, F.-G., Park, Y.-D., and Zhou, H.-M. (2001)
Int. J. Biochem. Cell Biol., 33, 701-709.
74.Satoro, M. M., Liu, Y., Khan, S. M. A., Hou,
L.-X., and Bolen, D. W. (1992) Biochemistry, 31,
5278-5283.
75.Yancey, P. H., and Somero, G. N. (1980) J.
Exp. Zool., 212, 205-213.
76.Zou, Q., Bennion, B. J., Daggett, V., and Murphy,
K. P. (2002) J. Am. Chem. Soc., 124, 1192-1202.
77.Shearwin, K. E., and Winzor, D. J. (1988)
Biophys. Chem., 31, 287-294.
78.Cann, J. R., Coombs, R. O., Howlett, G. R.,
Jacobsen, M. P., and Winzor, D. J. (1994) Biochemistry,
33, 10185-10190.
79.Chebotareva, N. A., Harding, S. E., and Winzor,
D. J. (2001) Eur. J. Biochem., 268, 506-513.
80.Chebotareva, N. A., Andreeva, I. E., Makeeva, V.
F., Kurganov, B. I., Livanova, N. B., and Harding, S. E. (2002)
Progr. Colloid. Polym. Sci., 119, 70-76.
81.Carner, M. R., and Rau, D. C. (1995) EMBO
J., 14, 1257-1263.
82.Poon, J., Bailey, M., Winzor, D. J., Davidson, B.
E., and Sawyer, W. H. (1997) Biophys. J., 73,
3257-3264.
83.Patel, C. N., Noble, S. M., Weatherly, G. T.,
Tripathy, A., Winzor, D. J., and Pielak, G. J. (2002) Prot.
Sci., 11, 997-1003.
84.Wills, P. R., Jacobsen, M. P., and Winzor, D. J.
(1996) Biopolymers, 38, 119-130.
85.Ogston, A. G., and Winzor, D. J. (1975) J.
Phys. Chem., 79, 2496-2500.
86.Nichol, L. W., Jeffrey, P. D., and Winzor, D. J.
(1976) J. Phys. Chem., 80, 648-649.
87.Meng, F.-G., Hong, Y.-K., He, H.-W., Lyubarev, A.
E., Kurganov, B. I., Yan, Y.-B., and Zhou, H.-M. (2004) Biophys.
J., 87, 2247-2254.
88.Morar, A. S., Olteanu, A., Young, G. B., and
Pielak, G. J. (2001) Prot. Sci., 10, 2195-2199.
89.Saunders, A. J., Davis-Searles, P. R., Allen, D.
L., Pielak, G. J., and Erie, D. A. (2000) Biopolymers,
53, 293-307.
90.Lonhienne, T. G. A., and Winzor, D. J. (2001)
Biochemistry, 40, 9618-9622.
91.Lonhienne, T. G. A., and Winzor, D. J. (2002)
Biochemistry, 41, 6897-6901.
92.Koshland, D. E., Nemethy, G., and Filmer, D.
(1966) Biochemistry, 5, 365-385.
93.Weatherly, G. T., and Pielak, G. J. (2001)
Prot. Sci., 10, 12-16.
94.Jacobsen, M. P., Wills, P. R., and Winzor, D. J.
(1996) Biochemistry, 35, 13173-13179.
95.Hall, D. R., Jacobsen, M. P., and Winzor, D. J.
(1995) Biophys. Chem., 57, 47-54.
96.Wills, P. R., Hall, D. R., and Winzor, D. J.
(2000) Biophys. Chem., 84, 217-225.
97.Timasheff, S. N. (1992) Biochemistry,
31, 9857-9864.
98.Timasheff, S. N. (1993) Annu. Rev. Biophys.
Biochem. Struct., 22, 67-97.
99.Arakawa, T., Bhat, R., and Timasheff, S. N.
(1985) Biophys. J., 47, 411-414.
100.Baskakov, I. V., and Bolen, D. W. (1998)
Biophys. J., 74, 2666-2673.
101.Qu, Y., Bolen, C. L., and Bolen, D. W. (1998)
Proc. Natl. Acad. Sci. USA, 95, 9268-9279.
102.Palmer, H. R., Bedford, J. J., Leader, J. P.,
and Smith, R. A. J. (2000) J. Biol. Chem., 36,
27708-27711.
103.Lee, J. C., Gekko, K., and Timashev, S. N.
(1979) Meth. Enzymol., 61, 26-49.
104.Sackett, D. L. (1997) Am. J. Physiol.,
273, R669-R676.
105.Yang, D.-S., Yip, C. M., Huang, T. H. J., and
Chakrabatty, A. (1999) J. Biol. Chem., 274,
32970-32974.