Simulation of DNA Bases in Water: Comparison of the Monte Carlo Algorithm with Molecular Mechanics Force Fields
M. Monajjemi1*, S. Ketabi2, M. Hashemian Zadeh3, and A. Amiri4
1Department of Chemistry, Science and Research Campus, Islamic Azad University, P.O. Box 14155-775, Tehran, Iran; E-mail: m_monajjemi@yahoo.com2Department of Chemistry, Central Tehran Campus (East Tehran-Ghiam Dasht), Islamic Azad University, Tehran, Iran
3Department of Chemistry, University of Science and Technology of Iran, Tehran, Iran
4Department of Chemistry, Central Tehran Campus, Islamic Azad University, Tehran, Iran
* To whom correspondence should be addressed.
Received September 1, 2004
The interaction between the nucleic acid bases and solvent molecules has an important effect in various biochemical processes. We have calculated total energy and free energy of the solvation of DNA bases in water by Monte Carlo simulation. Adenine, guanine, cytosine, and thymine were first optimized in the gas phase and then placed in a cubic box of water. We have used the TIP3 model for water and OPLS for the nucleic acid bases. The canonical (T, V, N) ensemble at 25°C and Metropolis sampling technique have been used. Good agreement with other available computational data was obtained. Radial distribution functions of water around each site of adenine, guanine, cytosine, and thymine have been computed and the results have shown the ability of the sites for hydrogen bonding and other interactions. The computations have shown that guanine has the highest value of solvation free energy and N7 and N6 in adenine and guanine, N3 in cytosine, and N3 and O4 in thymine have the largest radial distribution function. Monte Carlo simulation has also been performed using the CHARMM program under the same conditions, and the results of two procedures are compared.
KEY WORDS: Monte Carlo simulation, radial distribution function, force field, hydration, adenine, guanine, cytosine, thymineDOI: 10.1134/S0006297906130013
The hydration of biomolecules is vitally important in molecular biology since numerous biological processes involve a ligand binding to a nucleic acid or protein and thereby displacing the water hydration. Unfortunately, a biomolecule-water potential energy surface cannot be constructed from accurate ab initio calculations, even with recent growth in computer power, because too many points are required. For example, we have studied the interaction of metal ions with DNA bases in the gas phase and different solvent [1, 2], but we used the Polarized Continuum Model for the solution phase, and we could not use all of the solvent molecules in ab initio calculations. Clearly, the construction of a potential energy surface for such large systems, using more elaborate ab initio techniques, is currently not feasible. Thus it is suitable to use computer simulation methods for these systems.
The ability to accurately calculate solvation energies of molecules using molecular simulation methods is an important development in computational chemistry. These methods have wide applicability not only in studies of solvation free energies, but also in studies of binding free energies and protein and nucleic acid stability. Early works in this area focused on small, nonpolar molecules [3], but more work has involved investigations of polar molecules [4, 5] including systems where polarization effects are thought to be significant [6]. While it is important that these methods reproduce the experimental results, the real aim is to use these theoretical methods in a predictive manner in cases where experiments cannot be performed.
Knowledge of solvation free energies of DNA bases would be useful, for example, in understanding the forces involved in protein-nucleic acid interactions and the stability of nucleic acid tertiary structures. In this case, the application of theoretical models may be our best hope to gain physical insights in to the effects of solvation. This has been recognized for some time, and different theoretical models have been used to compute these solvation energies [7-13]. It is discouraging, however, that the various methods sometimes give very different results, bringing into question the applicability and accuracy of the models themselves.
In this paper, we present quantitative results of Monte Carlo calculations of solvation energies of adenine, guanine, cytosine, and thymine in water. We have used quantum mechanical calculations for isolated solute molecules and then applied Monte Carlo (MC) simulation for dilute solutions of DNA bases in water. We have done the MC simulation with two procedures. We have written a FORTRAN program for the system of DNA bases in water and then calculated the solvation energy of the system using the program. We also have used the CHARMM [14, 15] program for MC simulation of these DNA bases in water. The conclusions drawn from these calculations are then contrasted and compared.
METHODS OF INVESTIGATION
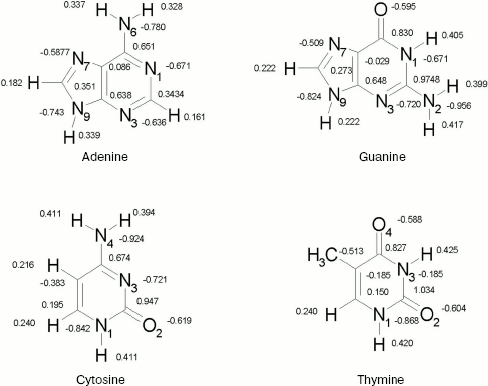
Geometries. For nucleic acid bases, geometries were optimized by ab initio calculations using the standard 6-31+G* basis set [16]. Each base has been optimized in Hartree-Fock level. The calculations have been performed by using the GAUSSIAN 98 suite of programs [17]. The resultant structures are shown in Fig. 1. We show only partial atomic charges since in further calculations the charges have been used. In all subsequent calculations, these geometries were kept constant.
Potential energy functions. The key factor in determining the accuracy of computer simulations is the quality of intermolecular potential functions. These functions are obtained either by empirical methods or from quantum-mechanical calculations, the latter method being used in most of the recent simulations of fluids. The intermolecular potential functions are described in detail elsewhere [18-22].Fig. 1. DNA bases.
Total potential energy of a chemical system, Etot, includes internal potential energy (Eint) and external potential energy (Eext) terms:
Etot = Eint + Eext. (1)
In our program, internal potential function has been disregarded and only external or intermolecular potential function has been considered.
The monomers are represented by interaction sites usually located on nuclei. The interaction energy between two molecules, a and b, were expressed by the pair wise sum of interaction contributions:
We have used Transferable Intermolecular Potential functions [18, 21] (TIP3) for water molecules (solvent) and Optimized Potential for Liquid Simulations [22] (OPLS) for adenine, guanine, cytosine, and thymine in solution. For both models, the pair potential function Eij was represented by Columbic and Lennard-Jones terms between sites centered on nuclei (Eq. (3)):
As indicated in Eq. (3), each type of site has three parameters, a charge in electron, q, and A and C. The TIP3 model uses a total of the three sites for the electrostatic interactions. The partial positive charges on the hydrogen atoms are exactly balanced by an appropriate negative charge located on the oxygen atom. The TIP3 parameters for water [19] have been included in Table 1.
The OPLS model is a modified form of TIPS that has parameters fitted to liquid state properties, and so is more suitable for studies of liquids. The model works well for a variety of alcohols, amines, aliphatic and aromatic hydrocarbons, sulfur compounds, ether, amino acids, and nucleic acid bases. It has the form of Eq. (3). The Lennard-Jones parameters between pairs of different atoms are obtained from the Lorentz-Berthelodt combination rules:
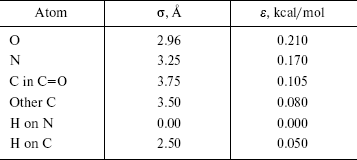
The OPLS Lennard-Jones parameters for nucleic acid bases [22] are included in Table 2. We have used quantum mechanical calculated partial charges that are shown in Fig. 1.
Table 1. TIP3 parameters for water

Table 2. OPLS Lennard-Jones parameters for
nucleic acid bases
In the second section of our research, calculations were performed with the simulation program CHARMM [14, 15], in which an empirical energy function that contains terms of both internal and external interactions was used. The internal energy function has the form:
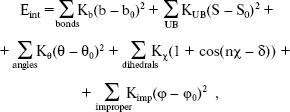 (8)
(8)
where Kb, KUB, Ktheta, Kchi, and Kimp are the bond, Urey-Bradley, angle, dihedral angle, and improper dihedral angle force constants, respectively; b, S, theta, chi, and phi are bond length, Urey-Bradley 1,3-distance, bond angle, dihedral angle, and improper torsion angle, respectively, with the subscript zero representing the equilibrium values for the individual terms.
Monte Carlo procedure. Monte Carlo statistical mechanical simulations were carried out in standard manner using the Metropolis sampling technique [23] in canonical (T, V, N) ensemble. All calculations were performed in a cubic box at experimental density of water, 1 g/cm3. The edges of the box were 22 × 22 × 22 Å, which corresponds to 352 H2O molecules of pure solvent. A spherical cut off for the potential at an OO separation of half the length of an edge of the cube was used. One molecule was picked and displaced randomly on each move. An acceptance rate of 50% for new configurations was achieved by using ranges of ±0.12 Å for the translations and ±15° for the rotation about a randomly chosen axis. Periodic boundary conditions were employed in computation of energy of the initial configuration, in cut off, in translations and rotations, and computation of the energy of each produced configuration. The system was thoroughly equilibrated using several hundred thousand configurations. The energy of a configuration was obtained from the pair wise sum of the dimerization energies for each monomer as usual.
Each run consisted of 106 attempted moves. Initial steps (roughly 5*105) were disregarded for equilibrium. Every calculation was extended to include as many configurations as were necessary to reduce the statistical error to the level at which calculated energy differences have quantitative significance.
In the CHARMM calculations, we used adenine residue in a cubic box image of water. The edge of the cubic box is 22 Å like before. The translation and the rotation and the number of steps have been considered the same as in previous work.
RESULTS AND DISCUSSION
Total energies. The interaction between the solute and the solvent molecules plays a crucial role in understanding the various molecular processes involved in chemistry and biochemistry.
It is established from various experimental and theoretical methods that water plays a definite role in the stacking of DNA bases [24]. In this study, we have analyzed the solvation of the DNA bases (adenine, guanine, thymine, and cytosine) in the presence of water. We have used very dilute solution of DNA bases, so one molecule of adenine, guanine, cytosine, and thymine has merged in water and then average energies were calculated from Monte Carlo (MC) simulations. The resultant configuration of the MC simulation of adenine in water is shown in Fig. 2. This gives a qualitative idea of the formation of the solvation shell around the selected DNA bases. The total energy of the bases (including van der Waals and Coulomb interaction) in water has been calculated. The average energy (Etot) calculated from MC simulations, as well as the energies of solute-solvent (Esoln) and solvent-solvent (Esolv) components, are given in Table 3. This table also includes the number of solvent molecules (N), the total number of MC steps (NSTEP), and the actual number of configurations (NSTEPav) used in calculating ensemble averages for every run.
Calculated energy values, as well as various structural parameters, can be further used to analyze solvation energies of the nucleic acid bases. The process of solvation of the solute molecule (Base) in water is:
Base (g) <--> Base (aq). (9)
The DeltaEtot term can be represented as the sum of the energy contributions from solute-solvent (DeltaEsoln), solvent-solvent (DeltaEsolv), and intramolecular (DeltaEint) interactions:
DeltaEtot = DeltaEsoln + DeltaEsolv + DeltaEint. (10)
Since the positions of atoms in the solute molecule are have been kept fixed, DeltaEint remains constant through the Monte Carlo process.
The results shown in the last column of Table 3 indicate that the stability of DNA bases in water are guanine > thymine > cytosine > adenine. It is known that polar molecules are soluble in polar solvent and non-polar molecules dissolve readily in non-polar solvent systems. In our calculations as well, we observe that the less polar DNA bases exhibit less solubility in the water.
Table 3. Summary of Monte Carlo runs

Note: Esoln, Esolv, and Etotal are in
kcal/mol.
In our calculations using the CHARMM program, we have placed an adenine residue in water and then optimized the system using the program. The functions and the parameters [25] that are implemented in CHARMM were used.
The Etot with NSTEP = 98,035 is -35.2383 kcal/mol by CHARMM. That has been averaged over 46,169 configurations. With 1,000,000 configurations the Etot was -35.3429 over 373,399 configuration average.
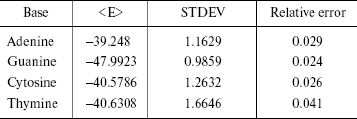
Error estimation. A simulation can generate an enormous amount of data that should be properly analyzed to extract relevant properties and to check that the calculation has behaved properly. The three most important factors that determine the accuracy of Monte Carlo calculations are the quality of intermolecular potentials, the sample-size effect, and statistical fluctuations of calculated ensemble averages. The first was briefly discussed. The second factor arises because locating a limit number of molecules in a box followed by subsequent application of periodic boundary conditions introduces an error into the molecular correlations. For a given system, this effect decreases with the sample size. In most cases of interest, we do not know how to choose the size of the system in order to minimize an effect of periodic boundary conditions. The most straightforward test is to perform a series of calculations in which the sample size is systematically increased until calculated values remain unchanged.Fig. 2. Final configuration of adenine-water.
The statistical errors are often reported as standard deviations. The errors have been reported in Table 4. STDEV is the standard deviation of the calculated average in the simulation of finite number of steps. As shown in Table 4, the simulation error is 2-4%.
Table 4. Simulation errors
Free energies. The free energy differences between two states 1 and 2 of a system can be derived from classical statistical mechanics [26] allowing us to express this function as:
Here, (E2 - E1) is the potential energy differences (DeltaA) between states 1 and 2 of the system, R is the molar gas constant, T is absolute temperature, and the symbol < > indicates an ensemble average. Since the isothermal-isobaric ensemble has been used, Gibbs free energies have the same expression. The computed free energies are presented in Table 5. The table also has the result of other authors and other methods as well as semiempirical [9, 28, 29], ab initio [7, 28], combined quantum mechanical and molecular mechanical methods (QM/MM) [13], and finite difference Poisson-Boltzmann (FDPB) models [10]. It should be noted that except for our work and the QM/MM method, the values are for methylated DNA bases. Methylation decreases the hydration free energy of the bases [9].
Table 5. Computed solvation free
energies
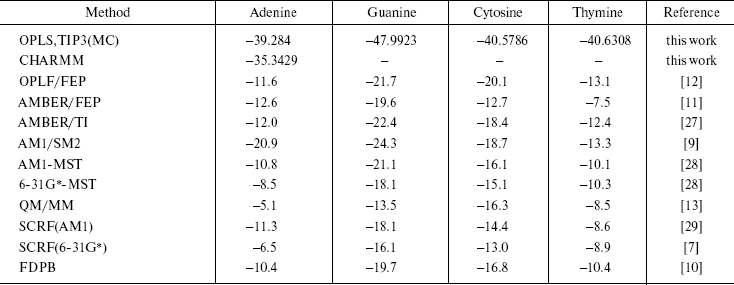
The results of our work show that guanine is the most stable DNA base in water. The other methods have also given this conclusion. Of course, their results are different numerically, but the approach of the data is the same. The differences are due to many reasons. The usage of force field by the methods is different. We use only intermolecular potential function that has Columbic and Lennard-Jones terms, and do not consider internal coordinate, while in AMBER and CHARMM force field total potential energy is the sum of the bond stretching, angle bending torsional terms plus Columbic and Lennard-Jones terms. The goal of each simulation procedure is simplicity of the system together with quality of results. We have obtained similar results by the simpler force field. For monomers (solute and solvent molecules), the geometries during the simulations were kept fixed so intramolecular vibrational effects have not been considered. This simplicity is correct for small molecules and reduces the time required for calculations. The results of our CHARMM computations confirm this conclusion.
Another reason for the differences in the results are differences in box size and cut off. Also, in SCRF (Self-Consistent Reaction Field method) and other quantum mechanical procedures, the solvent is viewed as a continuous medium of uniform dielectric constant.
The results of the AMBER method are closer to the semiempirical results of both Orozco and Cramer than they are to the results from any of the ab initio methods.
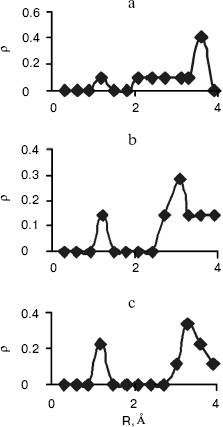
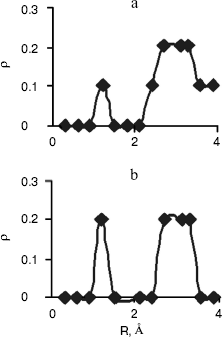
Radial Distribution Functions (RDFS). Radial distribution functions between water molecules and each site of the solute molecule are important in hydrogen bonding and interaction of that site with ions. So we have computed radial distribution functions between water molecules and N1, N3, N7, and N6 atoms of adenine, N1, N3, N7, and O6 atoms of guanine, N3, N4, and O2 atoms of cytosine, and N1, N3, O2, and O4 atoms of thymine. We have computed RDFS under 4 Å, since the R greater than 4 Å is related to hydrogen bonding of water molecules with each other. The results are reported in Table 6. Under 4 Å, there are two coordination layers of water molecules around each site. rho1 is the first coordination layer that is located at the distance r1, and rho2 is the second coordination layer that is located at the distance r2. Figures 3 and 4 show RDFS for some the sites of the DNA bases. All of the RDFS diagrams have two peaks that are related to the first and second solvent shells. As shown, the first peak of all sites and bases occurs at 1.2 Å and is a sharp peak. N6 and N7 in adenine, O6 in guanine, N4 in cytosine, and N3 in thymine have the highest first peak. For all the DNA bases, the second coordination shell occurs at about 3 Å. Table 6 reveals that the highest second peak for adenine and guanine is related to N7 that is centered at 3.30 and 3.00 Å, respectively. For cytosine and thymine, the highest second band can be assigned to water molecules around N3 and N1 and is located at 3.15 and 3.3 Å, respectively. These results reveal that N7 and N6 in adenine and guanine, N3 in cytosine, and N3 and O4 in thymine are the most hydrophilic atoms in each base. It means that these sites are the most active atoms in these molecules and have the potential for taking part in hydrogen bonding or interaction with metal ions. These results are in good agreement with the experimental data since the Watson-Crick model for hydrogen bonding between the bases proposed the interaction of the N6 and N7 of adenine and O4 and N3 of thymine. Also, the experimental results show that the best site for protonation of adenine and guanine is N7, for cytosine is N3, and for thymine is N1 or N3 [30].
Table 6. RDFS between different sites of DNA
bases and water
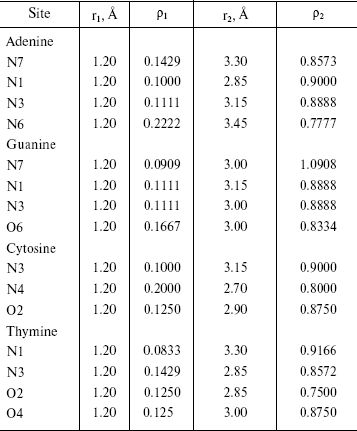
Fig. 3. Computed radial distributions between water and N1 (a), N7 (b), and N6 (c) atoms of adenine.
Fig. 4. Computed radial distributions between water and N3 (a) and N4 (b) atoms of cytosine.
CONCLUSION
In this research study, we calculated solvation free energy for the nucleic acid bases. These energies are unattainable experimentally because of the lack of volatility of the bases. Our computation shows that guanine is the most stable DNA base in water. Adenine has the minimum value of the solvation free energy and guanine has the maximum value of the solvation free energy. Our work is comparable with CHARMM and other computational methods.
We have also computed radial distribution function between the active sites in the DNA bases and water molecules. Our computation has shown that N7 and N6 in adenine and guanine, N3 in cytosine, and N3 and O4 in thymine are the most active sites for the interaction of these bases with hydrogen of water and with other positive sites. These results determine the best site of hydrogen bonding between DNA bases that are compatible with the Watson-Crick model.
REFERENCES
1.Monajjemi, M., Ghiasi, R., Ketabi, S., Pasdar, H.,
and Mollaamin, F. (2004) J. Chem. Res., January, 11-18.
2.Monajjemi, M., Ghiasi, R.,s Ketabi, S., Pasdar, H.,
Mollaamin, F., Asaddian, F., Chahkandi, B., and Karimkhani, M. (2003)
Int. Elec. J. Mol. Des., 2, 11, 741-756.
3.Jorgensen, W. L., and Ravimohan, C. J. (1985) J.
Chem. Phys., 83, 3050-3054.
4.Sun, Y. X., Spellmeyer, D., Pearlman, D. A., and
Kollman, P. A. (1992) J. Am. Chem. Soc., 114,
6798-6801.
5.Cornell, W. D., Cieplak, P., Bayly, C. I., and
Kollman, P. A. (1993) J. Am. Chem. Soc., 115,
9620-9631.
6.Morgantini, P. Y., and Kollman, P. A. (1995) J.
Am. Chem. Soc., 117, 6057-6063.
7.Young, P. E., and Hillier, I. J. (1993)
Chem. Phys. Lett., 215, 405-408.
8.Orozco, M., and Luque, F. J. (1993)
Biopolymers, 33, 1851-1870.
9.Cramer, C. J., and Truhlar, D. G. (1992) Chem.
Phys. Lett., 198, 74-80.
10.Mohan, V., Davis, M. E., McCammon, J. A., and
Pettitt, B. M. (1992) J. Phys. Chem., 96, 6428-6431.
11.Bash, P. A., Singh, U. C., Langridge, R., and
Kollman, P. A. (1987) Science, 236, 564-568.
12.Elcock, A. H., and Richards, W. G. (1993) J.
Am. Chem. Soc., 115, 7930-7931.
13.Gao, J. L. (1994) Biophys. Chem.,
51, 253-261.
14.Brooks, B. R., Bruccoleri, R. E., Olafson, B. D.,
States, D. J., Swainethan, S., and Karplus, M. (1983) J. Comput.
Chem., 4, 187-217.
15.CHARMM (Chemistry at Harvard Macromolecular
Mechanics) software, Department of Chemistry & Chemical Biology,
Harvard University, Cambridge.
16.Clark, T., Chandrasekhar, J., Spitznagel, G. W.,
and Schleger, P. V. R. (1983) J. Comp. Chem., 4,
294-301.
17.Frisch, M. J., Trucks, G. W., Schlegel, B. H.,
Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Zakrzewski, V. G.,
Montgomery, J. A., Stratmann, R. E., Burant, J. C., Dapprich, S.,
Millam, J. M., Daniels, A. D., Kudin, K. N., Strain, M. C., Farkas, O.,
Tomasi, J., Barone, V., Cossi, M., Cammi, R., Mennucci, B.,
Pomelli, C., Adamo, C., Clifford, S., Ochterski, J., Petersson, G. A.,
Ayala, P. Y., Cui, Q., Morokuma, K., Malick, D. K., Rabuck, A. D.,
Raghavachari, K., Foresman, J. B., Cioslowski, J., Ortiz, J. V.,
Stefanov, B. B., Liu, G., Liashenko, A., Piskorz, P., Komaromi, I.,
Gomperts, R., Martin, R. L., Fox, D. J., Keith, T., Al-Laham, M. A.,
Peng, C. Y., Nanayakkara, A., Gonzalez, C., Challacombe, M., Gill,
P. M. W., Johnson, B., Chen, W., Wong, M. W., Andres, J. L.,
Gonzalez, C., Head-Gordon, M., Replogle, E. S., and Pople, J. A.
(1998) Gaussian 98, Revision A.7, Gaussian, Inc., Pittsburgh.
18.Jorgansen, W. L., Chandrasekhar, J., Madura, J.
D., Impey, R. W., and Klein, M. L. (1983) J. Chem. Phys.,
79, 926-935.
19.Jorgansen, W., and Sswenson, C. J. (1985)
J. Am. Chem. Soc., 107, 1489-1496.
20.Jorgansen, W., and Madura, J. C. (1984) J. Am.
Chem. Soc., 106, 6638-6646.
21.Jorgansen, W. L. (1981) J. Am. Chem. Soc.,
103, 335-340.
22.Pranata, J., Wierschke, S. G., and Jorgansen, W.
L. (1991) J. Am. Chem. Soc., 113, 2810-2819.
23.Metropolis, N., Rosenbulth, A. W., Rosenbulth, M.
N., Teller, A. H., and Teller, E. (1953) J. Chem. Phys.,
21, 1087-1092.
24.Saenger, W. (1984) Principles of Nucleic Acid
Structure, Springer, New York.
25.MacKerell, A. D., Jr., Wiokiewicz-Kuczera, J.,
and Karplus, M. (1995) J. Am. Chem. Soc., 117,
11946-11975.
26.Beveridge, D. L., and Di Cupua, F. M. (1989)
Annu. Rev. Biophys. Chem., 18, 431-492.
27.Miller, J. L., and Kollman, P. A. (1996) J.
Phys. Chem., 100, 8587-8594.
28.Orozco, M., Colominas, C., and Luque, F. J.
(2006), in preparation.
29.Orozco, M., and Luque, F. J. (1993)
Biopolymer, 33, 1851-1869.
30.Izatt, R. M., Christensen, J. J., and Rytting, J.
H. (1971) Chem. Rev., 71, 5 439-481.