Quasi-Equilibrium Assumption for Arbitrary Mechanism of Enzymatic Reaction. Criteria for Existence of Equilibrium Segments

---

P. V. Vrzheshch^1,2

¹Department of Bioengineering and Bioinformatics, Lomonosov Moscow State University, 119992 Moscow, Russia; fax: (495) 939-4218; E-mail: peter@genebee.msu.ru

²International Biotechnological Center, Lomonosov Moscow State University, 119992 Moscow, Russia; fax: (495) 939-5022

Received September 26, 2010; Revision received December 8, 2010

---

The possible application of the quasi-equilibrium assumption for an arbitrary mechanism of enzymatic reaction is considered. It is shown at what ratios of kinetic constants a segment consisting of two, three, and four intermediates may be considered as an equilibrium one. Expressions for evaluation of accuracy of distribution of intermediate concentrations inside the equilibrium segment and accuracy of determination of intermediate concentrations inside and outside the equilibrium segment as a function of the ratio of kinetic constants are derived. A method for determination of the limitations on the ratio of rate constants for an equilibrium segment of arbitrary structure is suggested.

---

KEY WORDS: enzyme kinetics, quasi-equilibrium assumption, accuracy of assumption, Cha method, rapid equilibrium, steady-state kinetics, graph method

DOI: 10.1134/S0006297911040134

Successful application of the quasi-equilibrium assumption for steady-state schemes of enzymatic reactions crucially depends on a proper choice of the equilibrium segment. The Cha method [1] of calculation of schemes of enzymatic reactions under the conditions of the quasi-equilibrium assumption is not proved in a general case, general criteria for existence of equilibrium segments are absent, and this raises discussions on the subject and doubts of correctness of the Cha method and in applicability of the quasi-equilibrium assumption at all [2-6]. Incorrect application of this assumption is shown to cause serious errors [7, 8].

If intermediates X_A and X_B are considered as the equilibrium segment in an arbitrary enzymatic reaction mechanism (1), the quasi-equilibrium assumption of mechanism (1) corresponds to the quasi-equilibrium mechanism (2); intermediate Y designates intermediates X_A and X_B taken at a ratio corresponding to a state of true equilibrium between them.

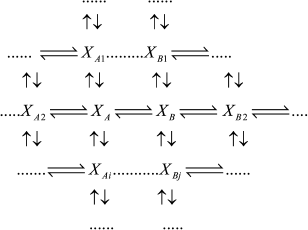    (1)

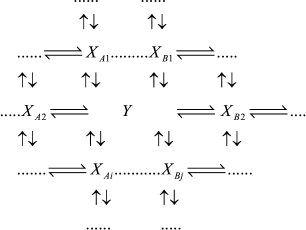    (2)

In accord with the Cha method [1], each rate constant for reaction Y →X_Ai in mechanism (2) is equal to

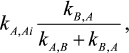
and each rate constant for reaction Y→X_Bi in mechanism (2) is equal to

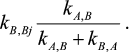
All other rate constants in mechanism (2) are equal to the corresponding rate constants in mechanism (1).

In this work it is shown that accuracy of the quasi-equilibrium assumption depends on the ratio of rate constants of reactions outside the equilibrium segment and rate constants inside this segment: the lesser this ratio the higher is the accuracy of the quasi-equilibrium assumption. For mechanism (1), under condition

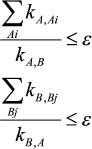    (3)

the ratios of values in the steady-state assumption (upper index ss), quasi-equilibrium assumption (upper index qe), and in the equilibrium state (upper index eq) are as follows:

    (4)

    (5)

where X_m is an arbitrary intermediate.

In a case when three intermediates of mechanism (1), X_A, X_B, and X_C, are considered as an equilibrium segment, conditions for the quasi-equilibrium assumption and its accuracy look as follows:

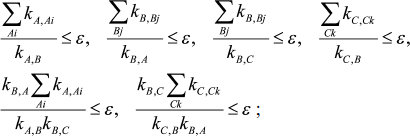    (6)

    (7)

Analogous ratios were obtained for equilibrium segments consisting of four intermediates (open and closed segments) and the algorithm for evaluation of accuracy of the quasi-equilibrium assumption in a case of arbitrary equilibrium segment (see Supporting information for the paper on the site of Biochemistry (Moscow) (http://protein.bio.msu.ru/biokhimiya)). Exact proofs for the above mentioned statements are also given there.

This work was financially supported by the Russian Foundation for Basic Research (grant No. 09-04-01511-a) and the Federal Agency for Science and Innovations (state contract No. 02.740.11.0291 (July 7, 2009) in the framework of the program “Scientific and Scientific-Pedagogical Personnel of Innovational Russia for 2009-2013”, enterprise 1.1).

REFERENCES

1.Cha, S. (1968) J. Biol. Chem., 243, 820-825.
2.Varon, R., Garcia-Moreno, M., Garrido, C., and Garcia-Canovas, F. (1992) Biochem. J., 288, 1072-1073.
3.Segel, I. H., and Martin, R. L. (1988) J. Theor. Biol., 135, 445-453.
4.Topham, C. M., and Brocklehurst, K. (1992) Biochem. J., 282, 261-265.
5.Selwyn, M. J. (1993) Biochem. J., 295, 897-898.
6.Brocklehurst, K., and Topham, C. M. (1993) Biochem. J., 295, 897-898.
7.Vrzheshch, P. V. (2008) Biochemistry (Moscow), 73, 1114-1120.
8.Vrzheshch, P. V. (2010) Biochemistry (Moscow), 75, 1374-1382.

SUPPLEMENT

Supporting Information (PDF)

---