REVIEW: Energetic and Regulatory Role of Proton Potential in Chloroplasts
A. N. Tikhonov
Faculty of Physics, Lomonosov Moscow State University, 119991 Moscow, Russia; fax: (495) 932-8820; E-mail: an_tikhonov@mail.ru
Received April 8, 2012
The review focuses on the energetic and regulatory role of proton potential in the activity of chloroplasts, the light energy-converting organelles of plant cells. Mechanisms of generation of the transmembrane difference of electrochemical potentials of hydrogen ions (Δµ~H+) in the chloroplast thylakoid membranes are considered. Methods for measuring the intrathylakoid pH in chloroplasts are described. It is shown that under conditions of phosphorylation in chloroplasts, the pH of the intrathylakoid space decreases moderately (pHin ≥ 6.0-6.2, at the stroma pHout ≈ 7.8-8.0), with a corresponding concentration component of Δµ~H+ equal to ΔpH ≤ 1.6-2.0. On analyzing the energy and structural features of ATP synthase of chloroplasts, we conclude that the energy stored as the concentration component of the proton potential ΔpH is sufficient to sustain ATP synthesis. The mechanisms of pH-dependent regulation of electron transport in chloroplasts (photosynthetic control of electron transport, enhancement of non-photochemical quenching of chlorophyll excitation in the light-harvesting antenna, light-induced activation of the Calvin–Benson cycle reactions, activation of ATP synthase) are considered briefly.
KEY WORDS: bioenergetics, chloroplasts, proton potential, regulation of photosynthesisDOI: 10.1134/S0006297912090027
Abbreviations: ETC, electron transport chain; NPQ, non-photochemical quenching; PS1 and PS2, photosystems 1 and 2, respectively; TA, 4-amino-2,2,6,6-tetramethylpiperidine-1-oxyl.
The transmembrane difference of electrochemical potentials of hydrogen
ions (Δµ~H+) is one of the most
important characteristics of energy-converting systems of the cell [1-10]. The fundamental principle
of membrane bioenergetics states that
Δµ~H+ is one of the basic forms of
energy storage in the cell, which serves the driving force for the
energy-accepting reaction of ATP synthesis from ADP and Pi
catalyzed by proton ATP synthases of the FoF1
type. In chloroplasts, which are the light energy-converting organelles
of plant cells, Δµ~H+ is generated
due to the activity of the photosynthetic electron transport chain
(ETC). Electron transfer in the ETC is associated with accumulation of
protons inside the thylakoids, which results in a decrease in pH of the
intrathylakoid space (pHin↓). In the stroma, i.e. on
the outer side of the thylakoid membrane, protons are taken up, which
results in an increase in pH (pHout↑). According to the
chemiosmotic theory of energy coupling [1, 2], the proton flow through ATP synthase due to
Δµ~H+ sustains ATP synthesis:
ADP + Pi + nH+in ↔ ATP + H2O + nH+out. (1)
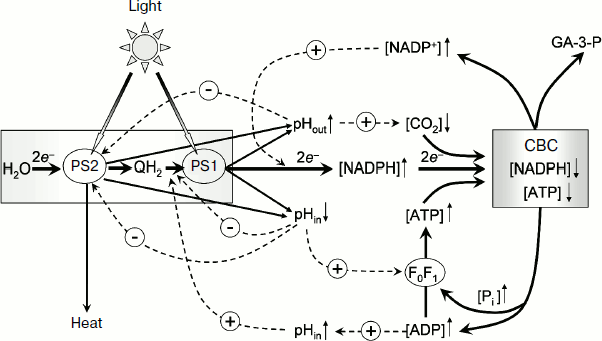
Moreover, Δµ~H+ regulates the rate of electron transfer in the ETC of chloroplasts. Acidification of the intrathylakoid space inhibits the electron transfer in the cytochrome section of the ETC between photosystem 2 (PS2) and photosystem 1 (PS1) [6, 11-15] and in a decrease in the photochemical activity of PS2 due to enhancement of thermal dissipation of energy in the light-harvesting antenna of PS2 (non-photochemical quenching of excitation of chlorophyll molecules [16-19]). Alkalization of the stroma activates the Calvin–Benson cycle resulting in an increased consumption of the ATP and NADPH [20-22]. In the present review, the energetic and regulatory aspects of the proton potential generation in chloroplasts of higher plants are considered.
TRANSMEMBRANE DIFFERENCE OF HYDROGEN ION ELECTROCHEMICAL
POTENTIALS IN CHLOROPLASTS
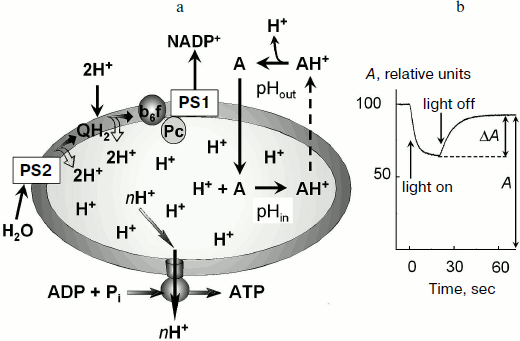
In chloroplasts, Δµ~H+ is generated by activity of proton pumps inserted in the thylakoid membrane (Fig. 1a). Protons released during the decomposition of water in PS2 enter the intrathylakoid space. Oxidation of plastoquinone in the Qo-center of the cytochrome b6f-complex [23-25] is also accompanied by dissociation of protons into the intrathylakoid space. Uptake of hydrogen ions in the stroma is associated with protonation of plastoquinone molecules (Q + 2e– + 2H+ → QH2) that are reduced on the acceptor region of PS2 and in the Qi-center of the cytochrome b6f-complex and also with protonation of NADP+ molecules, which are reduced due to PS1 (NADP+ + 2e– + H+ → NADPH). This results in a decrease in pH of the intrathylakoid space (pHin) and in an increase in pH of the stroma (pHout).
The transmembrane difference of electrochemical potentials of hydrogen ions Δµ~H+ (or the so-called proton-motive force) is determined by two components: the transmembrane difference of electric potentials, Δψ ψin – ψout, and the concentration component determined by the difference in hydrogen ion activities:Fig. 1. a) Mechanism of accumulation of a pH indicator inside the thylakoids in response to light-induced acidification of the intrathylakoid space. b) Change in the amplitude of the low-field component of EPR signal of the spin probe 4-amino-2,2,6,6-tetramethylpiperidine-1-oxyl (TA) (0.3 mM) in a suspension of bean chloroplasts in response to switching on and off white light (from the data of work [50]). The reversible decrease in the EPR signal amplitude (ΔA) is caused by broadening of the EPR spectrum of TA molecules accumulated inside the thylakoids.
Δµ~H+ = FΔψ RT ln([H+]in/[H+]out). (2)
Here [H+]in and [H+]out are activities of hydrogen ions on the two sides of the coupling membrane, R is the universal gas constant, T is temperature (K), and F is the Faraday constant. The concentration component of the proton potential can be expressed as the transmembrane pH difference:
ΔpH = pHout – pHin = log([H+]in/[H+]out).
The Δµ~H+ value expressed in electrical units (mV) at T = 298 K can be written as:
Δµ~H+ = Δψ ·ΔpH. (3)
In energy-converting organelles of animal and plant cells (mitochondria, chloroplasts) and in bacterial cells, Δµ~H+ = 11.6-19.3 kJ/mol, which is equivalent to Δµ~H+ = 160-220 mV. The major part of this energy is used for synthesis of ATP from ADP and Pi.
Both components of Δµ~H+ (electric and concentration) have been experimentally proved to be competent as the sources of energy for operation of ATP synthases of the FoF1 type [26-29]. In mitochondria and bacterial cells, Δµ~H+ is mainly contributed by the electric component (Δψ ≈ 180-200 mV) [5-10]. The inner mitochondrial membrane has a relatively low permeability for ions and, therefore, can successfully sustain the electric potential difference. However, the contribution of the concentration component ΔpH to Δµ~H+ is insignificant. This is due to ion-exchange processes: protons transferred across the coupling membrane bind to proteins and other molecules replacing other ions (e.g. K+). An energetically equivalent exchange of ΔpH for Δψ occurs, and as a result Δψ is the major contributor to Δµ~H+.
In chloroplasts, the picture is the opposite. It is thought that in chloroplasts Δµ~H+ is mainly contributed by the transmembrane difference of pH (ΔpH = 1.5-2.5), whereas the stationary difference in electric potentials is usually not high (Δψ ≤ 10-20 mV) [5-10]. Low values of Δψ are due to a relatively high conductivity of the thylakoid membrane for Mg2+, K+, Na+, and Cl– [30]. In response to the light-induced flow of protons into thylakoids, passive ion flows appear that counteract the generation of Δψ. The ion conductivity of the thylakoid membrane is rather high: t1/2 ≈ 200 µsec where t1/2 is the characteristic time of Δψ dissipation in the dark [31]. However, recent data suggest that under certain conditions in chloroplasts the contribution of Δψ to Δµ~H+ can be higher (10-50% of Δµ~H+ depending on the experimental conditions) [32-34].
The problem of adequate measurement of ΔpH was especially urgent during the early period of development of membrane bioenergetics, when vigorous efforts of the international fellowship of biochemists and biophysicists were directed to creation of a reliable experimental foundation for the chemiosmotic theory (for detail see [35]). It was known then that illumination of chloroplasts leads to uptake of protons and their accumulation inside thylakoids [36]. The classic experiments of Jagendorf and Uribe had shown that an artificial pH gradient in thylakoids provided for significant synthesis of ATP in the dark (~100 ATP molecules per molecule of ATP synthase) [37]. This was many years ago. Quantitative measurements of ΔpH produced conclusive evidence of the energetic role of ΔpH [11-15, 38-43]. However, the question of ΔpH values in chloroplasts remained under intense discussions for a long time because results of ΔpH measurements were often contradictory. Early works reported a rather strong acidification of the intrathylakoid space (pHin < 5.0 at pHout 7.8-8.0) associated with corresponding ΔpH > 3.0-3.5 [42]. Later, experimental data revealed a moderate acidification of the lumen (pHin ~ 5.8-6.5) [12, 44-50]. Discrepancies in the pH determination could be, in particular, caused by differences in the experimental conditions (e.g. differences in osmotic conditions and composition of the incubation medium of the chloroplasts) [51-53].
Kramer et al. [14, 15] have analyzed the literature data for and against high values of ΔpH in photosynthetic systems of the oxygenic type, and they concluded that the intrathylakoid space (or lumen) in chloroplasts should be moderately acidified (pHin ≥ 5.8). An argument for a moderate decrease in pHin is, in particular, the possible inactivation of intrathylakoid proteins at low pH values [14]. The water-splitting complex of PS2 is known to lose its activity at pH < 6.0. A strong decrease in pHin can also promote increased sensitivity of the photosynthetic apparatus to light-induced damage. Plastocyanin, located in the lumen, becomes unstable at pH < 5.5. Experimental confirmations of a moderate acidification of the lumen were obtained by measurements of pHin by the “kinetic” method, using the rate of post-illumination reduction of the oxidized centers P700+ as a measure of pHin in chloroplasts of higher plants in vitro [12, 44, 47] and in situ [14, 46]. The moderate acidification of the intrathylakoid space in chloroplasts functioning under conditions of intense synthesis of ATP is also confirmed by results of our measurements of ΔpH with spin probes [45, 48-50].
Another problem of bioenergetics that was actively discussed in the literature and is still not clear concerns the mechanism of proton transfer coupled to ATP formation by the ATP synthase complex. According to the orthodox version of the chemiosmotic hypothesis formulated in the first works by Mitchell [1, 2] and supported by the majority of his advocates (see, e.g. [5]), the functioning of ATP synthase is associated with transfer of hydrogen ions from the aqueous bulk phase with high proton potential into the aqueous bulk phase with low proton potential (in the case of chloroplasts these phases are the intrathylakoid space and stroma, respectively). An alternative hypothesis about the involvement of protons in energy accumulation was proposed by Williams, who supposed that the key role in formation of the high-energy state should belong to proton-accepting groups located within the coupling membrane (the local coupling mechanism) [54-57]. Ideas similar to this hypothesis were developed by supporters of the micro-chemiosmotic and mosaic concepts of membrane phosphorylation [58-66]. These ideas are supported by data that under certain experimental conditions protons taken up by thylakoids are located within isolated domains and are not in equilibrium with hydrogen ions of the aqueous bulk phase of the intrathylakoid space [64, 65].
Some peculiarities of chemical thermodynamics of small systems. Consider briefly the question of the physical meaning of the concept on the hydrogen ion concentration inside small vesicles. Is it correct to speak about pH inside thylakoids in terms of conventional concepts of physical chemistry? If this is just the case, what meaning must be included into this concept? The essence of the question is that the number of hydrogen ions inside the voluminous aqueous phase of the intrathylakoid space can be very low. Therefore, the question arises about the competence of a formal calculation of hydrogen ion concentration inside thylakoids by the formula [H+]in = nin/vin, where nin is the number of free (not bound to buffer groups) hydrogen ions located in the aqueous (osmotic) phase of the intrathylakoid space with volume vin. Is it correct to use in this case the Nernst formula for calculating the concentration component of Δµ~H+? Specific features of thermodynamics of small systems applied to bioenergetics have been analyzed in several works [6, 67-69].
Under physiological conditions the volume of a thylakoid is estimated to be (1-6)⋅109 Å3 [67]. In this case, at moderate values of pHin the number of free protons nin inside a single thylakoid should be only a few. Thus, at pHin = 6.0 we obtain nin = vin⋅10–pHin = 0.6-3.6. Is it correct to speak about the pHin value if the mean value of nin of free hydrogen ions is only a few? How to treat the concept of hydrogen ion concentration if the probability of detecting even one free hydrogen ion is < 1 (at nin < 1)? This question was discussed in work [69] in which approaches of statistical thermodynamics were used to analyze a reaction of the type PQ ↔ P + Q (an analog of the dissociation reaction AH ↔ H+ + A–). The competence of using approaches of statistical thermodynamics for modeling this reaction is reasonable because the total number of particles P inside small vesicles is high, NPQ + NP >> 1. However, the number of unbound particles P can be very small, NP ~ 1. And in work [69] it was shown that on a decrease in the vesicle volume fluctuations in the number of unbound particles P sharply increase. If the mean number <NP> of free particles P inside a vesicle is only a few (or <NP> < 1), then the law of mass action can be violated because of strong fluctuations. But it should be noted that the Nernst equation for the free energy change on a particle P transferred out from the vesicle remains valid even in the case of small vesicles (at <NP> ≤ 1):
ΔG = –kBT ln(<NP>/coutV), (4)
where kB is the Boltzmann’s constant and the product coutV is the number of free particles P located outside the vesicle in the outer volume V. We emphasize that Eq. (4) is valid for the mean number of free particles P. If <NP> < 1, then <NP> represents the probability of detecting one particle inside one vesicle.
Concerning the problem of proton potential measurement in bioenergetic systems and taking into account these considerations, it should be noted as follows. Using the Eq. (2) to determine the transmembrane difference of electrochemical potentials of hydrogen ions in thylakoids that have a small inner volume is quite reasonable. In chloroplasts, the overwhelming number of protons taken up by thylakoids (~99%) are bound by proton-accepting groups of the thylakoid membrane and buffer groups of molecules located in the intrathylakoid volume [44, 70, 71]. And it can be shown that the presence of a large number of buffer groups has to damp fluctuations of the number of the unbound (water-swimming) hydrogen ions inside the thylakoids.
APPROACHES FOR MEASUREMENT OF PROTON POTENTIAL IN
CHLOROPLASTS
The question “How acidic is the lumen?” bannered as a paper title [14] was extremely poignant during the years of formation of membrane bioenergetics. However, this question has not lost its urgency even at the present. Along with the energetic role as of the primary energy-rich agent, the transmembrane pH difference plays an important role in the regulation of photosynthetic transport of electrons.
Quantitative determination of the ΔpH in chloroplasts is a difficult problem of biophysics. Electron transfer in the ETC of chloroplasts is accompanied by uptake of protons from the outer medium and their release inside the thylakoids. However, the decrease in number of protons in the outer medium does not allow us to determine pHin because it is necessary to know not only the inner volume, but also the effective buffer capacity of proton-accepting groups exposed into the thylakoid lumen. Direct measurements of the concentration (activity) of hydrogen ions inside the thylakoids with pH-sensitive electrodes are difficult because of the small size of these organelles. Most often ΔpH values are measured with pH-sensitive molecular probes [41-43]. One of these methods is based on the use of penetrating amines, which are distributed between the inner volume of the vesicle and the outer medium depending on the transmembrane pH difference (ΔpH). Another approach includes recording spectral (optical, EPR, NMR) responses of pH-sensitive indicators located inside or outside the vesicles (measurement of pHin or pHout, respectively).
Measurement of ΔpH based on distribution of penetrating ions. This method of ΔpH measurement is based on the idea that distribution of probe molecules between the inner and outer spaces is determined by the ratio between activities of hydrogen ions inside and outside the vesicle. To measure ΔpH, penetrating amines that can be accumulated inside thylakoids on decrease in pHin are commonly used. Figure 1 shows schematically that decrease in pHin associated with the activity of ETC of chloroplasts results in accumulation of the probe molecules inside the thylakoids.
The use of penetrating amines is based on the observation that the light-induced decrease in pHin shifts the equilibrium to increase the concentration of protonated (charged) form of the probe inside the thylakoids (A + H+ → AH+). Because deprotonated (uncharged) molecules of the probe can easily penetrate across the thylakoid membrane, it was supposed that the stationary concentrations of the uncharged probe inside and outside the thylakoids should be virtually the same. The penetration of protonated (charged) probe molecules (AH+) across the thylakoid membrane is slower than the penetration of uncharged probe molecules (A). The equilibrium inside the thylakoids is shifted to the charged molecules AH+ and, as a result, the concentration of the probe molecules inside the thylakoids ([A]in) becomes higher than outside ([A]out). It is easy to show that the ratio of the probe concentrations inside and outside the thylakoids is determined by the ratio of hydrogen ion activities ([H+]in and [H+]out, respectively):
[A]in/[A]out = ([H+]in + KA)/([H+]out + KA) [H+]in/[H+]out. (5)
Here KA is the equilibrium constant of the reaction AH+ ↔ A + H+. If the proton-accepting group of the probe has pKA > pHout (i.e. KA << [H+]out [H+]in), then with high accuracy the following approximation is valid:
ΔpH = log([H+]in/[H+]out) ≈ log([A]in/[A]out). (6)
To calculate ΔpH, it is necessary to determine the ratio of the probe concentrations inside and outside the vesicle. The researcher has to measure the number of the probe molecules taken up by the thylakoids (Nin) and then calculate the probe concentrations inside ([A]in) and outside ([A]out) the vesicles. If we know Nin and the inner volume Vin of the particles, it is easy to calculate the ratio of the probe concentrations inside and outside the thylakoids:
[A]in/[A]out = Nin/(N0 – Nin) (V0/Vin – 1), (7)
where V0 is the volume of the chloroplast suspension, N0 is the total number of probe molecules in the suspension equal to N0 = c0V0, and c0 is the mean concentration of the probe in the chloroplast suspension.
Determinations of the number of probe molecules Nin located in the voluminous aqueous phase inside the thylakoids and of the inner volume Vin are often difficult because of side effects. Thus, dyes used as pH probes (9-aminoacridine, Neutral Red, etc. [72-78]) can bind to the thylakoid membrane. Moreover, the probes can bind with the thylakoid membrane not only from the inner, but also from the outer side. The binding of the probe with the membrane can lead to overestimated values of Nin and correspondingly to overestimated values of ΔpH (by 1.0-1.5 pH units). Measurement of the inner value Vin can be difficult because of osmotic effects. Moreover, absorption and fluorescence spectra of the dyes used for ΔpH measurement can overlap with the absorption spectra of photosynthetic pigments. It seems that such artifacts could cause overestimated values of ΔpH in chloroplasts reported in works [38-40]. These difficulties associated with ΔpH measurement can be overcome by using paramagnetic (spin) pH probes.
Spectral methods of ΔpH measurement. These methods are based on the sensitivity of optical, EPR, and NMR absorption spectra of probes and of fluorescence spectra of indicator molecules to changes in pH of the solvent. Dyes with absorption and fluorescence spectra that change on protonation are most often used as optical probes [79-83]. Absorption and fluorescence spectra of a dye located inside the vesicle are a result of superposition of the spectra of the protonated and deprotonated forms of the probe. The ratio between these forms must depend on the pH value inside the vesicle. As mentioned above, some pH indicators used for measurement of the intrathylakoid pHin (including Neutral Red, which is one of the most frequently used pH indicators [78, 81]) bind with the thylakoid membrane. This can be a cause of discrepancies in the pHin measurements in response to light flashes [78, 80, 81].
Use of NMR spectroscopy for pH measurement is based on the protonation-induced change in the chemical shift of 31P nuclei, which are constituents of physiologically important compounds (orthophosphate, creatine phosphate, ADP, ATP, etc.) [83-87]. In practice, the 31P NMR signal of orthophosphate (which is a component of incubation medium of virtually all systems under study) is commonly used as a pH indicator. This is one of significant advantages of the method. Compounds containing 19F nuclei are also used as pH indicators. NMR was successfully used for measurement of pH in bacterial cells and in different compartments of plant and animal cells [83-87]. This method was also used for ΔpH measurements in mitochondria [84] and chromatophores of Rhodopseudomonas sphaeroides [85]. Unfortunately, there are virtually no publications about measurements by the NMR method of intrathylakoid pH in chloroplasts.
Colored fluorescent proteins are now used rather frequently for recording intracellular pH [88-90]. This not only opens unique possibilities for pH measurements but also promotes visualization of the pH distribution inside different compartments of the cell and in energy-converting organelles. In particular, the pH distribution in mitochondrial matrix has been observed with green fluorescent protein [90]. Unfortunately, there are no literature data on pH determination in chloroplasts with fluorescent proteins.
Measurement of ΔpH with spin probes. Stable nitroxyl radicals (spin probes) are widely used as molecular probes sensitive to their local environment [91-101]. EPR spectra of nitroxyl radicals carry information about their mobility, polarity, and the pH of the medium. There are two approaches for determination of ΔpH with nitroxyl radicals. The first approach is based on determination of probe molecules partitioning between the medium and the intrathylakoid volume [91-94], and the other approach is based on recording changes in the EPR spectrum shape caused by protonation of the radicals [97-100]. In the first case paramagnetic amines are commonly used, e.g. 4-amino-2,2,6,6-tetramethylpiperidine-1-oxyl (TA). The great majority of TA molecules taken up by thylakoids are located in the aqueous bulk phase of the intrathylakoid space [50]. This suggests that TA acts as an indicator of the transmembrane difference of pH between the aqueous bulk phases inside and outside the thylakoids. In the other case imidazolidine and imidazoline derivatives of nitroxyl radicals are most often used [97-100]. Both approaches have been used in our determinations of ΔpH in bean (Vicia faba) chloroplasts [45, 48-50, 94-97].
Light-induced uptake of spin probes by chloroplasts. The light-induced acidification of the intrathylakoid space causes accumulation of the penetrating amines inside the thylakoids (Fig. 1a). The measurement of concentration of TA molecules accumulated inside the thylakoids ([TA]in) and of TA molecules which remained outside ([TA]out) allows one to determine ΔpH ≈ log([TA]in/[TA]out). A researcher has to measure the number of molecules of the probe (Nin) taken up and the inner volume (Vin), and to calculate [TA]in = Nin/Vin. Both fractions of the label molecules, those located inside and outside the thylakoids, produce characteristic EPR signals. The EPR signal from the label molecules inside the thylakoids can be isolated from the total EPR signal. In particular, addition to the chloroplast suspension of a paramagnetic broadening agent, which does not penetrate into the thylakoids (e.g. chromium oxalate), results in broadening of the EPR signal from the label molecules outside the thylakoids. The unbroadened EPR signal will belong to the label molecules located inside the thylakoids [50]. The integral intensity of this signal will be proportional to the inner volume of the thylakoids (Vin).
The light-induced uptake of the label by the thylakoids in response to decrease in pHin is most often recorded using the approach based on the effect of concentration-dependent broadening of the EPR spectrum. The concentration of the label inside the thylakoids would lead to broadening the EPR spectrum due to enhancement of the spin-exchange interaction between the radicals colliding with each another inside the thylakoid. If the probe concentration inside the thylakoids is sufficiently high ([TA] ≥ 2-2.5 mM), the EPR signal of the probe is broadened and its amplitude correspondingly decreases [48-50]. As a result, the total EPR signal decreases (Fig. 1b). TA is characterized by a threshold type of concentration-dependent broadening of its EPR spectrum: the broadening occurs only when [TA] ≥ 2-2.5 mM. This specific feature of TA provides the basis for development of an original approach for ΔpH measurement [50], which does not need Vin to be determined. We have used this approach for measurements of ΔpH in isolated bean chloroplasts in metabolic states 3 and 4 [50]. We found that at pHout = 7.8 under conditions of noncyclic electron transport in the thylakoids, ΔpH = 1.96 (state 3) and ΔpH = 2.54 (state 4).
Light-induced changes in EPR spectra of spin probes. The other method for measurement of pHin is based on recording light-induced changes in EPR spectra of protonated spin probes [97-100]. The matter is that the protonation of the probe is accompanied by changes in its EPR spectrum due to redistribution of the spin density on the paramagnetic fragment >N–O• [96]. The most suitable probes for measurements of pHin are imidazolidine and imidazoline derivatives of nitroxyl radicals [95-100].
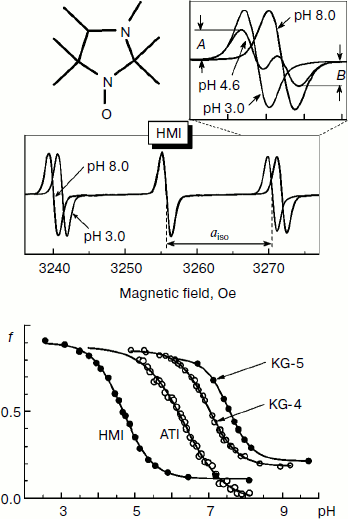
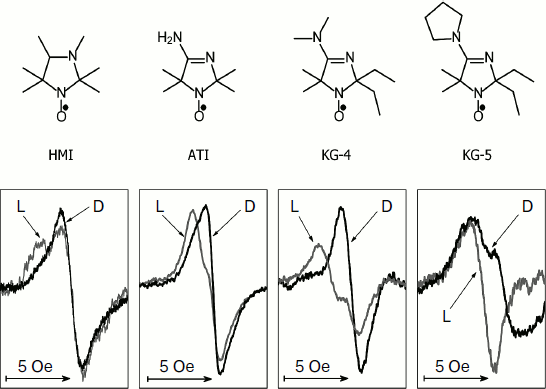
Figure 2 shows the change in the EPR spectrum of the spin probe HMI (2,2,3,4,5,5-hexamethyl-3-imidazolidine-N-oxyl) on varying pH of the solvent. The protonation of the probe decreases the isotropic hyperfine coupling constant (aiso). In the lower part of Fig. 2, the pH dependences of the spectral parameter f = A/(A + B) are presented for four probes [95] that we have used for pHin measurement inside thylakoids of bean chloroplasts [97]. These probes have protonated groups with pKa = 4.7-7.6.
Figure 3 shows high-field components of the EPR spectra of four different spin probes located inside thylakoids. The high-field components are most sensitive to changes in pH. On turning the light on, the EPR spectra change. In all cases the spectral lines are shifted to lower field, which unambiguously indicates a decrease in pHin. The most pronounced changes were observed in EPR spectra of the radicals KG-5 and KG-4 in which pKa of the protonated groups are 7.6 and 7.0, respectively. A clear shift of the spectral line maximum into the low-field region of the spectrum was also recorded for the probe ATI (pKa = 6.2). The spin probe HMI with the lower value of pKa (4.7) displayed less pronounced changes than the probes with higher pKa values. In the case of the HMI probe, only a relatively small shoulder appeared in the low-field part of the spectral line.Fig. 2. Influence of incubation medium pH on parameters of EPR spectra of pH-sensitive spin probes: HMA (2,2,3,4,5,5-hexamethyl perhydroimidazole-1-oxyl), ATI (4-amino-2,2,5,5-tetramethyl-2,5-dihydro-1H-imidazole-1-oxyl), KG-4 (4-dimethylamino-2,2-diethyl-5,5-dimethyl-2,5-dihydro-1H-imidazole-1-oxyl), KG-5 (2,2-diethyl-5,5-dimethyl-4-pirrolidinilyl-2,5-dihydro-1H-imidazole-1-oxyl). In the lower part of the figure the pH dependences of the parameter f = A/(A + B) of EPR spectra of the probes HMA, ATI, KG-4, and KG-5 dissolved in the chloroplast incubation medium are presented (from data of work [95]).
Light-induced changes in EPR spectra of the intrathylakoid pH probes are reversible. Upon turning off the light, the EPR spectra take the initial shape. In the presence of uncouplers (nigericin, gramicidin D, NH4Cl) preventing the generation of ΔpH, no light-induced changes occur. This indicates that the observed changes in the EPR spectra are really caused by acidification of the intrathylakoid space.Fig. 3. Influence of illumination on the shape of the high-field components of EPR spectra of pH-sensitive spin probes HMA, ATI, KG-4, and KG-5 located in the aqueous phase of the intrathylakoid space of bean chloroplasts (from data of work [97]). Gray curves show spectra recorded in the light (L); black curves show spectra recorded in the dark (D).
To determine quantitatively pHin from the EPR spectra of the spin probes, it is necessary to have calibration curves (pHin dependences of the spectral parameters) for the probe molecules located inside the thylakoids. This is necessary because the mobility and polarity of the environment of the probes can be different inside and outside the thylakoids [50]. For the probe ATI the corresponding calibration curves were obtained in work [97]. This probe was used for determination of pHin in bean chloroplasts. Under conditions of photosynthetic control, pHin decreased to 5.4-5.7 (at pHout = 7.8). Under conditions of ATP synthesis (in the presence of excess amounts of Mg-ADP and Pi), the acidification of the intrathylakoid space is less pronounced, pHin > 5.7 (at pHout = 7.8). These data are in agreement with results of ΔpH measurements using uptake of the spin probe TA [45, 50]. Thus, measurements of ΔpH with spin probes based on two independent approaches have shown that ATP is intensively synthesized in isolated bean chloroplasts at ΔpH not higher than 1.8-2.1.
Note in conclusion that along with the indisputable virtues of intrathylakoid pH measurements with spin probes, there are some limitations for using these approaches because of reactivity of nitroxyl radicals (loss of paramagnetism due to their interaction with electron carriers of the ETC and other chemically active compounds [95, 101]).
Kinetic method of measurement of intrathylakoid pH. The kinetic method of pHin measurement is based on the pHin dependence of the electron transfer rate in chloroplasts in the ETC region between PS2 and PS1 [11-14]. Note that within a wide range of experimental conditions (e.g. on varying temperature and ionic strength of the chloroplast suspension [102]), the reduction of plastoquinone in PS2 (Q + 2e– + 2H+out → QH2) and diffusion of QH2 to b6f-complexes occur much faster than the direct oxidation of QH2 by b6f-complex. This means that the stage limiting the electron transfer rate in the region of the ETC between PS2 and PS1 is the pH-dependent reaction of plastoquinone (QH2) oxidation [80], which occurs on the binding of QH2 by the cytochrome b6f-complex [23-25].
The QH2 molecule oxidized by the b6f-complex binds to the so-called Qo-center of the cytochrome complex. Two different electron acceptors are located near the bound QH2 molecule: a high-potential (Fe-S)2 cluster of the Rieske protein and a low-potential heme bL of cytochrome b6 [23-25]. In the Qo-center, the oxidation of two-electron carrier QH2 is associated with a “concerted” transfer of two electrons from one QH2 molecule to two different acceptors [25]. And virtually concurrently with the transfer of one electron to the oxidized iron-sulfur center, the other electron is transferred to the oxidized heme bL. The rate of QH2 oxidation depends on pHin because this reaction is coupled with dissociation of two protons into the intrathylakoid space (QH2 → Q + 2e– + 2H+in). The plastoquinone binding center Qo where QH2 is oxidized is located near the inner side of the thylakoid membrane [23-25], and therefore the rate of QH2 oxidation depends on pHin. The key role in the proton dissociation belongs to the carboxyl group of glutamate (D78), which is located directly nearby the QH2 molecule bound with the Qo-center of the cytochrome complex [23-25, 103]. The probability of proton dissociation decreases due to “pressure” of hydrogen ions accumulated inside the thylakoids, and as a result the rate of QH2 oxidation decreases on the decrease in pHin. Such is one of the pHin-dependent feedback mechanisms that controls the rate of photosynthetic electron transport.
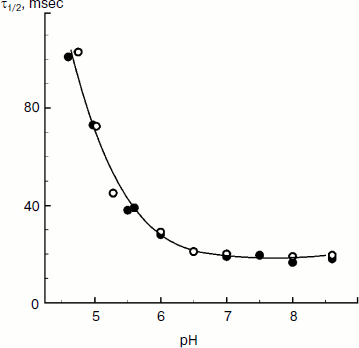
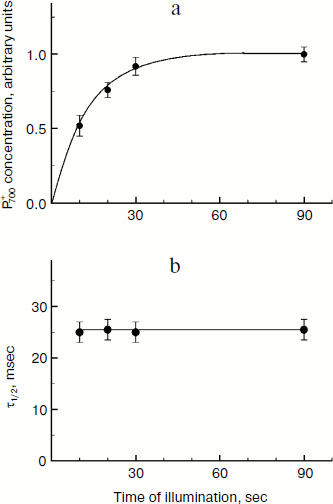
The rate of electron transfer in the ETC region between QH2 and P700 allows us to assess pHin. It is necessary to have a calibration curve of pHin-dependence of the electron transfer rate. This curve can be determined if we find the dependence of the half-reduction time (τ1/2) of P700+ on the pH of the incubation medium of chloroplasts in the presence of protonophores leveling pH inside and outside the thylakoids (pHin = pHout). Figure 4 presents the pH dependence of τ1/2 for bean chloroplasts in the presence of gramicidin D. At moderate decrease in pH (pH 6.5-8.5), τ1/2 is not higher than 20-25 msec. The decrease in the electron transfer rate to P700+ becomes noticeable only on stronger decrease in pH (6.5). Similar pH dependences were obtained from the cytochrome f reduction kinetics in intact spinach (Spinacia oleracea) chloroplasts [14, 47]. It should be emphasized that the kinetic approach gives local values of pHin, i.e. pHin values in the intrathylakoid space regions located near the cytochrome b6f-complex where QH2 is oxidized.
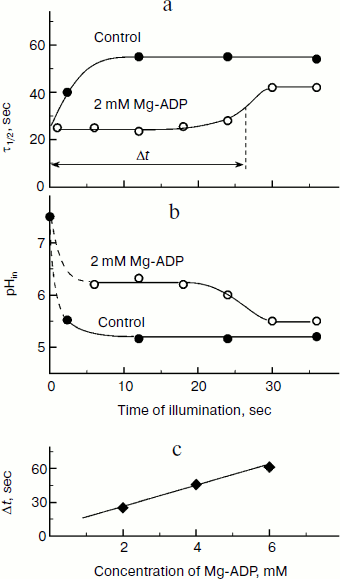
The kinetic approach was first used in 1969 by Rumberg and Siggel [11] for measurement of pHin in spinach chloroplasts. Later we used this approach for measuring pHin in isolated bean chloroplasts [12, 44] and in leaves of higher plants [46]. Figure 5 demonstrates the use of the kinetic method, and one can see that τ1/2 characterizing the rate of electron transfer to oxidized P700+ centers changes on illumination of bean chloroplasts. On illumination of the control chloroplasts (without addition of Mg-ADP, pHout = 7.8), τ1/2 increases to the steady state value of ≈55 msec (Fig. 5a). This value of τ1/2 corresponds to pHin 5.2 (Fig. 5b). On addition to the chloroplasts of 2 mM Mg-ADP, another picture is observed. During the first 20 sec a relatively high rate of electron transfer is retained (τ1/2 ≈ 25 msec). Then, upon the exhaustion of the ADP, the rate of electron transfer decreases, which reflects the transition of chloroplasts from state 3 to state 4 (Fig. 5a). Upon the transition of the chloroplasts to the state of photosynthetic control, the pH inside the thylakoids lowers to pHin 5.5 (Fig. 5b). The time the chloroplasts remain in state 3 (Δt, see the definition in Fig. 5a) is proportional to the concentration of Mg-ADP added to the chloroplasts before the illumination (Fig. 5c).Fig. 4. The pH dependence of the half-reduction time of oxidized P700+ in bean chloroplasts suspended in incubation medium containing 3 µM gramicidin D (from data of works [12, 102]).
An important advantage of the kinetic method is the possibility to measure pHin in chloroplasts both in vivo and in situ, i.e. in plant leaves. The modern biophysical experimental techniques (EPR and optical spectroscopy) allow us to follow electron transfer in optically dense photosynthetic systems. In work [46] the EPR method was used to study kinetics of redox transients of P700 in intact leaves of Hibiscus rosa-sinensis previously adapted to darkness. During the induction phase (the stage of increase in P700+ concentration, Fig. 6a), the characteristic time τ1/2 of electron transfer from the QH2 pool to oxidized centers of P700+ is ≈25 msec (Fig. 6b). Similar values of τ1/2 (20-28 msec) are given in the work of Kramer et al. [14], who determined the kinetics of the reduction of cytochrome f in intact pea, tobacco, and cucumber leaves. According to the calibration curve presented in Fig. 6, τ1/2 ≈ 25 msec corresponds to intrathylakoid pHin ≈ 6.2.Fig. 5. a) Kinetics of changes in τ1/2 depending on duration of the illumination of bean chloroplasts. The parameter τ1/2 characterizes the rate of post-illumination reduction of P700+. Control: chloroplasts in the presence of 10 µM Mg-ATP (without addition of Mg-ADP). b) Kinetics of light-induced changes in intrathylakoid pHin. c) Dependence of the duration of the induction phase (Δt) that characterizes the transition of the chloroplasts from state 3 to the state of photosynthetic control (state 4) on the concentration of Mg-ADP added into the chloroplast suspension before the illumination.
Fig. 6. Kinetics of the light-induced oxidation of P700+ in Hibiscus rosa-sinensis leaves adapted to darkness for 10 min (a) and the dependence of P700+ half-reduction in the dark on duration of exposure to white light (b) (from data of work [46]).
ENERGETICS OF ATP SYNTHESIS IN CHLOROPLASTS
The reversible reaction of ATP synthesis from ADP and Pi (the energy-accepting process) catalyzed by membrane ATP synthases of the FoF1 type is coupled with the energy-donating process of proton transfer. ATP synthase is a macromolecular construction, which couples the energy-donating and energy-accepting processes. For coupling these processes, the following energy relationship must be realized:
nΔµ~H+ ≥ ΔGATP. (8)
Here Δµ~H+ is the transmembrane difference of electrochemical potentials of hydrogen ions, n is the number of hydrogen ions transferred through ATP synthase per synthesized molecule of ATP, ΔGATP is the change in the free Gibbs energy in the reaction of ATP synthesis. On analyzing relationship (8), we will assume that in the chloroplast Δµ~H+ is mainly contributed by the transmembrane pH difference: ΔpH = pHout – pHin.
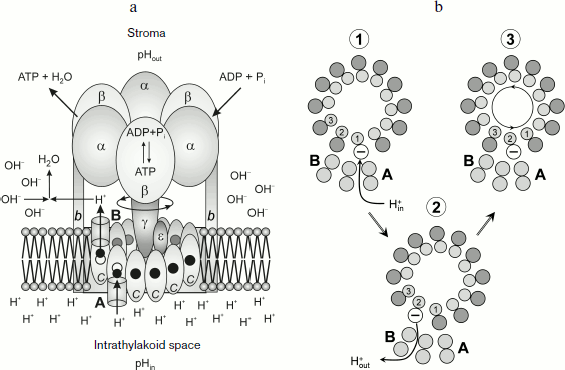
Specific molecular features of the structure of proton ATP synthases responsible for rotation of the rotor Fo. Specific features of the structure of proton ATP synthases of the FoF1 type (Fig. 7a) determine some limitations of values of pHin and pHout that allow this macromolecular complex to provide for the synthesis of ATP. The membrane fragment of ATP synthase (Fo) contains a “rotor”, an oligomeric complex consisting of hydrophobic c subunits [104-111]. The c subunits are hairpin-like and consist of two α-helices. The hairpin loop is oriented towards the stroma; its terminal regions are submerged into the intrathylakoid space. An ensemble of c subunits forms the cm ring. The number of c subunits in the ring is different in different organisms. ATP synthase of animal mitochondria contains eight c subunits (c8) [110]. In ATP synthases of yeast, eubacteria, and plants, the number of subunits m varies from 10 to 15 [104-109]. In chloroplasts of higher plants the cm ring contains 14 [105-108] and in the cyanobacterium Spirulina platensis it has 15 c subunits [106, 107, 109]. The cm ring is adjacent to the hydrophobic a subunit submerged into the membrane. The polypeptide chain of the a subunit contains five or six transmembrane α-helical regions [112, 113].
The key role in the transmembrane proton transfer across Fo is played by two conservative amino acid residues – Glu61 located in the central part of the outer α-helix of the cm ring and arginine of subunit a (aArg210 in Escherichia coli) which is located on the fourth α-helix directly adjacent to the ring of the c subunits. On the border between subunit a and the cm ring are proton-conducting pathways (half-channels A and B) that are involved in proton transfer from the intrathylakoid volume (“acidic reservoir”) into the stroma (“alkaline reservoir”). Structural and biochemical data [114-118] indicate that the transmembrane proton transfer is associated with a directed rotation of the cm ring. The rotation of the rotor cm was shown using three different approaches: chemical crosslinks leading to immobilization of the rotor [114]; fluorescent probes [115]; and by immediate observation of rotations of individual molecules [116-118].Fig. 7. a) Scheme of the ATP synthase complex. b) Scheme of protonation (stage 1) and deprotonation (stage 2) of c subunits of the oligomeric complex cm and its turn inside the membrane by angle φ 2π/m (stage 3).
In ATP synthase of chloroplasts, the proton carried through Fo is bound with the carboxyl group of amino acid residue Glu61 of the c subunit. This group is located in the hydrophobic center of the cm ring and is surrounded by amino acid residues Leu57, Phe59, Ala62, and Leu63 [108]. The proton transfer through Fo includes stages of protonation and deprotonation of carboxyl groups of the cm ring:
–COO– + H+in → –COOH → –COO– + H+out. (9)
As shown in works [108, 111], conservative carboxyl groups of the c subunits of ATP synthases from different organisms have relatively high pKa values. It has been shown by 1H-NMR spectroscopy that in E. coli the amino acid residue Asp61 of the c subunit in the purified protein is characterized by pKa 7.1, which is noticeably higher than corresponding values of the carboxyl groups of amino acid residues Asp7 and Asp44 (5.4 and 5.6, respectively) [111]. For the carboxyl group of Glu61 in spinach chloroplasts, the pKa value is ~7.3 (computed on the basis of structural coordinates) [108].
The carboxyl group of Glu61 acts as an acceptor of a proton entering from the acidic reservoir. Protonated c subunits move in a circle together with the cm ring and release in turn their protons into the alkaline reservoir (Fig. 7b). It is usually thought that protons come to carboxyl groups of the cm ring from the acidic reservoir through channel A (the input channel). The proton dissociation towards the alkaline reservoir is associated with proton transfer though channel B (the output channel). Using the kinetic model of proton energy accumulation as elastic deformations of the γ subunit, the authors of work [119] assessed pK values of key proton-carrying groups that determine the proton transfer in half-channels A and B. They obtained pKA = 5.3-6.4 and pKB = 8.0-8.3. However, the nature of the input and output proton channels is still enigmatic. According to X-ray crystallographic data [108], there are no visible proton channels in the cm ring either from the thylakoid lumen side (the acidic reservoir) or from the stroma side (the alkaline reservoir). It was supposed in [108] that dynamic fluctuations of the protein could produce proton-conducting pathways that are invisible in the static picture obtained by X-ray crystallography. But it is more likely that proton-conducting channels are formed by α-helices of the a subunit containing a conservative arginine residue that plays a key role in the activity of the Fo motor.
Carboxyl groups can be accessed to input channel A and to output channel B due to rotation of the cm ring (Fig. 7b). Specific features of the structure of membrane motor Fo make the cm rotor a kind of molecular Brownian ratchet [120-122] that rotates directly due to non-coaxial arrangement of half-channels A and B (Fig. 7a). The cm ring is mechanically bound with another rotor, the elongated subunit γ projecting from the α3β3 hexamer towards the membrane. Rotation of subunit γ coupled with the cm ring induces cooperative conformational rearrangements of the α3β3 hexamer, resulting in the catalytic cycle of the ATP synthesis reactions. The catalytic cycle includes processes occurring in three catalytic centers by the so-called binding change mechanism suggested by Boyer [123]. The open catalytic center binds the reaction substrates ADP and Pi; in the closed catalytic center ATP is produced from ADP and Pi (this reaction is thought to be energetically “gratis”). Conformational changes caused by rotation of the γ subunit are responsible for opening of the third catalytic center and for dissociation of the ATP molecule (molecular mechanisms of the activity of F1 are considered in reviews [123-127] and in special issues of journals [128-130]).
How and due to what energy does the cm rotor of the Fo molecular motor rotate? At present, most authors believe that the directed rotation of the cm ring is realized by the mechanism of Brownian rotational fluctuations [120-122]. Jump-like turns of the rotor on the angle φ = 2π/m coupled with translocation of one proton through Fo are thought to occur as a result of random fluctuations due to thermal energy of the environmental medium (“thermostat”). The direction of the rotor rotation is provided for by the structure of molecular motor Fo in the presence of transmembrane difference of electrochemical potentials of hydrogen ions. The provision of energy for discrete turns of the cm ring taken from the thermostat does not mean that the directed rotation of the cm rotor and the γ subunit coupled with it leads to cooling of the thermostat. This would contradict the Second Law of Thermodynamics. Consumption of heat energy of the thermostat for driving different steps of operation of the molecular motor is compensated by heat release during exothermic reactions coupled with the transmembrane proton transfer. If ΔpH is the driving force for the operation of ATP synthase, then the resulting thermal effect (ΔH) can be assessed as the sum of the thermal effects of dissociation of an acid AH in the acidic reservoir (AHin ↔ A– + H+in) and of protonation of buffer groups B– in the alkaline reservoir (B– + H+out ↔ BH). Taking into account that pKB values of buffer groups in the alkaline reservoir are usually higher than pKA values of buffer groups in the acidic reservoir, it is easy to show that the proton transfer through Fo must be an exothermic process (ΔH < 0). This is a consequence of an increase in the thermal effect of dissociation of acidic groups with increase in pK [131]. The ATP synthase is a macromolecular device that prevents the full dissipation to heat of free energy released upon the transmembrane transfer of protons. A significant part of this energy is stored as energy of long-lived elastic deformations of protein subunits of the ATP synthase [119, 132, 133], which is used for the directed rotation of the γ subunit [134-136], conformational rearrangements of the α3β3 hexamer, and for ATP synthesis [128-130].
Energy balance of proton transport reactions and ATP synthesis. Obviously, if ΔpH is the driving force for the operation of ATP synthase, the directed rotation of the membrane rotor cm can occur only under the following conditions:
pHin < pKa (10)
(protonation of the carboxyl group of subunit c due to hydrogen ions entering from the intrathylakoid space),
pKa < pHout (11)
(deprotonation of the carboxyl group of subunit c due to proton dissociation into the stroma); pKa is the effective value of pK of the acidic group of the proton-transporting subunit c.
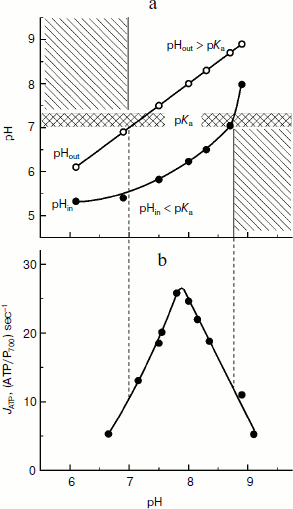
It is clear that under conditions favorable for ATP synthesis in chloroplasts, relations (10) and (11) are valid. Note that for the carboxyl group Glu61 of subunit c, pKa = 7.1-7.3. In the case of bean chloroplasts (Fig. 8a), inequalities pHin ≤ pKa ≤ pHout are valid over a rather wide range of external medium pH (pHout = 7.0-8.6). And it is interesting that just in the same limits of pHout ATP is intensively synthesized with maximum at pH values of 7.8-8.0 (Fig. 8b). In native chloroplasts in situ, pHin ≈ 6.2 < pKa [14, 46] and the stationary value of the stroma pH is pHout ≈ 7.8-7.9 > pKa [137, 138], i.e. conditions necessary for effective synthesis of ATP are also present.
The concentration (ΔpH) and electric (Δψ) components of Δµ~H+ are considered [26-29] to be energetically equivalent components of the proton potential. This means that the directed rotation of the cm rotor can occur at ΔpH = 0 (pHin = pHout) if there is a sufficiently high difference of electric potentials between the aqueous bulk phases separated by the thylakoid membrane, Δψ = ψin – ψout. The exact molecular mechanism of the rotation of the cm rotor due to Δψ is still unknown. It is supposed that if Δψ is the motive force for the ATP synthase activity, the proton transfer from the intrathylakoid space into the stroma is caused by a potential-dependent modulation of effective values of pKa of functional groups of the rotor induced by changes in their positions relatively to half-channels A and B. In the first approximation, the effective value of pKaeff of the acidic group can be assessed by the formula:Fig. 8. a) Dependence of intrathylakoid pHin on pH of the incubation medium of bean chloroplasts (pHout). The pHin was measured with the spin probe TA. b) Dependence of the ATP synthesis rate in bean chloroplasts on pH of the incubation medium of bean chloroplasts (pHout) (from data of work [45]).
pKaeff = pKa – (F/RT)Δψloc,
where Δψloc is the energy-dependent change in the electric potential in the vicinity of the protonated acidic group. The potential-dependent modulation of pKaeff values can be associated with the influence of electric potential on local pH values near the acidic groups.
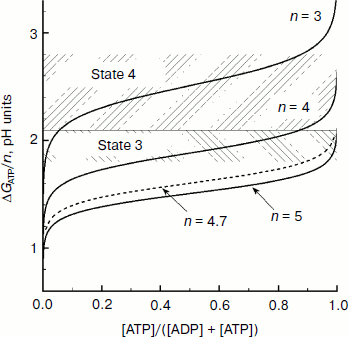
Consider if the energy stored in chloroplasts as the concentration component of the proton potential ΔpH is sufficient to achieve conditions of energy balance nΔµ~H+ ≥ ΔGATP? The free energy of ATP synthesis can be determined from the equation:
ΔGATP = ΔGATP0′ + RT ln([ATP]/([ADP][Pi])), (12)
where [ATP], [ADP], and [Pi] are concentrations of the reactants, and ΔGATP0′ is the standard Gibbs free energy of ATP synthesis. According to [139, 140], under conditions similar to those of generation of ΔpH = 1.8-2.1 (pHout 7.8, [Mg2+] = 5 mM, T = 295 K), ΔGATP0′ = 30.5 kJ/mol. Other evaluations [141] give ΔGATP0′ = 31.2 kJ/mol, and the main contribution toΔGATP0′ is the enthalpy component ΔHATP0′ = 28.1 kJ/mol. The standard entropy of the reaction is not high, ΔSATP0′ = –11 J/(mol·K). Accurate measurements of the rate of ATP synthesis depending on the phosphate potential in spinach leaves recently performed by Graber et al. [142, 143] resulted in ΔGATP0′ = 37-38 kJ/mol.
Having in mind the equation of material balance for ATP, ADP, and Pi, Eq. (12) can be rewritten as follows:
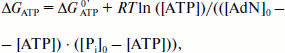 (13)
(13)
Figure 9 presents dependences of ΔGATP on the relative concentration of ATP calculated for some values of n = H+/ATP at [AdN]0 = 4 mM and [Pi]0 = 10 mM. In earlier works it was taken that H+/ATP = 3 [144, 145]. According to later biochemical data, n = 4 [141-146]. A “mechanistic” evaluation based on structural data suggests that in chloroplasts H+/ATP ≥ 4. In chloroplasts of higher plants the membrane rotor of the ATP synthase consists of 14 c subunits [105, 108]. If for one full rotation of the c14 rotor 14 protons are transferred outside and three ATP molecules are synthesized, then a fractional value of H+/ATP ≈ 4.7 is formally obtained. This means that for synthesis of one ATP molecule the enzyme accumulates energy of at least four or five protons that are transferred through the ATP synthase1.
1 The fractional stoichiometry H+/ATP seems to mean that the bond between the two rotors of the ATP synthase complex, the c14 ring (the membrane part of Fo), and the γ subunit (coupling factor F1) is not rigidly fixed, i.e. one rotor can slide relative to the other. Assume that under stationary conditions the proton-motive force Δµ~H+ is stored in chloroplasts mainly as ΔpH and that n = 4, then the transmembrane pH difference ΔpH = 1.8-2.1 is sufficient for synthesis of ATP at the phosphate potential ΔGATP = 41-48 kJ/mol (equivalent to ΔpH = 1.8-2.1). In intact chloroplasts ΔGATP is 40-50 kJ/mol [147]. At n = 5, the energy of proton gradient ΔpH = 1.8-2.1 is quite sufficient for ATP synthesis at ΔGATP ≈ 51-58 kJ/mol. And it follows that at n = 5 the energy stored by chloroplasts as ΔpH is sufficient for ATP synthesis even at very high values of the phosphate potential. Thus, for example, Fig. 9 shows that at n = 5 the condition ΔGATP/n < ΔpH ≈ 1.8-2.1 is valid at [ATP]/[ADP] >> 10. On illumination of intact spinach chloroplasts, the relative concentration of ATP becomes 0.45-0.66 (depending on the conditions of the experiment) [147]. Thus, it can be concluded that the energy stored in chloroplasts as the concentration component of the proton potential ΔpH is sufficient to provide the energy needed for ATP synthesis.Fig. 9. Dependence of ΔGATP/n on the relative concentration of ATP (from data of work [97]).
THE pH-DEPENDENT REGULATION OF ELECTRON TRANSPORT IN
CHLOROPLASTS
In photosynthetic systems of oxygenic type (cyanobacteria, algae, and chloroplasts of higher plants) the light-dependent stages of photosynthesis are regulated by different mechanisms that provide for the optimal functioning of the photosynthetic apparatus and its protection against stress caused by changes in the environment (intense light, temperature, gas composition of the atmosphere, humidity) [148, 149]. The main mechanisms of the pH-dependent regulation of the light-dependent stages of photosynthesis are as follows:
– regulation of electron transfer rate between PS2 and PS1 depending on the phosphate potential (photosynthetic control) [11-15];
– dissipation as heat of excess energy of solar light absorbed by the PS2 light-harvesting antenna [16-19, 149];
– activation of the Calvin–Benson cycle enzymes [150, 151];
– activation of ATP synthase [144];
– redistribution of electron flows (non-cyclic, cyclic, and pseudo-cyclic electron transport) [152];
– redistribution of light energy between light-harvesting antennas of PS2 and PS1 (state 1 ↔ state 2 transitions) [153].
Consider briefly the mechanisms of pH-dependent regulation of electron transport in chloroplasts associated with acidification of the intrathylakoid space (pHin↓) and with alkalization of the stroma (pHout↑) that are responsible for the optimal stoichiometry of reactions of ATP synthesis and of NADPH formation and that also minimize the risk of damage to the photosynthetic apparatus under excessive solar illumination.
A generalized scheme of pH-dependent regulatory controls in chloroplasts is presented in Fig. 10. Hatched arrows with the sign “–” indicate negative feedbacks (inhibition of the electron transport between PS2 and PS1 at pHin↓, a decrease in the photochemical activity of PS2 at pHin↓, deceleration of protonation of plastoquinone reduced by PS2 at pHout↑). Hatched arrows with the sign “+” indicate positive feedbacks (stimulation of ATP synthesis at pHin↓, activation of the Calvin–Benson cycle reactions and of ATP synthase at pHout↑). Taking into account these positive and negative feedbacks, a researcher can quantitatively describe complex multiphasic kinetics of electron and proton transport in chloroplasts in situ under different environmental conditions (varied contents of CO2 and O2 in the atmosphere) using a mathematical model of the light-driven stages of photosynthesis [154].
“Photosynthetic control” of electron transport. In chloroplasts, as in mitochondria, the rate of electron transport depends on the metabolic state of the organelles, which can be characterized by value of the phosphate potential, Q = [ATP]/([ADP][Pi]). Under conditions of intensive synthesis of ATP (excess of ADP and Pi, state 3), the rate of electron transport remains at a high level. Upon exhaustion of the pool of ADP molecules, the electron transport decelerates (the state of photosynthetic control or state 4). The rate of electron transport depends on phosphate potential by the feedback mechanism mediated through changes in intrathylakoid pHin. A decrease in pHin inhibits the electron transport at the limiting stage in the electron transport chain between PS2 and PS1 – the rate of plastoquinol oxidation by the cytochrome b6f-complex decreases. This leads to a decrease in electron flow from PS2 to oxidized centers P700+ [11-15, 44].Fig. 10. Scheme of positive and negative feedbacks that determine the pH-dependent regulation of electron transport in chloroplasts. CBC, the Calvin–Benson cycle.
Under conditions of intensive synthesis of ATP (state 3), protons are released outside the thylakoids through actively working ATP synthases. The release of protons through ATP synthases prevents a strong decrease in pHin. In the meantime, due to moderate acidification of the intrathylakoid space, the rate of electron transfer between PS2 and PS1 in state 3 remains high (Fig. 5a). This is associated with intensive functioning of “proton pumps”, and pHin is sustained at the level sufficient for synthesis of ATP. In isolated bean chloroplasts in the state 3, pHin becomes 6.2 (Fig. 5b). In the state of photosynthetic control (upon the exhaustion of ADP) the proton outflow from thylakoids through ATP synthase is slowed, pHin decreases more strongly (pHin 5.2), and the electron transport correspondingly decelerates more significantly. In the intact chloroplasts in situ, the characteristic time of electron transfer between PS2 and PS1 τ1/2 ≈ 25 msec (Fig. 6) corresponds to the pHin value of 6.2.
Regulation of PS2 activity. In native chloroplasts in situ (plant leaves), the rate of photosynthetic electron transport depends on pre-illumination history (the duration of plant adaptation to darkness or light having a particular spectrum). The dependence of time course of photosynthetic processes on the prior illumination was termed the induction effects of photosynthesis [155-158]. These effects include the well-known Kautsky effect that manifests itself as non-monotonic changes in the quantum yield of chlorophyll fluorescence in oxygenic photosynthetic systems [155, 158]. Decrease in quantum yield of fluorescence is, in particular, caused by an enhancement in thermal dissipation of energy of excited chlorophyll molecules of the PS2 light-harvesting antenna (non-photochemical quenching (NPQ)) [16-19]. NPQ of chlorophyll excitation in the PS2 light-harvesting antenna plays a protective role, decreasing the probability of damage to the photosynthetic apparatus under conditions of light-induced stress. A decrease in pHin acts as a signal for enhancement of the dissipation of excess energy, which induces rearrangements in the photosynthetic apparatus leading to strengthening of NPQ. In chloroplasts of higher plants, activation of NPQ is initiated by protonation of the protein subunit PsbS, which is a component of PS2 [17], and by the xanthophyll cycle reactions resulting in de-epoxidation of violaxanthin producing zeaxanthin [16-19, 149].
Activation of Calvin–Benson cycle reactions. The acceptor side of PS1 is another segment of the ETC where the pH-dependent regulation of electron transport in chloroplasts is realized. Here we must mention redox-dependent modulation of activities of different enzymes that are mediated through the thioredoxin/thioredoxin reductase system [150]. During the initial period of illumination of dark-adapted intact chloroplasts (during the induction period), the electron outflow from PS1 to NADP+ is limited by the low rate of functioning of the Calvin–Benson cycle where NADP+ is regenerated. The excess of reductants in PS1 is used for reduction of thioredoxin that, in turn, activates other enzymes, including those of the Calvin–Benson cycle. Upon activation of the Calvin–Benson cycle, the electron outflow from PS1 to NADP+ is accelerated.
The light-induced alkalization of the stroma is important for activation of the Calvin–Benson cycle. On illumination, the stromal pH increases from the initial pHout value of 7.0-7.2 to 7.8-7.9 [137, 138]. The increase in pHout is caused by proton consumption due to protonation of plastoquinone (Q + 2e– + 2H+ → QH2) and NADP+ reduction (NADP+ + 2e– + H+ → NADPH). The increase in pHout is accompanied by an increase in Mg2+ concentration in the stroma, which is necessary for activation of rubisco, which is the key enzyme of the Calvin–Benson cycle catalyzing fixation of CO2. The activation of the Calvin–Benson cycle results in acceleration of consumption of NADPH and ATP and, as a consequence, in the increase in electron outflow from PS1. Consider as an example the kinetics of P700 photooxidation in dark-adapted leaves of H. rosa-sinensis (Fig. 6). Switching on the light increases the concentration of oxidized P700+, which reaches the stationary level after about 30 sec of illumination (Fig. 6a). The kinetics of P700 photooxidation is determined by the balance of two processes: electron outflow from PS1 and the electron inflow to P700+ from PS2. The decelerated growth of [P700+] is caused by acceleration of the electron outflow from PS1 due to activation of the Calvin–Benson cycle. In the presence of methyl viologen, which serves as an artificial mediator of electron transfer from PS1 to molecular oxygen, the growth of [P700+] is much faster because in this case the electron outflow from PS1 is not limited by the Calvin–Benson cycle activity on starting the illumination of the leaves [46]. The rate of electron inflow to P700+ remains unchanged during the whole induction phase (10-90 sec) (Fig. 6b). The characteristic time of electron transfer to P700+ is τ1/2 ≈ 25 msec, which corresponds to pHin ≈ 6.2.
Activation of ATP synthase. The enzymatic activity of ATP synthase is determined by several factors. It is well known that the light-induced activation of ATP synthase of chloroplasts occurs due to the light-induced energization of the thylakoid membrane [159, 160]. ATP synthase of chloroplasts can be activated upon a preliminary generation of Δµ~H+ and reduction of thiol groups in the regulatory domain of subunit γ (fragment Cys199-Cys205 in spinach chloroplasts). Reduction of thiol groups of subunit γ is accelerated on the energization of chloroplasts [161, 162]. The chloroplast energization is thought to induce conformational changes in the enzyme and thus to make easier the access to the thiol groups. In chloroplasts in vivo, the γ subunit is reduced by thioredoxin, which receives electrons from PS1 through thioredoxin reductase [163-165]. The redox-dependent regulation of the activity is an “exclusive” feature of ATP synthase of chloroplasts, the subunit γ of which contains thiol groups. ATP synthases of other origin do not have a mechanism of regulation of enzymatic activity mediated through reduction/oxidation of thiol groups.
The mechanism of activation of ATP synthase of chloroplasts seems to be associated with conformational changes of the enzyme. There were very demonstrative experiments with a chimeric complex α3β3γ of the thermophilic bacterium Bacillus PS3 [166]. It this complex, the central part of subunit γ was substituted by an equivalent fragment of the subunit γ of spinach chloroplasts containing cysteine residues. Rotations of subunit γ inside the α3β3 hexamer was measured in real-time, and the rate of the rotor rotation was shown to depend on the redox-state of the enzyme. Upon reduction of the disulfide bridge (–S–S– → –SH + SH–) in the regulatory region of the subunit γ, the rate of directed rotation of the rotor noticeably increased together with the ATPase activity of the enzyme.
On de-energization of chloroplasts in the dark, the activity of ATP synthase decreases. To completely deactivate ATP synthase of chloroplasts, it must be oxidized. Kramer and Crofts have shown [167, 168] that in intact leaves in the dark ATPase is deactivated relatively slowly – the characteristic time of the decrease in ATPase activity in the dark is ~20 min. This means that a short-term shadowing of leaves (e.g. by clouds passing before the Sun) is insufficient to fully deactivate ATP synthase [157]. The nature of the physiological oxidant for ATP synthase remains unclear. It is supposed that in the single-cell alga Dunaliella salina, L-1-N-methyl-4-mercaptohistidine disulfide [169] may be a physiological oxidant for ATP synthase.
Recent new data suggest that the minor subunit ε, which is a component of F1’s rotor shaft, can be involved in the modulation of activities of proton ATP synthases. The ε subunit is directly bound with the part of the γ subunit that is projected from the α3β3 hexamer and clings to the cm ring of the membrane complex Fo. The ε subunit is thought to be capable of rotating together with the γ subunit and of being responsible for the mechanical contact of the rotor F1 with the cm ring. The ε subunit is shown to decelerate the rotation of the F1-ATPase rotor, acting as an “inner” inhibitor of ATPase and preventing useless expenditure of ATP [170]. The mechanism of the auto-inhibitory action of ε subunit in ATP synthases of plant and bacterial origin became clear after the appearance of recent data on the structure of the catalytic complex of F1-ATP synthase from E. coli in different states [171]. In the active state (state εC), ε subunit has a compact conformation. Two α-helical C-terminal domains of ε subunit are turned towards the outer part of the γ subunit and therefore do not prevent its rotation inside the α3β3 hexamer. In the inactive state (state εX), the polypeptide chain of the subunit ε straightens: the α-helical domains bound to one another with a hinge turn towards the α3β3 hexamer and penetrate into the central cavity of α3β3, thus impeding the rotation of γ subunit inside F1.
The physiological reason for increase in the activity of ATP synthase of chloroplasts on illumination but suppression in the dark is obvious. ATP synthase is a reversible molecular machine capable of both synthesizing and hydrolyzing ATP. Upon illumination of chloroplasts, when Δµ~H+ generation is higher than the threshold level required for the synthesis of ATP, the enzyme actively functions to synthesize ATP. Although active ATP synthase can also hydrolyze ATP, during illumination the synthesis of ATP is the resulting process. High rates of turnover of activated ATP synthases sustain the intensive synthesis of ATP molecules consumed in the Calvin–Benson cycle during illumination. Under conditions when ATP synthases operate actively (metabolic state 3), pHin moderately decreases, which is necessary to provide for synthesis of ATP. In the meantime, the high rate of non-cyclic electron transport is supported (Fig. 6). In the dark, when the conditions for ATP synthesis in chloroplasts are absent (Δµ~H+ ≈ 0), the high activity of ATP synthases would lead to an unreasonable expenditure of ATP. However, the dissipation Δµ~H+ in the dark, oxidation of the enzyme, and conformational rearrangements of the ε subunit result in inactivation of ATP synthase. Thus, in the dark futile hydrolysis of ATP molecules synthesized by the plant cell mitochondria is prevented.
I want to thank professors L. A. Blumenfeld and E. K. Ruuge, whose support and attention I felt for many years, as well as my biophysics colleagues with whom I had a fortune to study energy and regulatory processes in chloroplasts. Experimental results presented in this article were obtained in cooperation with G. B. Khomutov, A. A. Timoshin, S. B. Ryzhikov, M. Masarova, S. G. Gilmiyarova, S. G. Magnitsky, B. V. Trubitsin, V. V. Ptushenko, R. V. Agafonov, and I. V. Kuvykin. I am deeply grateful to all of them. I am also grateful to the reviewer for attentive reading of the article and useful advice.
This article is dedicated to the memory of E. A. Liberman, a pioneer of membrane bioenergetics. Liberman made fundamental contributions to the understanding of the energetic role of the proton potential in energy-converting organelles in living cells [3, 4]. The unique image of E. A. Liberman will remain forever in the memory of everybody who was lucky to know him.
This work was supported in part by the Russian Foundation for Basic Research (project 12-04-01267a).
REFERENCES
1.Mitchell, P. (1961) Nature, 191,
144-148.
2.Mitchell, P. (1966) Biol. Rev., 41,
445-502.
3.Skulachev, V. P., Sharaf, A. A., and Liberman, E.
A. (1967) Nature, 216, 718-719.
4.Liberman, E. A., Topaly, V. P., Tsofina, L. M.,
Jasaitis, A. A., and Skulachev, V. P. (1969) Nature, 222,
1076-1078.
5.Skulachev, V. P. (1988) Membrane
Bioenergetics, Springer-Verlag, N. Y.
6.Blumenfeld, L. A., and Tikhonov, A. N. (1994)
Biophysical Thermodynamics of Intracellular Processes. Molecular
Machines of the Living Cell, Springer-Verlag, N. Y.
7.Nickolls, D. G., and Ferguson, S. J.
(2002) Bioenergetics 3, Academic Press, Inc., N. Y.
8.Blankenship, R. E. (2002) Molecular Mechanisms
of Photosynthesis, Blackwell Science,
Oxford-London-Edinburgh-Maiden-Carlton-Paris.
9.Nelson, D. L., and Cox, M. M. (2005) Lehninger
Principles of Biochemistry, 4th Edn., Worth Publishers, N. Y.
10.Skulachev, V. P., Bogachev, A. V., and
Kasparinsky, F. O. (2010) Membrane Bioenergetics: A Text-book
[in Russian], MGU Publishers, Moscow.
11.Rumberg, B., and Siggel, U. (1969)
Naturwissenschaften, 56, 130-132.
12.Tikhonov, A. N., Khomutov, G. B., Ruuge, E. K.,
and Blumenfeld, L. A. (1981) Biochim. Biophys. Acta, 637,
321-333.
13.Sigalat, C., Haraux, F., and de Kouchkovsky, Y.
(1993) Biochemistry, 32, 10193-10200.
14.Kramer, D. M., Sacksteder, C. A., and Cruz, J. A.
(1999) Photosynth. Res., 60, 151-163.
15.Kramer, D. M., Sacksteder, C. A., and Cruz, J. A.
(2003) Trends Plant Sci., 8, 27-32.
16.Demmig-Adams, B. (1990) Biochim. Biophys.
Acta, 1020, 1-24.
17.Li, X.-P., Gilmore, A. M., Caffarri, S., Bassi,
R., Golan, T., Kramer, D., and Niyogi, K. K. (2004) J. Biol.
Chem., 279, 22866-22874.
18.Ruban, A. V., Johnson, M. P., and Dufy, C. D. P.
(2012) Biochim. Biophys. Acta, 1817, 167-181.
19.Jahns, P., and Holzwarth, A. R. (2012)
Biochim. Biophys. Acta, 1817, 182-193.
20.Werdan, K., Heldt, H. V., and Milovancev, M.
(1975) Biochim. Biophys. Acta, 396, 276-292.
21.Mott, K. A., and Berry, J. A. (1986) Plant
Physiol., 82, 77-82.
22.Andersson, I. (2008) J. Exp. Botany,
59, 1555-1568.
23.Stroebel, D., Choquet, Y., Popot, J.-L., and
Picot, D. (2003) Nature, 426, 413-418.
24.Kurisu, G., Zhang, H., Smith, J. L., and Cramer,
W. A. (2003) Science, 302, 1009-1014.
25.Cramer, W. A., Zhang, H., Yan, J., Kurisu, G.,
and Smith, J. L. (2006) Annu. Rev. Biochem., 75,
769-790.
26.Graber, P., and Witt, H. T. (1976) Biochim.
Biophys. Acta, 39, 141-163.
27.Hangarter, R. P., and Good, N. E. (1982)
Biochim. Biophys. Acta, 681, 397-404.
28.Graber, P. (1982) Curr. Topics Membr.
Transp., 16, 215-245.
29.Junesch, U., and Graber, P. (1991) FEBS
Lett., 294, 275-278.
30.Barber, J. (1976) in The Intact
Chloroplast, Vol. 1 (Barber, J., ed.), Elsevier, Amsterdam, pp.
88-134.
31.Nishio, J. N., and Whitmarsh, J. (1991) Plant
Physiol., 95, 522-528.
32.Cruz, J. A., Sacksteder, C., Kanazawa, A., and
Kramer, D. M. (2001) Biochemistry, 40, 1226-1237.
33.Cruz, J. A., Kanazawa, A., Treff, N., and Kramer,
D. M. (2005) Photosynth. Res.,
85, 221-233.
34.Takizawa, K., Cruz, J. A., Kanazawa, A., and
Kramer, D. M. (2007) Biochim. Biophys. Acta, 1767,
1233-1243.
35.Boyer, P. D., Chance, B., Ernster, L., Mitchell,
P., Racker, E., and Slater, E. C. (1977) Annu. Rev. Biochem.,
46, 955-1026.
36.Neumann, J., and Jagendorf, A. N. (1964) Arch.
Biochem. Biophys., 107, 109-119.
37.Jagendorf, A. T., and Uribe, E. (1966) Proc.
Natl. Acad. Sci. USA, 55, 170-177.
38.Rottenberg, H., Grunwald, T., and Avron, M.
(1972) Eur. J. Biochem., 25, 54-63.
39.Schuldiner, S., Rottenberg, H., and Avron, M.
(1972) Eur. J. Biochem., 25, 64-70.
40.Rottenberg, H., and Grunwald, T. (1972) Eur.
J. Biochem., 25, 71-74.
41.Rottenberg, H. (1979) Meth. Enzymol.,
55, 547-575.
42.Pick, U., and McCarty, R. E. (1980) Meth.
Enzymol., 69, 538-546.
43.Azzone, G. F., Piewboron, D., and Zoratti, M.
(1984) Curr. Topics Bioenerg., 13, 1-77.
44.Tikhonov, A. N., and Timoshin, A. A. (1985)
Biol. Membr. (Moscow), 2, 349-362.
45.Tikhonov, A. N., and Timoshin, A. A. (1985)
Biol. Membr. (Moscow), 2, 608-622.
46.Ryzhikov, S. B., and Tikhonov, A. N. (1988)
Biofizika, 33, 642-646.
47.Nishio, J. N., and Whitmarsh, J. (1993) Plant
Physiol., 101, 89-96.
48.Magnitsky, S. G., Masarova, M., and Tikhonov, A.
N. (1996) Curr. Topics Biophys., 20, 25-30.
49.Magnitsky, S. G., and Tikhonov, A. N. (1998)
Biofizika, 43, 69-76.
50.Trubitsin, B. V., and Tikhonov, A. N. (2003)
J. Magn. Reson., 163, 257-269.
51.Sigalat, C., de Kouchkovsky, Y., Haraux, F., and
de Kouchkovsky, F. (1988) Biochim. Biophys. Acta, 934,
375-388.
52.Magnitsky, S. G., and Tikhonov, A. N. (1995)
Biofizika, 40, 347-353.
53.Ewy, R. G., and Dilley, R. A. (2000) Plant
Physiol., 122, 583-595.
54.Williams, R. J. P. (1961) J. Theor. Biol.,
1, 1-17.
55.Williams, R. J. P. (1988) Ann. Rev. Biophys.
Chem., 17, 71-97.
56.Williams, R. J. P. (1978) FEBS Lett.,
85, 9-19.
57.Williams, R. J. P. (1993) Biosci. Rep.,
13, 191-212.
58.Westerhoff, H. V., Melandri, B. A., Venturoli,
G., Azzone, G. F., and Kell, D. B. (1984) Biochim. Biophys.
Acta, 768, 257-292.
59.Ferguson, S. J. (1985) Biochim. Biophys.
Acta, 811, 47-95.
60.Kell, D. B. (1979) Biochim. Biophys. Acta,
549, 55-99.
61.Haraux, F., and de Kouchkovsky, Y. (1983)
Physiol. Veg., 21, 563-576.
62.Yaguzhinsky, L. S., Krasinskaya, I. P., and
Dragunova, S. P. (1984) FEBS Lett., 167, 176-180.
63.Sigalat, C., Haraux, F., de Kouchkovsky, F.,
Hung, S., and de Kouchkovsky, Y. (1985) Biochim. Biophys. Acta,
809, 403-413.
64.Dilley, R. A., Theg, S. M., and Beard, W. A.
(1987) Annu. Rev. Plant Physiol., 37, 348-389.
65.Dilley, R. A. (2004) Photosynth. Res.,
80, 245-263.
66.Mulkidjanian, A. Y., Heberle, J., and Cherepanov,
D. A. (2006) Biochim. Biophys. Acta, 1757, 913-930.
67.Tikhonov, A. N., and Blumenfeld, L. A. (1985)
Biofizika, 30, 527-537.
68.Tikhonov, A. N., and Blumenfeld, L. A. (1990)
Zh. Fiz. Khim., 64, 1729-1740.
69.Blumenfeld, L. A., Grosberg, A. Yu., and
Tikhonov, A. N. (1991) J. Chem. Phys., 95, 7541-7547.
70.Tikhonov, A. N., and Shevyakova, A. V. (1985)
Biol. Membr. (Moscow), 2, 776-788.
71.Masarova, M., and Tikhonov, A. N. (1988)
Biofizika, 33, 889-891.
72.Haraux, F., and de Kouchkovsky, Y. (1980)
Biochim. Biophys. Acta, 592, 158-168.
73.Lolkema, J. S., Hellingwerf, K. J., and Konings,
W. N. (1982) Biochim. Biophys. Acta, 681, 85-94.
74.Hope, A. B., and Matthews, D. B. (1985) Aust.
J. Plant Physiol., 12, 9-19.
75.De Wolf, F. A., Groen, B. H., van Houte, L. P.
A., Peters, F. A. L. J., Krab, K., and Kraayenhof, R. (1985)
Biochim. Biophys. Acta, 809, 204-214.
76.Grzesiek, S., and Dencher, N. A. (1988)
Biochim. Biophys. Acta, 938, 411-424.
77.Auslander, W., and Junge, W. (1974) Biochim.
Biophys. Acta, 357, 285-298.
78.Junge, W., Auslander, W., McGeer, A. J., and
Runge, T. (1979) Biochim. Biophys. Acta, 346,
121-141.
79.Pick, U., and Avron, M. (1976) FEBS Lett.,
65, 348-353.
80.Witt, H. T. (1979) Biochim. Biophys. Acta,
505, 355-427.
81.Hong, Y. Q., and Junge, W. (1983) Biochim.
Biophys. Acta, 722, 197-208.
82.Tauber, M., Rogner, M., and Berry, S. (2001)
Biochim. Biophys. Acta, 1506, 31-46.
83.Kalas, T., and Dahlquist, F. W. (1980)
Biochemistry, 20, 5900-5907.
84.Ogawa, S., Shen, C., and Caqstillo, C. L. A.
(1980) Biochim. Biophys. Acta, 590, 159-161.
85.Nicolay, K., Lolkema, J., Hellingwert, K. J.,
Kaptein, R., and Konings, W. N. (1981) FEBS Lett., 123,
319-329.
86.Roberts, J. K. M., and Jardetzky, O. (1981)
Biochim. Biophys. Acta, 639, 53-76.
87.Foyer, C., Walker, D., Spencer, C., and Mann, B.
(1982) Biochem. J., 202, 429-434.
88.Tsien, R. Y. (1998) Annu. Rev. Biochem.,
67, 509-544.
89.Chudakov, D. M., Matz, M. V., Lukyanov, S., and
Lukyanov, K. A. (2010) Physiol. Rev., 90, 1103-1163.
90.Abad, M. F. C., Di Benedetto, G., Magalhaes, P.
J., Filippin, L., and Pozzan, T. (2004) J. Biol. Chem.,
279, 11521-11529.
91.Quintanihla, A. T., and Mehlholrn, R. J. (1978)
FEBS Lett., 91, 161-165.
92.Cafiso, D. S., and Hubbel, W. L. (1978)
Biochemistry, 17, 3871-3877.
93.Melandri, B. A., Mehlhorn, R. J., and Packer, L.
(1984) Arch. Biochem. Biophys., 235, 97-105.
94.Tikhonov, A. N., and Subczynski, W. K. (2005) in
Biological Magnetic Resonance, Vol. 23. Biomedical EPR
– Part A: Free Radicals, Metals, Medicine, and Physiology
(Eaton, S. S., Eaton, G. R., and Berliner, L. J., eds.) Kluwer
Academic/Plenum Publishers, New York-Boston-Dordrecht-London-Moscow,
pp. 147-194.
95.Ptushenko, V. V., Ikryannikova, L.
N., Grigor’ev, I. A., Kirilyuk, I. A., Trubitsin, B. V., and
Tikhonov, A. N. (2006) Appl. Magnet. Reson., 30,
329-343.
96.Ikryannikova, L. N., Ustynyuk, L. Yu., and
Tikhonov, A. N. (2004) J. Phys. Chem. A, 108,
4759-4768.
97.Tikhonov, A. N., Agafonov, R. V.,
Grigor’ev, I. A., Kirilyuk, I. A., Ptushenko, V. V., and
Trubitsin, B. V. (2008) Biochim. Biophys. Acta, 1777,
285-294.
98.Khramtsov, V. V., Weiner, L. M., Grigor’ev,
I. A., and Volodarsky, L. B. (1982) Chem. Phys. Lett.,
91, 69-72.
99.Khramtsov, V. V., and Volodarsky, L. B. (1998) in
Biological Magnetic Resonance, Vol. 14 (Berliner, L. J., ed.)
Plenum Press, New York-London, pp. 109-180.
100.Kirilyuk, I. A., Bobko, A. A., Khramtsov, V.
V., and Grigor’ev, I. A. (2005) Org. Biomol. Chem.,
3, 1269-1274.
101.Kocherginski, N., and Swartz, H. M. (1995)
Nitroxide Spin Labels: Reactions in Biology and Chemistry, CRC
Press, Boca Raton-New York-London-Tokyo.
102.Tikhonov, A. N., Khomutov, G. B., and Ruuge, E.
K. (1984) Photobiochem. Photobiophys., 8, 261-269.
103.Zito, F., Finazzi, G., Joliot, P., and Wollman,
F.-A. (1998) Biochemistry, 37, 10395-10403.
104.Stock, D., Leslie, A. G. W., and Walker, J. E.
(1999) Science, 286, 1700-1705.
105.Seelert, H., Poetsch, A., Dencher, N. A.,
Engel, A., Stahlberg, H., and Mulle, D. J. (2000) Nature,
405, 418-419.
106.Pogoryelov, D., Yu, J., Meier, T., Vonck, J.,
Dimroth, P., and Muller, D. J. (2005) EMBO Repts., 6,
1040-1044.
107.Pogoryelov, D., Reichen, C., Klyszejko, A. L.,
Brunisholz, R., Muller, D. J., Dimroth, P., and Meier, T. (2007) J.
Bacteriol., 189, 5895-5902.
108.Vollmar, M., Schlieper, D., Winn, M., Buchner,
C., and Groth, G. (2009) J. Biol. Chem., 284,
18228-18235.
109.Krah, A., Pogoryelov, D., Meier, T., and
Faraldo-Gomez, J. D. (2010) J. Mol. Biol., 395,
20-27.
110.Watt, I. N., Montgomery, M. G., Runswick, M.
J., Leslie, A. G. W., and Walker, J. E. (2010) Proc. Natl. Acad.
Sci. USA, 107, 16823-16827.
111.Assadi-Porter, F. M., and Fillingame, R. H.
(1995) Biochemistry, 34, 16186-16194.
112.Valiyaveetil, F. I., and Fillingame, R. H.
(1997) J. Biol. Chem., 272, 32635-32641.
113.Long, J. C., Wang, S., and Vik, S. B. (1998)
J. Biol. Chem., 273, 16235-16240.
114.Jones, P. C., Hermolin, J., Jiang, W., and
Fillingame, R. H. (2000) J. Biol. Chem., 275,
31340-31346.
115.Diez, M., Zimmermann, B., Borsch, M., Konig,
M., Schweinberger, E., Steigmiller, S., Reuter, R., Felekyan, S.,
Kudryavtsev, V., Seidel, C. A., and Graber, P. (2004) Nat. Struct.
Mol. Biol., 11, 135-141.
116.Sambongi, Y., Iko, Y., Tanabe, M., Omote, H.,
Iwamoto-Kihara, A., Ueda I., Yanagida, T., Wada, Y., and Futai, M.
(1999) Science, 286, 1722-1724.
117.Panke, O., Gumbiowski, K., Junge, W., and
Engelbrecht, S. (2000) FEBS Lett., 472, 34-38.
118.Nishio, K., Iwamoto-Kihara, A., Yamamoto, A.,
Wada, Y., and Futai, M. (2002) Proc. Natl. Acad. Sci. USA,
99, 13448-13452.
119.Cherepanov, D., Mulkidjanian, A. Y., and Junge,
W. (1999) FEBS Lett., 449, 1-6.
120.Junge, W., Lill, H., and Engelbrecht, S. (1997)
Trends Biochem. Sci., 22, 420-423.
121.Oster, G., and Wang, H. (2000) Biochim.
Biophys. Acta, 1458, 482-510.
122.Oster, G., and Wang, H. (2003) Trends Cell
Biol., 13, 114-121.
123.Boyer, P. D. (1993) Biochim. Biophys.
Acta, 1140, 215-250.
124.Boyer, P. D. (1997) Annu. Rev. Biochem.,
66, 717-749.
125.Weber, J., and Senior, A. E. (1997) Biochim.
Biophys. Acta, 1319, 19-58.
126.Vinogradov, A. D. (2000) J. Exp. Biol.,
203, 41-49.
127.Romanovsky, Yu. M., and Tikhonov, A. N. (2010)
Usp. Fiz. Nauk, 180, 931-956.
128.Biochim. Biophys. Acta (2000),
1458, No. 2-3 (Special Issue, Guest, Walker, J., ed.).
129.J. Bioenerg. Biomembr. (2000),
32, No. 4-5 (Minireview series, ATP synthesis in the Year 2000:
current views about structure, motor components, energy
interconversions and catalytic mechanisms, Pt. I and II).
130.J. Exp. Biol. (2000) 203(1),
(Special issue, Harvey, W. R., Boutilier, R. G., and Nelson, N.,
eds.).
131.Edsall, J. T., and Gutfreund, H. (1983)
Biothermodynamics. The Study of Biochemical Processes at
Equilibrium, Wiley, Chichester.
132.Junge, W., Panke, O., Cherepanov, D. A.,
Gumbiowski, K., Muller, M., and Engelbrecht, S. (2001) FEBS
Lett., 504, 152-160.
133.Sun, S., Chandler, D., Dinner, A. R., and
Oster, G. (2003) Eur. Biophys. J., 32, 676-683.
134.Junge, W., Sielaff, H., and Engelbrecht, S.
(2009) Nature, 459, 364-370.
135.Sabbert, D., Engelbrecht, S., and Junge, W.
(1996) Nature, 381, 623-625.
136.Noji, H., Yasuda, R., Yoshida, M., and
Kinosita, K. (1997) Nature, 386, 299-302.
137.Heldt, H. W., Werdan, K., Milivancev, M., and
Geller, G. (1973) Biochim. Biophys. Acta, 314,
224-241.
138.Robinson, S. P. (1985) Biochim. Biophys.
Acta, 806, 187-194.
139.Alberty, R. A. (1969) J. Biol. Chem.,
244, 3290-3302.
140.Rosing, J., and Slater, E. C. (1972)
Biochim. Biophys. Acta, 267, 275-290.
141.Panke, O., and Rumberg, B. (1997) Biochim.
Biophys. Acta, 1322, 183-194.
142.Turina, P., Samoray, D., and Graber, P. (2003)
EMBO J., 22, 418-426.
143.Steigmiller, S., Turina, P., and Graber, P.
(2008) Proc. Natl. Acad. Sci. USA, 105, 3745-3750.
144.Haraux, F., and de Kouchkovsky, Y. (1998)
Photosynth. Res., 57, 231-251.
145.Tomashek, J. J., and Brusilov, W. S. A. (2000)
J. Bioenerg. Biomembr., 32, 493-500.
146.Van Walraven, H. S., Strotmann, H., Schwarz,
O., and Rumberg, B. (1996) FEBS Lett., 379, 309-313.
147.Giersch, C., Heber, U., Kobayashi, Y., Inoue,
Y., Shibata, K., and Heldt, H. W. (1980) Biochim. Biophys. Acta,
590, 59-73.
148.Cruz, J. A., Avenson, T. J., Kanazawa, A.,
Takizawa, K., Edwards, G. E., and Kramer, D. M. (2007) J. Exp.
Botany, 56, 395-406.
149.Li, Z., Wakao, S., Fischer, B. B., and Niyogi,
K. K. (2009) Annu. Rev. Plant Biol., 60, 239-260.
150.Buchanan, B. B. (1991) Arch. Biochem.
Biophys., 288, 1-9.
151.Woodrow, I. E., and Berry, J. A. (1988)
Annu. Rev. Plant Physiol. Plant Mol. Biol., 39,
533-594.
152.Allen, J. F. (2003) Trends Plant Sci.,
8, 15-19.
153.Minagawa, J. (2011) Biochim. Biophys.
Acta, 1807, 897-905.
154.Kuvykin, I. V., Ptushenko, V. V., Vershubskii,
A. V., and Tikhonov, A. N. (2011) Biochim. Biophys. Acta,
1807, 336-347.
155.Kautsky, H., and Hirsch, A. (1931)
Naturwissenschaften, 19, 964-964.
156.Edwards, G., and Walker, D. A. (1983)
C3, C4: Mechanisms, and Cellular and
Environmental Regulation of Photosynthesis, Blackwell, Oxford.
157.Ort, D. R., and Osborough, K. (1992) Annu.
Rev. Plant Physiol. Plant Mol. Biol., 43, 269-291.
158.Govindjee (1995) Aust. J. Plant
Physiol., 22, 131-160.
159.Carmeli, C., and Lifshitz, Y. (1972)
Biochim. Biophys. Acta, 267, 86-95.
160.Bakker-Grunwald, T., and van Dam, K. (1974)
Biochim. Biophys. Acta, 347, 290-298.
161.Mills, J. D., and Mitchell, P. (1984)
Biochim. Biophys. Acta, 764, 93-104.
162.Junesch, U., and Graber, P. (1987) Biochim.
Biophys. Acta, 893, 275-288.
163.Mills, J. D., and Hind, G. (1979) Biochim.
Biophys. Acta, 547, 455-462.
164.Mills, J. D., and Mitchell, P. (1982)
Biochim. Biophys. Acta, 679, 75-82.
165.He, X., Miginiac-Maslow, M., Sigalat, C.,
Keryer, E., and Haraux, F. (2000) J. Biol. Chem., 275,
13250-13258.
166.Bald, D., Noji, H., Yoshida, M., Hirono-Hara,
Y., and Hisabori, T. (2001) J. Biol. Chem., 276,
39505-39507.
167.Kramer, D. M., and Crofts, A. R. (1989)
Biochim. Biophys. Acta, 976, 28-41.
168.Kramer, D. M., Wise, R. R., Frederick, J. R.,
Alm, D. M., Hesketh, J. D., Ort, D. A., and Crofts, A. R. (1990)
Photosynth. Res., 26, 213-222.
169.Selman-Reimer, S., Duhe, R. J., Stockman, B.
J., and Selman, B. R. (1991) J. Biol. Chem., 266,
182-188.
170.Konno, H., Murakami-Fuse, T., Fujii, F.,
Koyama, F., Ueoka-Nakanishi, H., Pack, C.-G., Kinjo, M., and Hisabori,
T. (2006) EMBO J., 25, 4596-4604.
171.Cingolani, G., and Duncan, T. M. (2010)
Nature Struct. Mol. Biol., 18, 701-708.