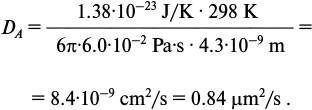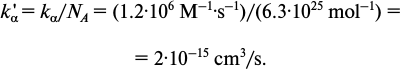Equal Impact of Diffusion and DNA Binding Rates on the Potential Spatial Distribution of Nuclear Factor κB Transcription Factor inside the Nucleus
A. M. Sycheva1, A. Kel2,3, E. N. Nikolaev1,4, and S. A. Moshkovskii1*
1Orekhovich Institute of Biomedical Chemistry, Russian Academy of Medical Sciences, ul. Pogodinskaya 10, 119121 Moscow, Russia; E-mail: smosh@mail.ru2GeneXplain GmbH, Am Exer 10 b, D-38302, Wolfenbuttel, Germany
3Institute of Chemical Biology and Fundamental Medicine, Russian Academy of Sciences, pr. Akademika Lavrentieva 10, 630090 Novosibirsk, Russia
4Emanuel Institute of Biochemical Physics, Russian Academy of Sciences, ul. Kosygina 4, 119334 Moscow, Russia
* To whom correspondence should be addressed.
Received February 16, 2014; Revision received March 5, 2014
There are two physical processes that influence the spatial distribution of transcription factor molecules entering the nucleus of a eukaryotic cell, the binding to genomic DNA and the diffusion throughout the nuclear volume. Comparison of the DNA–protein association rate constant and the protein diffusion constant may determine which one is the limiting factor. If the process is diffusion-limited, transcription factor molecules are captured by DNA before their even distribution in the nuclear volume. Otherwise, if the reaction rate is limiting, these molecules diffuse evenly and then find their binding sites. Using well-studied human NF-κB dimer as an example, we calculated its diffusion constant using the Debye–Smoluchowski equation. The value of diffusion constant was about 10–15 cm3/s, and it was comparable to the NF-κB association rate constant for DNA binding known from previous studies. Thus, both diffusion and DNA binding play an equally important role in NF-κB spatial distribution. The importance of genome 3D-structure in gene expression regulation and possible dependence of gene expression on the local concentration of open chromatin can be hypothesized from our theoretical estimate.
KEY WORDS: transcription factor, nuclear factor κB, diffusion, rate constant, DNA–protein interactionDOI: 10.1134/S0006297914060121
Abbreviations: NF-κB, nuclear factor κB (nuclear factor kappa-light-chain-enhancer of activated B cells); TF, transcription factor.
To fulfill their cell functions, transcription factors (TF) and other
DNA binding proteins have to migrate throughout the nucleus in
eukaryotes or the cell in prokaryotes and find their specific binding
site on a DNA strand. It is well known that many such proteins easily
bind not only to their specific DNA motif, but also to a nonspecific
DNA. Thus, it was predicted [1] and then shown
in vivo that E. coli lac-repressor is bound to DNA
during 90% of its lifetime [2]. Similar results
were achieved in the case of some human DNA binding proteins; most of
these molecules were also maintained in bound state on chromatin [3].
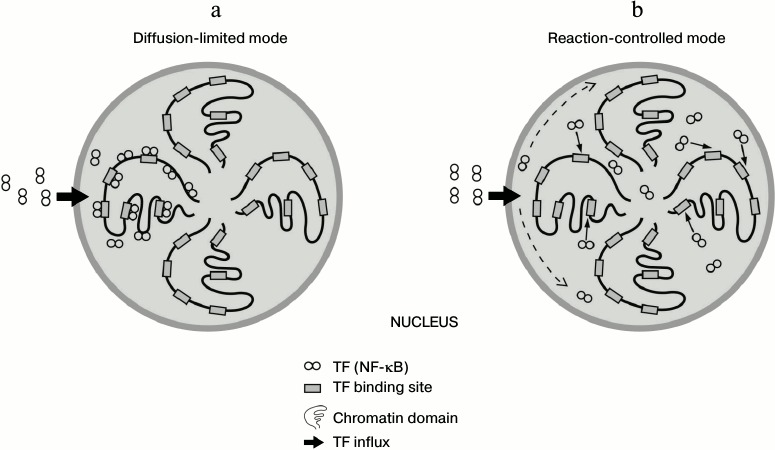
Due to the fast and sufficient affinity of binding of TF to nonspecific DNA, the question arises whether association of TFs to DNA occurs more promptly than their diffusion-driven distribution throughout the nucleus. If so, the nuclear distribution of proteins will not be homogenous, i.e. TF molecules will be fixed on DNA sites close to the nuclear pores through which they have entered the nucleus (diffusion-limited mode) [4] (figure, panel (a)). Otherwise, if the diffusion of TFs is faster than binding to DNA, protein molecules will find their binding sites after even distribution inside the nucleus (reaction-limited mode) [4] (figure, panel (b)). It is of great interest to calculate using a great deal of biochemical data on specific human TFs what scenario of the two is more appropriate (figure). A recent study has disclosed using next generation sequencing that the human genome is organized in 3D space as a fractal-like structure [5]. If the spatial structure of chromosomes is highly determined and not stochastic, the existence of spatial factor in TF functioning and overall gene expression mechanisms can be assumed.
Schematic representation of alternative modes for spatial distribution of transcription factor NF-κB inside the nucleus. a) Diffusion is limiting and protein molecules quickly adhere to open chromatin domains. b) Transcription factor molecules are evenly distributed throughout the nucleoplasm and then find their binding sites on the open chromatin. According to our calculation, the scenario is intermediate between these two cases, and transcription factor behavior may be partly limited by diffusion and also depend on the local concentration of open chromatin
Here we made a theoretical estimate of which of two processes – diffusion or DNA binding – limits the distribution of TF throughout the nucleus using human NF-κB as an example. NF-κB is a crucial transcriptional factor involved in inflammation, immunity, cell differentiation, and cell growth, as well as in cancer. It acts as a homo- or heterodimer combined of p65 (RelA), p50, c-Rel, RelB, and p52 protein subunits [6]. NF-κB p65-p50 heterodimer is the most abundant species of NF-κB complexes and it is the molecule that we mean as NF-κB in this report. NF-κB dimer binds to 9-11-bp κB sites of promoter and enhancer regions of its target genes.
To predict the mode of NF-κB distribution in the nucleus, the data by Bergkvist et al. [7] was used where kinetics of p65-p50 dimer binding to DNA was disclosed. In those experiments a DNA fragment was anchored on a surface plasmon resonance chip, and a protein-binding site at the DNA can therefore be conceived as an immobile sphere. This approximation can be further used for describing TF binding sites in the cell, where a single binding site represents a part of a huge DNA molecule, which is substantially less mobile than a TF molecule. Then consider a protein as a mobile sphere that is moving across the nucleus as a result of 3D diffusion.
According to the Debye–Smoluchowski equation [4], the upper limit of the rate constant for a diffusion-controlled reaction is calculated by the formula:
where DA and DB are diffusion coefficients of protein and DNA, respectively; rA + rB is a reaction radius; f is a factor that takes into account electrostatic interaction.
If the DNA is fixed in space according to our model, then DB = 0. At the same time, the diffusion coefficient of TF is calculated by the Stokes–Einstein equation,
where r is the hydrodynamic radius of the protein and η is the dynamic viscosity of the solution, i.e. the nucleoplasm. The hydrodynamic radius of NF-κB p65-p50 dimer can be approximately estimated as 4.3 nm as compared to such radius of hexokinase enzyme with molecular weight of 102 kDa [8]. The nucleoplasm dynamic viscosity as measured in vivo is about 4-8 cP [9, 10]. Thus, for the calculation we can use a viscosity value of 6 cP, i.e. 6·10−2 Pa·s. Substitute the estimated values in Eq. (2):
Take the reaction radius rA + rB to be 0.5 nm [11]. In the nucleus, the f coefficient of Eq. (2) can be considered to be 1 due to the high ionic strength, which minimizes the electrostatic component in a reaction between molecules. Then,
Using the viscosity value as published [9, 10] and Eq. (1) that connects diffusion coefficient with viscosity, we should keep in mind that the calculation is made on the assumption that a nucleoplasm is a homogeneous liquid and diffusion takes place homogeneously in space. Correspondingly, we calculate the lower limit for the diffusionally determined part of the rate constant. In general, macromolecular structures in the cellular space make diffusion of smaller molecules faster, because these structures serve as channels that facilitate migration by the reduction of space dimensionality. However, in case of chromatin, the situation may be different if we suggest that protein complex is sliding along a DNA strand. Very coiled DNA domains may apparently retain TF migration, despite fast linear diffusion of protein complexes sliding along the DNA strand. For example, it takes about 55 min for p53 tumor suppressor with linear diffusion coefficient of 1.4⋅106 bp2/s [12] to run over a short distance of 100,000 bp.
The next step is to estimate the rate constant for the DNA–TF reaction. The rate constant for the association of TFs with their binding sites on DNA strand is in the range between 106 and 107 M–1·s–1 depending on the considered transcription factor [6, 13, 14]. As proposed earlier, the value of the association rate constant for TF binding to nonspecific DNA does not exceed this value [13]. As measured before, NF-κB binds to its specific DNA site with rate constant ka = 1.2·106 M–1·s–1 [14].
Let us recalculate the ka and compare it with the diffusion constant kSmol computed before:
Thus, NF-κB dimer rate constants for diffusion and for binding to specific DNA are substantially the same, and therefore neither of these processes can be critically limiting. In the nucleus, substantially equal contribution of diffusion and DNA binding can be expected, and this may lead us to important speculations.
First, as DNA binding can occur at a rate close to the diffusion rate, a spatial factor may play important role when TF molecules enter the nucleus. In other words, if a long distance inside the nucleus spans between such molecules and their open binding sites, TFs may never reach this place being in a maze of closely located open chromatin domains. The hypothesis about possible polarity and nonhomogeneity of the nuclear envelope in the context of macromolecular transport is in good correspondence with the background of chromosome territories and 3D-genome organization [15, 16].
Moreover, a population of TF molecules entered into the nucleus may be entrapped by the chromatin if the local concentration of open binding sites on DNA is sufficient. In this context, the spatial organization of gene transcription is of high interest. Coexpressed genes regulated by the same TF are expected to be brought together spatially. This phenomenon is already observed on the level of neighboring genes [17], but it should be studied on the genome-wide scale [18].
Thus, spatial aspects of gene expression are waiting experimental deciphering, which is important for understanding of cell division, differentiation, molecular cancer, and other crucial cell functions. In this field, protein (e.g. TF) mobility map studies [19] should meet high-throughput genomic experiments of gene expression and TF distribution [20].
The model that is used for this communication is very simplified. Important areas that consider the tiny chromatin structure and regulation, molecular dynamics of TF and their competition for binding sites, their regulation by cofactors, etc. are out of the scope of the model. Nevertheless, even such a simplified approach makes us believe that the regulation of transcription by TF can be limited not only by reaction between TFs and DNA, but also by diffusion of these proteins inside the nucleus.
The authors thank Ms. Lidia Semenikhina for her kind help in figure preparation.
This work was funded by the program of basic research of the Russian Academy of Medical Sciences.
REFERENCES
1.Kao-Huang, Y., Revzin, A., Butler, A. P.,
O’Conner, P., Noble, D. W., and von Hippel, P. H. (1977) Proc.
Natl. Acad. Sci. USA, 74, 4228-4232.
2.Elf, J., Li, G.-W., and Xie, X. S. (2007)
Science, 316, 1191-1194.
3.Phair, R. D., Scaffidi, P., Elbi, C., Vecerova, J.,
Dey, A., Ozato, K., Brown, D. T., Hager, G., Bustin, M., and Misteli,
T. (2004) Mol. Cell. Biol., 24, 6393-6402.
4.Berg, O. G., and von Hippel, P. H. (1985) Annu.
Rev. Biophys. Biophys. Chem., 14, 131-160.
5.Lieberman-Aiden, E., van Berkum, N. L., Williams,
L., Imakaev, M., Ragoczy, T., Telling, A., Amit, I., Lajoie, B. R.,
Sabo, P. J., Dorschner, M. O., Sandstrom, R., Bernstein, B., Bender, M.
A., Groudine, M., Gnirke, A., Stamatoyannopoulos, J., Mirny, L. A.,
Lander, E. S., and Dekker, J. (2009) Science, 326,
289-293.
6.Natoli, G., Saccani, S., Bosisio, D., and Marazzi,
I. (2005) Nat. Immunol., 6, 439-445.
7.Bergqvist, S., Alverdi, V., Mengel, B., Hoffmann,
A., Ghosh, G., and Komives, E. A. (2009) Proc. Natl. Acad. Sci.
USA, 106, 19328-19333.
8.Case, F., and Alexandridis, P. (2003) Mesoscale
Phenomena in Fluid Systems, American Chemical Society, Washington,
DC.
9.Seksek, O., Biwersi, J., and Verkman, A. S. (1997)
J. Cell Biol., 138, 131-142.
10.Siebrasse, J. P., Veith, R., Dobay, A.,
Leonhardt, H., Daneholt, B., and Kubitscheck, U. (2008) Proc. Natl.
Acad. Sci. USA, 105, 20291-20296.
11.Riggs, A. D., Bourgeois, S., and Cohn, M.
(1970) J. Mol. Biol., 53, 401-417.
12.Tafvizi, A., Huang, F., Fersht, A. R., Mirny, L.
A., and van Oijen, A. M. (2011) Proc. Natl. Acad. Sci. USA,
108, 563-568.
13.Vukojevic, V., Papadopoulos, D. K., Terenius, L.,
Gehring, W. J., and Rigler, R. (2010) Proc. Natl. Acad. Sci.
USA, 107, 4093-4098.
14.Babayeva, N. D., Wilder, P. J., Shiina, M., Mino,
K., Desler, M., Ogata, K., Rizzino, A., and Tahirov, T. H. (2010)
Cell Cycle, 9, 3054-3062.
15.Bolzer, A., Kreth, G., Solovei, I., Koehler, D.,
Saracoglu, K., Fauth, C., Muller, S., Eils, R., Cremer, C., Speicher,
M. R., and Cremer, T. (2005) PLoS Biol., 3, e157.
16.Marti-Renom, M. A., and Mirny, L. A. (2011)
PLoS Comput. Biol., 7, e1002125.
17.Michalak, P. (2008) Genomics, 91,
243-248.
18.Khrameeva, E. E., Mironov, A. A., Fedonin, G. G.,
Khaitovich, P., and Gelfand, M. S. (2012) PLoS One, 7,
e33947.
19.Erdel, F., Muller-Ott, K., Baum, M., Wachsmuth,
M., and Rippe K. (2011) Chromosome Res., 19, 99-115.
20.Mokry, M., Hatzis, P., Schuijers, J., Lansu, N.,
Ruzius, F. P., Clevers, H., and Cuppen, E. (2012) Nucleic Acids
Res., 40, 148-158.