REVIEW: Is It Possible to Prove the Existence of an Aging Program by Quantitative Analysis of Mortality Dynamics?
G. A. Shilovsky1,2*, T. S. Putyatina2, S. N. Lysenkov2,3, V. V. Ashapkin1, O. S. Luchkina4, A. V. Markov2, and V. P. Skulachev1
1Lomonosov Moscow State University, Belozersky Institute of Physico-Chemical Biology, 119991 Moscow, Russia; E-mail: gregory_sh@list.ru, grgerontol@gmail.com2Lomonosov Moscow State University, Faculty of Biology, 119991 Moscow, Russia
3Russian Clinical Research Center for Gerontology, 129226 Moscow, Russia
4Severtsov Institute of Ecology and Evolution, Russian Academy of Sciences, 119071 Moscow, Russia
* To whom correspondence should be addressed.
Received September 16, 2016
Accumulation of various types of lesions in the course of aging increases an organism’s vulnerability and results in a monotonous elevation of mortality rate, irrespective of the position of a species on the evolutionary tree. Stroustrup et al. (Nature, 530, 103-107) [1] showed in 2016 that in the nematode Caenorhabditis elegans, longevity-altering factors (e.g. oxidative stress, temperature, or diet) do not change the shape of the survival curve, but either stretch or shrink it along the time axis, which the authors attributed to the existence of an “aging program”. Modification of the accelerated failure time model by Stroustrup et al. uses temporal scaling as a basic approach for distinguishing between quantitative and qualitative changes in aging dynamics. Thus we analyzed data on the effects of various longevity-increasing genetic manipulations in flies, worms, and mice and used several models to choose a theory that would best fit the experimental results. The possibility to identify the moment of switch from a mortality-governing pathway to some other pathways might be useful for testing geroprotective drugs. In this work, we discuss this and other aspects of temporal scaling.
KEY WORDS: lifespan, aging, survival curves, temporal scaling, phenoptosisDOI: 10.1134/S0006297916120075
Abbreviations: AFT model, accelerated failure time model; AMPK, AMP-activated protein kinase; CV, coefficient of variation; FI, frailty index; HIF-1, hypoxia-inducible factor 1; PH model, Cox proportional hazards model; SOD, superoxide dismutase; tBuOOH, tert-butyl hydroperoxide.
Aging is associated with the emergence of age-related diseases,
senility, and deterioration of the organism. These manifestations
increase the risk of mortality (number of individuals dying within a
certain period). All attempts to harmoniously unite aging and mortality
in a single theory have been unsuccessful, due probably to insufficient
understanding of the process of biological aging. It remains obscure
how age-related disorders lead to death.
One of the reasons for the development of age-related disorders and appearance of phenotypical traits of aging might be accumulation of unrepaired genomic lesions caused by increased production of reactive oxygen species and decreased efficiency of DNA repair and antioxidant protective systems. This should make an individual more vulnerable with age and elevate the mortality rate in multicellular organisms, irrespectively of their position on the evolutionary tree.
Individual longevity varies from specimen to specimen. Even genetically similar or identical organisms (e.g. queens and workers of social insects) can display different survival curves. Despite common opinion that evolution inevitably leads to the age-related increase in mortality and decrease in fertility in mature organisms, different species have very different mortality dynamics (mortality curves could be upward, flat, downward, concave, or convex in both long- and short-lived species) [2]. Existing theoretical approaches do not explain why aging has developed in some species, but not in others [3].
One of the authors of the present work (V.P.S.), who noted this contradiction, proposed the concept of acute and chronic phenoptosis [4], which postulates an existence of the programmed death of organisms, i.e. death caused by initiation of a genetic program for self-elimination. This concept allows uniting the hypothesis of Weismann on aging as an adaptive mechanism of programmed death with an alternative point of view that aging is a result of accumulation of errors and lesions in an organism [4, 5] (see “Evolution” below).
In this work, we analyzed data on the effects of various longevity-increasing genetic manipulations in flies, worms, and mice and used several models to choose a theory that would best fit the experimental results.
EVOLUTION
There is no doubt that aging is a subject of evolution, although exact mechanisms of this process remain undeciphered [6-8]. The main argument against aging because of adaptive evolution is that after the fertility peak, the pressure of natural selection gravitates to zero, and only stochastic decrease in functionality continues [6, 9-11]. If at reproductive age harmful mutations tend to be selected against because of their negative contribution to adaptation (production of offspring), similar mutations manifested at older age will be relatively neutral, since their bearers have been already excluded from reproduction.
In reality, in many animals traits that have been acquired in the post-reproductive period and turned out to be beneficial for a population are transferred through learning to individuals still capable of reproduction, and this will increase their adaptability, as well as resistance of the whole population, to environmental factors. And natural selection is nothing else but preferential reproduction of the fittest [12]. In social animals, the older generation teaches, first of all, its own offspring. The longer this older generation lives, the more knowledge it will pass to youngsters (their own descendants), some of which will possess longevity genes. For example, only 3-4 ants out of a million have a chance to reproduce (and they leave their nest maybe only once in a lifetime), but this does not prevent ants from evolving and adapting to new conditions such as anthropogenic factors [13]. This mechanism works for animals that are capable of learning and that live in multigenerational groups [14] – mammals, many social insects, birds, and some other species.
Natural selection is undoubtedly a strictly individual process. However, organismal traits correlate with each other, and genes are pleiotropic [12]. Therefore, the presence of longevity genes might correlate with some adaptive trait, and because of it, these genes will be preserved in a population. Hence, we agree with researchers who state that aging can be a result of positive selection [15].
Williams, who based his theory of aging on pleiotropy, postulated the existence of genes that increase the reproductive success at young age despite negative effects delayed to old age (antagonistic pleiotropy) [16]. Mutations in these gene increase longevity by decreasing fertility [17]. This hypothesis was confirmed by the phenomenon of proliferating cell senescence (irreversible inhibition of cell division due to cell damage) that increases an organism’s viability at younger age by lowering the risk of cancer development, but decreases lifespan due to accumulation of senescent cells [18]. Another similar hypothesis – the disposable soma theory – suggests the existence of genes that control redistribution of energy resources between somatic cells and the reproductive system (i.e. postulates competition between somatic maintenance and reproduction) [8]. For example, in small nonpredatory animals, spending most energy for rapid reproduction at the expense of somatic maintenance will be an efficient strategy under unfavorable environmental conditions. This pattern of resource distribution could change only upon decrease in the environmental pressure. Thus, the lifespans of opossums in a population that by accident inhabited an isolated island were longer than of their “mainland” counterparts [19]. Physiological aging (determined from the collagen structure in tail tendons) was also slowed in the island-dwelling animals.
If the evolution of aging is possible, a special aging program might exist as well. Because lifespan is a stable specific trait, like body size and fertility, longevity (the age of death) and longevity-regulating mechanisms should be programmed in the genome at least partially [20, 21].
Weismann was the first to suggest that since non-aging organisms are harmful for the population because they take resources from the younger ones, evolution should lead to the origin of an aging program [22]. He believed that the biological mechanism of such a program will be limiting the number of somatic cell divisions (in contrast to infinitely proliferating germ line), and he explained the difference in lifespans among species by different numbers of cell generations.
Another “programmed longevity” theory is based on the existence of genes that promote an organism’s survival by repairing somatic cells [17]. This theory has been confirmed by a discovery of tens of mutations that increase longevity and modulate an organism’s stress resistance [23, 24]. An important role in this process belongs to epigenetic cell systems. Much experimental data indicate that aging is accompanied by certain epigenetic changes and, to a considerable extent, is regulated by these changes [25, 26]. A longevity program might have originated in evolution for adapting to short-termed extreme interventions (variations in temperature, humidity, or availability of food) [17, 23], but not in response to constant pressure of unfavorable environmental conditions (predators, diseases), as proposed by the theories of mutation accumulation and disposable soma.
The efficiency of artificial selection for increased lifespan [27] also indicates that longevity is encoded, at least partially, by the genome. The possibility of extending the lifespan of C. elegans worms almost two-fold by inactivating some of their genes, as demonstrated by Kenyon et al. [28], suggests the existence of a slow program leading to the organism’s death (chronic phenoptosis) [4].
It should be noted that such a program could function simultaneously with other known aging mechanisms, or even that these mechanisms are a part of the program. Therefore, Weismann’s hypothesis on aging as an adaptive mechanism of programmed death can be united with an alternative point of view that aging results from accumulation of errors and lesions [5]. Also, computer modeling demonstrated that under certain conditions sedentary organisms (plants and some animals) can develop acute rather than chronic phenoptosis, and this switch is evolutionarily beneficial [29].
Accumulation of lesions could be monitored by special systems that send a “death signal” for activating the phenoptotic program when damage reaches a critical level. The epigenome could be one such system that acts as a general sensor of cell dysfunction and responds to any changes in the state of the genome or internal environment, including changes associated with aging [26]. On the other hand, the epigenome actively regulates gene expression. Aging is accompanied by progressively increasing cell-to-cell variations in the levels of gene expression and activities of the corresponding physiological processes [30]. Perhaps these variations result in a gradual decline in tissue functions until the process reaches a critical level that leads to failure and induction of the phenoptotic program. In particular, the described processes are typical for genes encoding mitochondrial proteins involved in ATP synthesis. Also, septic shock is an example of a pathological condition with typical phenoptotic traits. Many of its properties indicate that rapid lethal outcome is orchestrated by the organism itself – when the organism suffers massive invasion of bacteria, fast death would prevent the spread of the epidemic. Sepsis is accompanied by massive release of apoptosis-inducing cytokines by macrophages [4].
Biological aging should be distinguished from chemical aging, i.e. one that is not programmed in the genome. The L→D isomerization of amino acids in crystalline of the whale eye lens is an example of chemical aging. In an eye of a 200-year-old whale, ~40% of L-aspartate is converted into its D-isomer, which negatively affects the properties of the crystalline, a protein that once synthesized stays in the lens for the whole whale’s lifetime. Other examples of non-programmed chemical aging are reactions of protein carbonylation and deamidation [4].
Studies of biological aging are hindered by the fact that in nature many animals die from random causes and do not survive until the time determined by the basic aging mechanism. Biological aging can be studied only in the laboratory, although in nature aging acts as a factor that increases the risk of death [6].
Until recently, mathematical models of aging have been based on the Gompertz law, i.e. on analysis of mortality dynamics in organismal cohorts [2, 31, 32]. For example, Jones et al. [2] comparatively analyzed age patterns of mortality, survival, and fertility for a broad range of taxa (23 vertebrates, 10 invertebrates, 12 vascular plants, and a brown alga). The samples were representative enough, but the authors’ conclusions were not indisputable; that is why we decided to discuss them in our paper [33]. We divided survival, mortality, and fertility curves (published by the Max Planck Institute for Demographic Research) [2] into four large groups according to the ratio of mortality at the terminal age to average mortality during the entire studied period, where group I included species with minimal changes in mortality with age, and group IV – species with the maximal changes.
In our opinion, the data presented by Jones et al. [2] do not reveal pronounced traits of the Gompertz type of aging in plants and algae. It has been stated many times that, in contrast to animals, aged plant cells are not accumulated but die via a programmed mechanism. Moreover, dead cells are not eliminated; they are incorporated into plant structures performing supporting and transport functions. Hence, we suggest that plants have learned to fight phenoptosis by implementing the cell death program.
The Gompertz type of aging is most typical for mammals and species with many postmitotic cells, e.g. insects. Considerable variations in the manifestation of the Gompertz type of aging can be seen in birds, from the Bali mynah to the great tit. Despite the conclusion of Jones et al., large birds also age, but their biological aging can begin to manifest itself at a rather late age that is reached by less than 5% of all specimens. The aging of small birds, which have numerous enemies and high exogenous mortality, is almost impossible to observe in nature, as predicted by Medawar [10].
Amphibians and reptiles belong to group I having flat mortality curves. Reptiles can live and remain capable of reproduction for an extremely long time, but the proportion of long-lived individuals among them is probably also no greater than 5% of the initial cohort. For this reason, their mortality dynamics could not be assessed by the method of Jones et al., who analyzed the dynamics of the studied parameters until the age to which only 5% of the cohort survived, which the authors called “terminal”.
In long-lived species with a less pronounced increase in mortality with age, as well as in animals of average lifespan that reach the terminal age earlier than they could have enough time to become senescent, the method of Jones et al. is capable of characterizing only a small part of the life cycle and does not allow judging how senescence manifests itself in late stages of the life cycle.
DEVELOPMENT OF NEW MODELS
Although the rate of aging varies among species, the effects of aging are remarkably consistent. On one hand, related species, such as mice and naked mole rats, can have average lifespans that differ more than tenfold. On the other hand, such evolutionary distant organisms as yeast and humans undergo similar molecular changes throughout aging [34]. Random factors cause great variations in individual lifespans even in homogenous populations [35, 36]. Studying this stochastic behavior might help to find a connection between aging and molecular mechanism that regulate longevity.
The semiparametric Cox proportional hazards (PH) model [37] is widely used in medicine and epidemiology, but to a considerably less extent in studies of longevity and aging. The model estimates the levels of age-dependent mortality under different conditions (hazard ratios). It is very useful in medicine, e.g. for estimating the risks of postoperative mortality. However, it is not intuitively convenient for analysis of aging, when results are presented in the form of survival curves [37]. The PH approach models hi(t), the hazard function for the ith individual at time t, as the product between the baseline hazard function h0(t) and the function that depends on coefficients β1,…, βp and explanatory variables x1,…, xp for the ith individual.
hi(t) = exp(β1x1i + β2x2i +…+ βpxpi)h0(t)
In the absence of covariates, only one variable x1 is included in the model to distinguish between control (0) and experimental treatments (1), and the hi(t)/h0(t) ratio (hazard ratio, HR) is obtained from the corresponding coefficient estimate: HR = exp(β̂1). The PH model suggests that the ratio between the hazard functions remains the same at all stages of the life cycle, i.e. does not depend on t. Diagnostic plots are constructed by plotting log-transformed estimated hazard function against the logarithm of time (log-cumulative hazard plot) [38]. In these plots, non-proportional hazards are indicated when hazard functions are non-parallel or intersect.
The accelerated failure time (AFT) model compares total survival curves, and not the probabilities of death at certain time points. The survival curves can be transformed into each other by substituting the variables: S1(λt) = S0(t). The biological meaning of this equation is that, even if a biological clock in running at different rates in two compared groups, the pattern of changes in the risk of death with age remains the same. The S1 and S0 curves will be stretched or compressed along the time axis relative to each other. The values of mean, median, and maximal lifespans will change proportionally.
Therefore, λ is a dimensionless factor that determines the strength of the effect that would be equal for any quantile. It could be expanded into components corresponding to individual factors that could be considered discrete states (control – experiment, high temperature – low temperature, different genotypes, etc.): λ = exp(β1x1· ... ⋅ βpxp), where xi is a variable coding for a particular discrete state of a factor, and βi is the effect of this factor on longevity [1, 39]. The effects of individual factors can be estimated by regression analysis from the data of a series of experiments [39]. In the absence of covariates, the only variable x1 is 0 for the control group and 1 for the experimental group, and β1 defines the aging deceleration factor λ according to the equation: λ = exp(β1). Sex, date of birth, parental characteristics, etc. can serve as covariates.
One of the main assumption of the AFT model is the multiplicativity of longevity-altering effects. For example, if some factor extends expected lifetime 1.2-fold (λ = 1.2), and the other factor extends it 1.5-fold (λ = 1.5), the combination of these two factors will extend lifetime 1.8-fold (1.2 × 1.5). The AFT model could be used not only for the lifespan estimation, but for predicting the moments of ontogenetic events (puberty, menopause, etc.).
The major advantage of this model, beside an intuitive way of result presentation, is the possibility of statistical analysis and confidence interval calculation for λ. On the other hand, it is based on an unobvious assumption that experimental interference produces quantitatively similar effects on subjects of different age. Moreover, it requires indication what parametric distribution determines the shape of the survival curve [39]. The Weibull distribution usually produces the best results, but, in general, the choice between the best and the second best (usually Gompertz’s) distributions does not noticeably affect the final results [39, 40].
Swindell [39] used both models to analyze raw data from studies on lifespan increase in mice caused by genetic manipulations to choose the model that fits best the experimental results. By applying the AFT model, he showed that the strongest effects on the mouse lifespan were caused by homozygous mutations Prop1 (λ = 1.48) and Pit1 (λ = 1.39). Less pronounced effects were observed for the homozygous mutation PappA and heterozygous mutations Clk1+/− and Irs2+/− in males (1.20 < λ < 1.40). Other genetic manipulations had similar but weaker effect (1.03 < λ < 1.20). The effect of the Irs2+/− mutation was significantly greater in males than in females, and the Clk1+/− mutation had dissimilar effects on each of two genetic backgrounds. In general, the AFT model well described the experimental results.
When the PH model was used, the hazard ratios noticeably varied between experiments and poorly correlated with the estimations of aging deceleration coefficient in the AFT model. In some cases, the HR values were absurdly high.
The AFT model appears to describe the effects of genetic manipulations on longevity most adequately in most cases. As mentioned before, it is often interpreted within the concept of a “biological clock” that could be slowed (lifespan extension) or accelerated (lifespan shortening). In contrast to the PH model, the AFT model usually does not require incorporation of age-dependent covariates to conform to the experimental data. In general, the AFT model produces results that are more resistant to random variations. In all the cases studied, the aging deceleration factors fell within a narrow interval (1.03 < λ < 1.48) and were precise, even when they depended on age (which formally conflicted with the model). The results predicted by the PH model, on the contrary, varied over a broad range (1.22 < HR < 515) and sometimes contradicted common sense. The main drawback of the AFT model is the assumption on the same shape of survival curves in the compared groups. Therefore, it cannot be used for comparing many species and populations whose survival curves have different shapes [33]. Moreover, studying effects of genetic manipulations demonstrated that in many cases these effects are age-dependent, which results in different shapes of survival curves in the control and experimental groups. Thus, partial inactivation of the receptor for insulin-like growth factor 1 in mouse brain (bIGF1RKO+/–) increased survival at the early stages of the mouse’s life cycle, but did not affect maximal lifespan and survival at the late stages [41].
Therefore, it seems reasonable to apply both models for analyzing results of each experiment and then to choose one that fits better. The assumption on the equal effects of the same manipulation at different ages is justified for lifespan-increasing mutations; however, its validity should be verified in each study.
General properties of Caenorhabditis elegans aging. Identification and quantification of aging markers are of extreme importance in studies of aging, because description of age-related changes is essential for understanding the aging process and of reasons that cause it.
The nematode C. elegans is often used for studies of aging because it has a lifespan of about two weeks and is easy to grow in the laboratory.
Aging is characterized by progressive deterioration of many tissues. The most obvious feature of aging is an increased risk of death of an individual organism. Aging in C. elegans is inseparably linked to the worm’s ability to move. Despite short lifespan, C. elegans displays pronounced traits of age-related degeneration, including sarcopenia and fertility loss after day 10 of life. Aging nematodes could be assigned to different age groups based on their motility and pharyngeal pumping that decrease due to age-related sarcopenia. Similar decline in physiological functions was observed in daf-2, age-1, daf-16, eat-2, and clk-1 mutants, despite altered lifespans [35, 42].
To reveal the relations between degenerative changes in C. elegans, Huang et al. developed a method for quantitative estimation of age-related changes and analyzed correlation between these changes in a longitudinal study [42]. Age-related decline in pharyngeal pumping and motility negatively correlated with longevity; a decrease in these parameters led to the decrease in the probability of survival [35, 42]. The method for easy classification and separation of aged C. elegans into three groups was developed based on the difference in the motility, which correlated well with the nematode’s lifespan: sluggish but rhythmically moving worms (type I), worms that moved irregularly (type II), and worms that did not move, but responded to touch (type III). These groups differed in their susceptibility to Nile Blue: type I worms were resistant to the dye; type II worms survived in 0.1% Nile Blue solution for 2 h, but 20-30% of worms died in 1% solution; all type III worms died in 1% Nile Blue [43]. Dambroise et al. [44] developed an assay for identification of physiologically old flies in a synchronized D. melanogaster population. Those individuals showed an age-dependent increase in intestinal permeability followed by a high risk of death. This physiological marker of aging in conserved in C. elegans, two Drosophila species, and zebrafish Danio rerio from the Cyprinidae family. The findings suggest that the intestinal barrier dysfunction may be an important event in the aging process conserved across a broad range of species, thus raising the possibility that it may also be the case in Homo sapiens [44].
GENETIC MANIPULATIONS AND LONGEVITY
Numerous longevity-increasing genetic manipulation have been discovered [39, 44-46], mostly in invertebrate model organisms [46], but only few have been studied in the context of mammalian aging. Aging-modulating genes have remained structurally and functionally conserved for more than a billion years, i.e. the genetic component that determines longevity has been well preserved in evolution [46].
Genomic screening of the model organisms C. elegans and Saccharomyces cerevisiae showed that lifespan can be increased by manipulating the activity of 0.1-3% of the total number of genes [45]. Smith et al. [46] were the first to perform quantitative analysis of the degree to which longevity genes are conserved between the two highly divergent eukaryotic species, the yeast S. cerevisiae and the nematode C. elegans. They found that when orthologs of worm aging genes were deleted in yeast, 15% of these deletions increased yeast lifespan. In contrast, only 3.4% of a random set of deletion mutants were long-lived.
The insulin/insulin-like growth factor-1 signaling pathway (IIS) was the first signaling pathway whose important role in the regulation of longevity in C. elegans was demonstrated [67]. Since then, numerous genes involved in aging regulation and, probably, mediating effects of external factors on the rate of aging and longevity have been identified (Table 1).
Table 1. Some genetic, chemical and
conditions of cultivation manipulations that alter lifespan in C.
elegans
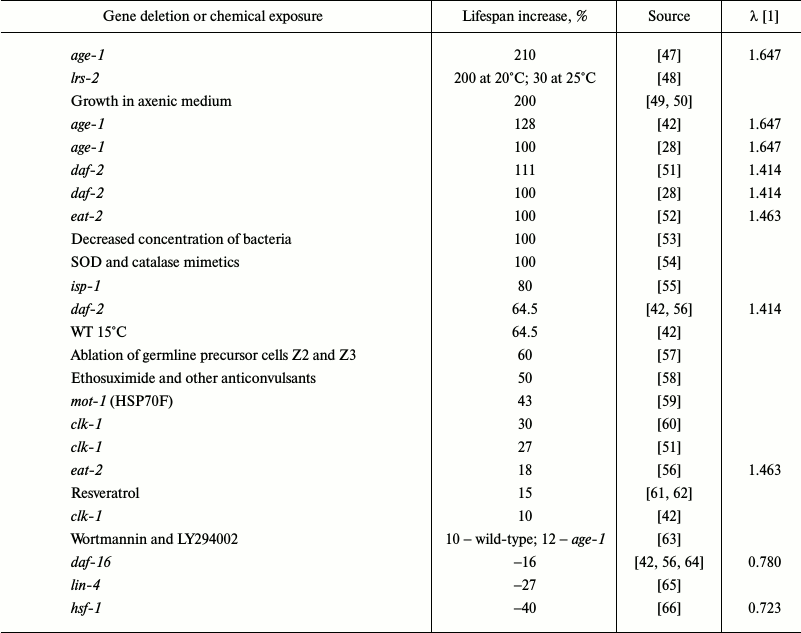
In C. elegans, mutations diminishing the activity of DAF-2, an insulin/IGF-1 receptor, increased lifespan more than two-fold [28]. AGE-1 is a downstream target of IIS and a homolog of PI3K. Mutations in the age-1 gene significantly lengthened lifespan [68]. Null mutations in the daf-16 gene that encodes three members of the Forkhead family of transcription factors suppress the effects of mutations in the IIS genes daf-2 or age-1 [69]. Proteins DAF-2, AGE-1, and DAF-16 are key components of IIS. Moderate inhibition of this pathway increases longevity and stress resistance in various species. Low IIS activity causes DAF-16 translocation into the nucleus, where it modulates the activity of genes involved in metabolism regulation, autophagy, and response to stress factors (heat shock proteins, superoxide dismutase (SOD), catalase) [48]. Taken together, these effects increase lifespan. Overexpression of DAF-16 in wild-type animals only slightly increases longevity [70], and the nuclear localization of DAF-16 is insufficient for lifespan increase. Canonical motifs for DAF-16 binding were found in the 5-kb regions located upstream of 78% of C. elegans genes, but only a few of these regions are active in early adulthood [71]. Obviously, DAF-16 is not the only factor that affects longevity. Lifespan increase in daf-7 mutants also depends on DAF-16 [72]. Since daf-7 codes for a protein of the TGF-β family, TGF-β could be an upstream regulator of IIS. The activity of DAF-16 is regulated by the ubiquitin–proteasome system. Disruptions in the ubiquitin ligase E3-encoding rle-1 gene increased lifespan [73], while inactivation of the math-33 gene coding for deubiquitinase suppressed increase in the lifespan in daf-2 mutants [74]. Mutations in hsf-1 (heat-shock transcription factor-1 homolog) [66], skn-1 (nuclear respiration factor 2 homolog) [75], and pqm-1 (C2H2-type zinc finger motif and leucine zipper domain protein) [76] genes also prevent lifespan increase in daf-2 mutants. It appears that HSF-1, SKN-1, and PQM-1 act cooperatively with DAF-16 and control overlapping sets of longevity-regulating genes. SKN-1 is activated by MPK-1, a homolog of ERK MAP kinase, and it regulates the activity of DAF. Restoration of daf-2 and age-1 expression to normal levels in the mutants abolishes the effects of the mutations in neurons, but not in intestinal cells [77].
TOR (target of rapamycin) is a serine/threonine kinase that regulates cell growth, proliferation, mobility, and survival, as well as protein synthesis, autophagy, and transcription [78]. TOR is activated when nutritive compounds and energy are available is sufficient amounts. It activates growth pathways and blocks the pathways that prevent expenditure of resources, such as reutilization via autophagy. Inhibition of TOR activity mimics nutrition and energy deficit and increases longevity in C. elegans via the DAF-16-dependent mechanism [79]. These effects are mediated by the PHA-4/FoxA transcription factors. PHA-4 regulates autophagy. A combination of two lifespan-prolonging genetic modifications – inactivation of the daf-2 gene and inactivation of the rsks-1 gene (coding for S6 kinase, a target of TOR) – additively increase the lifespan [80]. Therefore, longevity is regulated by both the IIS and TOR signaling pathways. Inhibition of TOR activity by caloric restriction increases lifespan via PHA-4 induction. During starvation, TOR inhibits IIS, which increases longevity. The effects of the TOR pathway on longevity might be either positive or negative depending on conditions.
Sirtuins (NAD-dependent deacetylases) directly participate in the oxidative exchange that involves NAD+. Sir2 is a positive regulator of longevity in yeast and C. elegans. Sir-2.1 overexpression in C. elegans increases lifespan via the DAF-16-dependent mechanism [81]: SIR-2.1 binds to and activates DAF-16 in response to stress. Mutations in the sir-2.1 gene suppress many lifespan-increasing effects. Apparently, sirtuins play a positive role in longevity regulation. Nevertheless, in many cases an increase in lifespan does not depend on sirtuins.
AMP-activated protein kinase (AMPK) is a conserved protein that acts as an energy sensor and helps cells to adapt to energy deficit. It stimulates catabolic processes and suppresses energy-demanding processes. Null mutations of the AMPK-encoding gene aak-2 decreased lifespan in C. elegans, while AMPK overexpression increased it [82].
Inhibition of the H3K4me3 complex (ASH-2, WDR-5, SET-2) and overexpression of the H3K4me3 demethylase RBR-2 increased lifespan in C. elegans. The effect depends on the production of mature eggs and could be inherited for up to four generations [83]. Inhibition of the H3K27 demethylase UTX-1 also increases lifespan [84].
MicroRNA (miRNA) lin-4 regulates longevity in C. elegans [65]. The effects of lin-4 and its target LIN-14 are mediated by IIS. Longevity is regulated by other miRNAs as well [36]. Thus, miR-71 and miR-228 are critical for lifespan increase in response to dietary restriction [85]. They negatively regulate PHA-4/FoxA and SKN-1/Nrf2, and their expression is controlled by PHA-4.
Hypoxia-inducible factor 1 (HIF-1) is the major regulator of the organism’s response to hypoxia, and its overexpression considerably increases longevity [86]. HIF-1 mediates the lifespan increase induced by paraquat and inhibition of respiration. Neuronal HIF-1 increases lifespan by regulating expression of flavin-containing monooxygenase-2 (FMO-2) in the intestine via serotonin signaling [87].
Huang et al. studied age-related decline in physiological processes and changes in the longevity in C. elegans mutants daf-2, age-1, daf-16, eat-2, and clk-1. They generated a system of four stages that describes the aging process and is useful for analysis of genetic and environmental effects on aging [42].
Similarly, Johnson et al. [56] compared the mortality profiles of over 100,000 wild-type C. elegans nematodes to the profiles of single-gene longevity mutants and revealed segmental (age-specific) effects of mutations in the age-1, clk-1, and spe-26 genes [56]. The age-1 mutation lowered mortality more than fivefold at the latest age. In contrast, the spe-26 mutant had a tenfold lower mortality until approximately 2 weeks of age but ultimately achieved higher mortality, whereas clk-1 mutants showed slightly higher mortality than the wild-type nematodes during the fertile period, i.e. early in life, but ultimately leveled off at lower mortality.
MATHEMATICAL ANALYSIS OF SURVIVAL CURVES
Nematode Caenorhabditis elegans. In the study by Stroustrup et al. [1], worms were subjected to the action of various factors (temperature, oxidative stress, lifespan-extending diet, genetic mutations) that either increased or decreased longevity. Statistical analysis of mortality in large populations showed that interventions as diverse as changes in diet, temperature, exposure to oxidative stress, and inactivation of genes, including hsf-1, hif-1, and the IIS components daf-2, age-1, and daf-16, all altered lifespan distributions by an apparent stretching or sinking of time (temporal scaling) [1]. The effects of temperature and peroxide on the lifespan of mutants in the IIS genes daf-2, daf-16, and age-1 have been studied in detail.
Each mutant population displayed a characteristic lifespan distribution that could be rescaled from the wild-type distributions observed at either 20 or 33°C. No significant temperature-dependent deviations from temporal scaling were identified within two thermal ranges: 19-30 and 30.5-33°C. Up to a certain limit, the effect of temperature on the lifespan was insignificant (e.g. the lifespan decreased 1.59-fold on transition from 20 to 27°C). Populations at higher temperatures exhibited more pronounced effect: 3.64-fold decrease at 29°C and 6.8-fold decrease at 30°C, i.e. upon transition into the next thermal range [1].
Stroustrup et al. evaluated the effect of the oxidant tert-butyl hydroperoxide (tBuOOH) and found that it quantitatively rescaled lifespan distributions in a dose-dependent manner up to 3 mM with significant deviations observed only at 6 mM [1]. Elimination of DAF-16 in the presence of tBuOOH reduced lifespan by a constant value (19.5 ± 8.8%) across all the concentrations tested. They concluded that DAF-16 acts antagonistically but in parallel to the mechanisms tough which tBuOOH and temperature shorten lifespan. DAF-16, tBuOOH, and temperature appear to affect aging tough their influence on risk determinants downstream of all tee [1]. The magnitude of temporal scaling produced both by daf-2(e1368) and by age-1(hx546) alleles varied across tBuOOH concentrations, which seems yet another aspect of a quantitative stress-dependent regulation of DAF-16 present in these strains but absent in wild type [1].
Inactivation of daf-2, daf-16, hif-1, or hsf-1 genes [66, 71], diet [88] and temperature [89] changes, and tBuOOH [90] cause pronounced metabolic, cellular, and behavioral consequences. Nevertheless, temporal scaling takes place irrespectively of molecular targets specific for each of these interventions and requires all risk determinants to be affected to the same extent. The only exceptions were mutations in two genes: eat-2 mutation that disturbed the feeding behavior of worms, and nuo-6 mutation that disrupted the activity of mitochondrial respiratory chain complex I (nuo-6 mutants consumed less oxygen and moved slower, but lived longer). These mutations altered the shape of the survival curve by making it less steep (i.e. increased the coefficient of variation, CV). But even in these mutants, other lifespan-modulating factors resulted only in temporal scaling of the new survival curve.
Stroustrup et al. interpreted these results as a proof for the existence of genetic programing of the survival curve shape. Each scaling regime appears to correspond to a distinct molecular mechanism and barrier process dominating the timescale of aging [1]. This is altogether unexpected, because it implies that the tested lifespan-altering manipulations change the probability of every possible cause of death in a coordinated manner and to the same extent [34]. Almost ideal time scaling under drastically different conditions puts certain limitations on the ways, how these conditions affect survival [34]. One possible formal explanation is that every cause of death in the worms has the same activation energy and responds identically to changes in food source, toxic exposures, and genetic mutations. Since this is highly improbable, we should consider another explanation, namely, that all worms have a single mechanistic cause of death. A more plausible interpretation is that there is some intermediate state, on which all the tested interventions converge [34]. This state had been postulated by Gavrilov [31], who speculated about a transition to an extremely vulnerable state, i.e. from “survivalist” to “non-survivalist”.
It should be noted that the observations of Stroustrup et al. do not necessarily mean the discovery of an aging program universal for all living organisms. The AFT model is widely accepted; it can be successfully applied not only to worms, but also to mice and flies, as well as to inanimate objects, such as pieces of machinery and even nuts and bolts. To suggest the existence of an aging program for such a broad range of subjects would be an exaggeration. Most probably, what is involved here is the resistance of a certain subject toward various factors. This is of great importance for the biology of aging, since it reveals molecular responses of an organism to an intervention, although the mechanisms of transition from “survivalist” to “non-survivalist” are numerous and programmed.
In the work of Stroustrup et al. [1], the major flaw of the AFT model has been turned into an advantage: the temporal scaling of survival curves described by the AFT model was considered as the zero hypothesis, the deviation from which could indicate qualitative changes in the aging dynamics.
The adaptation of the Kolmogorov–Smirnov test by Stroustrup et al. revealed deviations from temporal scaling when using censored data, when many individuals left the experiment before their death (including by age-unrelated death). It should be noted that this adaptation does not require prior knowledge or prediction of the survival curve shape usually needed for quantitative assessment of the longevity-modulating factors in the AFT model. They found that survival curves retain their shape even when IIS, which is central to many aspects of aging across species, was inactivated, and in response to conditions and mutations known to act independently of IIS [34].
The most logical explanation for these observations is the existence of multiple causes of death. In other words, the risk of death is governed not by any single pathway, but by an organism’s property that arises from interactions between the various molecular processes that influence aging. This property, perhaps best called “resilience”, would be an intrinsic biological property of aging C. elegans, just as temperature and pressure are intrinsic thermodynamic properties of gases that emerge from the interactions of the constituent molecules. Similarly, alterations in the molecular processes that contribute to resilience could change the rate of aging without changing the shape of the survival curve [34].
Alternatively, a single physical property (e.g. intracellular redox levels [91] or global protein solubility levels and turnover rates [92]), which is acted on by many molecular processes and affects the risk of death from diverse causes, could underlie resilience. Drastic decrease in lifespan in Drosophila at 30°C [93] coincides with deviation from temporal scaling of lifespan distribution in C. elegans, which suggests the importance of this temperature in the aging of cold-blooded animals.
The influence of interventions from one to all risk determinants produces a system-wide property r(t) [1]. The temporal scaling of lifespan distributions constrains the dynamics of the state variable r(t): the single stochastic process determining C. elegans lifespan must be invariant to timescale transformations and follow average dynamics governed by a single effective rate constant: dr/dt = −krF(r), where F(r) is an unknown function of r that does not depend on kr. In this formulation, temporal scaling arises when interventions change kr into kr/λ [1]. F(r) determines the curve shape, which is stretched or compressed by λ. It can be different for different organisms.
Fruit fly Drosophila melanogaster. In the earlier work [94], we studied survival curves of Drosophila flies grown for several generations on normal medium (Mn), starch medium (Ms), and flies that had access to starch and salt media (Mss) (lines 1, 2, and 3, respectively, in Table 2a). The average lifespans of Ms and Mss flies were shorter than of Mn flies: 69.1 and 75.0 days vs. 88.1 days, respectively. Environmental factors (diet) and evolutionary changes (adaptation to different medium) altered average lifespan over a broad range [94].
Table 2a. Comparison of survival in flies
grown on normal (N) and starch (S) media. Mn, Ms, and Mss lines are
designated with 1, 2, and 3, respectively. The time scaling factors
(λ) are shown for the compared line relatively to the line of
comparison. Deviations from temporal scaling are in italics (p
< 0.006). Because of the nature of the criterion, we present
intervals instead of exact probability values. Lines, where comparison
methods used gave different results, are shaded
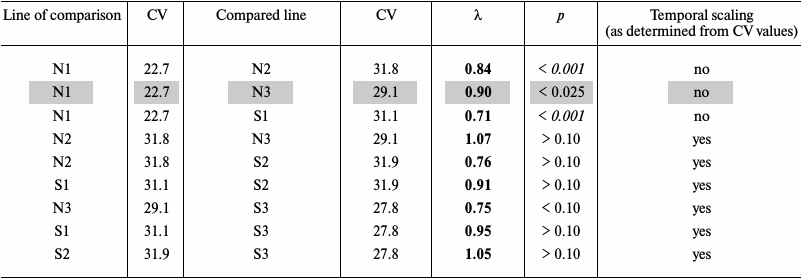
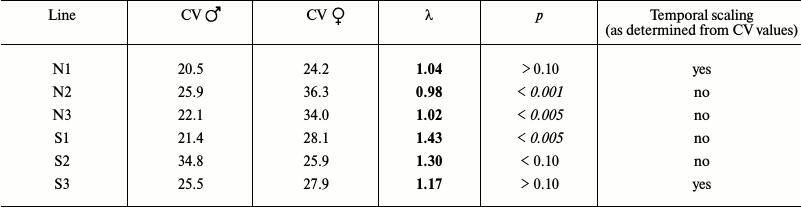
Table 2b. Comparison of male and female
flies
If the CV values differ by less than 10%, the shapes of the survival curves are similar, and we can speak about the presence of temporal scaling. For example, Ms flies grown on the normal and starch media displayed similar CV values (31.8 and 31.9), although their average lifespans differed (69.1 and 58.2 days, respectively). Therefore, temporal scaling took place in this case [94].
On the other hand, the CV values for the Mn flies grown on the normal and starch media differed considerably (22.7 and 31.1, respectively), as well as the shapes of their survival curves (more convex for the former), i.e. scaling is not observed. Combined data for both genders showed that in 5 of 6 cases, the CV values were very similar (from 27.8 to 31.9), and only in control (Mn flies grown on normal medium) the CV value was significantly lower (22.7) [94].
Our goal was to compare S1 to N1, S2 to N2, and S3 to N3 lines (flies of the same line grown on different media) to estimate phenotypical plasticity, and N2 to N1, N3 to N1, N3 to N2, S2 to S1, S3 to S1, and S3 to S2 lines (flies of different lines grown on the same medium) to estimate evolutionary changes. We used the method suggested by Stroustrup et al. [1] with slight modification, since our data were not censured, i.e. we knew exact lifespans of all flies. The data were expressed as base 10 logarithms and then reduced to a common time scale by dividing by the average lifespan in a group. After conversion, all the data had the same mean value equaling 1 in all groups. Distributions of the deviations from the mean in different groups were compared pairwise using the Kolmogorov–Smirnov test with Bonferroni adjustment (required for multiple pairwise comparisons to decrease the probability of false positives [95]). Significant differences in the distributions indicated deviations from temporal scaling. Statistical analysis was performed with the Statistica program.
Four of six survival curves had similar (flattened) shape that differed considerably from the convex shape of the survival curve for Mn flies grown on N medium, which correlated well with the results obtained in [94]. However, our conclusions on the existence of temporal scaling derived from the CV values differed from the conclusions made using the method of Stroustrup et al.; moreover, both false positives and false negatives were obtained. Note that unlike the method of Stroustrup et al., the “Markov method” does not provide the significance levels: the statement “if CV values differ by less than 10%, the shapes of the survival curves are similar, and we can speak about the presence of the temporal scaling” implies the existence of a critical value of differences that does not depend on the sample size. Therefore, the “Markov method” is simple to use and suggests the existence of temporal scaling, but the conclusions should be verified by the method of Stroustrup et al. Moreover, the Markov method definitely does not allow us to identify the scale at CV values ratio more than 1.1 (or less than 0.9).
When the data for female and male flies were evaluated separately, the picture was more complex, but still rather similar overall: in some cases, the CV values (and the shapes of survival curves) were similar, which suggested the presence of temporal scaling, while in other cases, there was no scaling (Table 2b).
The ranges for the CV values and the shapes of the survival curves are similar in D. melanogaster and C. elegans. This is not the case in other species (see Jones at al. [2] and [33] for more details).
Mice Mus musculus.As the initial step in fitting the AFT model, Swindell [39] tested which parametric distribution (exponential, Weibull, Gompertz, log-normal, etc.) should be specified for the survival time Ti of genetically modified mice to minimize AIC (Akaike’s Information Criterion) [96]. Weibull distribution was the most appropriate in almost all cases, although the exact choice of distribution proved to be of limited consequence: when deceleration factor estimates were compared between the best and the next-best distributions (AIC criterion), estimates differed by only 3.9% on average (0.3-11.4%). Moreover, the statistical significance of deceleration factor estimates differed for only two of 22 comparisons (mutants TRX-Tg and p66).
In general, the AFT model adequately described effects of interventions on survival time. For 18 of 22 comparisons, there was no significant evidence that genetic manipulations altered the Weibull shape parameter of survival time distributions (except in mutants bIrs2−/−, bIrs2+/−, fIr−/−, and Klotho). There were six comparisons for which the AFT model was questionable (Irs2+/−(M), bIrs2−/−, bIrs2+/−, Igf1r+/−(F), Clk+/−(S2), TRX-TG). In each case, a similar trend was present, in which the treatment effect was strong at early age, but weakened at more advanced age. This could be a direct consequence of a legitimate dependence of the effect strength on age, but could also result from the absence of important (unmeasured) covariate variables. Nevertheless, even in these six cases, the deceleration factor estimates were still informative and represented an average between the strong and weak effects early and late in life.
Omission of outlying observations (most often, especially long-lived individuals from the control cohort) only slightly affected the results, except in the Prop1(df/df) and Clk1+/−(S2) mutants, for which it increased λ from 1.48 to 1.54 and from 1.32 to 1.41, respectively.
When the PH model was used, the hazard ratios noticeably varied between comparisons and poorly correlated with the deceleration factor estimates calculated using the AFT model (r = 0.22, rs = 0.71). In some cases, exceedingly large hazard ratios were obtained. For example, the hazard ratio estimated for the Irs2+/−(M) comparison suggested that age-specific mortality rates were 515 times greater in the control cohort compared to the experimental cohort. In comparison to the AFT model approach, the PH model hazard ratios are less stable and more sensitive to deviations from model assumptions. In general, the proportional hazards assumption was questionable for half of the comparisons (p66−/−, αMUPA, bIrs2+/−, MCAT, Clk1+/−(S1), Klotho, bIrs2−/−, TRX-Tg, Hcrt-UCP2, Surf1−/−, Igf1r+/−(F), Ghr−/−, Gpx4+/−), as indicated by crossing of log-transformed hazard functions of control and experimental treatments. The proportional hazards assumption was most clearly violated for the bIrs2+/− and bIrs2−/− comparisons (p < 0.01); its was also doubtful for the Surf1−/− comparison.
Apparently, the AFT model mostly adequately describes the effects of genetic manipulations on longevity and produces results that are less sensitive to random deviations than the results of the PH approach.
An interesting aspect of this side-by-side comparison is the decline in survivorship effects among mutations that inhibit increasingly downstream elements of the growth hormone/insulin-like growth factor I (GH/IGF-I) signaling pathway: Prop1(df/df), Pit1(dw/dw), Ghrhr(lit/lit), Ghr−/−, PappA−/−, Igf1r+/−(F), Irs2+/−(M), Irs2+/−(F), bIrs2+/−, bIrs2−/−. The Prop1(df/df) and Pit1(dw/dw) mutations have the strongest overall effects on survivorship, which might be related to prolactin or thyroid stimulating hormone deficiencies in these mutants.
COEFFICIENT OF LIFESPAN VARIATION
In their commentary to the paper by Stroustrup et al., Markov et al. described other examples of temporal scaling that they identified using another criterion, such as stability of the coefficient of lifespan variation upon changes in the lifespan [94]. This approach is based on the fact that CV indeed does not change with temporal scaling.
However, this does not mean that stable CV always indicates temporal scaling. It is possible to imagine a situation when two theoretical distributions with different mean values but same CVs will have differences in their shapes described by the highest moments (e.g. asymmetry). This situation indicates the absence of programming or, most probably, a switch between several programmed regimes – for example, when subjects die mostly at young age, but they are outlived by a few long-lived individuals (super-long lives). Or when almost no subjects die at a young age, but aged individuals die within a short period and have no tendency for long life.
In these cases, the method of Stroustrup et al., which directly compares survival curves, will reveal deviations from temporal scaling. This is especially important, because in many animals the lifespan distribution curve displays right asymmetry [31].
It would be interesting to explore the validity of CV application as an indicator of temporal scaling by the methods of power analysis to reveal if it can identify deviations in the curve shape.
Gavrilova et al. [97] used CV to answer the question whether longevity is programmed. They analyzed the data of a survey of adult population of the United States (MIDUS) and published data for 14 other countries to test the validity of the argument from the opponents of the “programmed longevity” that variations in individual lifespans and the timing of aging-related events considerably exceed variations in timing of the events programmed by ontogenesis [98]. They found that in humans, relative variabilities (coefficients of variation) for parameters of development and aging are similar. For example, relative variability in the age at menarche (an ontogenesis-controlled event) was almost equal to relative variability of the age at menopause (an aging-related event). The CV values were 8-13% for age at menarche, 7-11% for age at menopause, and 16-21% for age at death. Therefore, the relative variability for the age at death is only twice higher than for the age at menarche, while the relative variability for the age at menopause is almost the same as for the age at menarche [97].
The idea that aging is related to changes in the physiological state of an organism has been suggested based on such concepts as organization, vitality, organism reserves, and resistance [10, 99]. Any aspects of C. elegans physiology that change with time but do not alter longevity, i.e. affect the “quality”, but not the “quantity” of life, do not have to change in accordance with r(t) [1].
We do not know which physiological factors affect r(t) or what are the dynamics of their changes with age. Nevertheless, it could be expected that a broad range of longevity determinants alter kr only. Future studies should be aimed at understanding the nature of r [1].
Stroustrup et al. found several factors that change the survival curve shape in C. elegans (e.g. eat-2 mutation that disturbs the feeding behavior of worms, and nuo-6 mutation that disrupts mitochondrial functions), which might show the way for deciphering these mechanisms. However, the nature of the organism’s vulnerability remains unknown. Pincus suggested that the frailty index (FI) [100], which calculates the fraction of measured clinical markers considered to be in a deficient state, is a close theoretical match for “resilience” [34].
Finally, Stroustrup et al. analyzed only chronological increase in lifespan, but not necessarily in healthspan [34]. Thus, to evaluate the heterogeneity in the health status and aging rate, Mitnitski et al. [100] suggested that the health status could be quantified from the number of health deficits that individuals accumulate. Specifically, the frailty index (FI) is the ratio of the deficits present in a person to the total number of potential deficits evaluated (e.g. in a database or in experiment). Changes in FI characterize the rate of individual aging: FI increases with age according to the Gompertz law. It is strongly associated with adverse outcomes, including mortality, shows higher values in females, and has a universal limit of ~0.7.
Mitnitski et al. showed that the average number of deficits in humans is a product of the average intensity of ecological stresses and average rehabilitation time. Age-associated increase in the rehabilitation time results in the accumulation of deficits (i.e. gradual transition from “survivalist” to “non-survivalist” according to Gavrilov [31]). This explains not only why the number of deficits could be used for estimating differences in the individual aging rates, but also suggests that various measures that speed rehabilitation (prophylactic or therapeutic interventions) will decrease the number of deficits, hence increase the lifespan [100].
Different scientists answer differently the question if aging is programmed. Some believe that a specific genetic program for aging does not exist [8, 98, 101]; others accept the possibility of the existence of both programmed and random components of the aging process [5, 21, 24, 102-104].
Many manipulations (either genetic or ecological) increase longevity in C. elegans. Many lifespan-increasing modifications could be viewed as ways to “cheat” signaling pathways by imitating the deficit of resources or the presence of damaging agents. This can result in “investment” of resources into somatic maintenance, which will decrease the damage of cellular components to the minimum. Henderson et al. suggested that lifespan increase is mediated by changes in the functioning of TOR and IIS pathways [60]. Similarly, studies of several gerontogenes have emphasized the role of energy metabolism control. For example, overexpression of the AMP-activated protein kinase increases longevity [105]. Interaction of aak-2 with other pathways controls aging in worms. Lifespan extension caused by IIS mutations is highly dependent on aak-2, as is the lifespan extension caused by overexpression of deacetylase sir-2.1. It should be noted that in nature reproduction is more important that longevity, and resources should not be wasted. The inability of age-1 mutants to survive in competition with wild-type worms when environmental conditions change confirms this idea [106]. Therefore, all interventions that increase lifespan in C. elegans could be divided into tee major categories: (i) non-stressogenic changes that result in the activation of stress response pathways (sensory and signaling pathways) under conditions that do not require it; (ii) changes that are not harmful by themselves, but decrease the availability of resources to the extent that it activates repair pathways (food restriction); (iii) nonlethal stress measures that mobilize an organism to respond to stress and to overcome the deteriorating effect of stress factor (hormesis). Stroustrup et al. showed that survival could be described by the AFT model after virtually any intervention used (temperature, gene inactivation, treatment with peroxide). This means that these interventions only stretch or compress the survival curve along the x-axis (time axis) but do not change its shape [1]. In the biological sense, the longevity-altering mechanisms for these interventions are the same. They, as well as Markov et al. [94], believe that these results could be explained by the fact that experiments were performed in such primitive animals, as worms, in which many age-regulating pathways converge and overlap. However, the AFT model has been successfully used in Drosophila [94] and mice [39], species that considerably differ from nematodes in their positions on the evolutionary tree.
In terms of the AFT model, equal CV values for the distributions of lifespans in the control and experimental groups mean that all lifespan-altering factors changed to the same extent (by the same percent), which is impossible if the process of lifespan regulation is random. According to Stroustrup et al., stable CV values indicate that aging pathways are programmed and the probability of death increases with age. We believe that what is involved here is the programing of cell signals that regulate longevity in living organisms. The fact that one of the authors of this article demonstrated the existence of temporal scaling upon diet change in some Drosophila strains, but not in others, serves as an indirect proof of our point of view. It is difficult to imagine that one strain of Drosophila would have an aging program, and the other would not.
Weismann’s hypothesis on aging as an adaptive mechanism of programmed death could be united with an alternative point of view that aging results from accumulation of lesions and errors. Such accumulation might be monitored by specific systems that would send activation signals to initiate the programs of chronic or acute phenoptosis. If we consider aging a stochastic process, it makes it difficult to believe that gene mutations, that are in fact induced genome lesions, can improve organism functioning or increase lifetime. Nevertheless, over 500 mutations have found that extend longevity in various animals. The effect is stronger in short-lived species with pronounced aging (group III) [33].
Table 1 shows over 30 mutations, most of which increase average lifespan in C. elegans. The most extensively characterized pathway that regulates longevity in C. elegans is IIS [23]; mutations in the components of this pathway alter lifespan to the greatest extent (Table 1). Other pathways can influence lifespan in an IIS-mediated manner or by directly modulating (either activating or suppressing) IIS. Note that IIS is strongly inhibited in the “aging-resistant” naked mole rat Heterocephalus glaber [107].
Based on these data, we assume that IIS is responsible not for the mechanism of aging, but for the rate of aging, and therefore acts as a natural regulator of mortality level. IIS inactivation increases life span 2-3-fold. Hence, IIS activation decreases lifespan. DAF-16 partially counteracts this effect – DAF-16 inactivation decreases longevity by 20-30% only (Table 1).
It should be noted that if in nematodes (as well as in other animals) gene knockouts change temporal scaling 2-3-fold, then peroxide treatment – up to 17-fold, and temperature change – up to 7-fold. Further increase in the concentration will decrease lifespan, but it will also disturb temporal scaling. Stroustrup et al. identified tee temperature intervals with different temporal scaling that supposedly characterized different mortality-regulating mechanisms. The effects of IIS gene knockouts were also different in the tee temperature intervals, except for daf-16.
Swindell showed that effects of experimental interventions on survival were similar at the early, middle, and late stages of the lives of mice [39]. In this case, scaling coefficients reflected the effects at all ages (including late age) and could provide information on the maximal lifespan. Nevertheless, Swindell identified six genetic manipulations whose effects were more pronounces at the beginning than at the end of life (Irs2+/−(M), bIrs2−/−, bIrs2+/−, Igf1r+/−(F), Clk1+/−(S1), TRX-TG). For these comparisons, scaling coefficients of the AFT model provided “averaged” estimation of the effect strength over the whole lifetime, but overestimated the effect at later age.
Stroustrup et al. verified the test power using Weibull distribution (i.e. they analyzed how well the test identified deviations from temporal scaling). They found that the sample size required for revealing such deviations should be 500-1500 animals (at 10% censured data). If smaller samples are used, the deviations might remain unnoticed. Note the ease of calculations and broad applicability – curves with very different scaling of the time axis could be compared, as well as curves with one and not two parameters (as by Gompertz).
As far as we can judge, verification of the AFT model (modification of the Kolmogorov–Smirnov test) proved that this model works in many cases. At the same time, Stroustrup et al. specify that the temporal scaling model cannot be applied in all cases, since some species have apparently different survival curves.
In general, the AFT model provides results that are more resistant to random variations than the PH model. In all the cases studied, aging deceleration factors predicted by the AFT model fell within a narrow interval (1 < λ < 2) and were relatively precise, even when they depended on age, which formally contradicts the model. We suggest that the use of temporal scaling allows, most importantly, to distinguish quantitative differences in aging dynamics from qualitative ones. Thus, when testing mechanical parts, the impact of load on the part will change with changes in the load, but the temporal scaling of the “aging” (wear) will be retained. The cessation of the temporal scaling means that the part broke, i.e. quantitative changes transformed into qualitative ones. Apparently, mechanical parts do not have an aging program; the temporal scaling reflects intrinsic features of their inner structure and the properties of materials these parts are made of. The possibility to monitor the moment of switch from the longevity-governing mechanism to some other pathways might be useful in testing various geroprotective drugs.
Acknowledgements
We thank E. Yu. Yakovleva, I. D. Kan, and L. S. Yaguzhinsky for helpful remarks and advice when writing this article.
This work was supported by the Russian Science Foundation (project No. 14-50-00029).
REFERENCES
1.Stroustrup, N., Anthony, W. E., Nash, Z. M.,
Gowda, V., Gomez, A., Lopez-Moyado, I. F., Apfeld, J., and Fontana, W.
(2016) The temporal scaling of Caenorhabditis elegans ageing,
Nature, 530, 103-107.
2.Jones, O. R., Scheuerlein, A., Salguero-Gomez, R.,
Camarda, C. G., Schaible, R., Casper, B. B., Dahlgren, J. P., Elen, J.,
Garcia, M. B., Menges, E. S., Quintana-Ascencio, P. F., Caswell, H.,
Baudisch, A., and Vaupel, J. W. (2014) Diversity of ageing across the
tree of life, Nature, 505, 169-173.
3.Baudisch, A. (2008) Inevitable Aging?
Contributions to Evolutionary-Demographic Theory,
Springer-Verlag, Berlin-Heidelberg.
4.Skulachev, M. V., and Skulachev, V. P. (2014) New
data on programmed aging – slow phenoptosis, Biochemistry
(Moscow), 79, 977-993.
5.Skulachev, M. V., Severin, F. F., and Skulachev, V.
P. (2015) Aging as an evolvability-increasing program, which can be
switched off by organism to mobilize additional resources for survival,
Curr. Aging Sci., 8, 95-109.
6.Comfort, A. (1979) The Biology of
Senescence, Churchill Livingstone, Edinbourgh-London.
7.Medvedev, Z. A. (1990) An attempt at a rational
classification of theories of ageing, Biol. Rev. Camb. Philos.
Soc., 65, 375-398.
8.Kirkwood, T. B. L. (2010) Systems biology of ageing
and longevity, Phil. Trans. R. Soc. B., 366, 64-70.
9.Fisher, R. A. (1930) The Genetic Theory of
Natural Selection, Clarendon Press, Oxford.
10.Medawar, P. B. (1952) An Unsolved Problem of
Biology, H. K. Lewis, London.
11.Hamilton, W. D. (1966) The moulding of senescence
by natural selection, J. Theor. Biol., 12, 12-45.
12.Severtsov, A. S. (2005) Evolutional Theory
[in Russian], Vlados, Moscow.
13.Putiatina, T. S. (2011) Effect of recreational
pressure on ant communities of open biocenoses in Moscow, Moscow
Univ. Biol. Sci. Bull., 66, 42-45.
14.Zorina, Z. A., Poletaeva, I. I., and Reznikova,
Zh. I. (1999) Principles of Ethology and Genetics of Behavior
[in Russian], Moscow State University, Moscow.
15.Nusbaum, N. J. (1996) What good is it to get
old? Med. Hypotheses, 47, 77-79.
16.Williams, G. C. (1957) Pleiotropy, natural
selection and the evolution of senescence, Evolution, 11,
398-411.
17.Vijg, J., and Suh, Y. (2005) Genetics of
longevity and aging, Annu. Rev. Med., 56, 193-212.
18.Campisi, J. (2005) Aging, tumor suppression and
cancer: high wire-act! Mech. Ageing Dev., 126, 51-58.
19.Weinert, B. T., and Timiras, P. S. (2003) Invited
review: theories of aging, J. Appl. Physiol., 95,
1706-1716.
20.Skulachev, V. P. (1997) Aging is a specific
biological function rather than the result of a disorder in complex
living systems: biochemical evidence in support of Weismann’s
hypothesis, Biochemistry (Moscow), 62, 1191-1195.
21.Skulachev, V. P. (1999) Phenoptosis: programmed
death of an organism? Biochemistry (Moscow), 64,
1418-1426.
22.Weismann, A. (1889) Essays upon Heredity and
Kindred Biological Problems, Clarendon Press, Oxford.
23.Guarente, L., and Kenyon, C. (2000) Genetic
pathways that regulate ageing in model organisms, Nature,
408, 255-262.
24.Longo, V. D., Mitteldorf, J., and Skulachev, V.
P. (2005) Programmed and altruistic ageing, Nature Rev. Genet.,
6, 866-872.
25.Ashapkin, V. V., Kutueva, L. I., and Vanyushin,
B. F. (2015) Aging epigenetics: accumulation of errors or realization
of a specific program? Biochemistry (Moscow), 80,
1406-1417.
26.Boyd-Kirkup, J. D., Green, C. D., Wu, G., Wang,
D., and Han, J. D. (2013) Epigenomics and the regulation of aging,
Epigenomics, 5, 205-227.
27.Zwaan, B., Bijlsma, R., and Hoekstra, R. E.
(1995) Direct selection on life-span in Drosophila melanogaster,
Evolution, 49, 649-659.
28.Kenyon, C., Chang, J., Gensch, E., Rudner, A.,
and Tabtiang, R. A. (1993) C. elegans mutant that lives twice as
long as wild type, Nature, 366, 461-464.
29.Markov, A. V. (2012) Can kin selection facilitate
the evolution of the genetic program of senescence? Biochemistry
(Moscow), 77, 733-337.
30.Bahar, R., Hartmann, C. H., Rodriguez, K. A.,
Denny, A. D., Busuttil, R. A., Dolle, M. E., Calder, R. B., Chisholm,
G. B., Pollock, B. H., Klein, C. A., and Vijg, J. (2006)
Increased cell-to-cell variation in gene expression in ageing mouse
heart, Nature, 441, 1011-1014.
31.Gavrilov, L. A., and Gavrilova, N. S. (1991)
The Biology of Life Span: A Quantitative Approach, Harwood
Academic Publisher, N. Y.
32.Khalyavkin, A. V (2001) Influence of
environment on the mortality pattern of potentially non-senescent
organisms. General approach and comparison with real populations,
Adv. Gerontol., 7, 46-49.
33.Shilovsky, G. A., Putyatina, T. S., Markov, A.
V., and Skulachev, V. P. (2015) Contribution of quantitative methods of
estimating mortality dynamics to explaining mechanisms of aging,
Biochemistry (Moscow), 80, 1547-1559.
34.Pincus, Z. (2016) Ageing: a stretch in time,
Nature, 530, 37-38.
35.Herndon, L. A., Schmeissner, P. J., Dudaronek, J.
M., Brown, P. A., Listner, K. M., Sakano, Y., Paupard, M. C., Hall, D.
H., and Driscoll, M. (2002) Stochastic and genetic factors influence
tissue-specific decline in ageing C. elegans, Nature,
419, 808-814.
36.Pincus, Z., Smith-Vikos, T., and Slack, F. J.
(2011) MicroRNA predictors of longevity in Caenorhabditis
elegans, PLoS Genet., 7, e1002306.
37.Cox, D. R. (1972) Regression models and
life-tables, J. Roy. Statist. Soc. Ser., 34, 187-202.
38.Collett, D. (2003) Modelling Survival Data in
Medical Research, Vol. 2, CRC Press, Boca Raton.
39.Swindell, W. R. (2009) Accelerated failure time
models provide a useful statistical framework for aging research,
Exp. Gerontol., 44, 190-200.
40.Swindell, W. R. (2016) Meta-analysis of 29
experiments evaluating the effects of rapamycin on life span in the
laboratory mouse, J. Gerontol. A Biol. Sci. Med. Sci., doi:
10.1093/gerona/glw153 (2016).
41.Kappeler, L., De Magalhaes Filho, C., Dupont, J.,
Leneuve, P., Cervera, P., Perin, L., Loudes, C., Blaise, A., Klein, R.,
Epelbaum, J., Le Bouc, Y., and Holzenberger, M. (2008) Brain IGF-1
receptors control mammalian growth and lifespan tough a neuroendocrine
mechanism, PLoS Biol., 6, e254.
42.Huang, C., Xiong, C., and Kornfeld, K. (2004)
Measurements of age-related changes of physiological processes that
predict lifespan of Caenorhabditis elegans, Proc. Natl. Acad.
Sci. USA, 101, 8084-8089.
43.Hosono, R., Sato, Y., Aizawa, S. I., and Mitsui,
Y. (1980) Age-dependent changes in mobility and separation of the
nematode Caenorhabditis elegans, Exp. Gerontol.,
15, 285-289.
44.Dambroise, E., Monnier, L., Ruisheng, L.,
Aguilaniu, H., Joly, J. S., Tricoire, H., and Rera, M. (2016) Two
phases of aging separated by the Smurf transition as a public path to
death, Sci. Rep., 6, 23523.
45.Kennedy, B. K. (2008) The genetics of ageing:
insight from genome-wide approaches in invertebrate model organisms,
J. Intern. Med., 263, 142-152.
46.Smith, E. D., Tsuchiya, M., Fox, L. A.,
Dang, N., Hu, D., Kerr, E. O., Johnston, E. D., Tchao, B. N.,
Pak, D. N., Welton, K. L., Promislow, D. E., Thomas, J. H.,
Kaeberlein, M., and Kennedy, B. K. (2008) Quantitative evidence for
conserved longevity pathways between divergent eukaryotic species,
Genome Res., 18, 564-570.
47.Murakami, H., Bessinger, K., Hellmann, J., and
Murakami, S. (2005) Aging-dependent and -independent modulation of
associative learning behavior by insulin/insulin-like growth factor-1
signal in Caenorhabditis elegans, J. Neurosci.,
25, 10894-10904.
48.Lee, S. S., Lee, R. Y., Fraser, A. G., Kamath, R.
S., Ainger, J., and Ruvkun, G. (2003) A systematic RNAi screen
identifies a critical role for mitochondria in C. elegans
longevity, Nat. Genet., 33, 40-48.
49.Houthoofd, K., Braeckman, B. P., Johnson, T. E.,
and Vanfleteren, J. R. (2003) Life extension via dietary restriction is
independent of the Ins/IGF-1 signaling pathway in Caenorhabditis
elegans, Exp. Gerontol., 38, 947-954.
50.De Cuyper, C., and Vanfleteren, J. R. (1982)
Oxygen consumption during development and aging of the nematode
Caenorhabditis elegans, Comp. Biochem. Physiol.,
73A, 283-289.
51.Chen, J., Senturk, D., Wang, J. L., Muller, H.
G., Carey, J. R., Caswell, H., and Caswell-Chen, E. P. (2007) A
demographic analysis of the fitness cost of extended longevity in
Caenorhabditis elegans, J. Gerontol. A. Biol. Sci. Med.
Sci., 62, 126-135.
52.Lakowski, B., and Hekimi, S. (1998) The genetics
of caloric restriction in Caenorhabditis elegans, Proc. Natl.
Acad. Sci. USA, 95, 13091-13096.
53.Klass, M. R. (1977) Aging in the nematode
Caenorhabditis elegans: major biological and environmental
factors influencing life span, Mech. Ageing Dev., 6,
413-429.
54.Melov, S., Ravenscroft, J., Malik, S., Gill, M.
S., Walker, D. W., Clayton, P. E., Wallace, D. C., Malfroy, B.,
Doctrow, S. R., and Lithgow, G. J. (2000) Extension of life-span with
superoxide dismutase/catalase mimetics, Science, 289,
1567-1569.
55.Feng, J., Bussiere, F., and Hekimi, S. (2001)
Mitochondrial electron transport is a key determinant of life span in
Caenorhabditis elegans, Dev. Cell, 1, 633-644.
56.Johnson, T. E., Wu, D., Tedesco, P., Dames, S.,
and Vaupel, J. W. (2001) Age-specific demographic profiles of longevity
mutants in Caenorhabditis elegans show segmental effects, J.
Gerontol. Biol. Sci., 56A, 331-339.
57.Hsin, H., and Kenyon, C. (1999) Signals from the
reproductive system regulate the lifespan of C. elegans,
Nature, 399, 362-366.
58.Evason, K., Huang, C., Yamben, I., Covey, D. F.,
and Kornfeld, K. (2005) Anticonvulsant medications extend worm
life-span, Science, 307, 258-262.
59.Yokoyama, K., Fukumoto, K., Murakami, T., Harada,
S., Hosono, R., Wadhwa, R., Mitsui, Y., and Ohkuma, S. (2002) Extended
longevity of Caenorhabditis elegans by knocking in extra copies
of hsp70F, a homolog of mot-2 (mortalin)/mthsp70/Grp75, FEBS
Lett., 516, 53-57.
60.Henderson, S. T., Bonafe, M., and Johnson, T. E.
(2006) Daf-16 protects the nematode Caenorhabditis elegans
during food deprivation, J. Gerontol. A Biol. Sci. Med. Sci.,
61, 444-460.
61.Viswanathan, M., Kim, S. K., Berdichevsky, A.,
and Guarente, L. (2005) A role for SIR-2.1 regulation of ER stress
response genes in determining C. elegans life span, Dev.
Cell, 9, 605-615.
62.Wood, J. G., Rogina, B., Lavu, S., Howitz, K.,
Helfand, S. L., Tatar, M., and Sinclair, D. (2004) Sirtuin activators
mimic caloric restriction and delay ageing in metazoans, Nature,
430, 686-698.
63.Babar, P., Adamson, C., Walker, G. A., Walker, D.
W., and Lithgow, G. J. (1999) P13-kinase inhibition induces dauer
formation, thermotolerance and longevity in C. elegans,
Neurobiol. Aging, 20, 513-519.
64.Lin, K., Dorman, J. B., Rodan, A., and Kenyon, C.
(1997) daf-16: an HNF-3/forkhead family member that can function to
double the life-span of Caenorhabditis elegans, Science,
278, 1319-1322.
65.Boehm, M., and Slack, F. (2005) A developmental
timing microRNA and its target regulate life span in C. elegans,
Science, 310, 1954-1957.
66.Hsu, A. L., Murphy, C. T., and Kenyon, C. (2003)
Regulation of aging and age-related disease by DAF-16 and heat-shock
factor, Science, 300, 1142-1145.
67.Uno, M., and Nishida, E. (2016)
Lifespan-regulating genes in C. elegans, Aging Mech.
Dis., 2, 16010.
68.Friedman, D. B., and Johnson, T. E. (1988) Three
mutants that extend both mean and maximum life span of the nematode,
Caenorhabditis elegans, define the age-1 gene, J.
Gerontol., 43, 102-109.
69.Ogg, S., Paradis, S., Gottlieb, S., Patterson, G.
I., Lee, L., Tissenbaum, H. A., and Ruvkun, G. (1997) The Fork head
transcription factor DAF-16 transduces insulin-like metabolic and
longevity signals in C. elegans, Nature, 389,
994-999.
70.Henderson, S. T., and Johnson, T. E. (2001)
Daf-16 integrates developmental and environmental inputs to mediate
aging in the nematode Caenorhabditis elegans, Curr.
Biol., 11, 1975-1980.
71.Murphy, C. T., McCarroll, S. A., Bargmann, C. I.,
Fraser, A., Kamath, R. S., Ainger, J., Li, H., and Kenyon, C. (2003)
Genes that act downstream of DAF-16 to influence the lifespan of
Caenorhabditis elegans, Nature, 424, 277-283.
72.Shaw, W. M., Luo, S., Landis, J., Asaf, J., and
Murphy, C. T. (2007) The C. elegans TGF-beta Dauer pathway
regulates longevity via insulin signaling, Curr. Biol.,
17, 1635-1645.
73.Li, W., Gao, B., Lee, S. M., Bennett, K., and
Fang, D. (2007) RLE-1, an E3 ubiquitin ligase, regulates C.
elegans aging by catalyzing DAF-16 polyubiquitination, Dev.
Cell, 12, 235-246.
74.Heimbucher, T., Liu, Z., Bossard, C., McCloskey,
R., Carrano, A. C., Riedel, C. G., Tanasa, B., Klammt, C., Fonslow, B.
R., Riera, C. E., Lillemeier, B. F., Kemphues, K., Yates, J. R., 3rd,
O’Shea, C., Hunter, T., and Dillin, A. (2015) The deubiquitylase
MATH-33 controls DAF-16 stability and function in metabolism and
longevity, Cell Metab., 22, 151-163.
75.Tullet, J. M., Hertweck, M., An, J. H., Baker,
J., Hwang, J. Y., Liu, S., Oliveira, R. P., Baumeister, R., and
Blackwell, T. K. (2008) Direct inhibition of the longevity-promoting
factor SKN-1 by insulin-like signaling in C. elegans,
Cell, 132, 1025-1038.
76.Tepper, R. G., Asaf, J., Kaletsky, R., Kleemann,
G., Murphy, C. T., and Bussemaker, H. J. (2013) PQM-1 complements
DAF-16 as a key transcriptional regulator of DAF-2-mediated development
and longevity, Cell, 154, 676-690.
77.Wolkow, C. A., Kimura, K. D., Lee, M. S., and
Ruvkun, G. (2000) Regulation of C. elegans lifespan by
insulin-like signaling in the nervous system, Science,
290, 147-150.
78.Wullschleger, S., Loewith, R., and Hall,
M. N. (2006) TOR signaling in growth and metabolism, Cell,
124, 471-484.
79.Vellai, T., Takacs-Vellai, K., Zhang, Y., Kovacs,
A. L., Orosz, L., and Muller, F. (2003) Genetics: influence of TOR
kinase on lifespan in C. elegans, Nature, 426,
620-627.
80.Chen, D., Li, P. W.-L., Goldstein, B. A.,
Goldstein, B. A., Cai, W., Thomas, E. L., Chen, F., Hubbard, A. E.,
Melov, S., and Kapahi, P. (2013) Germline signaling mediates the
synergistically prolonged longevity produced by double mutations in
daf-2 and rsks-1 in C. elegans, Cell Rep., 5,
1600-1610.
81.Berdichevsky, A., Viswanathan, M., Horvitz, H.
R., and Guarente, L. (2006) C. elegans SIR-2.1 interacts with
14-3-3 proteins to activate DAF-16 and extend life span, Cell,
125, 1165-1177.
82.Apfeld, J., O’Connor, G., McDonagh, T.,
DiStefano, P. S., and Curtis, R. (2004) The AMP-activated protein
kinase AAK-2 links energy levels and insulin-like signals to lifespan
in C. elegans, Genes Dev., 18, 3004-3009.
83.Greer, E. L., Maures, T. J., Ucar, D., Hauswirth,
A. G., Mancini, E., Lim, J. P., Benayoun, B. A., Shi, Y., and Brunet,
A. (2011) Transgenerational epigenetic inheritance of longevity in
Caenorhabditis elegans, Nature, 479, 365-371.
84.Jin, C., Li, J., Green, C. D., Yu, X., Tang, X.,
Han, D., Xian, B., Wang, D., Huang, X., Cao, X., Yan, Z., Hou, L., Liu,
J., Shukeir, N., Khaitovich, P., Chen, C. D., Zhang, H., Jenuwein,
T., and Han, J. D. (2011) Histone demethylase UTX-1 regulates C.
elegans life span by targeting the insulin/IGF-1 signaling pathway,
Cell Metab., 14, 161-172.
85.Smith-Vikos, T., De Lencastre, A., Inukai, S.,
Shlomchik, M., Holtrup, B., and Slack, F. J. (2014) MicroRNAs mediate
dietary-restriction-induced longevity tough PHA-4/FOXA and SKN-1/Nrf
transcription factors, Curr. Biol., 24, 2238-2246.
86.Zhang, Y., Shao, Z., Zhai, Z., Shen, C., and
Powell-Coffman, J. A. (2009) The HIF-1 hypoxia-inducible factor
modulates lifespan in C. elegans, PLoS One, 4,
e6348.
87.Leiser, S. F., Miller, H., Rossner, R., Rossner,
R., Fletcher, M., Leonard, A., Primitivo, M., Rintala, N., Ramos,
F. J., Miller, D. L., and Kaeberlein, M. (2015) Cell nonautonomous
activation of flavin-containing monooxygenase promotes longevity and
health span, Science, 350, 1375-1378.
88.Walker, G., Houthoofd, K., Vanfleteren, J. R.,
and Gems, D. (2005) Dietary restriction in C. elegans: from
rate-of-living effects to nutrient sensing pathways, Mech. Ageing
Dev., 126, 929-937.
89.McColl, G., Rogers, A. N., Alavez, S.,
Hubbard, A. E., Melov, S., Link, C. D., Bush, A. I., Kapahi, P., and
Lithgow, G. J. (2010) Insulin-like signaling determines survival during
stress via posttranscriptional mechanisms in C. elegans, Cell
Metab., 12, 260-272.
90.Oliveira, R. P., Porter Abate, J., Dilks, K.,
Landis, J., Asaf, J., Murphy, C. T., and Blackwell, T. K. (2009)
Condition-adapted stress and longevity gene regulation by
Caenorhabditis elegans SKN-1/Nrf, Aging Cell,
8, 524-541.
91.Kirstein, J., Morito, D., Kakihana, T., Sugihara,
M., Minnen, A., Hipp, M. S., Nussbaum-Krammer, C., Kasturi, P., Hartl,
F. U., Nagata, K., and Morimoto, R. I. (2015) Proteotoxic stress and
ageing triggers the loss of redox homeostasis across cellular
compartments, EMBO J., 34, 2334-2349.
92.Vilchez, D., Simic, M. S., and Dillin, A. (2014)
Proteostasis and aging of stem cells, Trends Cell Biol.,
24, 161-170.
93.Atlan, H., Miquel, J., Helmle, L. C., and Dolkas,
C. B. (1976) Thermodynamics of aging in Drosophila melanogaster,
Mech. Ageing Dev., 5, 371-387.
94.Markov, A. V., Naimark, E. B., and Yakovleva, E.
U. (2016) Temporal scaling of age-dependent mortality: dynamics of
aging in Caenorhabditis elegans is easy to speed up or slow
down, but its overall trajectory is stable (Commentary to the paper by
Stroustrup et al. (2016) Nature, 530, 103-107),
Biochemistry (Moscow), 81, 1148-1155.
95.Asgharian, H., Chang, P. L., Lysenkov, S.,
Scobeyeva, V. A., Reisen, W. K., and Nuzhdin, S. V. (2015) Evolutionary
genomics of Culex pipiens: global and local adaptations
associated with climate, life-history traits and antopogenic factors,
Proc. Biol. Sci., 282, 20150728.
96.Akaike, A. (1974) A new look at the statistical
model identification, IEEE Trans. Autom. Control., 19,
716-723.
97.Gavrilova, N. S., Gavrilov, L. A., Severin,
F. F., and Skulachev, V. P. (2012) Testing predictions of the
programmed and stochastic theories of aging: comparison of variation in
age at death, menopause, and sexual maturation, Biochemistry
(Moscow), 77, 754-760.
98.Austad, S. N. (2004) Is aging programmed?
Aging Cell, 3, 249-251.
99.Gladyshev, V. N. (2013) The origin of aging:
imperfectness-driven non-random damage defines the aging process and
control of lifespan, Trends Genet., 29, 506-512.
100.Mitnitski, A., and Rockwood, K. (2016) The rate
of aging: the rate of deficit accumulation does not change over the
adult life span, Biogerontology, 17, 199-204.
101.Khokhlov, A. N. (2010) Does aging need an
own program or the existing development program is more than enough,
Russ. J. Gen. Chem., 80, 1507-1513.
102.Blagosklonny, M. V. (2007) Program-like aging
and mitochondria: instead of random damage by free radicals, J.
Cell. Biochem., 102, 1389-1399.
103.Goldsmith, T. C. (2008) Aging, evolvability,
and the individual benefit requirement; medical implications of aging
theory controversies, J. Theor. Biol., 252, 764-768.
104.Libertini, G. (2008) Empirical evidence for
various evolutionary hypotheses on species demonstrating increasing
mortality with increasing chronological age in the wild, Sci. World
J., 8, 182-193.
105.Curtis, R., O’Connor, G., and DiStefano,
P. S. (2006) Aging networks in Caenorhabditis elegans:
AMP-activated protein kinase (aak-2) links multiple aging and
metabolism pathways, Aging Cell, 5, 119-126.
106.Jenkins, N. L., McColl, G., and Lithgow,
G. J. (2004) Fitness cost of extended lifespan in Caenorhabditis
elegans, Proc. Biol. Sci., 271, 2523-2526.
107.Fang, X., Seim, I., Huang, Z., Gerashchenko, M.
V., Xiong, Z., Turanov, A. A., Zhu, Y., Lobanov, A. V., Fan, D, Yim, S.
H., Yao, X., Ma, S., Yang, L., Lee, S. G., Kim, E. B., Bronson, R. T.,
Sumbera, R., Buffenstein, R., Zhou, X., Krogh, A., Park, T. J., Zhang,
G., Wang, J., and Gladyshev, V. N. (2014) Adaptations to a
subterranean environment and longevity revealed by the analysis of mole
rat genomes, Cell. Rep., 8, 1354-1364.