
ФУРЬЕ МОДЕЛИ И ПРОГНОЗИРОВАНИЕ
ВРЕМЕННЫХ РЯДОВ
г
Кулаичев А.П., 1995
ссылки при цитировании:
Кулиичев. Методы и средства комплексного анализа данных. ИНФРА-М, 2006,
512 с, С.260-272

Назначение.
Данный метод разработан нами в 1995 г. как средство моделирования нестационарных
временных рядов, имеющих выраженные гармонические составляющие. Фурье–модели,
в отличие от большинства других, являются многоцелевым инструментом и могут
применяться как для прогнозирования, так и для интерполяции, фильтрации
и сглаживания временных рядов.
Что касается прогнозирования, то основной
творческой задачей является учет в модели детерминированной компоненты,
присутствующей во временном ряду, и отбрасывание случайной компоненты или
шума, который будет определять не среднее прогнозируемое значение, а его
доверительный интервал. И для решения этой задачи фурье–модели предлагают
логичную и понятную основу, в отличие, например, от ARIMA–моделей, где
подбор значений параметров осуществляется часто простым перебором комбинаторики.
Метод.
Рассматриваемый метод основан на Фурье–преобразовании из временной области
в частотную область (получение амплитудно–частотной АЧХ и фазочастотной
ФЧХ характеристик) и обратно (восстановление исходного временного ряда
по АЧХ и ФЧХ). Большим преимуществом Фурье–преобразования является то,
что оно сохраняет всю информацию о процессе, а спектральное представление
позволяет осознанно и осмысленно решить, какие гармонические составляющие
по величине их амплитуд следует отнести к случайным, шумовым компонентам,
а какие к закономерным. И если обратное преобразование полного спектра
однозначно восстанавливает временной ряд, а любой прогноз является точным
повторением временного ряда с его начала, то после удаления шумовых гармоник
из АЧХ и ФЧХ обратное преобразование уже не будет стопроцентно повторять
временной ряд, а адаптация (приближение) усеченной таким образом модели
к временному ряду в частотной области делает и сам прогноз неповторяющимся.
Кроме того, в данную процедуру введены
средства учета (удаление–восстановление) тренда и скачков процесса, что
позволяет ее применять напрямую к исходным временным рядам без их предварительных
чисток, центрирования и нормирования.
Методика.
Предварительные преобразования позволяют скорректировать временной ряд,
удалив из него тренд и скачки. Основными инструментами построения спектральной
модели скорректированного подобным образом ряда являются:
1) экспоненциальное усреднение его спектральных
характеристик;
2) последовательная фильтрация — удаление
из спектра всех составляющих в заданном диапазоне частот;
3) очистка спектра — удаление из него всех
низкоамплитудных гармонических составляющих, не превышающих заданный уровень;
4) адаптация усеченной таким образом спектральной
модели.
Эти инструменты являются взаимодополняющими и их можно использовать
независимо или же в произвольных комбинациях друг с другом.
Усреднение.
Для усреднения задается число последовательных делений временного ряда.
Каждое деление определяет отрезок, вдвое короче предыдущего и примыкающий
к концу временного ряда. При первом делении временной ряд разбивается пополам
и берется последний отрезок. При втором делении временной ряд делится на
четыре части и берется последний отрезок и так далее. На каждом отрезке
независимо вычисляются частотные характеристики и производится их экспоненциальное
усреднение, т. е. последующие отрезки имеют и большие веса. В результате
в спектре в большей степени проявляются высокочастотные составляющие, характерные
для временных отрезков, близлежащих к настоящему (к конечной точке временного
ряда), с сохранением длинноволновых составляющих.
Адаптация
модели осуществляется посредством последовательного приближения
к временному ряду по критерию наименьших квадратов трех параметров (амплитуда,
фаза, частота) каждой ненулевой спектральной составляющей модели. Каждый
из трех параметров итерационным образом изменяется так, чтобы достигнуть
максимального приближения модели к временному ряду. Именно адаптация по
частоте приводит к неповторению в прогнозе начала модели временного ряда.
Фильтрацию и очистку спектра можно произвести
несколько раз при нулевом прогнозе.
Действия
и результаты. Если в электронной таблице содержится несколько
переменных, то нужно выбрать представляющую анализируемый временной ряд
(см. бланк рис. 6.4). Последующие действия и результаты включают следующие
шаги.
Рис. 6.1
1. Предварительная коррекция процесса.
Выделению гармонических составляющих и выбору параметров спектральной модели
часто мешает наличие в процессе тренда и высокоамплитудных, непериодических
скачков (в литературе используется также термин «интервенции»). Удаление
этих компонентов производится установками меню (рис. 9.33). Произведенные
коррекции будут автоматически восстановлены при прогнозировании временного
ряда.
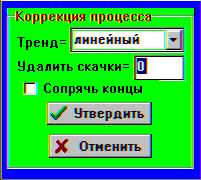
Рис. 9.33. Бланк коррекции процесса
|
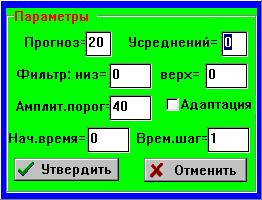
Рис. 9.34. Бланк параметров фурье–модели
|
Для нивелирования тренда предлагаются две
модели: линейная и параболическая. Применимость той или иной модели может
быть предварительно оценена методом простой регрессии (разд. 10.2) с доступным
там же прогнозированием. Следует подчеркнуть, что линейная модель часто
является более предпочтительной, несмотря на отклонения процесса от линейности,
поскольку эти отклонения будут автоматически учтены спектральной моделью.
Скачки характеризуются экстраординарным
значением производной (скорости изменения процесса). Для их удаления в
поле ввода бланка рис. 9.32 следует задать уровень «нормальных» значений
производной. Оценить этот уровень можно, вычислив предварительно производную
и посмотрев на ее график (методом дифференцирования из разд. 9.4). Для
более точной оценки полезно сохранить данные с графика в электронной таблице
(кнопка «СохрГраф») и там изучить значения производной в цифровом виде.
При нулевом значении уровня производной скачки не удаляются.
Для процессов монотонного характера полезно
дополнительно установить режим «сопряжения концов», который состоит в повторном
удалении «псевдотренда» так, чтобы начальные и конечные амплитуды скорректированного
процесса совпадали, иначе при прогнозировании может наблюдаться скачок
в начале прогноза (вследствие математических свойств Фурье–преобразования).
Для процессов с высокочастотными колебаниями сопряжение концов не обязательно,
а иногда и нежелательно.
График скорректированного временного ряда
выдается для визуальной оценки и изучения. При неудовлетворительном результате
коррекцию можно повторить.
2. Оценочный график АЧХ. Оценку гармонических
составляющих процесса для принятия решения о разделении детерминированных
и шумовых составляющих легко произвести по графику амплитудно–частотной
характеристики или амплитудного спектра (см. разд. 9.3). Шкала амплитуд
на графике для удобства представлена в процентах от максимальной амплитуды.
3. Параметры модели. После этого
уже можно осмысленно определить необходимые параметры фурье–модели (бланк
рис. 9.34):
– число шагов прогноза развития процесса (при нулевом значении этого
параметра прогноз не строится);
– число делений временного ряда для экспоненциального усреднения
спектра; значение 1 соответствует усреднению спектра со спектром отрезка
в 1/2 длины временного ряда от его конца, значение 2 — с отрезками 1/2
и 1/4 длины временного ряда и т. д. (при значении 0 усреднение не производится,
на длине отрезка менее 8 отсчетов усреднение автоматически завершается,
поэтому строго контролировать верхний предел этого значения не требуется);
– верхняя и нижняя границы диапазона частот удаляемых спектральных
составляющих (фильтрация), при нулевых значениях фильтрация не производится;
– амплитудный порог, ниже которого удаляются все спектральные составляющие
(при нулевом значении удаление не производится);
– признак необходимости адаптации усеченной модели к временному
ряду (при отсутствии признака адаптационный механизм не запускается, для
полной спектральной модели адаптация эффекта не имеет);
– начальное время процесса и его временной шаг необходимы только
для временной шкалы результатов прогнозирования, во всех других результатах
время без ущерба для общности представляется последовательностью натуральных
чисел.
Нажатие на кнопку «Утвердить» продолжает
дальнейший анализ в соответствии с установленными параметрами, а нажатие
на кнопку «Отменить» приводит к завершению работы процедуры.
Нулевые значения параметров соответствуют чистой
фурье-модели, точно воспроизводящей временной ряд.
Продолжение анализа зависит от наличия или отсутствия
заказа прогнозирования.
4. Результаты без прогноза. В случае
отсутствия прогнозирования в качестве числовых результатов выдается последовательность
значений временной модели анализируемого ряда и среднеквадратичного шума
(характеризует отличие модели от исходного временного ряда), а также совместный
график скорректированного временного ряда и его фурье–модели, т. е. без
восстановления тренда и скачков). Для визуализации модели исходного временного
ряда следует фиктивно заказать один шаг прогноза.
Далее по подтверждению можно возвратиться
к новым установкам параметров модели. Такой цикл позволяет последовательно
удалять из модели отдельные спектральные составляющие.
5. Анализ остатков. В случае наличия
прогноза по подтверждению может быть произведен анализ остатков, т. е.
разностей между моделью и временным рядом. В качестве числовых результатов
выдается таблица значений следующих показателей (аналогично методу простой
регрессии, см. разд. 10.1):
X Yэксп Yмодл остаток
Ст.остат Ст.ошиб Довер.инт
Затем выдается график регрессионных остатков для последовательных точек
временного ряда.
6. Прогноз. Выдается таблица параметров
фурье–модели, включающая следующие значения:
Амплитуда Период Фаза
Затем выдается таблица прогноза, включающая значения следующих показателей
(аналогично методу простой регрессии, см. разд. 10.1):
Xпрогн Yпрогн Ст.ошиб
Довер.инт
В завершение выдается график временного ряда, совмещенный с графиком
временной модели с зоной прогноза. В зоне прогноза указаны верхняя и нижняя
границы доверительного интервала прогнозируемых значений.
Полученные результаты можно перенести
в электронную таблицу для последующего анализа и построения комплексных
графиков с числовой выдачи результатов посредством буфера обмена (Clipboard)
или напрямую с графиков нажатием инструментальной кнопки «СохрГраф».
П р и м е р 1
З а д а ч а. Данный пример предназначен
для сравнения фурье–моделей с другими методами анализа временных рядов.
Поэтому в качестве исходных данных используем хорошо знакомый в данной
главе временной ряд изменения авиаперевозок (см. рис. 9.9). Внимательное
изучение исходного временного ряда показывает, что в нем с течением времени
нарастают амплитуды высокочастотных нерегулярных составляющих, существенно
искажающие главный годичный ритм (нестационарность).
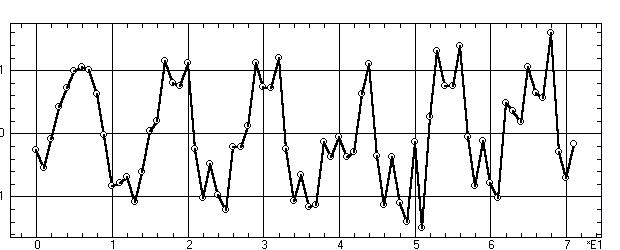
Рис. 9.9
Ш а г 1. Поскольку временной ряд уже
нормирован и центрирован предварительная коррекция модели (тренд, скачки)
не нужна. Амплитудный спектр процесса приведен на рис. 9.10.
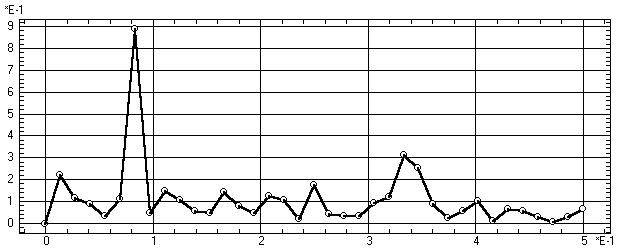
Рис. 9.10
Для начала произведем только фильтрацию высокочастотных составляющих
спектра в диапазоне от 20 до 36. Для этого в бланке параметров фурье–модели
(рис. 9.34) следует заполнить позиции верхнего и нижнего фильтров, остальные
позиции оставим нулевыми.
Р е з у л ь т а т ы:
ФУРЬЕ-МОДЕЛИ Файл: spec1.std Переменная
flight Ст.откл.шума=0.343
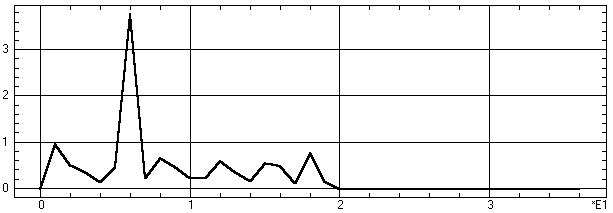
Рис. 9.35. График спектральной модели после удаления высокочастотных
составляющих
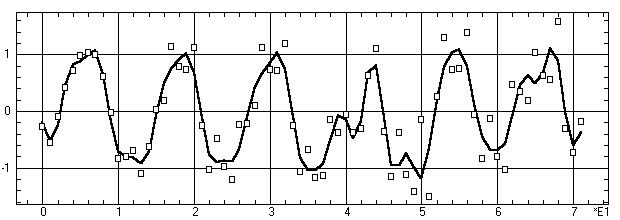
Рис. 9.36. График фильтрации временного ряда авиаперевозок
Обсуждение: В результате фильтрации
спектр процесса приобрел вид рис. 9.35. Как можно видеть по графику результата
фильтрации (рис. 9.36), удаление высокочастотных составляющих из спектра
действительно привело к желаемому сглаживанию быстрых колебаний временного
ряда. Полученный результат близок к результату фильтрации ряда скользящим
средним (см. рис. 9.24). Удаленные компоненты соответствуют шуму (характеризует
различие между моделью и временным рядом) со стандартным отклонением 0,343.
Ш а г 2. Удалим теперь из спектра
основную спектральную гармонику (сезонный компонент) в диапазоне частот
4–8.
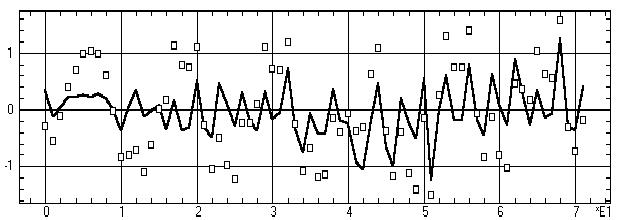
Рис. 9.37. График спектральной модели после сезонной фильтрации
Обсуждение: Сравним полученный результат
(рис 9.37) с результатом сезонной фильтрации из разд. 9.4 (см. рис. 9.27).
Как можно заметить, фурье–фильтрация обеспечивает удаление сезонной составляющей
без резких выбросов, характерных для рис. 9.27, кроме того результат охватывает
всю длину временного ряда, без присущего сезонному дифференцированию «обрезания»
конца ряда.
Ш а г 3. Используем теперь нефильтрованную
(«чистую») фурье–модель для прогнозирования авиаперевозок на 30 шагов,
т. е. на два с половиной года. Для этого в бланке рис. 9.34 заполним только
поле прогноза.
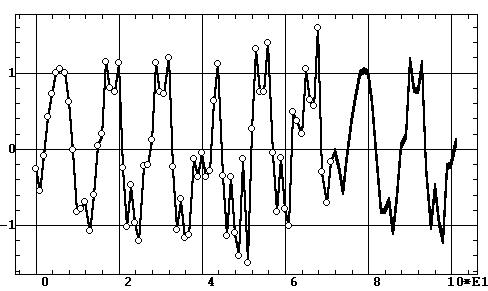
Рис. 9.38. Временной ряд авиаперевозок с прогнозом на 30 шагов
Обсуждение: Как видно из полученного
результата (рис 9.38), чистая фурье–модель полностью повторяет временной
ряд и ее прогноз является повторением начального участка процесса.
Ш а г 4. Изменим модель, удалив
из спектра малоамплитудные составляющие, не превышающие 15% от максимума.
Р е з у л ь т а т ы (сокращенно):
Файл: spec1.std Переменная flight
Параметры Фурье–модели
Амплитуда Период Фаза
0.00571
0 180
0.217
73 -9.34
0.894
12.2 161
0.145
9.13 -38.8
0.145
6.08 -105
0.172
4.06 -15
0.313
3.04 71.3
0.258
2.92 -152
Ст.отклонение остатков (различие модели и процесса)=0.0817
X Yэксп
Yмодл остаток Ст.остат Ст.ошиб Довер.инт
0 -0.256
-0.457 0.202 0.706
0.296 0.582
1 -0.537
-0.212 -0.325 -1.12 0.295
0.581
2 -0.081
-0.166 0.0851 0.301 0.295
0.58
3 0.432
0.279 0.153 0.538
0.295 0.58
4 0.737
0.658 0.0789 0.279 0.294
0.579
5
1.01 0.659 0.347
1.21 0.294 0.579
6
1.06 0.963 0.097
0.342 0.294 0.578
7
1.02 1.25 -0.234 -0.807
0.294 0.578
8 0.635
0.786 -0.151 -0.519 0.293
0.577
9 -0.00816 -0.0947
0.0865 0.306 0.293
0.577
10 -0.822
-0.511 -0.311 -1.08 0.293
0.576 . . .
Xпрогн Yпрогн Ст.ошиб
Довер.инт
72 -0.457
0.296 0.582
73 -0.212
0.296 0.583
74 -0.166
0.297 0.584
75 0.279
0.297 0.584
76 0.658
0.297 0.585
77 0.659
0.298 0.586
78 0.963
0.298 0.587
79
1.25 0.298 0.587
80 0.786
0.299 0.588
. . .
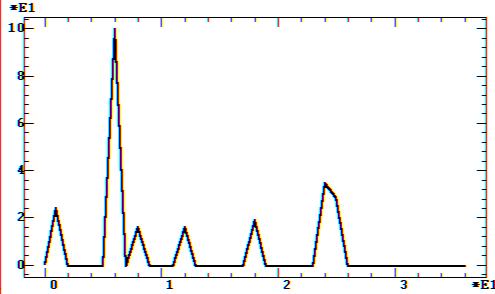
Рис. 9.39. График спектральной модели после удаления малоамплитудных
составляющих
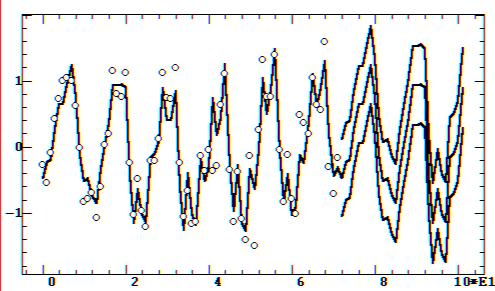
Рис. 9.40. Временной ряд авиаперевозок с фурье–моделью и с прогнозом
на 30 шагов
Обсуждение: Здесь с иллюстративными
целями приведена также и числовая выдача результатов с параметрами модели,
анализом остатков и прогнозом. Амплитудный спектр модели приведен на рис.
9.39.
Как видно из результата моделирования и
прогноза (рис 9.40), модель уже не повторяет временной ряд. По сравнению
с рис. 9.38 появились высокочастотные колебания на начальном участке процесса,
но снизилась их амплитуда на конечном участке. Однако прогноз остается
повторением начального участка смоделированного ряда.
Ш а г 5. Добавим к данной модели
еще и адаптацию.
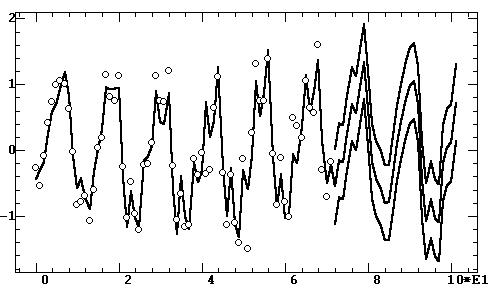
Рис. 9.41. Фурье–модель с адаптацией
Обсуждение: Как видно из рис 9.41 за
счет адаптации само моделирование процесса по сравнению с рис. 9.40 более
близко к чистой фурье–модели (см. рис. 9.38) и к исходному временному ряду,
к тому же прогноз уже не повторяет начало временного ряда.
Ш а г 6. Добавим теперь в модель
еще и два усреднения.
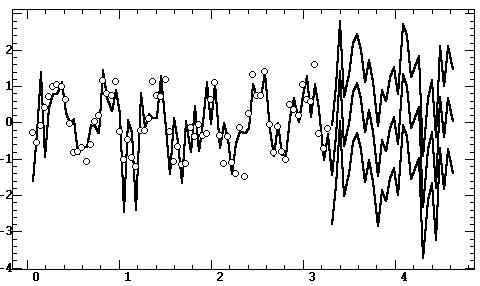
Рис. 9.42. Фурье–модель с адаптацией и двумя усреднениями
Обсуждение: Как видно из рис 9.42 за
счет усреднения по сравнению с рис. 9.41 в зоне прогнозирования более представлены
высокочастотные колебания, характерные для последнего участка временного
ряда. Поэтому в отношении прогноза эту модель следует признать более адекватной,
хотя при моделировании начального участка авиаперевозок там появились не
характерные для него высокочастотные колебания.
С р а в н е н и е
м е т о д о в
З а д а н и е: Проведем сравнение предложенного
фурье–метода с авторегрессионным подходом (разд. 9.5). Для этого исключим
из рассматриваемого временного ряда его последнюю треть и сравним точность
прогнозирования на этом участке, достигаемую с использованием каждого метода
(рис. 9.38). Для фурье–модели используем уже опробованную схему двукратного
усреднения с адаптацией и очисткой спектра.
Р е з у л ь т а т ы:
X Y
Yфурье Yarima
50 -0.1187 -0.861 -0.151
51 -1.482 0.281
-0.0169
52 0.2741 0.383
-0.0822
53 1.321 -0.0206
0.824
54 0.7636 0.453
0.769
55 0.7658 1.33
0.199
56 1.405 1.16
0.373
57 -4.042E-2 0.176 0.047
58 -0.8149 -0.457 -0.62
59 -0.1097 -0.869 -0.505
60 -0.7781 -1.63
-0.464
61 -1.003 -1.89
-0.661
62 0.4955 -0.778
-0.27
63 0.3761 0.543
0.0779
64 0.2025 0.623
0.0485
65 1.06 0.141
0.272
66 0.6503 0.375
0.403
67 0.5779 0.817
0.139
68 1.603 0.484
0.0277
69 -0.2873 -0.0613 -0.0376
70 -0.7006 -0.0925 -0.311
71 -0.1595 -0.361 -0.385
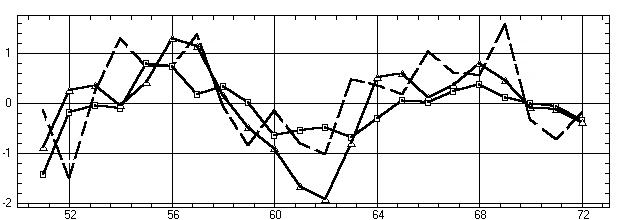
Рис. 9.43. Сравнение фурье–прогноза (треугольники) и ARIMA–прогноза
(квадраты) с временным рядом авиаперевозок (пунктирная линия)
Обсуждение: В числовых результатах выше
приведены истинные значения прогнозируемого временного ряда Y и прогностические
значения фурье– и ARIMA–моделей; Yфурье, Yarima. Для количественного сравнения
обоих методов вычислим среднее стандарт-ное отклонение S для разностей
между прогностическими и истинными значениями (Y–Yфурье, Y–Yarima) и получим:
S=0,578 для фурье–модели и S=0,641 для ARIMA–модели.
Таким образом фурье–модель дает прогноз
в среднем на 9,8%=(0,641–0,578)/0,641*100 точнее, чем широко популярная,
но алго-ритмически неизмеримо более сложная и трудная для понимания ARIMA–модель.
Заключение: На основании выводов
по рассмотренным примерам можно сделать следующий вывод: предложенные фурье–модели
являются многоцелевым инструментом исследования и в каждой из своих областей
при-менения дают результаты не хуже, а зачастую – и лучше, чем по-пулярные
и давно известные аналоги.
П р и м е р 2
З а д а ч а. Попробуем смоделировать
и спрогнозировать натуральный (непреобразованный) временной ряд изменения
урожайности зерновых в СССР из примера 1 к разд. 10.3.
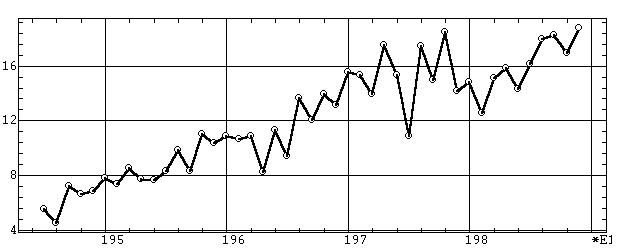 Поскольку, как там показано, для этого ряда более подходит параболическая
модель тренда по сравнению с линейной, то для сравнения используем обе
эти модели. Кроме того в этом процессе не наблюдается явных скачков, что
следует из самой природы процесса (примеры с удалением скачков рассмотрены
разд. 14.4).
Поскольку, как там показано, для этого ряда более подходит параболическая
модель тренда по сравнению с линейной, то для сравнения используем обе
эти модели. Кроме того в этом процессе не наблюдается явных скачков, что
следует из самой природы процесса (примеры с удалением скачков рассмотрены
разд. 14.4).
Р е з у л ь т а т ы (сокращенно
и без числовой выдачи):
а — полиномиальный тренд
|
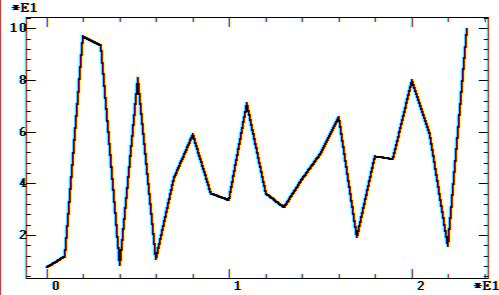
б — полиномиальный тренд
|
Рис. 9.44. Спектры изменения урожайности зерновых после
удаления тренда:
Обсуждение: Как видно из графиков полных
спектральных моделей (рис. 9.44) малозначимые компоненты можно отсечь на
уровне 30% от амплитуды максимальной гармоники. В связи с небольшой длиной
временного ряда выполним только два усреднения с адаптацией, дополнительной
фильтрации делать не будем, выполним прогноз изменения урожайности зерновых
на 20 лет вперед, т. е. до 2009 г.
Р е з у л ь т а т ы (сокращенно
и без числовой выдачи):
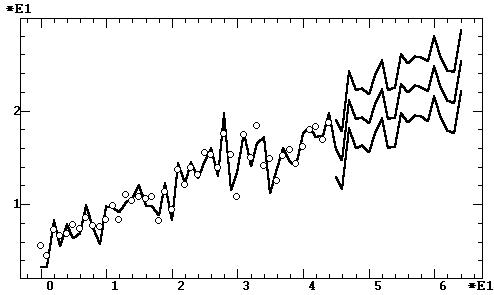
а — линейный тренд
|
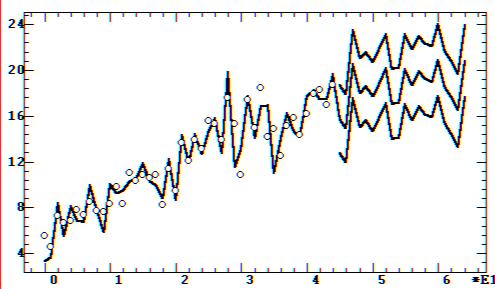
б — полиномиальный тренд
|
Рис. 9.45. Модель и прогноз урожайности зерновых в СССР:
Обсуждение: Как видно из графиков моделей
и прогнозов, параболическая модель (рис. 9.45) предсказывает в среднем
практически полную стагнацию урожайности на 20 лет. Линейная же модель
(рис. 9.45, а) предсказывает в среднем рост приблизительно линейного характера,
на котором, однако, внимательным взглядом можно заметить продолжение замедления
роста, характерное для последней трети процесса. Тем самым линейную модель
тренда в данном случае следует признать более адекватной средним тенденциям
временного ряда. Почему это происходит, несмотря на лучшее соответствие
временного ряда параболической модели, выявленное в примере 1 разд. 10.3.
Как можно заметить из сравнения спектров рис. 9.44 в линейной модели намного
более выражена самая низкочастотная гармоника. И именно она компенсирует
сравнительно меньшую адекватность модели линейного тренда, добавляя к нему
длинно периодическую синусоиду. Это было уже отмечено в основной части
данного раздела.
Еще следует отметить, что обе модели проявляют
существенные высокочастотные колебания урожайности, характерные для последней
половины временного ряда, определенную двумя заказанными в модели усреднениями.
П р и м е р 3
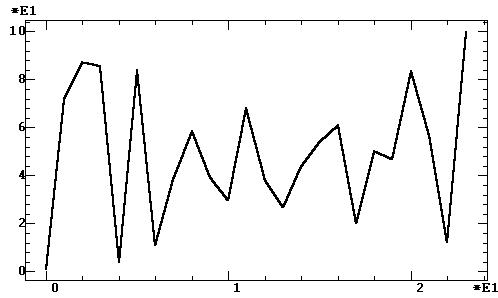
З а д а ч а. Рассмотрим ежемесячную
динамику цен на нефть Брент с 2001 по 2004 гг. (рис. 9.46, файл OIL).
Этот процесс визуально также имеет явную нелинейность, но в отличие от
предыдущего примера не затухающую, а возрастающую. Поэтому здесь также
попробуем сравнить две модели линейную и параболическую. Кроме того, в
этом процессе не наблюдается явных скачков (примеры с удалением скачков
рассмотрены разд. 14.4).
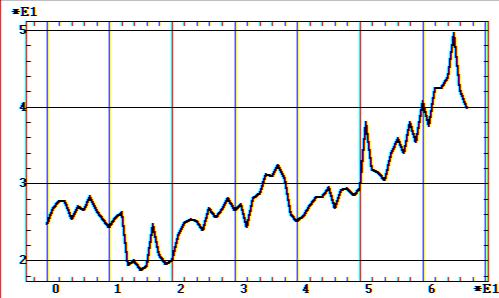
Рис. 9.46. Ежемесячная динамика цен на нефть Брент с 2001 по 2004
гг.
Обсуждение: Как видно из графиков полных
спектральных моделей (рис. 9.47) малозначимые компоненты можно попробовать
отсечь на уровне 10%. При линейном тренде превалирующую амплитуду имеет
низкочастотная составляющая вследствие высокоамплитудных и длинно периодических
колебания остатков относительно тренда. Полиномиальная модель намного более
адекватна процессу и в ней в равной степени представлены низко– и высокочастотные
составляющие. Остальные параметры спектральной модели оставим аналогичными
примеру 2 и выполним прогноз на два последующих года.
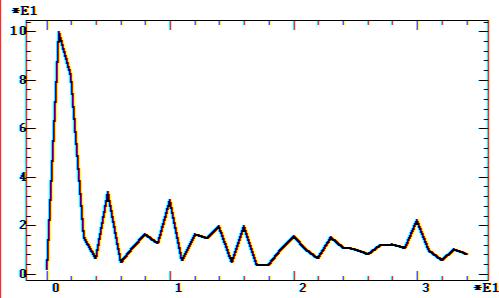
а — линейный тренд
|
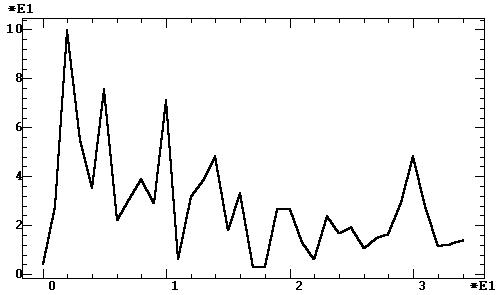
б — полиномиальный тренд
|
Рис. 9.47. Спектры цен на нефть Брент после удаления тренда:
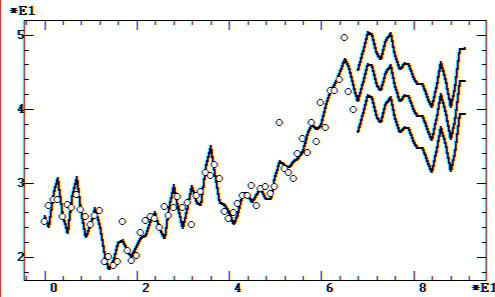
а — линейный тренд
|
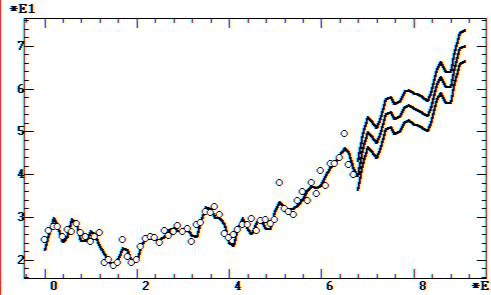
б — полиномиальный тренд
|
Рис. 9.48. Модели и прогнозы цен на нефть Брент:
Обсуждение: Как видно из графиков моделей
и прогнозов, линейная модель (рис. 9.48, а) за счет сильной низковолновой
составляющей в спектре (рис. 9.47, а) предсказывает в снижение цен на нефть
в последующие два года. В противоположенность этому параболическая модель
(рис. 9.48, б) предсказывает продолжение тенденции примерно линейного роста
цен на нефть. Однако из содержательных соображений в начале 2005 г. (т.
е. не имея апостеорной информации) можно было бы сказать, что оба этих
прогноза недостаточно реалистичны, и истина должна лежать где–то посредине.
Возможно, в качестве модели тренда данного процесса более подошла бы парабола
третьей или более высокой степени.
