КОРРЕЛЯЦИОННЫЙ АНАЛИЗ НЕСТАЦИОНАРНЫХ ПРОЦЕССОВ.
ИНТЕРВАЛЬНАЯ И НОМИНАЛЬНАЯ КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
г Кулаичев А.П., 1993
ссылки при цитировании: Кулиичев. Методы и средства комплексного анализа данных. ИНФРА-М, 2006, 512 с, С.222-230

     Назначение. Корреляционный анализ является средством выявления доминирующих корреляций и их лагов (задержек) и периодичностей в одном процессе X (автокорреляция) или между двумя процессами X, Y (кросскорреляция). Высокие корреляции могут служить индикатором причинно-следственных связей или взаимодействий внутри одного процесса или между двумя процессами, а величина лага указывает временную задержку в передаче взаимодействия.
     В случае двух непрерывно изменяющихся сигналов бесконечной протяженности x(t), y(t) корреляционная функция cxy от временного сдвига t определяется интегральным выражением:

 .
Если имеет место равенство y(t)=x(t), то функция называется автокорреляционной.
     Для классического случая стационарных и эргодических временных рядов x(i), y(i), i=1–n, которые являются типичными в физических и технических приложениях, это выражение уточняется следующим образом:
 .
Рис. 1. иллюстрирует вычисление такой корреляционной функции на примере электроэнцефалограммы на эпохе анализа Т.

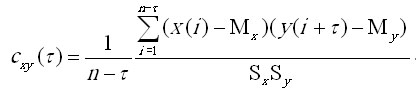
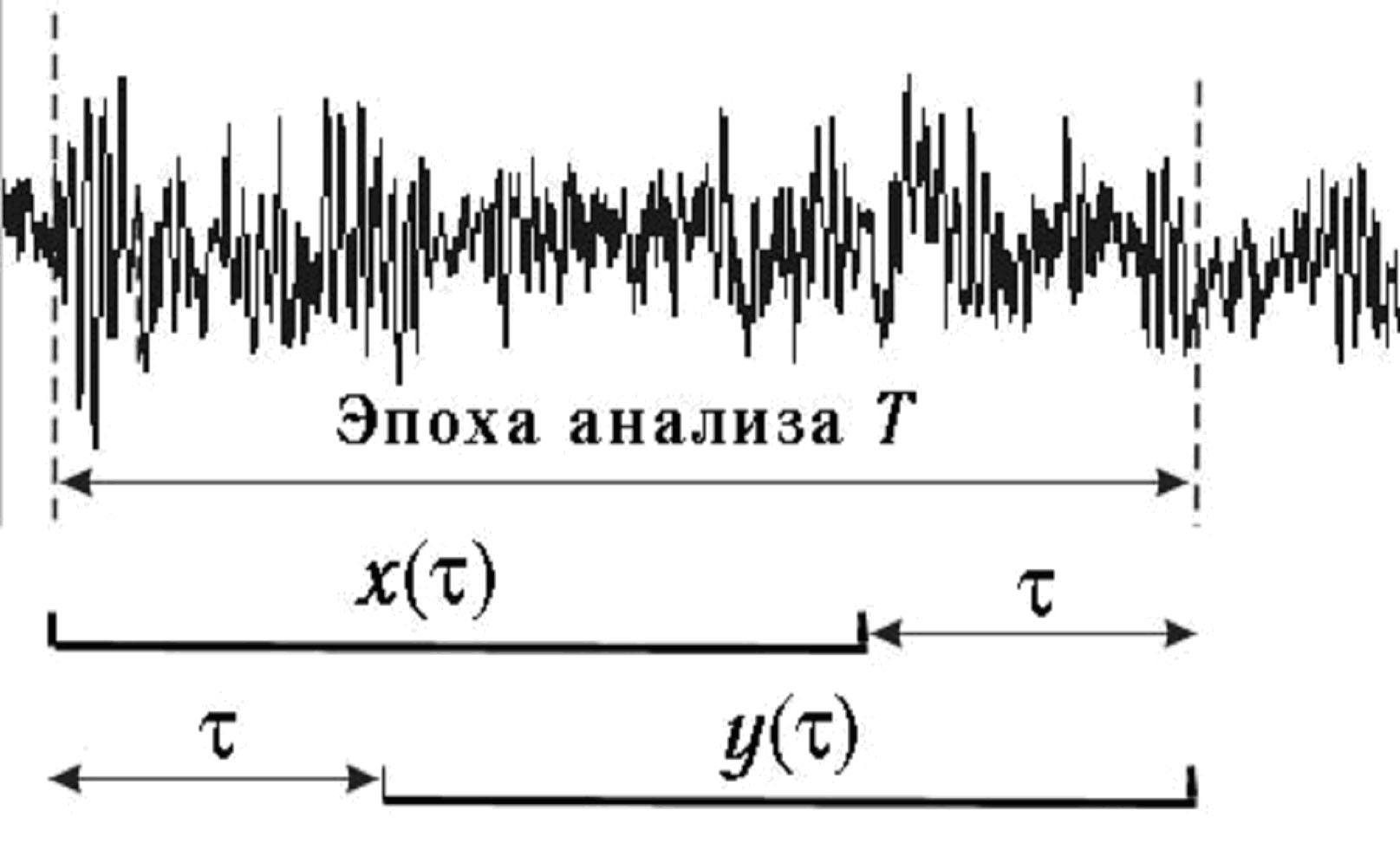
Рис. 1. Вычисление «классической» корреляционной функции

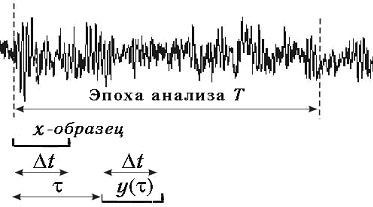
Рис. 2. Вычисление интервальной корреляционной функции

     Недостатки классического анализа. Прежде всего, следует отметить, что в числителе вычисляется ковариация начального отрезка i=1—n-t процесса x(i) и конечного отрезка j=t—n процесса y(j), причем в этих вычислениях используются средние значения Mx, My и стандартные отклонения Sx, Sy, определенные для полноразмерных временных рядов i=1—n. По-видимому, это может быть приемлемо для стационарных временных рядов, статистические свойства которых достаточно стабильны на любых их отрезках. С учетом этих уточнений и ограничений значения cxy(t) напоминают коэффициент корреляции Пирсона.
     Далее, при увеличении временного сдвига t длины отрезков последовательно уменьшаются. Но это уменьшение не может продолжаться до нуля, поэтому встает сложный для однозначного ответа вопрос, на каком t следует заканчивать вычисление корреляционной функции.
     В случае же нестационарных временных рядов классическое определение cxy(t) неприемлемо, поскольку все уменьшающиеся по размеру начальный участок первого ряда; и конечный отрезок второго ряда имеют разные статистические свойства, в частности, средние и стандартные отклонения, поэтому полученные значения корреляционной функции для различных t принципиально несравнимы и неинтерпретируемы. Аналогия с коэффициентом корреляции Пирсона становится очень туманной и отдаленной.

     Практические задачи. Вместе с этим нередко необходимо исследование задержек в передаче воздействия от одного процесса к другому или влияния начального возмущения на последующее развитие того же самого процесса. Например, имеются данные об изменении народонаселения и необходимо выявить повторения в последующих периодах эха от некоторого катастрофического изменения (война, голод, эпидемия и т. п.). Или же пусть имеется некоторая генетическая структура, в середине которой находится известный ген, и требуется определить степень «похожести» всех других участков. Очевидно, что для задач такого типа классический корреляционный анализ также неприменим.
     Для поддержания подобных задач в 1993 нами были предложены две модификации классического метода, названные интервальной и номинальной корреляциями.

     Интервальная корреляция. Интервальная корреляционная функция cxyI(t,i0,m) представляет собой последовательность коэффициентов корреляции Пирсона, вычисленных между фиксированным отрезком первого ряда заданного размера m и начального положения i0 и равноразмерными отрезками второго ряда, выбранных с последовательными сдвигами t от начала ряда.

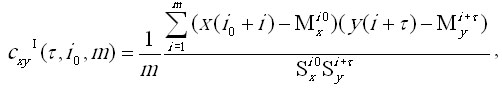
где Mxi0, Myi+t и Sxi0, Syi+t — средние и стандартные отклонения, вычисленные для упомянутых отрезков временных рядов.
     Таким образом, в определение добавляется два новых параметра: длина сдвигаемого фрагмента ряда и его начальное положение, а также используется классическое определение коэффициента корреляции. Благодаря этому, вычисляемые значения становятся сравнимы между собой и просто интерпретируемы.Рис. 2. иллюстрирует вычисление интервальной корреляционной функции на примере электроэнцефалограммы на эпохе анализа Т.

     Номинальная корреляция. Номинальная корреляция cxyN(t,i0,m) является мерой коррелированности номинальных временных рядов (значениями которых являются не числа, а символы). Если при вычислении обычной количественной корреляции для каждой пары значений двух выбранных для анализа переменных вычисляется произведение разностей каждого значения и среднего значения этой переменной, то для номинальной корреляции берется значение единица при совпадении пары значений (символов) и значение ноль при несовпадении пары значений. Примерами подобных рядов могут служить генетические структуры, шифрограммы и т. п.

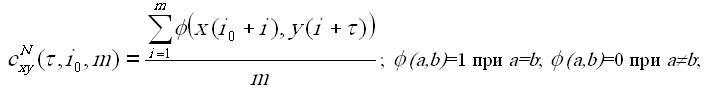
П р и м е р ы

     Сравнение. Различие двух методов вычисления КФ иллюстрирует рис.3.

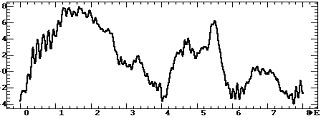
а — классическая

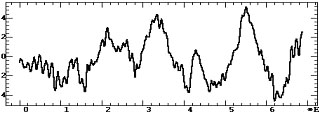
б — интервальная

Рис. 3. Корреляционные функции ЭЭГ-сигнала, приведенного на рис.1,2

     Для классической КФ при небольших сдвигах могут наблюдаться высокие значения вследствие большой длительности отрезков и незначительности их интегральных различий. С увеличением сдвига характерно систематическое уменьшение значений КФ в связи с уменьшением длины отрезков и возрастанием их интегральных различий. Интервальная же КФ периодически повторяет высокие значения при сдвиговых воспроизведениях образца (рис. 2). В отличие от классической КФ для интерпретации динамики интервальной КФ легко найти визуальные основания. Так, например, начальные малые значения КФ на рис. 3б определены резким изменением ритмики сигнала на начальном временном участке рис.1.
     Тем самым интервальная КФ является удобным средством выявления доминирующих корреляций и их лагов (задержек). Высокие корреляции будут наблюдаться тогда, когда при некотором временном сдвиге ритмика участка ЭЭГ будет хорошо повторять ритмику образца. В случае кросскорреляции это может интерпретироваться как задержки в передаче взаимодействия от одного процесса к другому. В случае автокорреляции высокие значения КФ могут интерпретироваться как повторения заданного функционального состояния. В частном же случае корреляционная функция может использоваться для поиска в сигналах заданных характерных образцов.
     Следует подчеркнуть, что коэффициент корреляции и корреляционная функция позволяют отчетливо выявлять степень аутеничности лишь доминирующих (обычно низкочастотных) ритмов, однако это ограничение может быть в значительной степени снято посредством предварительной низкочастотной режекции. Кроме того, этот метод позволяет уловить более быстротечные изменения синхронности двух процессов, чем кросс?спектральные характеристики, поскольку для своего вычисления он допускает значительно более короткие временные отрезки.

     З а д а ч а. Некая коммерческая фирма уделяла важное внимание работе на рынке фьючерсных контрактов. Поэтому для выработки обоснованной стратегии желательно понимание динамики фьючерсного курса и его несомненной связи с текущим курсом доллара. Для этого используются (табл.1) результаты долларовых торгов на ММВБ в период с 3.10.94 по 15.12.94 и результаты фьючерсных долларовых торгов с поставкой 15.12.94 (торги производятся каждый день, исключая субботу и воскресенье).

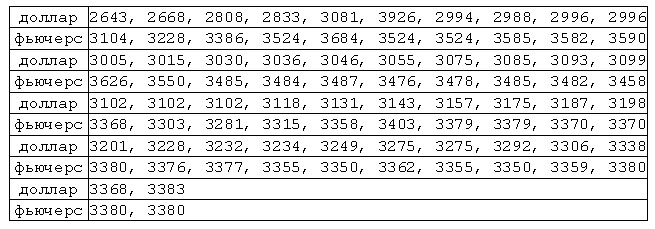
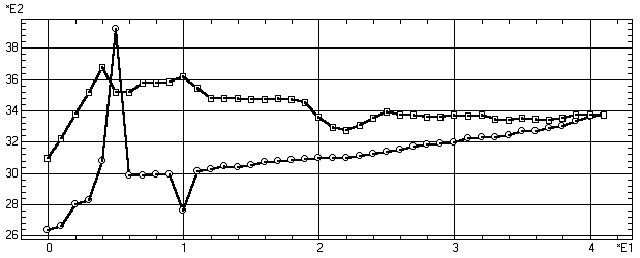
Таблица 1. Результаты долларовых и фьючерсных торгов на ММВБ в период с 3.10.94 по 15.12.94


Рис. 4. Котировка доллара на ММВБ (кресты) и фьючерсных поставок (квадраты) с 3.10 по 15.12 1994 г.

     Визуальный анализ. В курсе доллара (рис. 4) выделяется пик знаменитого «черного вторника» (11.10.94) и линейная тенденция с небольшими колебаниями, отражающая методику «циркуля и линейки», распространенную тогда в высших планирующих органах. Во фьючерсном курсе имеется вполне понятная тенденция приближения к реальному курсу (при приближении дня поставки 15.12.94) с нерегулярными и достаточно высокоамплитудными колебаниями. Интересно, что курс фьючерсных контрактов рос при начальном повышении курса доллара, но заметно не отреагировал собственно на черный вторник. Тем самым, уже простое изучение графиков временных рядов дает нам достаточно много предварительной информации.

     Постановка задачи. Очевидно, что упомянутые процессы развиваются в некоторой информационной среде, обладающей собственной инерционностью и упругостью, что определено существующими организационной и инфраструктурой, менталитетом участников и заинтересованных лиц и кучей других факторов, не поддающихся непосредственному учету. Эти динамические свойства налагают определенные ограничения на передачу взаимодействия от одного процесса к другому, на периодичность колебаний и крутизну фронтов роста и спада.

     Варианты анализа. Прямое прогнозирование курса доллара мало что может дать, сверх моделирования общей возрастающей тенденции. Предсказание резких изменений типа черного вторника (см. разд. 14.4) возможно только в непосредственной близости от такого рода событий и при наличии сильно развитой интуиции.
     Если же попробовать прогнозировать фьючерсные котировки, то даже применение таких изощренных методов как модели Бокса–Дженкинса, вплоть до 12–го авторегрессионного порядка, дает нам лишь общее представление о динамике средней тенденции на очень короткое будущее, а различные конкретные генерации прогнозов существенно отличаются друг от друга. Возможно, что более надежные результаты дало бы моделирование и прогнозирование изменений курса (первая производная) или скорости этих изменений (вторая производная, характеризующая инерционность процессов).
     Сначала попробуем построить интервальную автокорреляционную функцию временного ряда fut, выбрав в качестве сдвигаемого фрагмента 10 первых измерений, содержащих резкий выброс. Поэтому автокорреляционную функцию такого ряда можно рассматривать как переходную характеристику реакции системы на начальное возмущение.

Р е з у л ь т а т ы:
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ.  Файл: spec.std
 Переменные: fut,fut  Критич.значение=0.621


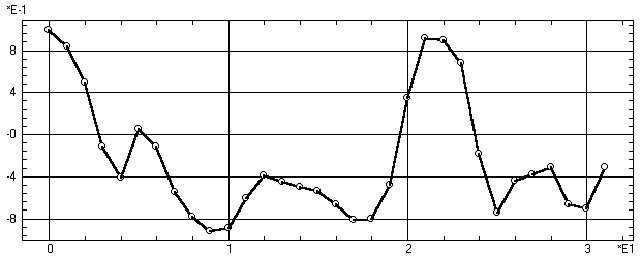
Рис. 5. Автокорреляционная функция фьючерсных котировок доллара. По горизонтальной оси — величина лага

     Обсуждение. Как следует из рис. 5 автокорреляционная функция на первых 18 лагах достаточно монотонно уменьшается в область отрицательных значений, т. е. динамика временного ряда становится все более обратной по сравнению с начальным участком.
     Однако на 18—20 лаге наступает резкий, но короткий переход к практически 100%–ной коррелированности с начальным участком. Такая задержка и характер отложенной реакции может служить важным показателем свойств исследуемой среды.

     Продолжение анализа. Построим теперь интервальную кросскорреляционную функцию, отражающую влияние процесса fut на процесс dol.


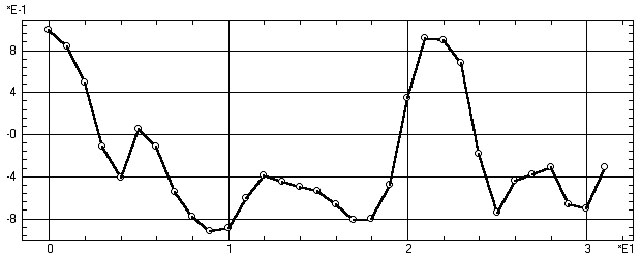
Рис. 6. Кросскорреляционная функция фьючерсных котировок доллара на курс доллара

     Обсуждение. Полученная кросскорреляционная функция (рис. 6) достаточно монотонна, кроме начального отрицательного выброса, что подтверждает вполне очевидное заключение: фьючерсные котировки доллара мало влияют на сам курс доллара.

     Продолжение анализа. Построим теперь интервальную кросскорреляционную функцию, отражающую влияние процесса dol на процесс fut. Для сравнения вычислим также и классическую корреляционную функцию, а для большей наглядности совместим их числовые выдачи и графики.

Р е з у л ь т а т ы:
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ.  Файл: spec.std  Переменные: dol, fut
  Сдвиг  Интерв.корр. Класс.корр. Крит.значение
Критич.значение=0.621
        0      0.483    –0.0036        0.304
        1       0.29    –0.185         0.308
        2      0.296    –0.237         0.312
        3     0.0362    –0.305         0.316
        4    0.00264    –0.289         0.321
        5      0.489    –0.159         0.325
        6    –0.0451    –0.226         0.33
        7     –0.547    –0.3           0.335
        8     –0.572    –0.269         0.34
        9     –0.527    –0.216         0.345
       10     –0.487    –0.144         0.351
       11     –0.212    –0.0355        0.357
       12   0.000573     0.0329        0.363
       13   –0.00285     0.0442        0.369
       14     –0.079     0.0304        0.376
       15      –0.39    –0.0492        0.383
  . . . . . . . .


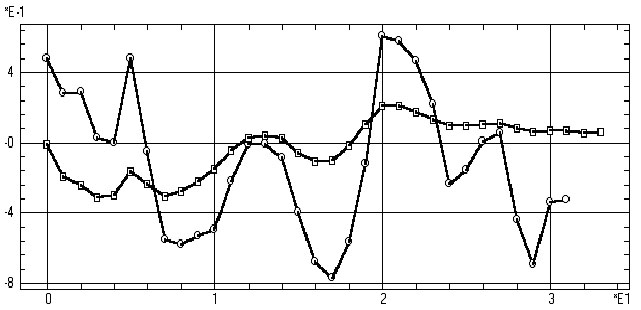
Рис. 7. Кросскорреляционная функция курса доллара на его фьючерсные котировки
(квадраты — классическая корреляция, круги — интервальная корреляция)

     Обсуждение. Интервальная корреляционная функция (рис. 7) достоверно воспроизводит отложенную на 18–20 лагов резкую положительную реакцию фьючерсных котировок на начальный скачок курса доллара, отмеченную еще в автокорреляционной функции. Что же касается классической корреляционной функции, то по ее графику нельзя сделать никаких существенных выводов, поскольку все ее значения не отличны от нуля, а колебания незначительны.
     Полученные статистические результаты дают нам несравненно более значимые материалы для выработки финансовой стратегии, чем моделирование и прогнозирование, предупреждая о том, что следует обращать особое внимание на динамику процессов спустя 18–20 дней после очередного возмущения. Эти же материалы дают пищу специалистам для размышлений о физических свойствах среды, передающей взаимодействие процессов с такими большими задержками.

     Что дальше? Здесь мы рассмотрели экстремальный случай реакции системы на резкое начальное возмущение. Дальнейший анализ может развиваться в направлении исследования взаимодействия процессов в обычных условиях, не содержащих резких колебаний. Оставляем эту задачу в качестве учебной читателям.