Краткая история квантовой
механики
Квантовую механику не понимает
никто
Ричард Фейнман
Если же вы никогда не чувствуете
себя ошеломленным, когда размышляете о квантовой механике, значит, вы далеки
от ее понимания
Нильс Бор
Если вы не можете объяснить
результат на простом, не отягощенном специальными терминами языке, значит,
вы его сами не понимаете
Эрнест Резерфорд
Первая "памятка" посвящена
истории постепенного и долгого проникновения в глубинный смысл постоянной
Планка, которая является краеугольным камнем как собственно квантовой механики,
так и базиса нашего Мироздания.
.
Великие участники:

Ньютон
|

Максвелл
|

Планк
|

Эйнштейн
|

Бор
|

де Бройль
|

Гейзенберг
|

Шредингер
|

Дирак
|

Фейнман
|

Вайнберг
|
Истоки.
В конце XIX века в физике был обнаружен парадокс при расчете общей энергии
электромагнитного излучения в замкнутой полости (абсолютно черное тело).
Из теории Максвелла (1890) следовало, что длина волны излучения должна
быть кратной расстоянию между стенками полости (там должно помещаться целое
число волн). Из термодинамики следует, что в состоянии равновесия каждая
волна независимо от частоты будет нести одно и то же количество энергии
Е,
определяемой температурой полости. Но поскольку ряд допустимых частот бесконечен,
то и общая энергия излучения получается бесконечной.
Первый
шаг. В 1900 Макс Планк предположил, что энергия электромагнитной
волны может изменяться только целыми порциями, а минимальная энергия, которую
может нести волна, пропорциональна ее частоте (Нобелевская премия 1918).
Поэтому в замкнутой полости число частот электромагнитного излучения не
бесконечно, а ограничено: не может существовать волн, минимальная энергия
которых превышает Е. Из экспериментальных измерений энергии замкнутой
полости Планк рассчитал коэффициент пропорциональности между минимальной
энергией волны Е и ее частотой n: Е=hn
(как это кажется просто!), который получил название постоянная Планка
(h=1,05*10-27 г*см2/с).
Никто не понимал, почему энергия волн должна быть дискретной, за исключением
того, что это работает. И проникновение в смысл постоянной Планка длилось
многие десятилетия.
1-е
объяснение. В 1905 Эйнштейн нашел этому объяснение, за
которое в 1921 получил Нобелевскую премию. Он изучал фотоэффект, открытый
в 1887 немецким физиком Генрихом Герцем: когда свет падает на некоторые
металлы, то они испускают электроны. Казалось, что при увеличении интенсивности
(яркости) света скорость электронов должна возрастать, поскольку свет будет
нести больше энергии. Однако скорость оставалась постоянной, но увеличивалось
количество электронов, скорость же увеличивалась только при увеличении
частоты света. При уменьшении же частоты наступал момент, когда электроны
перестают вылетать (их скорость вылета падает ниже нуля).
Эйнштейн решил распространить
планковскую дискретную модель энергии волны на свет. Он предположил, что
свет представляет собой поток микроскопических частиц (названных в 1929
химиком Гильбертом Льюисом фотонами), причем энергия каждого фотона пропорциональна
частоте света. Тогда, чтобы вырваться с поверхности металла, электроны
должны испытать соударение с фотонами, обладающими определенным минимумом
энергии. Поэтому, если частота света будет слишком мала, то фотоны не будут
нести энергию, достаточную для выбивания электронов из металла. Таким образом
Эйнштейн показал, что гипотеза Планка о дискретности энергии отражает фундаментальное
свойство электромагнитных волн: они состоят из частиц — фотонов, которые
представляют собой маленькие порции или кванты света. Тем самым
дискретность энергии волн определяется тем, что они состоят из дискретных
объектов. В 1923 американский физик Артур Комптон подтвердил корпускулярную
природу света в экспериментах по рассеянию рентгеновских фотонов на свободных
электронах. Его расчеты показали, что коэффициент пропорциональности между
энергией и длиной волны фотона тоже равен постоянной Планка, которую он
вычислил с точностью до 1%.
Принципиальный эксперимент Юнга. Рассматривать свет состоящим
из потока частиц, предложил еще Ньютон. Ему оппонировал голландский физик
Христиан Гюйгенс, утверждавший, что свет — это волна. В начале XIX в эксперименты
английского физика Томаса Юнга (по интерференции света, пропускаемого через
две щели, рис.1) показали, что Ньютон ошибался. Фейнман любил говорить,
что вся квантовая механика может быть выведена из одного этого эксперимента.
Можно было бы привести аналогию с морем, состоящим из отдельных молекул
воды, которые совместным движением могут создавать волны. Но микромир устроен
более тонко. Даже если через щели будем пропускать одиночные фотоны с большими
временными интервалами, интерференционная картина за щелями сохранится.
Как будто фотоны могут друг с другом сговориться двигаться так, чтобы за
экраном чаще попадать в светлые полосы, чем в темные. Фотоэффект и опыт
с двумя щелями показали, что фотоны обладают и волновыми и корпускулярными
свойствами одновременно.
.

Рис.1. Круговые волны на воде,
идущие от каждой щели, накладываются одна на другую: это приводит
к тому, что в одних местах результирующая волна будет усиливаться, а в
других ослабляться
|
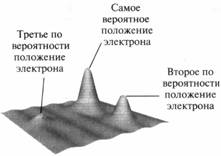
Рис.2. Волна, ассоциированная с электроном, имеет
наибольшую амплитуду там, где обнаружение электрона наиболее вероятно,
амплитуда волны убывает по мере уменьшения вероятности обнаружения электрона
|
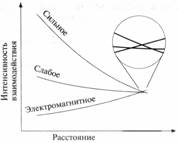
Рис. 3. Уточнение расчета интенсивностей взаимодействий
показало, что без суперсимметрии они очень близки, но не совпадают
|
.
Материя тоже
волновая. В 1923 молодой французский аристократ, князь
Луи де Бройль объединил две гипотезы, что принесло ему Нобелевскую премию
1929: эйнштейновское E=mc2 связывает массу с энергией,
но Планк и Эйнштейн связали энергию с частотой волн. Объединяя эти два
предположения, можно прийти к выводу, что масса должна иметь и волновое
воплощение. В середине 20-х Клинтон Девиссон и Лестер Джермер, физики-экспериментаторы
из лаборатории телефонной компании Белл, подтвердили волновые интерференционные
свойства электронов при их рассеянии на атомах никеля. Расчеты показали,
что длина волны электрона обратно пропорциональна его энергии с коэффициентом
пропорциональности, равным постоянной Планка. Это было уже третье непонятное
совпадение, и отсюда постоянная Планка стала приобретать универсальный
и фундаментальный характер.
Волновые
функции. Встал вопрос: волны
чего? Австрийский физик Эрвин Шредингер предположил, что эти волны представляют
собой размазанные по пространству электроны. В 1926 немецкий физик Макс
Борн внес важное уточнение (усиленное главой "копенгагенской школы" Нильсом
Бором с коллегами), что эти волны должны интерпретироваться как волны вероятности
(рис.2): вероятность обнаружить электрон в заданной точке равна квадрату
амплитуды его волны в этой точке (Нобелевская премия 1954). Вскоре Шредингер
предложил уравнение для расчета этих волн вероятности или волновых функций,
а Поль Дирак расширил его, записав в релятивисткой форме (оба получили
Нобелевскую премию 1933), что позволило предсказать магнитные свойства
электрона и доказать наличие спина у элементарных частиц. Дальнейшее обобщение
волнового уравнения было вскоре сделано Клейном и Гордоном. Собственные
решения волнового уравнения Шредингера можно было истолковать как систему
стоячих электронных волн в окрестности ядра, определенным образом соответствующую
системе стационарных состояний.
Альтернатива
Гейзенберга. Немецкий физик Вернер Гейзенберг с 1925
(совместно с работами Макса Борна и Паскуаля Йордана) начал развивать другой
формализм описания микромира, названный им матричной механикой,
которая описывала квантовые явления с помощью таблиц наблюдаемых величин.
Эти таблицы представляют собой определенным образом упорядоченные математические
множества, называемые матрицами, над которыми по давно известным правилам
можно производить различные математические операции. Тем самым микрореальность
допускала и другие математические описания и находила прямое отражение
в математике. Метод квантовой механики, оперирующий прямо с матрицами и
не имеющий дела с промежуточными величинами — волновыми функциями, более
компактен и часто быстрее приводит к желаемым результатам. Метод же волновой
механики лучше удовлетворяет интуиции физиков и лучше согласуется с образом
их мыслей. Однако интерпретация этой квантовой механики (с формальными
операциями над матрицами), исходя из обычных кинематических и механических
представлений, оказалась невозможной. Такие понятия как "положение", "скорость",
"траектория" и связанные с ними представления о непрерывном течении событий
и о причинности словно повисли в воздухе. Гейзенберг особенно настаивал
на отказе от каких-либо простых наглядных представлений или моделей в пользу
только таких свойств, которые могли быть определены из эксперимента, и
эта концепция была развита копенгагенской школой. Шредингер же, наряду
с Эйнштейном и де Бройлем, был среди противников копенгагенской интерпретации
квантовой механики, поскольку его отталкивало отсутствие в ней детерминизма.
Итак, существовала совокупность
экспериментов. Существовала логически непротиворечивая, математически изящная
теория (даже две, Шредингер показал, что волновая механика и матричная
механика математически эквивалентны), корректно описывающая эксперименты.
Но — отсутствовали понятия, с помощью которых можно было бы описать
объект
исследования. Материальная точка, траектория, волна — это не "образы".
В системе классической физики это полноценные понятия со своей логикой
и онтологией, позволявшие говорить о том, что собственно мы наблюдаем и
описываем. В новой механике все эти объекты превращались из "вещей", поведение
которых описывается в теории, в "язык" описания неведомых "объектов". Было
неясно, что же можно поставить на их место. Тем не менее, адекватность
абстрактных математических конструкций и физической реальности сама по
себе вызывает крайне удивление и заставляет глубоко задуматься. В этом
мы еще более убедимся при рассмотрении теории струн.
Альтарнатива
Фейнмана. Ричард Фейнман в 50-х предложил новый взгляд
на квантовую проблему. Он усомнился в классической картине, что каждый
электрон проходит только через одну щель. Фейнман предположил, что электрон
не только проходит через обе щели, но и одновременно перемещается (рыщет)
по всем возможным траекториям от источника до экрана (включая и путь к
туманности Андромеды и обратно). Каждому из этих путей можно поставить
в соответствие некоторое число, и их сумма даст искомую вероятность. Этот
подход получил название суммирование по путям. Фейнман говорил:
"Квантовая механика дает совершенно абсурдное с точки здравого смысла описание
Природы. Но оно полностью соответствует эксперименту. Поэтому следует принять
Природу такой, какой Она есть, — абсурдной". В отличие от матричной механики
этот принцип получил свое развитие и применение во многих последующих теориях.
Смысл постоянной
Планка. Электрону должно быть все равно, существует или
нет вторая щель, но каким-то образом он чувствует ее наличие или отсутствие.
Можно попытаться определить, через какие щели проходят электроны, бомбардируя
их фотонами. Однако положение электрона можно определить только с точностью
до длины волны фотона. Уменьшая длину волны, мы увеличиваем точность определения
положения, но вносим все большую неопределенность в скорость электрона
(благодаря все большей энергии фотонов). Так или иначе, интерференционная
картина исчезнет, т.е. своим знанием о положении электрона мы уничтожаем
его волновые свойства!
Все это в 1927 побудило
Гейзенберга сформулировать соотношение неопределенностей: точность
определения положения Dx обратно пропорциональна
точности определения скорости (импульса Dр),
а коэффициент пропорциональности равен постоянной Планка: DхDр~h.
Исследования 90-х показали (Джон Белл, Алан Аспект и др.), что это соотношение
носит фундаментальный характер: если поместить электрон в коробку и начать
сближать ее стенки, то он начнет метаться с все большей и менее определенной
скоростью. Соотношение неопределенности лежит в основе еще одного потрясающего
явления — квантового туннелирования: низкоэнергетические частицы
могут "просачиваться" через непреодолимый высокоэнергетический барьер (если
стрелять пулями по стальной стене, то небольшая часть пуль проскочить через
стену).
Гейзенберг показал также
обратно пропорциональную связь между точностью измерения энергии частиц
DE
и временем ее измерения Dt:
DEDt~h.
В дальнейшем это привело к концепции виртуальных частиц: на очень
короткое время можно "занять" (а затем "вернуть") очень большую энергию
с порождением кратковременных частиц. Невероятная энергетическая активность
в микромире все более возрастает по мере уменьшения масштабов расстояния
и времени. На ультрамикроскопических масштабах (порядка планковской длины
1,616*10-33 см, если атом
увеличить до размера Вселенной, то планковская длина будет равной высоте
среднего дерева) всплески энергии столь велики, что вследствие общей
теории относительности рушится привычная гладкая топология пространства-времени
(флюктуации массы, а следовательно — и тяготения становятся огромными)
— в ней возникают ручки, дырки и т.п. — хаос квантовой пены (по
выражению Джона Уилера). Но поскольку заем и возврат в среднем компенсируют
друг друга, пустое макроскопическое пространство продолжает выглядеть тихим
и спокойным.
Объединение
с релятивиизмом. Окончательное расширение уравнений Шредингера
на релятивистские ситуации было достигнуто только в послевоенное время
с разработкой квантовой электродинамики (Юлиан Швингер, Фриман Дайсон,
Син-Итиро Томонага, Фейман и др.), в последствии получившей название
релятивистская
квантовая теория поля. Иллюстрацию ее точности можно найти в работах
Тойхиро Киношиты из Корнельского университета, который 30 лет с помощью
мощнейших суперкомпьютеров неутомимо рассчитывал тонкие свойства электрона.
Его результаты, занимающие тысячи страниц, экспериментально подтвердились
с точностью в одну миллиардную.
Объединение
2-х взаимодействий. Четыре фундаментальных взаимодействия
колоссально различаются по интенсивности. Интенсивность электромагнитного
взаимодействия не превышает одного процента от интенсивности сильного взаимодействия.
Слабое взаимодействие примерно в тысячу раз слабее электромагнитного, а
интенсивность гравитационного взаимодействия слабее еще в 1035
раз. К 1968 Шелдон Гелшоу, Абдус Салам и Стивен Вайнберг разработали электрослабую
теорию, объединяющую слабое и электромагнитное взаимодействия, за что
были удостоены Нобелевской премии 1979.
Объединение
3-х взаимодействий. Эти успехи подвигли физиков в 60—70-х
гг. разработать квантовую хромодинамику, объединяющую электромагнитное,
слабое и сильное взаимодействия (так называемая стандартная модель).
Гэлшоу и Говард Джоджи из Гарвардского университета выяснили, что хотя
слабое и сильное взаимодействия работают только на субатомных масштабах,
а электрическое — вплоть до космических, но спустя долю секунды после Большого
взрыва они были слиты одно с другим. Вследствие дальнейшего снижения температуры
произошло нарушение симметрии (фазовый переход) и эти взаимодействия разделились
(выкристаллизовались). Выводы теории согласуются с экспериментами вплоть
до предельно достижимых на настоящее время масштабов 10-18 м.
Еще в 1974 Джорджи, Хелен
Куин и Вайнберг в Гарварде осознали, что когда мы исследуем электрическое
поле электрона, то измеряем его через "туман" виртуальных электрон-позитронных
пар, непрерывно рождающихся и аннигилирующих в окружающей его области пространства.
Это маскирует его поле, как обычный туман ослабляет свет маяка. При проникновении
же сквозь этот туман электрическое поле электрона будет возрастать. В 1973
Гросс и Френк из Принстона и Дэвид Политцер из Гарварда исследовали аналогичный
вопрос относительно слабого и сильного взаимодействий. Оказалось, что здесь
имеет место обратный эффект — уменьшение их интенсивностей при приближении
сквозь "туман". На этой основе Джорджи, Куинн и Вайнберг показали, что
если аккуратно учесть влияние всех квантовых флюктуаций, то интенсивности
трех негравитационных взаимодействий начнут сближаться, и на расстоянии
10-29 см они окажутся почти одинаковыми. В 1991 Уго Амальди
из ЦЕРНа, Вим де Боер и Герман Фюрстенау из университета Карсруэ в Германии
пересчитали результаты предшественников и показали, что небольшая несогласованность
исчезает при включении в теорию суперсимметрии, поскольку новые
частицы-суперпартнеры дают дополнительные квантовые флюктуации, которые
делают интенсивности на туманом в точности равными (рис.3).
Суперсимметрия.
В 1971 в теории струн было показано, что если рассматривать спин с математической
точки
зрения, то возможна еще одна дополнительная симметрия законов природы,
которая получила название суперсимметрии. В этом случае все частицы должны
наблюдаться парами со спином на 1/2 меньше. Но ни одна из известных частиц
не может быть сеперпартнером для другой. Приблизительный прогноз показал,
что суперпартнеры должны быть более чем в 1000 раз тяжелее протона. Такая
энергия не достижима на современных ускорителях. Суперсимметрия привлекательна
и с чисто эстетических соображений, поскольку трудно примириться с тем,
что природа реализовала все математически возможные виды симметрии, кроме
одной. Кроме того, даже в рамках стандартной модели суперсимметрия позволяет
разрешить многие технические трудности, связанные с квантовыми эффектами,
поскольку суперпартнеры вносят корректирующий вклад в квантовый хаос.
Великое
объединение. Однако объединение с четвертым взаимодействием
— гравитационным в рамках стандартной модели не было достигнуто, поскольку
совместное применение уравнений квантовой механики и общей теории относительности
в планковских масштабах приводит к бесконечностям (для модели точечных
частиц). Ликвидация этих бесконечностей была достигнута только в теории
суперструн.















