ШРИ ЯНТРА - ТАЙНЫ ГЕОМЕТРИИ
воспроизведено по публикации:
Indian Journal of History of Science, 19 (3): p:279—292 (1984)
SRIYANTRA AND ITS MATHEMATICAL PROPERTIES
ALEXEY PAVLOVICH KULAICHEV
Biology Faculty of Moscow University, Moscow, USSR
(Received 29 July 1983)

Рис. 1. Шри Янтра в одной из традиционных палитр

        Метафизика. Имеется два способа рассмотрения Шри Янтры в процессе медитации: изнутри-вовне и извне-вовнутрь, то есть из центральной точки бинду (bindu) к бхупуре («квадрат защиты») через концентрические цепи малых треугольников, лепестков лотоса и линий квадрата защиты, или же в обратном направлении. Эти два метода используются в двух тантристких ритуалах правого и левого направлений, соответственно. Направление медитации изнутри-вовне ассоциируются с эволюционным развитием Вселенной от исходного точечного, вневременного и внепространственного состояния (имманентное единство Шивы и Шакти: высшего сознания и высшей энергии, мужского и женского основополагающих принципов) к феноменальному проявлению и к все большей и большей дифференциации и усложнению форм материи. Противоположенное направление рассмотрения Шри Янтры ассоциируется с обратным процессом деструкции Вселенной, заканчивающимся в точечном недифференцированном состоянии.
        Психофизика. В процессе медитации адепт (sadhaka) осуществляет проекцию эволюционно-инволюционного процесса на свое тело, целью которого является пробуждение энергии Шакти, именуемой Кундалини, которая спит в основании позвоночника (в так называемой Муладхара-чакра, ассоциируемой с бхупурой Шри Янтры). Далее, зрительно трассируя Шри Янтру к центру, адепт старается направить эту энергию вверх по позвоночному столбу до слияния с аспектом Шивы, располагающимся в головной чакре (Сахасхара-чакра, ассоциируемая с бинду Шри Янтры). Таким образом как бы проходится путь, обратный развитию вселенной. Поэтому, согласно тантристкой доктрине, в конечной точке этого процесса достигается неописуемое расширение восприятия с полным знанием основ мироздания. Выполняя обратную процедуру, адепт возвращается к своему обычному чувственному (телесному) восприятию.

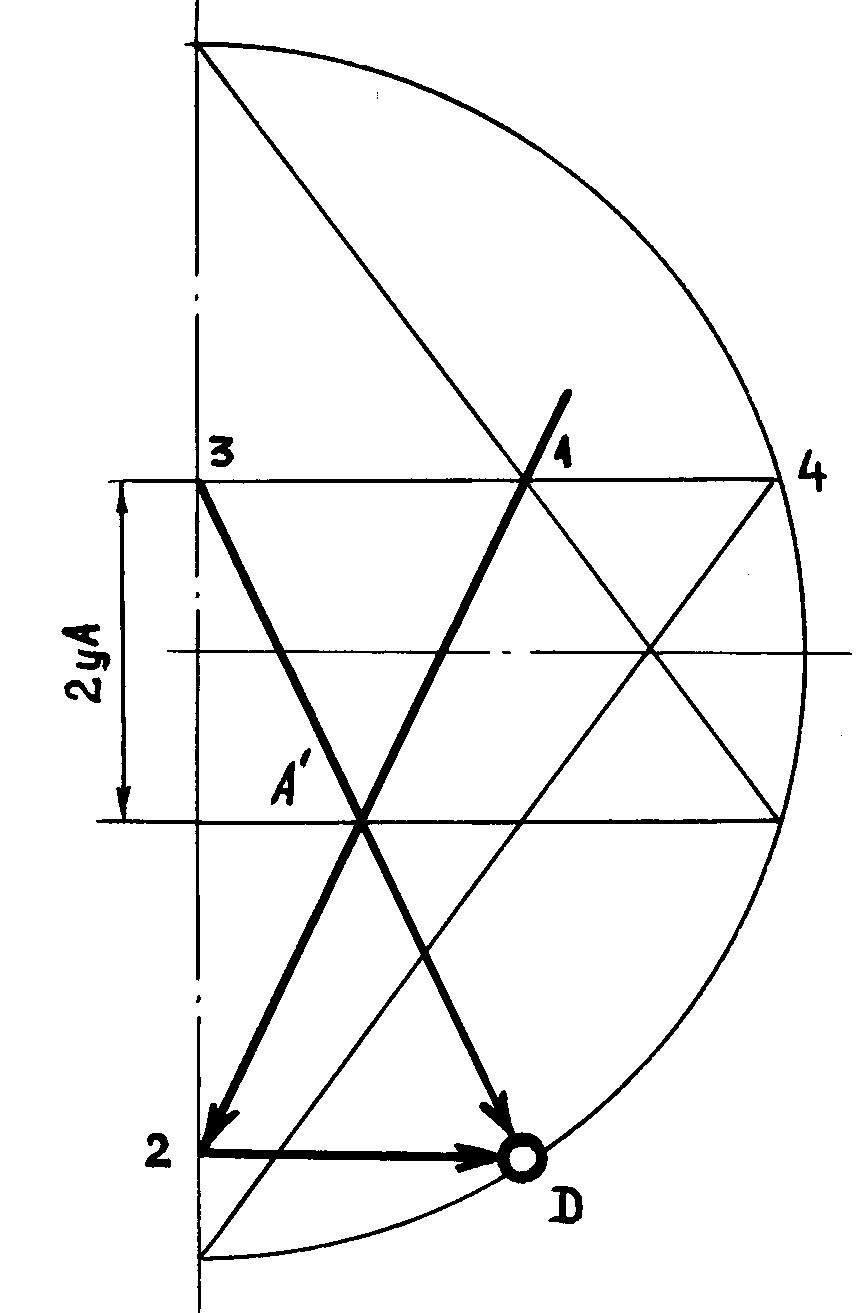
а) компонент 1: Delta-yD = f(xA’)

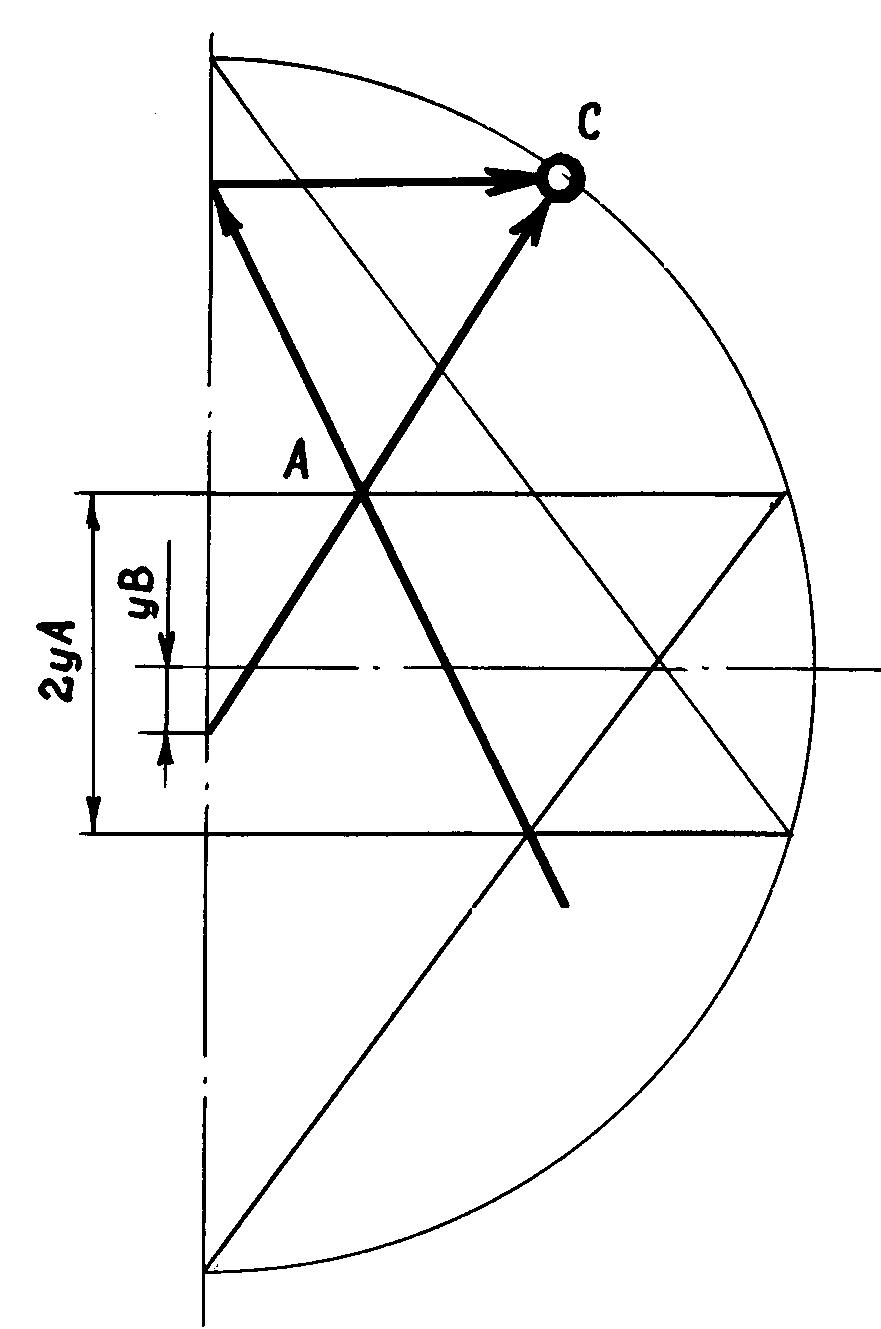
б) компонент 2: Delta-yC = f(xA)

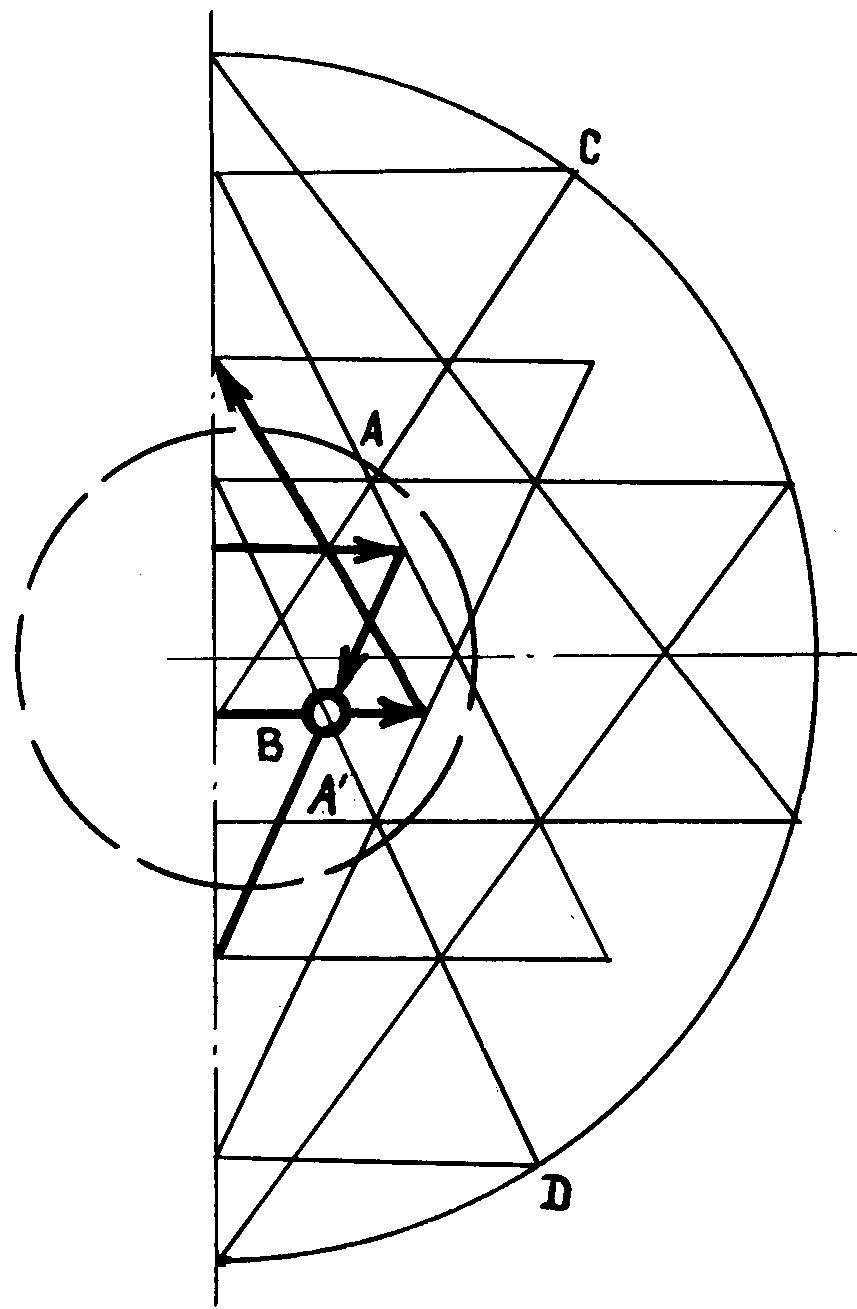
в) компонент 3: Delta-xB = f(yB)

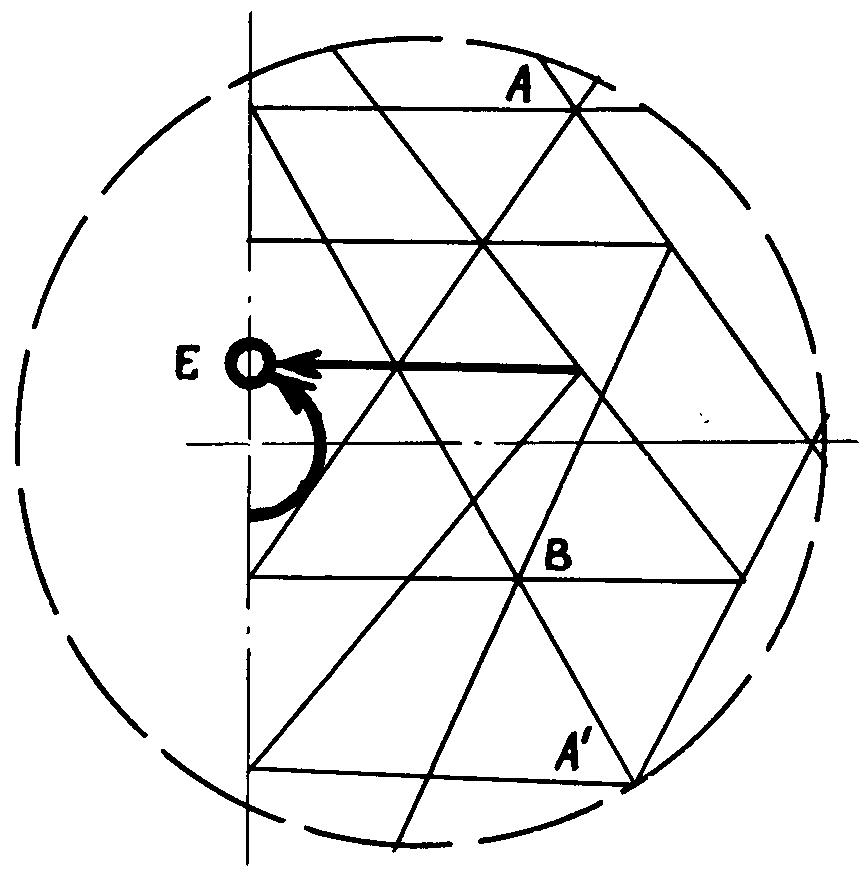
г) компонент 4: Delta-yE = f(yA)

        Затем произвольно выберем точку A’ на основании вверх направленного треугольника (фактически — выберем значение xA’) и проведем прямую через точки 1 и A’ до пересечения с вертикальной осью круга, а затем начертим горизонталь через точку 2 до пересечения с окружностью, получая точку D. Теперь, имея три точки 3, A', D, мы должны провести линию через точки 3, A' до пересечения с окружностью и хотели бы, чтобы это пересечение совпало с точкой D. Однако чтобы достичь этого, требуется выполнить целую последовательность перестроений фигуры (итераций или последовательных приближений — в математической терминологии) с некоторым перемещением точки A’ и с оценкой на каждом шаге этого процесса степени погрешности несовпадения завершающей точки пересечения с точкой D.
        Конструкция и построение компонента 2 (рис. 2б) почти симметричны компоненту 1 и независимы от него, причем априорно выбираемое значение yB потом надо будет корректировать при построении компонента 3. Когда компоненты 1 и 2 построены с удовлетворительной точностью совмещения точек пересечения, мы имеем все линии, необходимые для рисования компонента 3 (рис. 2в). В этом процессе обнаружится несоответствие точки пересечения завершающей линии с уже имеющейся точкой B, для уменьшения которого придется изменить yB и, следовательно, — снова итерационно перестроить компонент 2. При построении компонента 4 (рис. 2г) возникнет несоответствие основания внутреннего треугольника и вписанной в него окружности, которое можно пытаться нивелировать только изменением значения yA с повторением всех итерационных перестроений трех предшествующих компонентов.
        Итерационные построения. Тем самым, взаимодействие между четырьмя итерационными процедурами построения структурных компонентов включает два уровня вложенности (рис. 3), а именно: на каждом шаге приближения третьего компонента требуется повторение полного цикла итераций по компоненту 2, а на каждом шаге приближения компонента 4 необходимо выполнить три вложенных итерационных процедуры. Если мы обозначим символами a, b, c, d число итерационных шагов, необходимых для построения компонентов 1-4 с некоторой заданной точностью, то общее число перерисовок N звезды Шри Янтры можно выразить формулой:

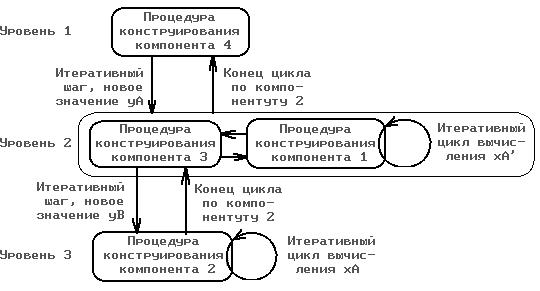
Рис.3. Схема итерационных построений звезды Шри Янтры

        Вышерассмотренная вложенная четырехступенчатая процедура представляется единственно возможной техникой, если мы желаем увеличить точность воспроизведения конструкции звезды Шри Янтры. Однако для простого копирования звезды с имеющегося образца в рамках его точности достаточно знания значений четырех параметров, которые определяют геометрию четырех структурных компонентов (в рассмотренном случае это: yA, yB, xA, xA’, однако из практических соображений удобнее выбрать уровни четырех горизонталей, например: yA, yB, yC, yD).
        Аналитическое описание. Обратимся теперь к проблеме аналитического описания звезды Шри Янтры. Пользуясь простыми уравнениями прямой и окружности для каждой пары линий в звезде, мы можем в аналитическом виде определить координаты точки их пересечения. Имея полный комплект таких уравнений, посредством последовательной подстановки (суперпозиции) координат точек пересечения из одного уравнения в другое, мы можем попытаться вывести результирующие уравнения, описывающие каждый из четырех структурных компонентов. Так, в простейшем случае компонента 1 мы имеем (см. рис. 2а) следующую систему уравнений для координат точек пересечения (не уменьшая общности, для простоты примем, что радиус внешней окружности = 1):

        Корни. Из геометрической природы системы 4 следует, что она обязана иметь не менее одного действительного решения (корня) относительно переменных yA, xA, xA', yB, которое может быть вычислено с заданной точностью посредством некоторого итерационного численного метода (например, метода наикратчайшего спуска). Вычисленное нами решение имеет следующие значения:

        Общее решение. Но, с другой стороны, известно, что любой полином n-ой степени имеет ровно n решений (корней), из которых некоторые могут быть действительными, а некоторые — мнимыми. Применительно к Шри Янтре мнимые корни не имеют геометрического смысла, и они нас не интересуют. Однако система 4 может иметь и другие действительные решения, кроме найденного комплекта корней 5. Поэтому правомерен и логичен вопрос: есть ли еще другие подобные решения и, если — да, то сколько их? Иными словами, сколько существует различных расположений девяти пересекающихся треугольников в Шри Янтре?
        Современная математическая теория (высшая алгебра) не дает прямого ответа на этот вопрос. Применение же итерационных численных методов для нахождения других корней требует предварительного знания границ их локализации.
        Упрощенно пояснить это можно следующим образом. Геометрически систему уравнений 4 можно представить как некую сложную суперповерхность в пространстве четырех измерений (независимых переменных). Задачу поиска корней системы 4 можно интерпретировать, как нахождение всех минимумов такой поверхности. Однако в связи с высокой степенью системы уравнений 4 большинство таких минимумов (если они вообще существуют) представляют собой резкие провалы крайне малого диаметра, поэтому случайно попасть в такой провал итерационным алгоритмом практически невозможно, если только не запускать работу алгоритма с точки, расположенной непосредственно на отвесном "склоне" каждого такого провала.
        Так вот, рассматриваемая задача предварительной локализации корней математически разрешима только для полинома от одной переменной. Теоретически систему 4 посредством последовательного исключения переменных (подстановка одного уравнения в следующее) можно преобразовать в полином не более чем 12544 степени от одной переменной, после чего локализовать корни и затем уже - вычислить их значения численным методом. Однако оказывается, что для этого уже на первом простейшем шаге преобразований (из трех необходимых) следует выполнить (по предварительной оценке) не менее 1011 элементарных операций, причем объем вычислений на каждом последующем шаге, по крайней мере, в 100 раз больше предыдущего. Более того, исследование полученного результирующего уравнения требует оперирования с числами, представленными с точностью не менее четырех тысяч десятичных значащих цифр. Отсюда ясно, что такая задача далеко превосходит возможности самых мощнейших земных суперкомпьютеров. Это, мягко говоря, немного озадачивает...
        Вопросы. Такой необнадеживающий вывод порождает целую серию вопросов, например: какие инструментальные средства и знания использовались для воспроизведения звезды Шри Янтры на протяжении тысячелетий? или: Как вообще могла возникнуть идея о том, что девять треугольников способны пересекаться в таком многоугольнике с точным совпадением многочисленных точек пересечения? и многие другие. Для предварительного ответа на подобные вопросы, прежде всего, требуется исследование распространенности во времени и по численности различных образцов Шри Янтры. К сожалению, имеющийся в доступности материал для такого исследования более чем скуден.

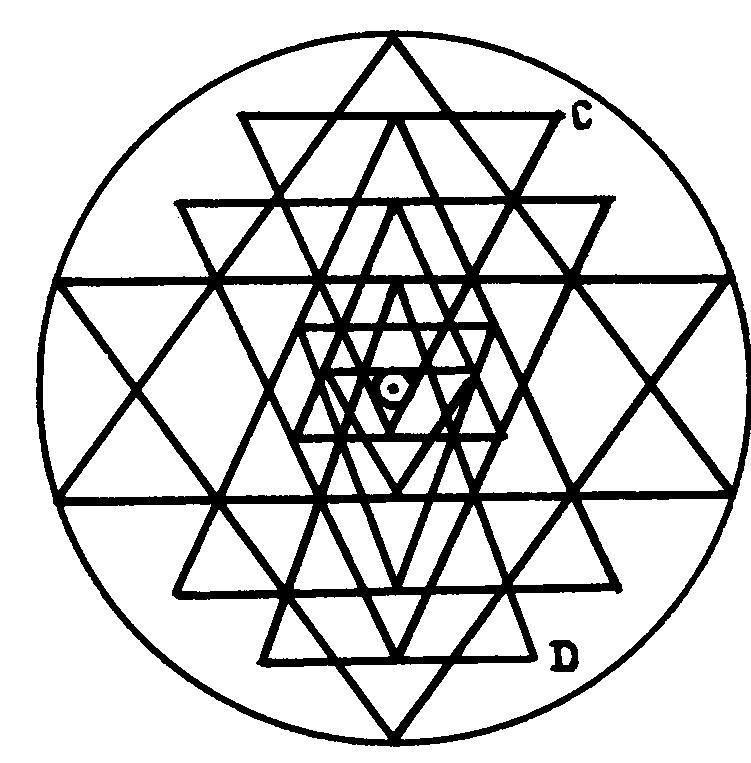
а) тип I

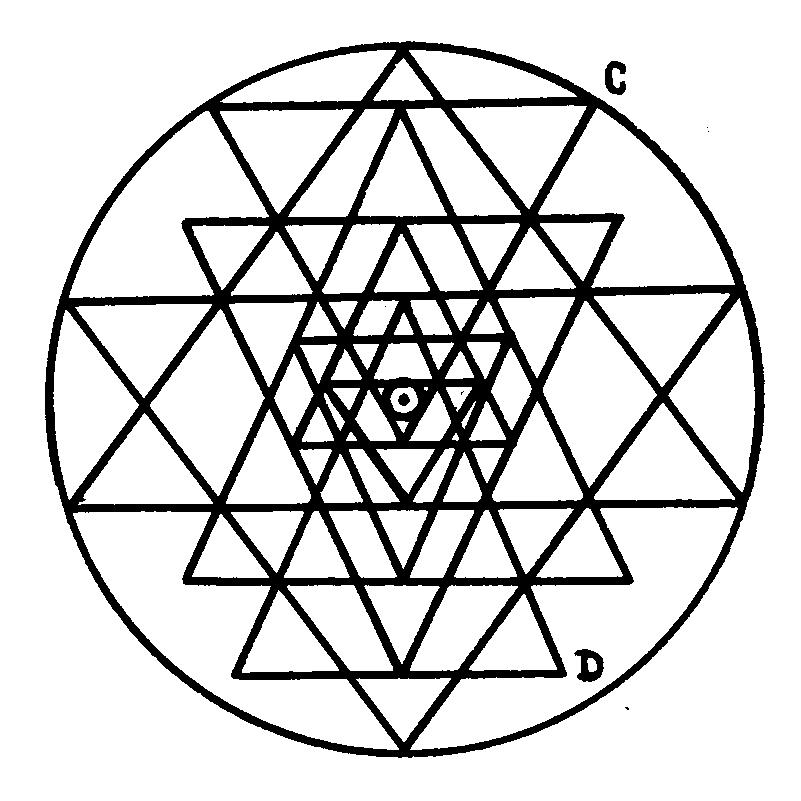
б) тип II

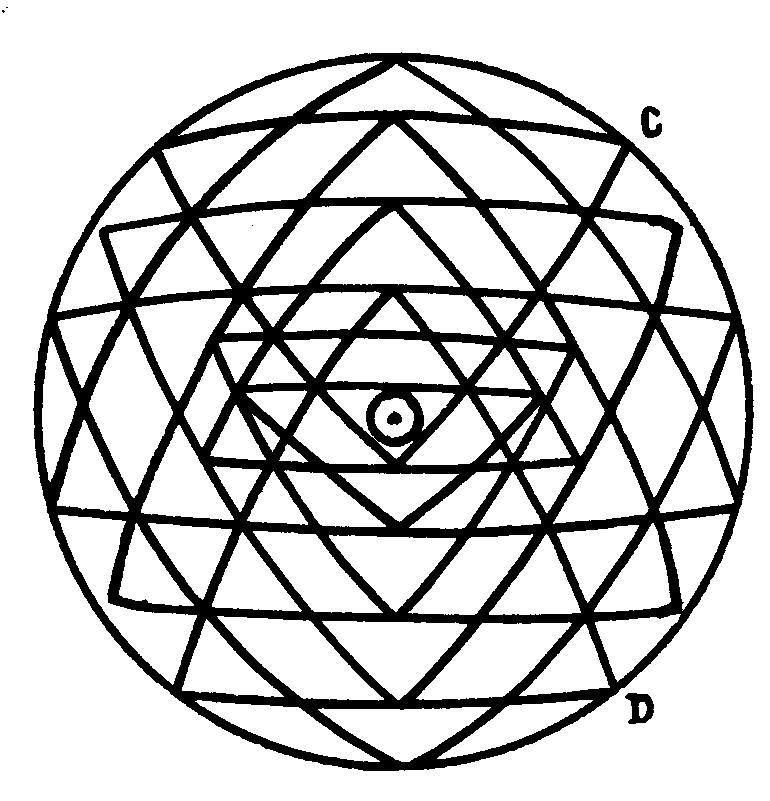
в) тип III

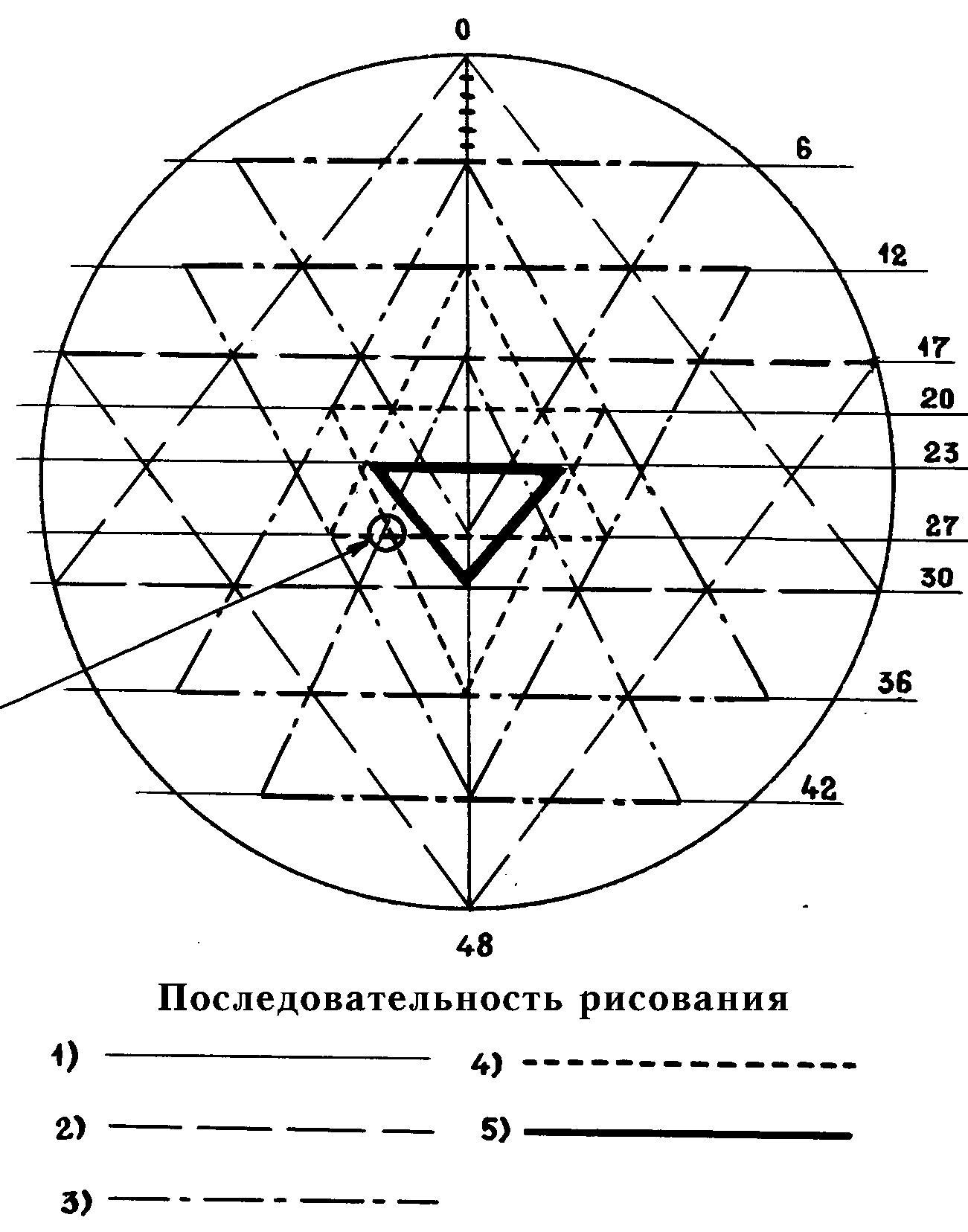
Рис. 5. Традиционный метод построения звезды Шри Янтры типа I в порядке деструкции (samhara-krama). Стрелкой указано явное несовпадение точек пересечения.

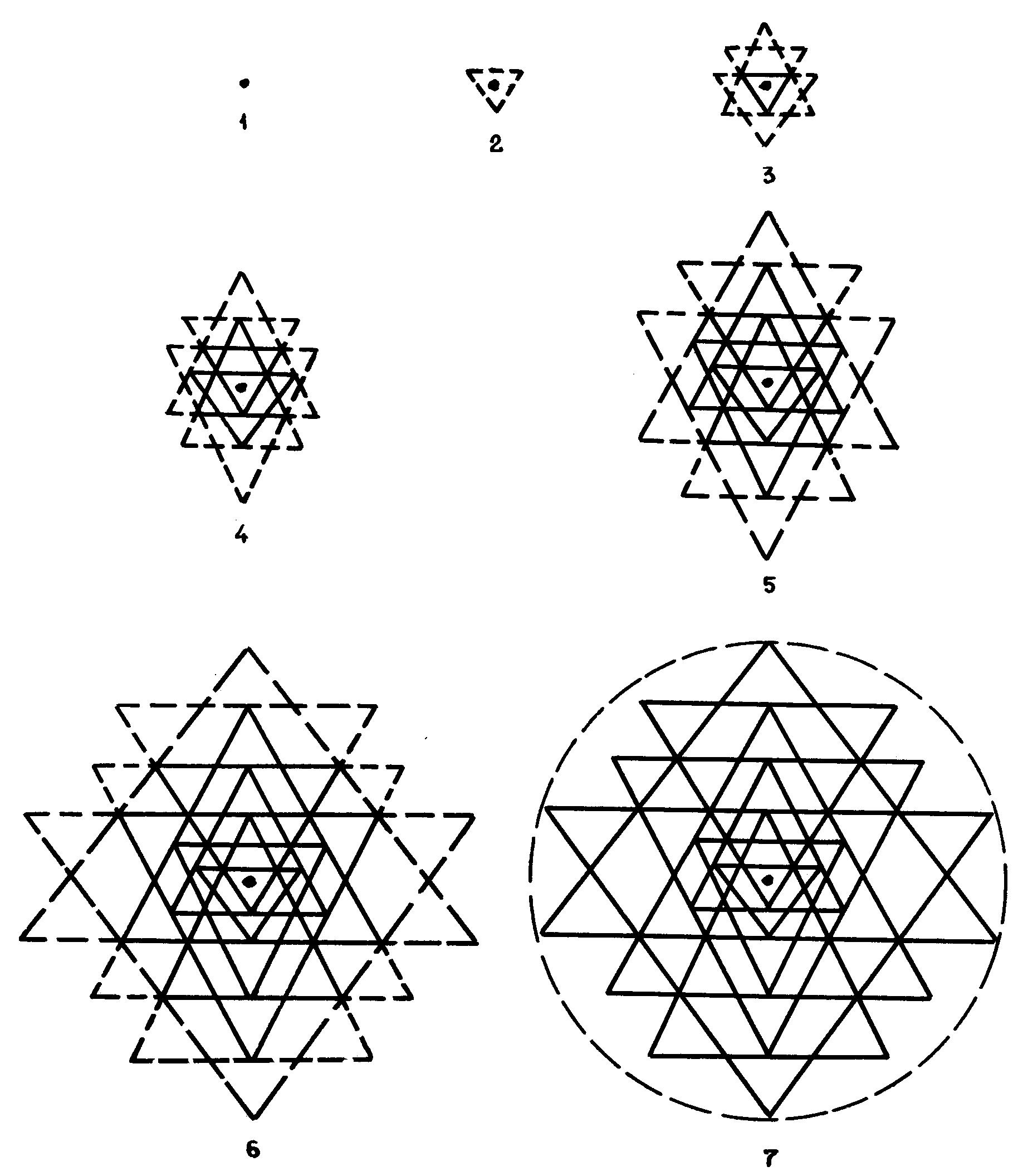
Рис. 6. Традиционный метод умозрительного построения звезды Шри Янтры типа I в порядке творения (srsti-krama)

        Копирование. Для этого типа изображений известно описание традиционного метода копирования [14], согласно которому (рис. 5) вертикальный диаметр внешнего круга звезды предварительного делится на 48 равных частей, после чего проводятся горизонтальные линии на уровне порядковых делений 6, 12, 17, 20, 23, 27, 30, 36, 42, после чего через полученные точки однозначно дорисовываются остальные линии. Однако этот эвристический метод даже для такого упрощенного типа изображений не обеспечивает (даже в визуальном восприятии и при малом размере фигуры) совпадение некоторых точек пересечения.
        Согласно другой схеме копирования (приведенной впервые Генрихом Циммером [2]) звезда Шри Янтры образуется посредством последовательного удлинения сторон треугольников, начиная с внутреннего (рис. 6). Но возможность достижения приемлемой геометрической точности при использовании данной схемы крайне сомнительна по мнению ряда исследователей [14,15]. Действительно, в этом случае уже на первом шаге рисования число априорно выбираемых значений (координат точек) значительно больше четырех (то есть больше числа независимых параметров звезды), и на каждом последующем шаге это число увеличивается. Более того, погрешности в положении ранее выбранных точек оказывают все увеличивающийся негативный эффект при последующих построениях. Поэтому разумно допустить, что в данном случае речь шла не о практическом методе рисования, а только о ментальной процедуре визуализации в рамках вышеупомянутого правостороннего ритуала.
        Отметим также, что никакие подобные инструкции не позволяют увеличивать точность конструкции в отличие от вышерассмотренного вложенного итерационного процесса.
        Тип II. Второй тип изображений звезды Шри Янтры (рис. 4б) значительно реже встречается по сравнению с первым типом, и он характеризуется тем, что точка C компонента 2 располагается на внешней окружности, в связи с чем трудоемкость его воспроизведения возрастает до величины: N=b*c*d+c*d+2*d, приближаясь вплотную к своему предельному значению (см. формулу 1). Инструкций по рисованию такого типа изображений в литературе не встречается.
        Тип III. Третий тип изображений звезды (рис. 4в) встречается крайне редко и характеризуется фиксацией точек C и D компонентов 1 и 2 на внешней окружности и использованием дуг овалов или эллипсов вместо прямых. Тем самым, можно предположить, что данные образцы представляют собой плоские проекции некоторого сферического образа, что подтверждается исполнением некоторых экземпляров таких изображений на отчетливо выпуклых поверхностях (такие образцы приведены в [13]).
        Сферическое решение. Сферическое изображение представляется логичным реконструировать следующим образом (рис. 7). Внешняя окружность звезды формируется в виде бокового сечения несущей сферы, и ее положение может быть задано углом aльфа по отношению к оси Z, перпендикулярной к упомянутому сечению. Стороны треугольников звезды представляют собой геодезические линии на сфере (формируются центральными сечениями сферы). При aльфа->0 сферический образ приближается к своему линейному пределу, который обозначим IIIL (III-линейный, точное построение которого мы, собственно, и рассмотрели на рис.2). Знаменательно, что некоторые реальные образцы Шри Янтры типа II приближаются (вследствие близости точки D к внешней окружности) к этому линейному пределу сферического образа (рис. 8, этот образец взят из [16]. Из-за единичности подобного примера мы не выделили III-L в самостоятельный исторический тип изображений. Его минимальная представимость в доступной выборке образцов может быть объяснена предельной сложностью воспроизведения, поскольку для кажущегося более сложным сферического типа III легче скрыть погрешности построения заменой эллипсов на более простые, подобные им кривые, например, овалы) .

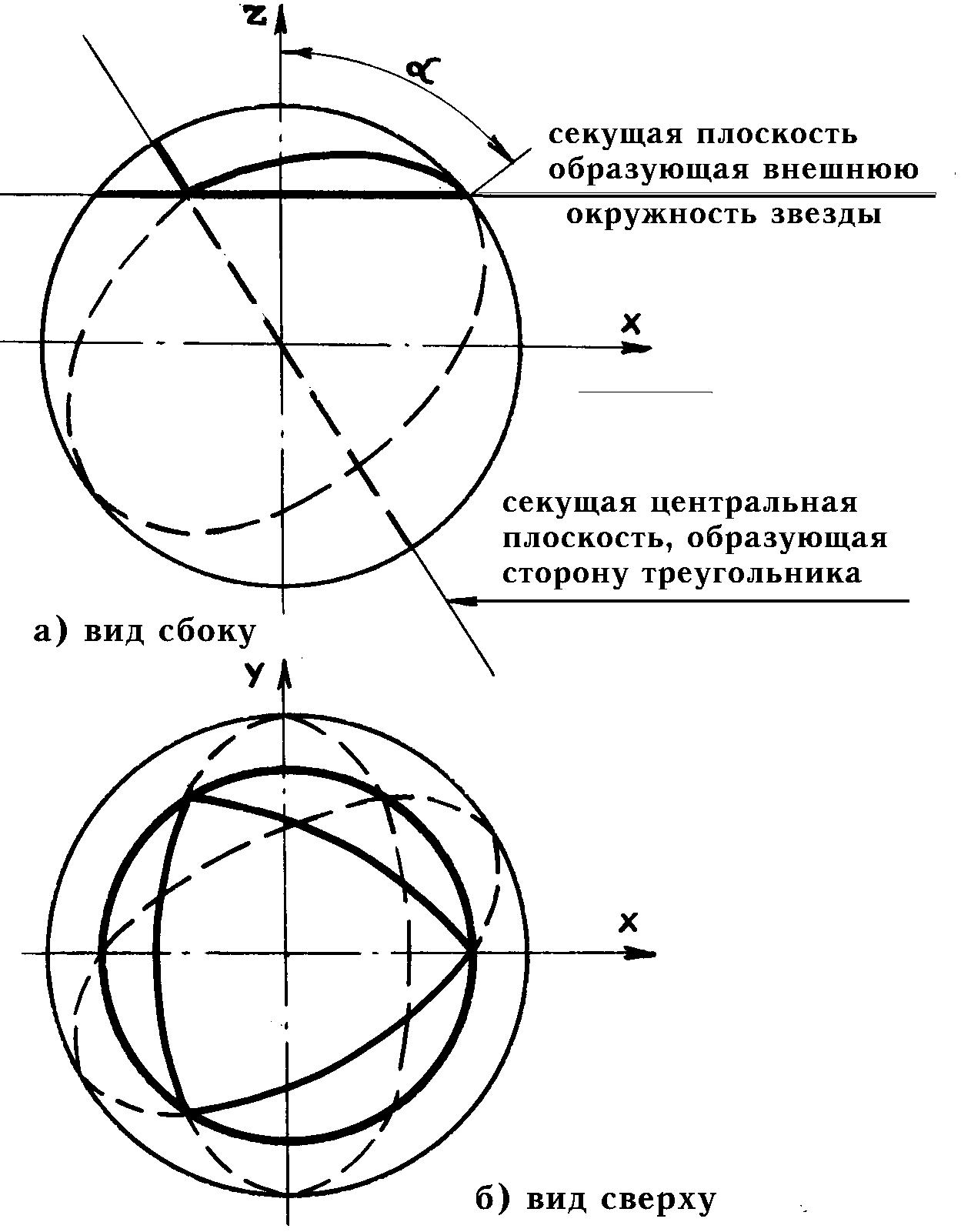
Рис. 7. Принцип сферической конструкции звезды Шри Янтры

        Свойства. Образцы типа III и II-IL описываются полными системами из четырех уравнений от четырех неизвестных (аналогично системе 4). Поэтому их решения могут включать конечное (дискретное) множество действительных корней и, следовательно, эти образцы являются жесткими. Так, если представить звезды этого типа изготовленными из металлических, подвижно сочлененных стержней, то их нельзя деформировать, изменяя положение какого-либо стержня, поскольку переход из одного в другое из допустимых состояний возможен только скачком. С другой стороны, образцы типа I и II описываются неполными системами уравнений (два или три уравнения от четырех переменных из системы 4), поэтому они допускают непрерывное множество решений, и в упомянутой стержневой аналогии их можно непрерывно деформировать, потянув звезду за какой-нибудь стержень.
        Прототип. Таким образом, с математической точки зрения типологический ряд III, IIIL, II, I есть строгая последовательность от общего к частному. Поэтому образец типа III можно рассматривать как гипотетический оригинал, а другие типы звезды можно рассматривать как его последовательные упрощения, возникшие в результате многовекового накопления ошибок копирования с утратой исходных знаний.

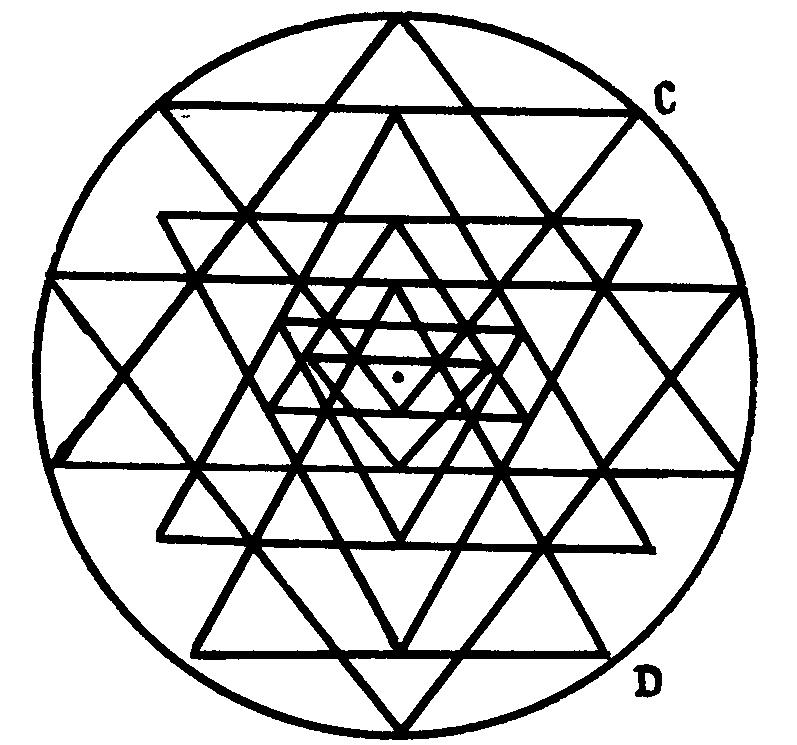
Рис. 8. Образец типа II, приближающийся к плоскому пределу звезды типа III.

        Распространение. Это наше предположение согласуется с имеющимися данными временного и пространственного распространения доступных образцов Шри Янтры (хотя эти данные, к сожалению, из-за полного отсутствия специальных исследований охватывают достаточно небольшой и близлежащий к нам исторический отрезок времени). Так все три известных образца типа III (эти три образца приведены в [13] и [17]) изготовлены не позднее 17 столетия н.э. на металлических пластинах или камне (возможно с использованием достаточно точного метода штамповки с более древних матриц). С другой стороны, образцы типа II и I распределены в более поздних и примыкающих к современности временных интервалах (соответственно, в 17-19 и 18-20 столетиях). Эти изображения обычно выполнены на бумаге или ткани намного менее точным способом ручного рисования. Сравнительная представимость образцов типа III, II, I среди 30-40 доступных различных изображений Шри Янтры может быть приблизительно оценена, как 10%, 20%, 70%. Эти данные также подтверждают большее распространение более современных и более простых изображений.
        Трудоемкость точного сферического воспроизведения звезды Шри Янтры неизмеримо высока в сравнении с плоскими проекциями вследствие использования кривых второй степени вместо прямых. Поэтому крайне сомнительно, что алгебраическое описание (аналогичное системе уравнений 4) может быть получено, вследствие невероятного объема и сложности необходимых алгебраических преобразований. В таком случае единственно возможным представляется вычисление отдельных корней численными методами и изображение звезды с использованием средств машинной графики (как известно, эллипс можно нарисовать только поточечно, поэтому в подавляющем большинстве учебников в качестве иллюстраций приведены не собственно эллипсы, а близкие к ним овалы).
        Сферическая динамика. Как показали компьютерные исследования, найденное численное решение (один из корней) проявляет динамику (рис. 9), вызывающую аналогию с интерпретацией Шри Янтры, как схемы эволюции и инволюции вселенной. Так при увеличении угла a звезда возникает из верхней точки на сфере и распространяется по ее верхней половине до aльфа=90°. Затем (aльфа=90-180°) процесс обращается в свою симметричную противоположенность, то есть — стягивание к нижней точке на сфере. Такое свойство сферической композиции является еще одним косвенным подтверждением в пользу гипотезы о прототипе III Шри Янтры.

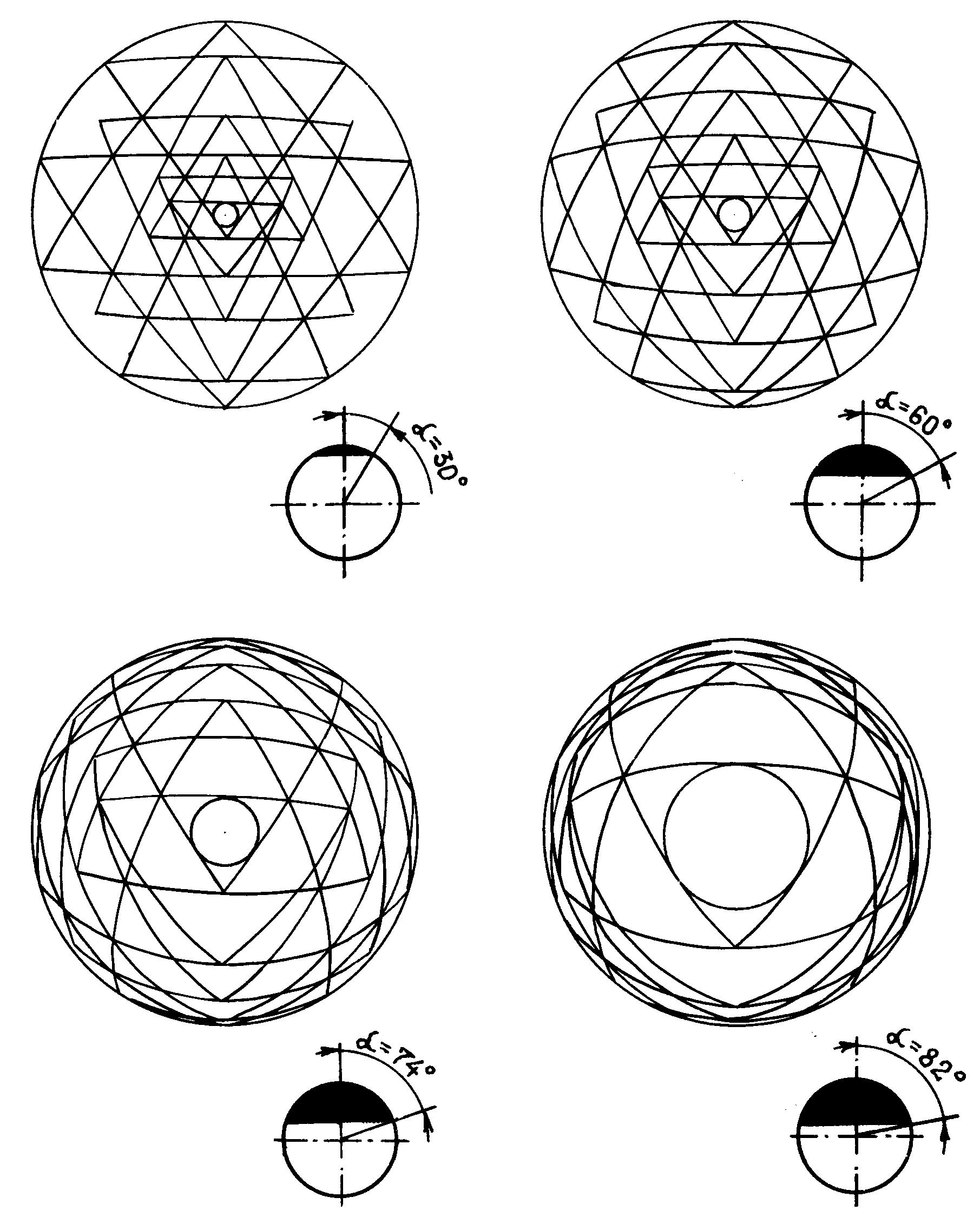
Рис. 9. Динамика изменения звезды Шри Янтры типа III при изменении угла a, определяющего положение на сфере внешней окружности звезды (изображения приведены к одинаковому масштабу)

        Числовые корреляты. Существование столь сложного для воспроизведения геометрического объекта может натолкнуть на мысль о наличии некоторых простых корреляций в структуре звезды Шри Янтры, которые позволяли в древности ее воспроизводить примитивными инструментами. Однако при исследовании звезды типа IIIL нам не удалось обнаружить соотношений, с абсолютной точностью выражающихся в целых числах, простых дробях или основных трансцендентных константах. С другой стороны, для звезд типа I и II вследствие их мягкости, если наложить соответствующие ограничения на их степени свободы (координаты точек C и D), то можно добиться наперед заданного числового соотношения между выбранными сторонами треугольников (подобная попытка для отношения «золотое сечение» и числа p для звезды типа I была принята в [14], и эта работа до сих пор (1999г.) является единственным, нам известным математическим исследованием Шри Янтры).

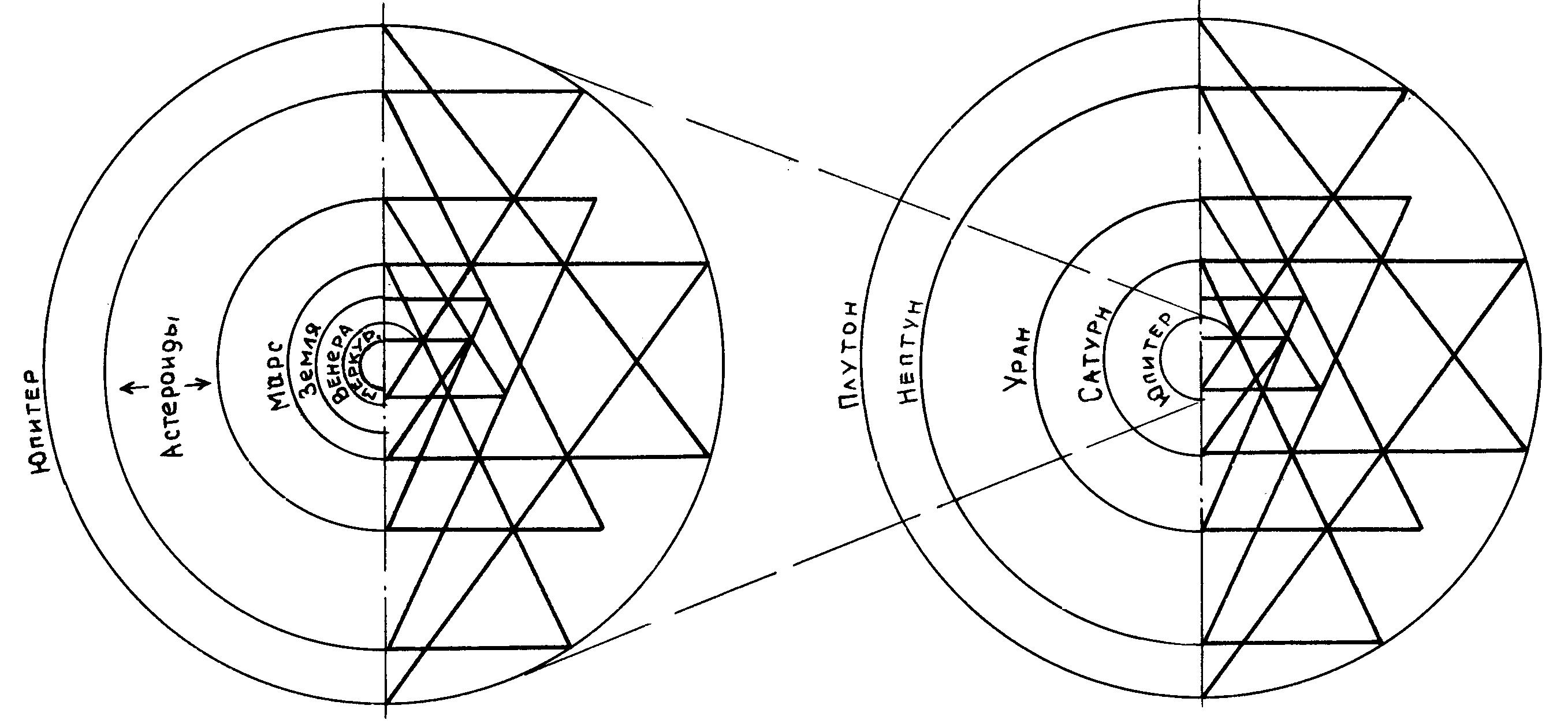
Рис. 10. Астрономическая интерпретация В.Сагмейстера

        К.х.н. Г.П.Овсяников из Саратова провел детальное исследование (для различных мягких вариантов звезды) геометрических коррелятов и обнаружил множество впечатляющих соотношений, близких к числу p, основанию натуральных логарифмов, базисным параметрам лунно-солнечного календаря и астрономическим циклам. В частности, он предложил соотношение yB=yA/e, которое отличается от точного значения всего на 1.3%. По полученным им результатам была подготовлена специальная подробная статья для того же журнала, которой также не суждено было пробиться в печать.
        Итеративное черчение. Вторым направлением исследований было применение итеративно-чертежной техники для получения максимально точных изображений большого размера.
        Абсолютный рекорд в масштабе изображений (при упрощающем отказе от соосности внешней и внутренней окружностей) принадлежит рабочему из г.Батайска Ростовской обл. Н.И.Росохатому, который при диаметре 1 метр добился точности построения  в 2.01% с положением горизонталей на уровне отметок 131, 273, 365, 410, 463, 533, 610, 711, 884 мм, затратив на итеративные перестроения сутки непрерывного труда, что может служить начальной точкой отсчета для оценки необходимых временных затрат на итеративное черчение (Здесь и далее точность построения оценивалась по максимальной погрешности (несовпадение в пересечениях линий) в трех критических точках (A, A’, B) и выражалась в процентах от радиуса R внешней окружности. Здесь мы решили не учитывать погрешность в точке E (вследствие несоосности окружностей), поскольку она обычно подавляюще превосходила остальные погрешности и составляла 3-5%. Проверки выполнялись на компьютерной программе, поэтому приводимые значения могут отличаться от заявленных самими авторами.).
        Далее, инженер из Ленинграда С.В.Морозов пришел к выводу, что обычные чертежные инструменты не позволяют производить достаточно точные построения при диаметре более 490 мм. В результате для диаметра 490 мм он получил расположение горизонталей на уровне отметок 57, 131, 178, 202, 229, 266, 307, 360, 443 мм с высокой точностью построения 0.667%. Он же подметил следующую эмпирическую закономерность: 57+443=500, 131+360=491, 178+307=485, 229+266=495, то есть сумма ординат противолежащих горизонталей с точностью до 2% близка к величине радиуса внешней окружности.
        Продолжая данное направление, В.Э.Смирнов из Уфы также предположил наличие некоторых простых "магических чисел" или соотношений в структуре звезды, позволявших в древности ее воспроизводить без особых проблем. В качестве возможного приближения он предложил следующий ряд: R:yC:yA:yB = 146:116:41:15, что обеспечивает лучшую для данного направления точность построения около 0.41%.
        Аналитико-расчетное направление. Третье направление составляли аналитическое расчеты геометрии звезды. Здесь В.Э.Смирнов из Уфы по составленной им фортрановской программе и двух своих геометрических находок (см. ниже) добился точности построения в 0.046% при положении четырех горизонталей на уровне значений: yA=0.281, yD=0.8427023, yC=0.7966(6), yB=-0.1024091.

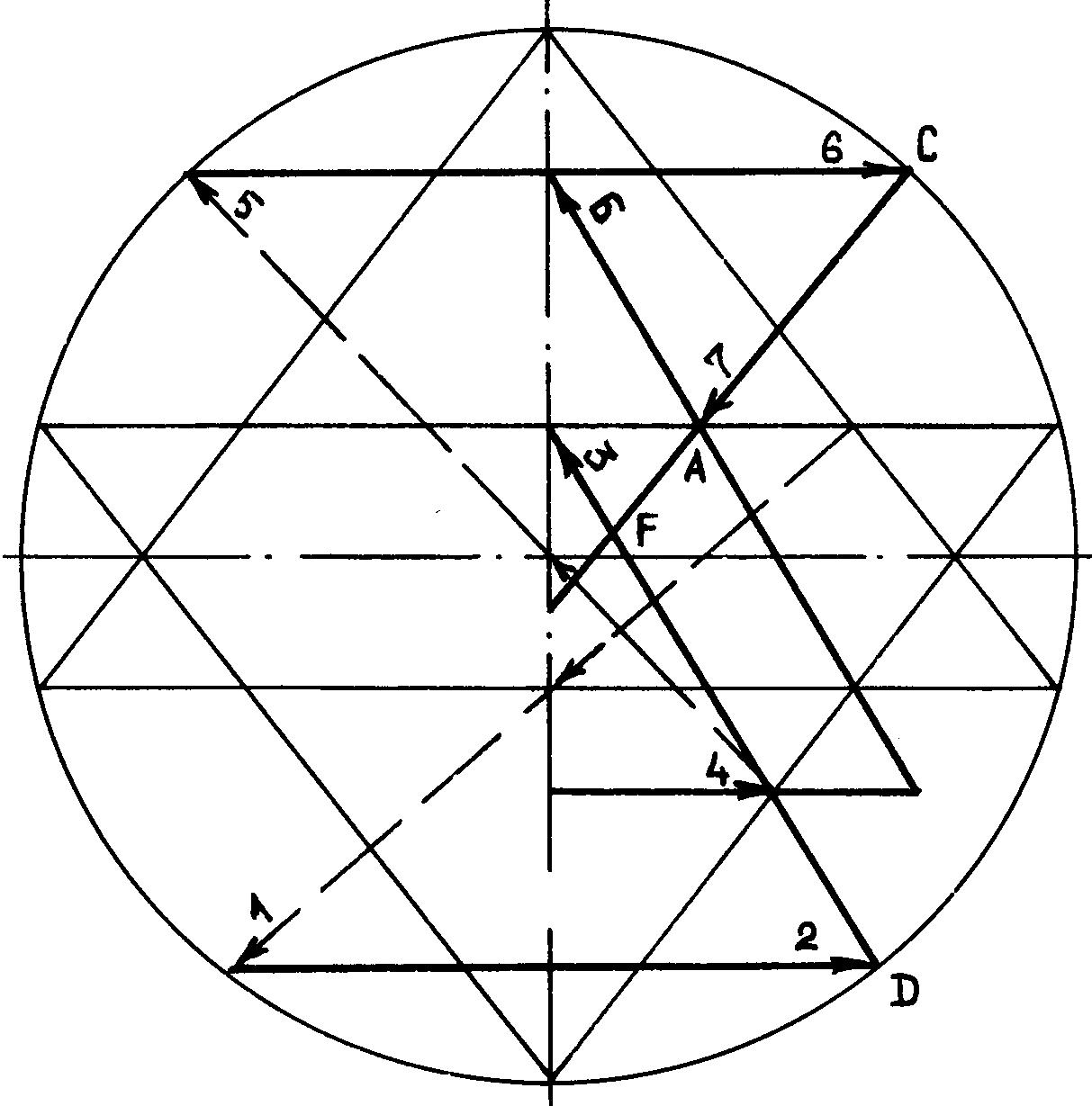
Рис. 11. Метод В.А.Щекоткова и С.Л.Дидыка

        Далее В.Э.Смирнов посредством расчетов на калькуляторе с построением графиков изменения координат в зависимости от величины yA показал невозможность выполнения условия соосности внешней и внутренней окружностей и совпадения угловой точки центрального треугольника с точкой пересечения близлежащих прямых, хотя разность между соответствующими корнями оказалась достаточно мала DyA=0.001.
        Особо в этом направлении следует отметить академически тщательно выполненную работу ветерана Великой Отечественной войны, ст.н.с. Сухумского физико-технического института, к.т.н. Е.С.Ямпольского, который аналитически вывел формулы для всех горизонталей Шри Янтры и в результате расчетов на обычном ручном калькуляторе с использованием метода линейной интерполяции получил значения, только в шестом знаке отличающиеся от значений, вычисленных на мощной ЭВМ.
        Эвристические алгоритмы. Наиболее представительным направлением исследований читателей стал поиск эвристических приемов построения с использованием циркуля и линейки.
        Один из элегантных приемов определения положения точек C и D (при котором точность построения составляет 0.73%) независимо предложили регулировщик проводной связи В.А.Щекотков из пос. Электроизолятор Моск.обл. и студент Харьковского института радиоэлектроники С.Л.Дидык, на основе использования двух вспомогательных секущих, проходящих через точки пересечения больших треугольников (рис. 11).
        Секущую для точки D обнаружил также вышеупомянутый В.Э.Смирнов из Уфы, при этом он доказал из подобия треугольников 1-3-A’ и 2-D-A’, что положение точки D получается в этом случае с абсолютной точностью (рис. 12). При этом итерационный цикл перестроения компонента 1 становится ненужным, и предложенная формула 1 вычисления трудоемкости построения звезды незначительно упрощается: N=bcd+cd+d. Попутно В.Э.Смирнов обнаружил элегантный способ ускоренного итеративного построения компонента 2 (см. также рис. 12).
Все это является дополнительным косвенным подтверждением правильности основного направления наших рассуждений, по крайней мере, относительно приоритетности (или большей близости к прототипу) звезд типа II по сравнению со звездами типа I.
 

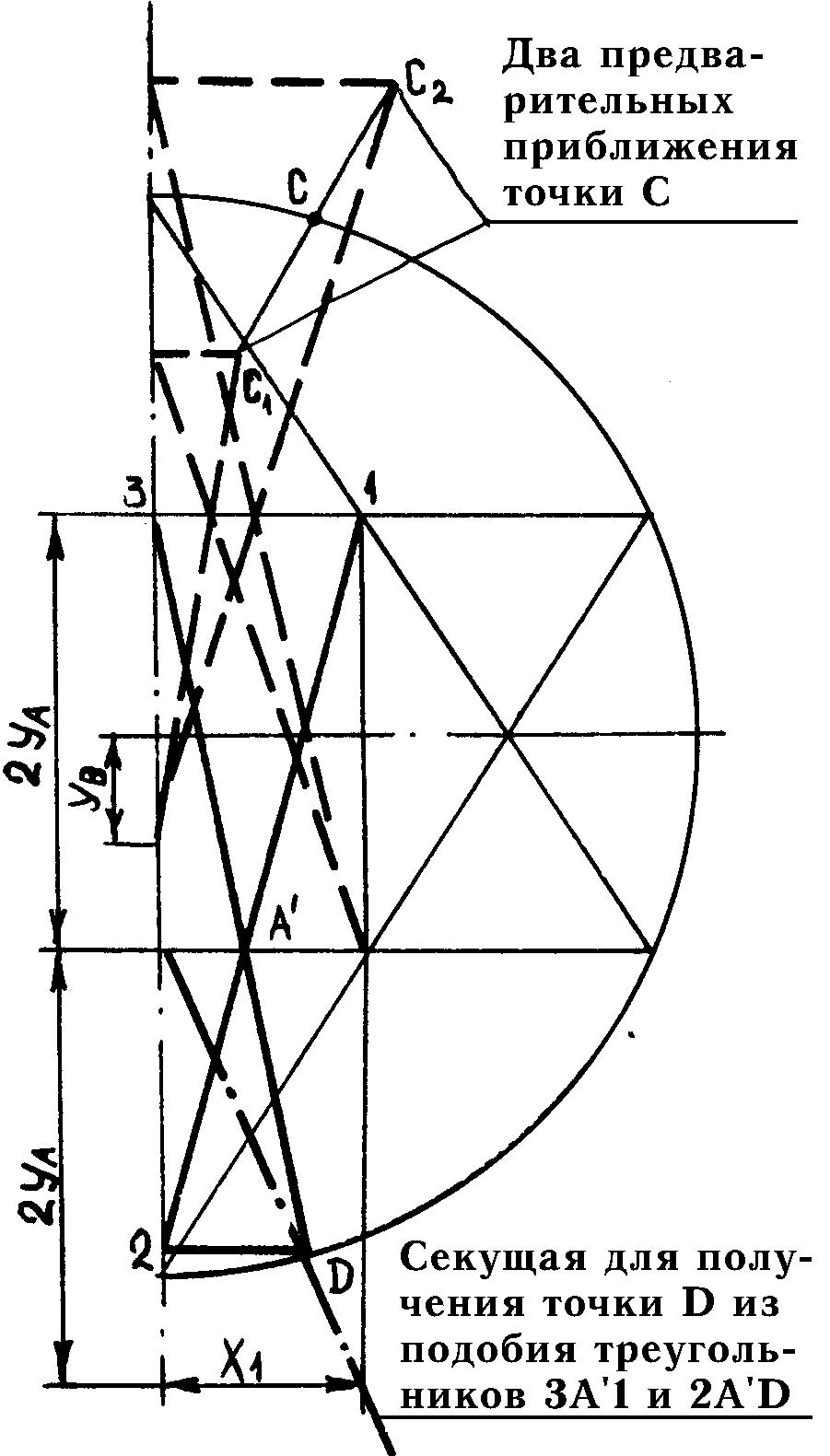
Рис. 12. Метод В.Э.Смирнова

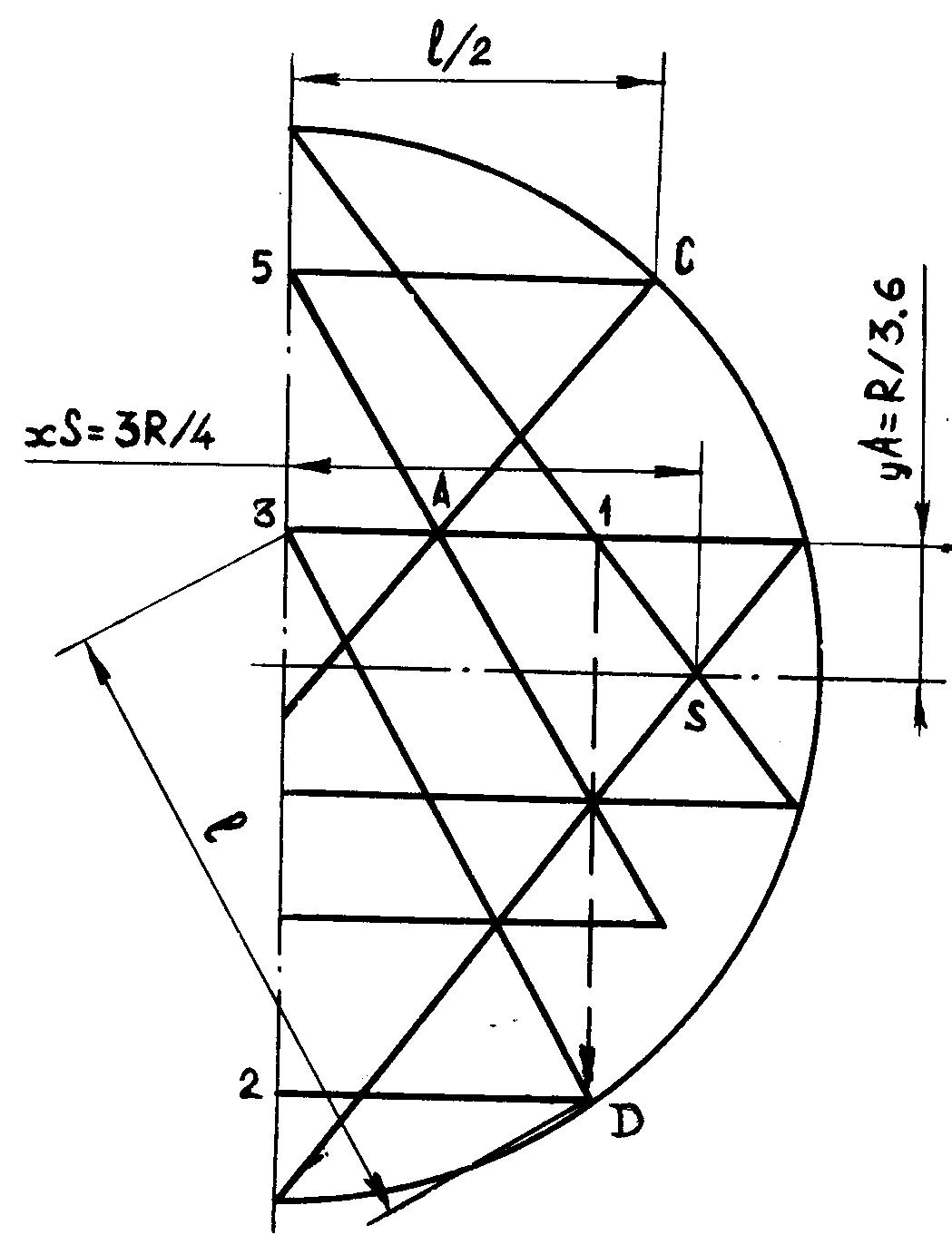
Рис. 13. Метод Г.П.Минаева

        К числу удачных относится и метод каменщика из г.Сумы Г.П.Минаева, (точность=1.6%) с использованием следующих соотношений между длинами L отрезков: L(2,3)=L(3,1), L(5,C)=L(3,D)/2. Он же предложил и два наиболее удачных способа определения параметра yA: yA=R/3.6 и xS=R*0.75 (S — точка пересечения больших треугольников), отличающихся от точных значений на 0.6% и 0.2% (рис.13).

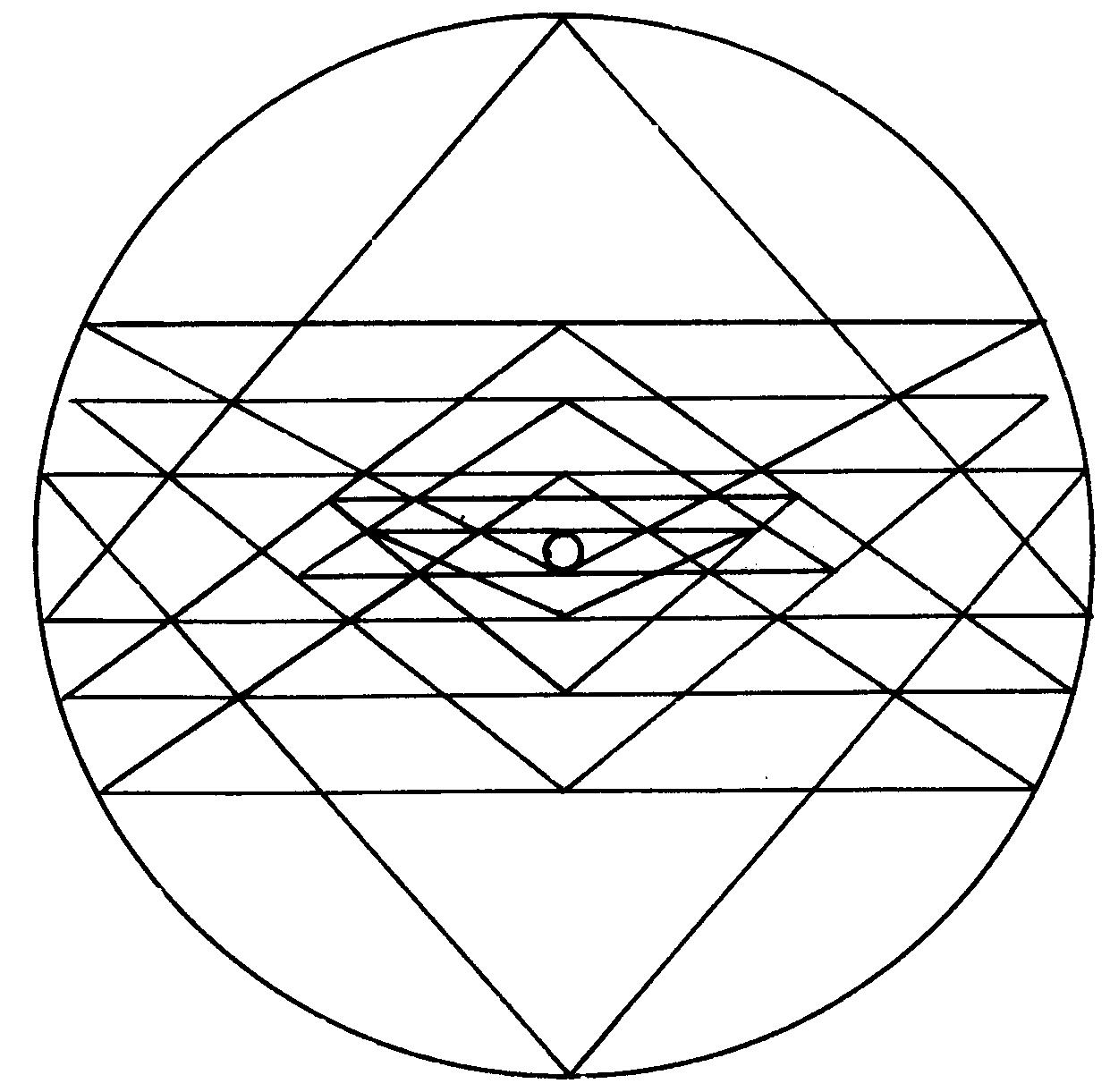
Рис. 14. Предельная форма звезды (памяти Индиры Ганди)

        Большинство читателей упростили себе задачу, игнорируя трудное для выполнение условие соосности внешней и внутренней окружности, сократив трудоемкость своей задачи до вполне приемлемой величины N=bc+c (с учетом доказательства В.Э. Смирнова), и получили за счет этого свободу выбора значения yA.
        Это позволило вышеупомянутым Г.П.Овсяникову и В.А.Щекоткову проследить изменение геометрии звезды при изменении yA и обнаружить предельную форму звезды Шри Янтры при yA=0.1355, касающуюся внешней окружности своими 12 угловыми точками (рис. 14, при дальнейшем уменьшении yA треугольники звезды выходят за границы внешнего круга). Г.П.Овсянников и В.А.Щекотков по приоритету первооткрывателей посвятили этот вариант звезды памяти Индиры Ганди. В этой связи примечательно, что самое первое сообщение о первоначальных результатах математического исследования Шри Янтры появилась в сентябрьском номере 21 журнала Soviet Land (Родина) за 1984 год, который содержал и экстренный выпуск о трагической гибели великой дочери великого индийского народа.
 

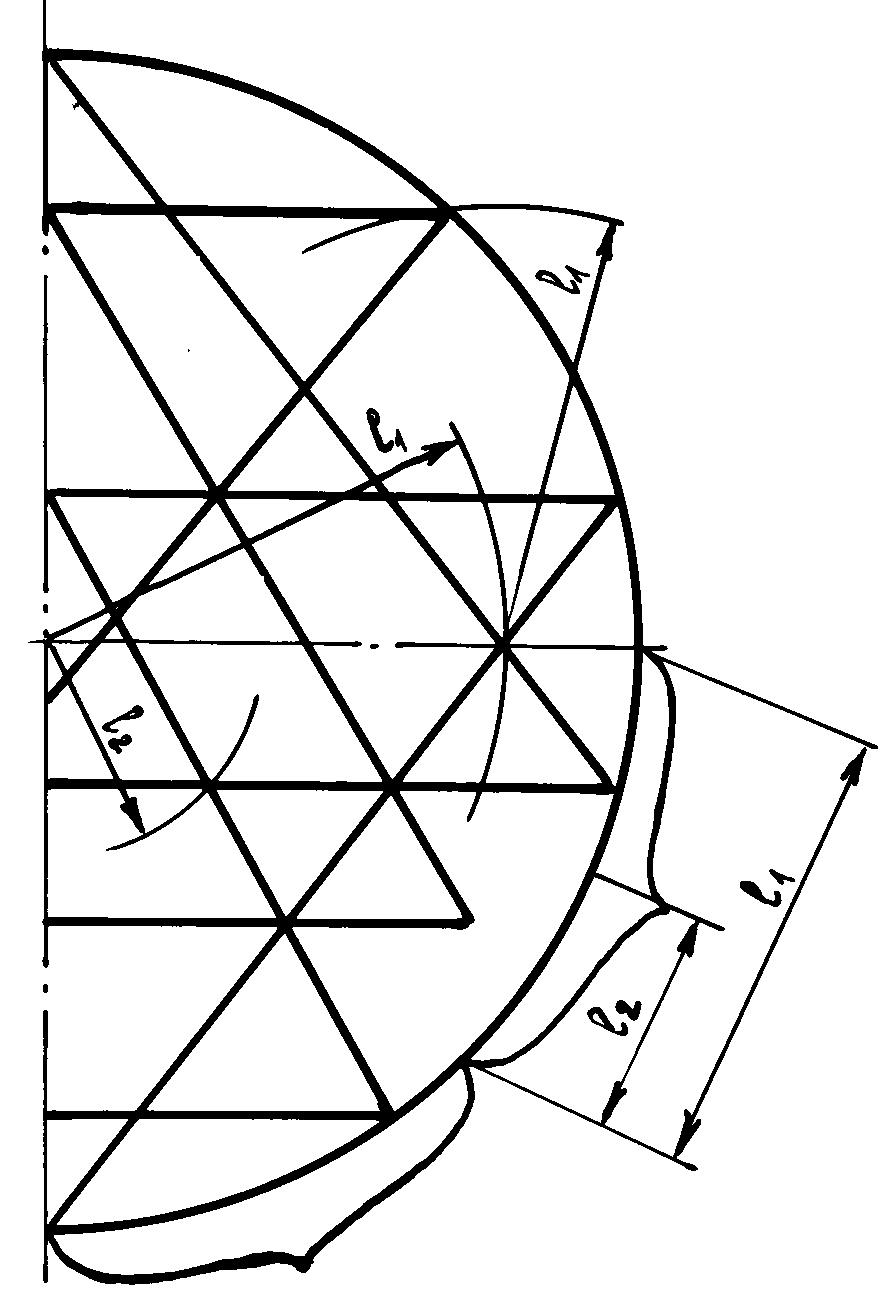
Рис. 15. Метод В.Н.Зайцева

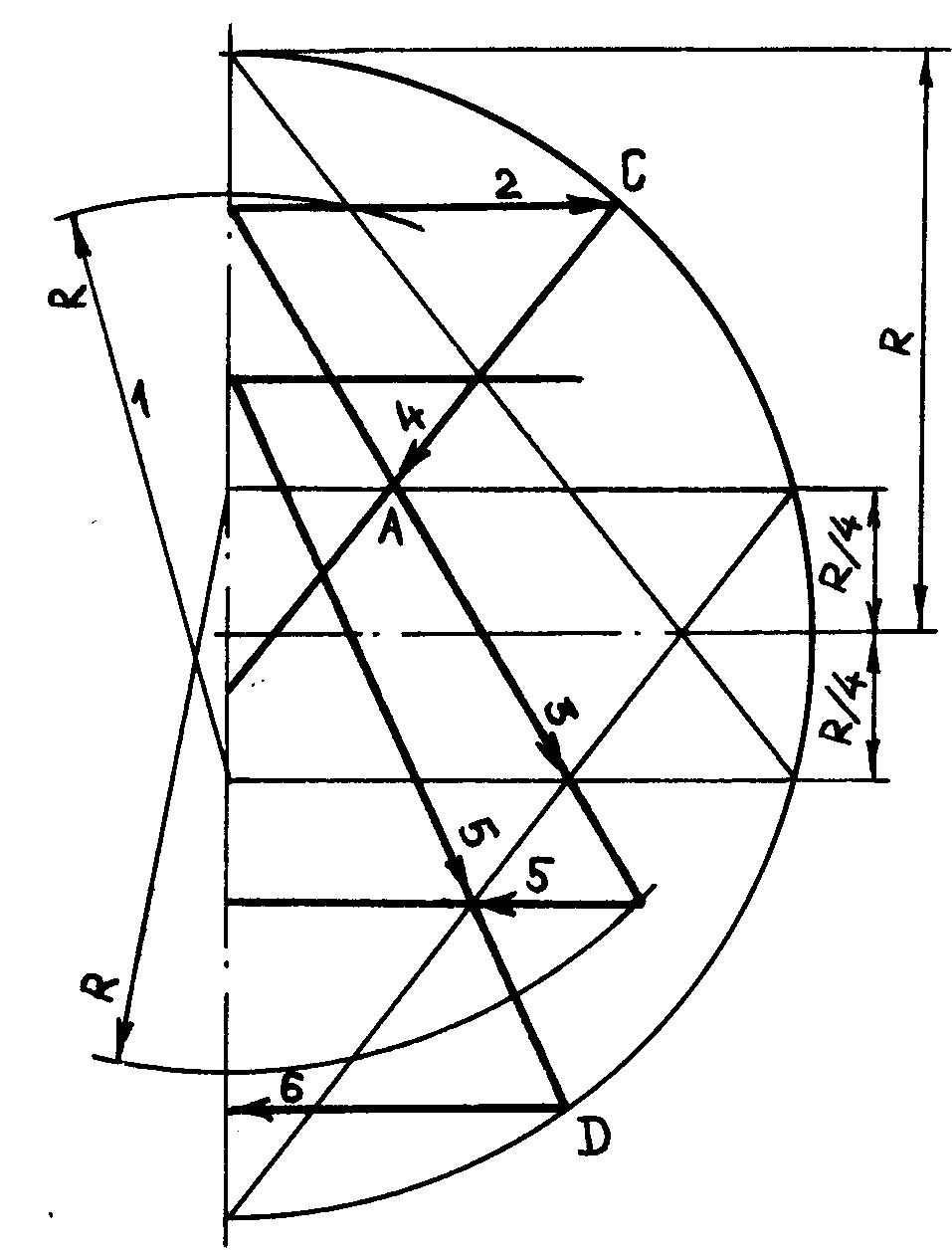
Рис. 16. Метод А.М.Харламова

        Многие авторы в своих работах исходили из содержательных соображений, используя в качестве опорных значений различные структурные компоненты Шри Янтры: лепестки окружающих лотосов, радиус R внешней окружности и др. Первые достаточно точные и оригинальные решения в этом направлении предложили В.Н.Зайцев из Оренбургской области (точность 0.897%, рис. 15) и А.М.Харламов из Евпатории (точность 1.27%, рис. 16).
        Всю полученную корреспонденцию завершало письмо от 25.9.89 В.Г.Шувалова из г.Ефремов Тульской области, который предложил крайне интересное развитие этого направления с опорой на 16-лепестковый лотос, который делит окружность на 32 равные части. Он начал свое построение с произвольного квадрата, на котором построил описанную и вписанную окружности (рис. 17). Затем простым чертежным приемом он дорисовал еще 7 промежуточных квадрата, тем самым получив 32 деления окружности. Далее по полученным точкам были найдены и проведены 4 опорные секущие (на рис.17 они обозначены цифрами 1—4), которые и определили положение базовых горизонталей для точек A,C,D,B. Точность полученного таким методом построения составила 0.135%, что находится на уровне лучших результатов, достигнутых итеративным черчением! Далее, проведя секущую через вершины двух квадратов со смещением на 6 делений (на рис. 17 она отмечена цифрой 5), по касательной к ней В.Г.Шувалов построил окружность для внутреннего 8-лепесткового лотоса и обнаружил, что на характерные точки этой окружности проецируются с хорошей точностью большинство сторон треугольников звезды.
 

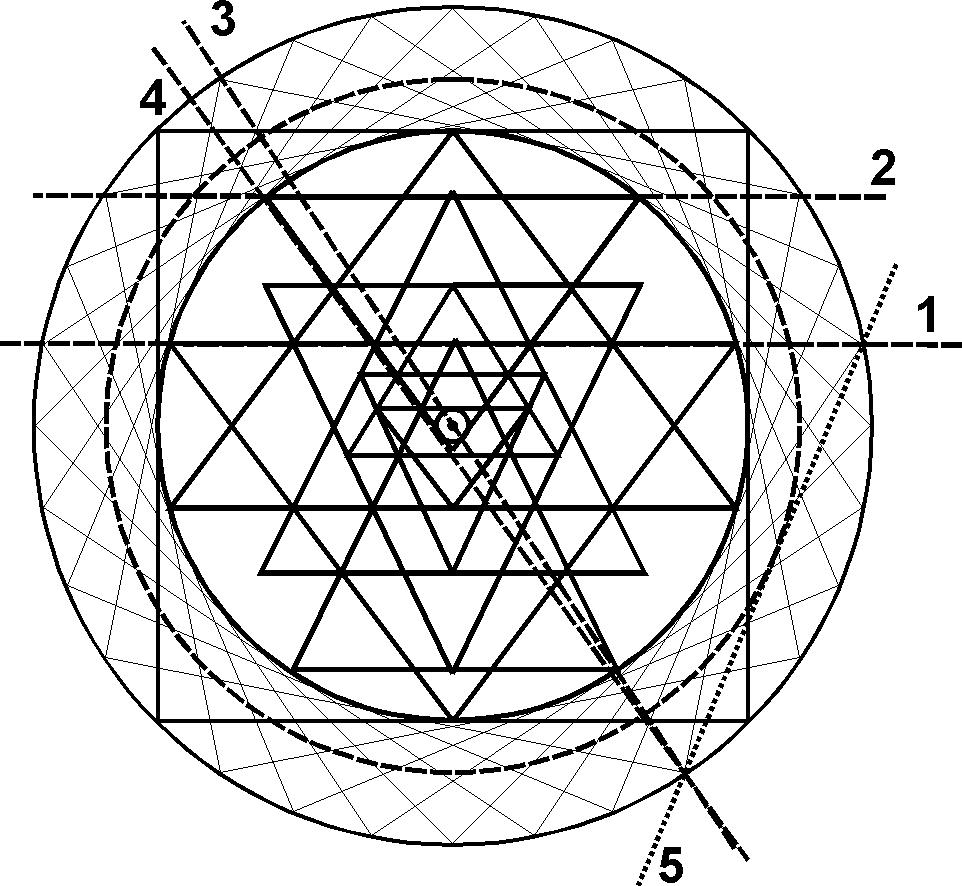
Рис. 17. Метод В.Г.Шувалова

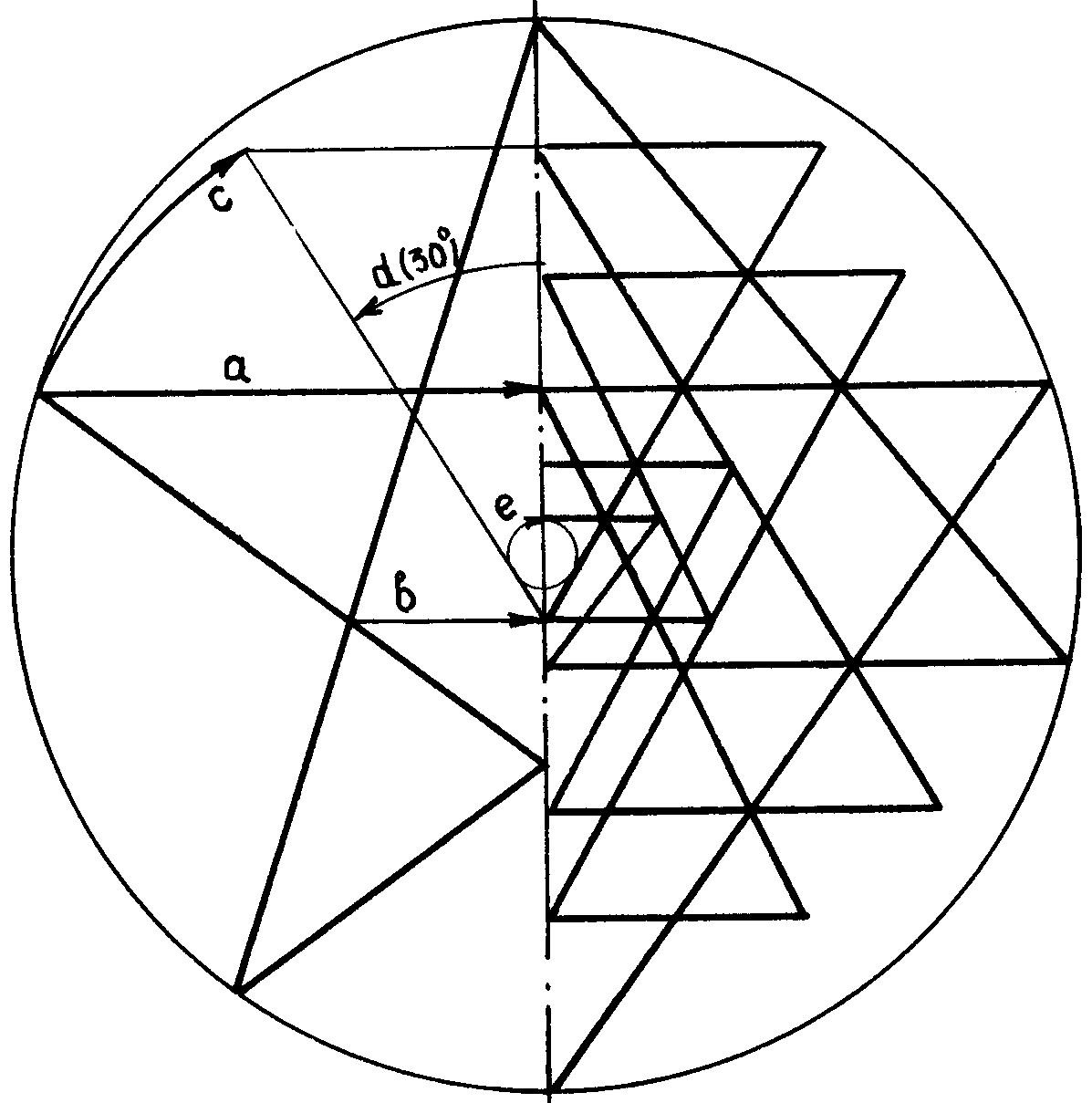
Рис. 18. Метод П.К.Радха

        Другие подходы. Следует отметить, что предположение о существовании прототипа III Шри Янтры, хотя и представляется нам достаточно правдоподобным и обоснованном в первом приближении, но не является неоспоримо доказанным, поэтому оно не отменяет других предположений. Напомним, что жесткий тип звезды может быть получен наложением на ее степени свободы четырех ограничений различного рода (согласно выше выявленной системе четырех параметров звезды Шри Янтры). Мы, исходя из представляющихся нам правдоподобными рассуждений, наложили одну четверку ограничений, на можно, безусловно, найти правдоподобные основания и для наложения других четверок ограничений, в том числе и в рамках звезд типа I и II. Свобода исследователей здесь не может быть ограничена до момента нахождения неоспоримых доказательств относительно какой-либо одной альтернативы. И в этом плане очень интересной представляется работа преподавателя математики П.К.Ратха из индийского города Роуркела в штате Орисса, который построил звезду Шри Янтры на основе пентаграммы (рис. 18), в которой с достаточной точностью выполняются пять наперед заданных независимых условий: точка С, угол a=30°, горизонтали a и b и соосность окружностей (правда, этому способствовал отказ от условия симметричности двух больших треугольников).
        Заключение. Как свидетельствуют вышерассмотренные результаты, существенное продвижение в разгадке тайн Шри Янтры возможно только при участии в этом процессе настойчивых и квалифицированных энтузиастов, способных к разностороннему и свободному творческому мышлению с выдвижением и всесторонней верификацией множества безумных идей.

        Добавление 2013 г. Из появившихся за 15 последних лет публикций по Шри Янтре к ее математическим исследованиям относятся только следующие пять:
        1. Работа индийского исследователя Rao C.S. Sriyantra-A study of spherical and plane forms. Indian Journal of History of Science,1998, V.33(3), pp.203-227, которая достаточно детально исследует сферическое решение Шри Янтры, но не в ее предельном варианте типа III, а в простейшем варианте типа I.
        2. Интернетовский препринт Patrick Flanagan - How to draw a Sri Yantra, 1991, который приводит созданный им после 25 лет исследования вариант построения звезды типа I с использованием золотого сечения и со сылкой на пирамиду Хеопса.
        3. Щекотков Владимир Анатольевич продолжил свои исследования и в 2005 г. создал свой сайт http://altera-pars.narod.ru/S_J/IndxSI.htm, где представил множество своих вариантов звезды Шри Янтры и привел ряд исторических обзоров.
         4. Борис Павлов в 2008 г.создан в редакторе векторной графии MICROSOFT VISIO интерактивную модель звезды Шри Янтры типа I, которую можно разнообразно модифицировать, двигая мышью 4 выделенные горизонтали.
        5. Еще одна работа относится к разряду научных курьезов. Датчанин Gerard Huet в 2002 г. опубликовал статью. Sri Yantra Geometry. Theoretical Computer Science 281 (2002) pp. 609-628. Автор, спустя 15 лет лет после нашей первой публикации и спустя 25 лет после пионерской публикации Bolton&Macleod, рассматривает звезду Шри Янтры типа I с чистого листа без какого-либо знания о предшественниках и приводит "открытые им" уравнения ее линий и условий совпадения точек пересечения. Одно из найденных решений этих уранений без всяких обоснований объявляется "классической Шри Янтрой". Далее без ссылок на предшественников и без доказательства формулируется Теорема о 4-х свободных параметрах Шри Янтры и неизмеримом разнообразии ее возможных форм. Хотя в работе есть отдельный раздел "Библиографический поиск", но в нем не приводится ни один источник по математическому исследованию Шри Янтры. Во остальной 2/3 своего труда автор переписывает описание ритуального значения элементов Шри Янтры из монографии Madhu Khanna, 1975. Все это контрастирует с тем, что на персональной страничке Gеrard Huet приводится список научных трудов из более 107 публикаций и поистине необозримый круг научных интересов и степеней в различных академиях и сообществах: LOGIC: Type Theory; Sequent Calculus; Linear logic; Proof nets; Constructive Mathematics; Automation of Reasoning; Proof Assistants. COMPUTATION THEORY: Semantics of programming languages; Lambda-calculus; Unification; Induction; Categorical models; Sequentiality; Interaction combinators. ALGORITHMICS: Finite-state machines; Regular relations; Transducers; Formal computing; Relational machines. FORMAL METHODS: Specification Languages; Type theoretical frameworks; Program validation; Certification of Safety-Critical Software; Certified Mobile Code. PROGRAMMING LANGUAGES: Functional Programming; ML; Logic and Constraints Programming; Relational Programming. SOFTWARE ENGINEERING:  Literate Programming; Programming Environments; Software Architecture; Extreme Programming. LINGUISTICS ENGINEERING: Computational Linguistics; Lexicon; Morphology; Segmentation; Dependency grammars; Semantics; Pivot Languages; Sanskrit. KNOWLEDGE ENGINEERING:  Semantic nets; Description logics; Mobile truth; Web services; Digital libraries. HUMANITIES and ARTS:  Linguistics; Semiology; Ethnology; Cultural Heritage; Indian Civilization.SOCIAL SCIENCES: Education; Research methodology, evaluation and prospective; International Relations; Sustainable development.LIFE SCIENCES: Modelling and simulation of life; Cerebral and Sensorial functionality.
        Что же, и в научном мире встречаются выбросы в три и более стандартных отклонений, вероятность которых составляет менее 0.27%.
 
 

        Шри Янтра — древнее ритуальное тантристкое изображение, как было показано в [1], обладает крайне сложными геометрическими свойствами. Однако с ним также связана и глубокая и детализованная космогоническая и психофизиологическая интерпретация. Такой дуализм следует из основной тантристкой идеи о тесной взаимосвязи между микрокосмом и макрокосмом.
        Согласно тантристской доктрине [2], каждый из неисчислимых циклов космической эволюции начинается от расщепления исходного единства Шива-Шакти (Высшее Сознание — Высшая Энергия) в виде Космического Яйца, которое мыслится как вневременное и внепространственное нематериальное состояние. В начале этого генезиса появляются категории времени, пространства, причинности и материи, которые затем развиваются во все более сложные и множественные формы. Однако в некоторой точке этот процесс развития обращается в свою противоположность, то есть — в деструкцию или инволюцию, ведущую опять к состоянию неразрывного единства Шива-Шакти. Концентрические уровни Шри Янтры (цепи треугольников, лотосов и линий внешнего квадрата) являются символическим представлением различных стадий этого эволюционно-инволюционного процесса (отметим, что детальное описание этого процесса [2] следует древней интуитивной системе понятий, существенно отличающейся от терминологии, принятой в современной физике и космологии), начинающегося из центральной точки бинду (bindu — единство Шива-Шакти) к внешнему квадрату защиты — бхупуре (bhupura — полное проявление Вселенной), который в свою очередь отделяет упорядоченный мир от окружающего Хаоса.
        Такие древние тантристкие идеи, впоследствии развитые в традиции Пуран, в сравнении с космогоническими мифами и легендами других древних культурных регионов более близко соответствуют современным теориям Большого Взрыва и Горячей Вселенной [3]. Более того, они находятся в рамках так называемой модели пульсирующей Вселенной, которая еще ждет своего экспериментального подтверждения. Тот факт, что такие глобальные космогонические идеи существовали в Древней Индии, представляется экстраординарным, особенно если мы сопоставим его с западной научной мыслью, которая с конца античности и вплоть до второй половины 19-го столетия безмятежно дремала в представлениях о неизменности процессов и явлений буквально во всех природных проявлениях. В доступной литературе мы не нашли удовлетворительного научного объяснения такого уникального древнеиндийского интуитивного прозрения и не встретили даже постановки такой проблемы (подобные аналогии не обсуждаются даже в фундаментальном труде [5], полностью посвященном подобным вопросам).
        Примечание. Напомним, что современная научная концепция глобальной космодинамики проистекала из двух знаменательных событий: в 1922 г. советский математик А.Фридман нашел решения Эйнштейновских уравнений тяготения для нестационарной модели Вселенной, а в 1929 г. британский астроном Э.Хаббл опубликовал результаты своих исследований красного смещения удаленных космологических объектов, интепретируемых им как разбегание галактик. Но эти результаты обрели свое революционное значение только в 1948 г. после создания американским физиком Г.Гамовым теории Горячей Вселенной. Решающим же триумфом явилось открытие А.Пензасом и Р.И.Вильсоном предсказанного этой теорией реликтового космологического радиоизлучения (Нобелевская премия по физике 1978 года, см. в [4]).
        С другой стороны, в соответствии с вышеупомянутой основой тантристкой доктрины концентрические уровни Шри Янтры (последовательности треугольников, лепестков лотоса и линий обрамления) обозначают различные энергетические узлы или чакры, располагающиеся вдоль позвоночного столба человека, начиная с нижней, копчиковой чакры Муладхара (сопоставляется бхупуре Шри Янтры), где локализуется энергия Шакти, именуемая Кундалини, до головной чакры Сахасхара (сопоставляется центральной точке — бинду Шри Янтры), где располагается принцип сознания Шивы.
        Ритуальная практика тантризма предполагает использование Шри Янтры, главным образом, как обобщенного плана или карты для инициации и управления движением Кундалини вдоль позвоночного столба. Здесь элементы Шри Янтры выступают как обозначения различных этапов такого процесса и необходимых действий со стороны адепта. Поскольку движение Кундалини ассоциируется о космогенезом, считается, что при достижении энергией Шакти головной чакры (соединении Шакти с Шивой) адепт обретает расширение сознания, приобретая прямое знание об Универсуме.
        Ритуал созерцания Шри Янтры может происходить по правосторонней спирали в двух направлениях: от центральной точки к периферии (в порядке творения Универсума) и обратно (в порядке свертывания Универсума). Последователи  «правосторонней» школы тантры придерживаются эволюционного порядка рассмотрения Шри Янтры в противоположность последователям «левосторонней» школы тантры, придерживающихся инволюционного направления.
Локализация чакр соответствует важнейшим узлам и сплетениям центральной и периферийной нервной системы [6], что указывает на глубокие знания древних об анатомии и физиологии человека, учитывая, что такие представления в западной науке сложились лишь к началу ХХ века. Вместе с тем, прокламируемая тантрой динамика Кундалини до настоящего времени не находит прямых аналогов в известных психофизиологических процессах.
        Представляет интерес проанализировать с современных позиций, благодаря каким свойствам и каким физиологическим причинам Шри Янтра приобрела такое важное значение в ритуале. Нетрудно заметить, что вся ее геометрическая композиция отличается некоторой необычной строгой красотой и при длительном рассмотрении как бы завораживает взор, неотступно притягивая к себе внимание наблюдателя.
        Начнем наше исследование с элементов архитектурной композиции Шри Янтры. Известно, что при обработке зрительной информации в центральной нервной системе важную роль играют специальные нейронные структуры — детекторы элементарных признаков: линий, углов, дуг, цветов и т.д. Преобразование и детектирование зрительной информации, начинающееся еще в сетчатке глаза, продолжается в коленчатом теле и завершается в зрительной (затылочной) коре больших полушарий. Уже в структуре коленчатого тела (специальное подкорковое образование) содержатся примитивные детекторы, реагирующие на появление в зрительном поле пятен в виде концентрических кругов пропорционально степени их контраста. Зрительная кора является основным пунктом преобразования информации и имеет по последним данным [7] колончатую структуру, где каждая вертикальная колонка нейронов отвечает за выполнение строго определенной операции преобразования-детектирования. Из зрительной коры расклассифированная таким образом информация поступает уже в ассоциативные области коры больших полушарий (теменные и лобные части), где происходит ее дальнейший, в том числе и семантический анализ и синтез с другими видами информации.
        Почему же при конструировании Шри Янтры выбор пал на использование простейших геометрических фигур и тонов? Как установлено в ходе недавних исследований, треугольник и параллелограмм — то есть основные элементы композиции центральной звезды — являются наиболее устойчивыми геометрическими фигурами, надежно детектируемыми даже при наличии сильных помех и искажений. Так треугольник распознается в 100% случаев при сильном размывании его контуров, а параллелограмм — в 92% случаев, причем процент распознавания падает незначительно даже при частичном разрушении зрительной коры у подопытных животных. Наличие же основных цветовых тонов в раскраске Шри Янтры способствует усилению общего эффекта за счет активации цветовых детекторов, которых существует всего три типа: "черно-белые", "красно-зеленые" и "сине-желтые". Посредством деятельности только этих трех типов детекторов, собственно, и образуется весь многокрасочный зрительный мир человека.
        Таким образом, Шри Янтра содержит элементы, задействующие большинство различных типов нейронных детекторов, что вызывает их совместную активацию и следующее за этим общее изменение психофизиологического состояния человека. Это может привести как к общему перевозбуждению нервной системы, так и к сильному торможению всех процессов, отвечающих за внешнее восприятие. В отношении числа активируемых детекторов Шри Янтра далеко превосходит любую другую янтру, действительно отвечая своему эпитету Великая.
        Переходя к общим архитектурным характеристикам Шри Янтры, прежде всего, отметим повторяющийся, решетчатый тип ее структуры. Изображения такого типа (известные в современных исследованиях восприятия как ритмические решетки и перенасыщенные рисунки [8]), вызывают ряд зрительных иллюзий и быстрое утомление нервной системы. При длительном рассмотрении они действуют аналогично ритмическим световым вспышкам [9], вызывающим билатеральную гиперсинхронизацию альфа-ритма (резонансные явления в нейронной активности коры головного мозга), характерные для неглубоких стадий сна и предгипнотического состояния. Данный эффект может усиливаться благодаря концентрическому характеру узора Шри Янтры, способствующему фиксации взгляда в одной точке. Известно, что одним из основных условий естественного зрительного восприятия является постоянное движение изображения относительно сетчатки глаза. Для поддержания таких условий в зрительной системе имеется механизм периодических скачкообразных движений глаз с малой и большой амплитудой (саккады). Если тем или иным способом принудительно фиксировать изображение объекта на сетчатке, то спустя 20—30 секунд человек перестает его видеть. При фиксации взгляда волевым образом последовательно возникают изменения цветовосприятия, иллюзия движения объекта и кратковременные исчезновения его из поля зрения. Для человека, незнакомого с соответствующими психофизиологическими механизмами, наблюдение таких феноменов может произвести сильное эмоциональное воздействие с приписыванием объекту фиксации внимания сверхестественных свойств.
        Важно также обратить внимание на чрезвычайно удачное соотношение (возрастание) размеров элементов Шри Янтры в направлении центр-периферия. Как известно, сетчатка глаза организована аналогичным образом: в центре находятся клетки с высокой разрешающей и цветовоспринимающей способностью, а на периферии преобладают рецепторы с черно-белой восприимчивостью и низким разрешением. Такая композиция приводит к тому, что каждый тип рецепторов и детекторов работает с максимальной загрузкой и интенсивностью, поскольку воспринимаемые фрагменты изображения изменяются пропорционально размерам их зрительных полей.
        Таким образом, Шри Янтра удачно сочетает целый комплекс свойств, ответственных за специфические психофизиологические воздействия и широко используемых в современных терапевтических суггестивных методиках.
 

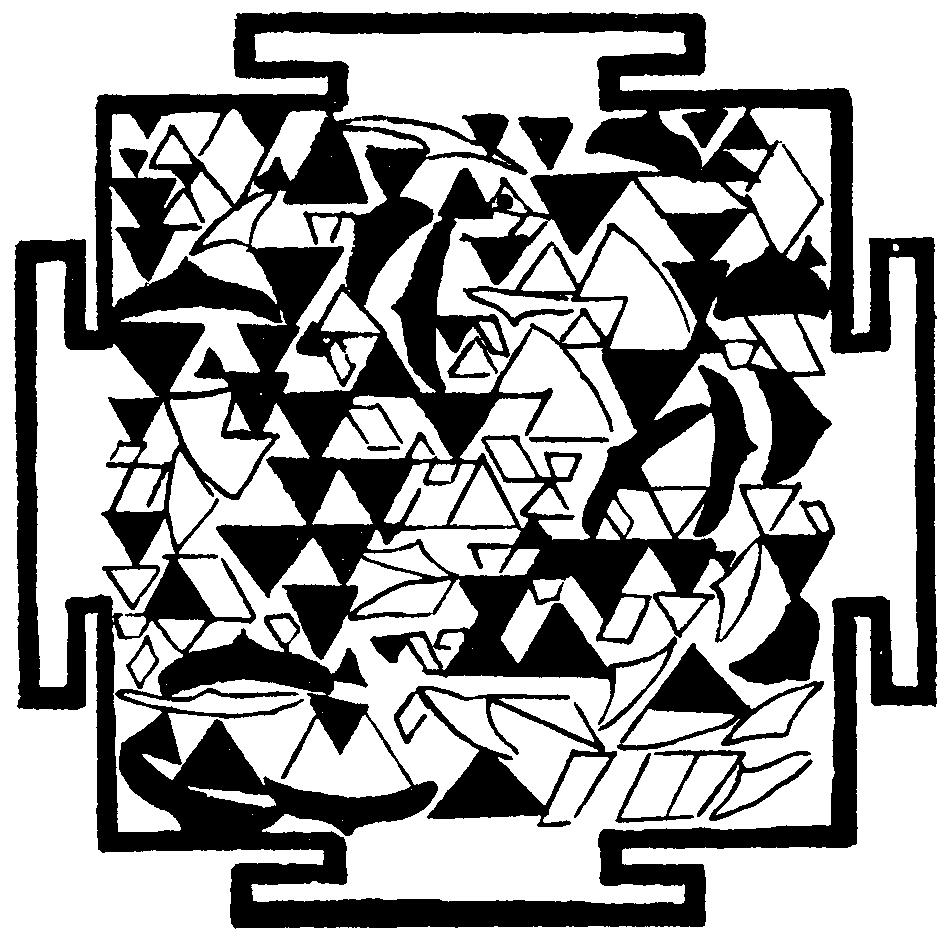
а) псевдоянтра

б) лучи

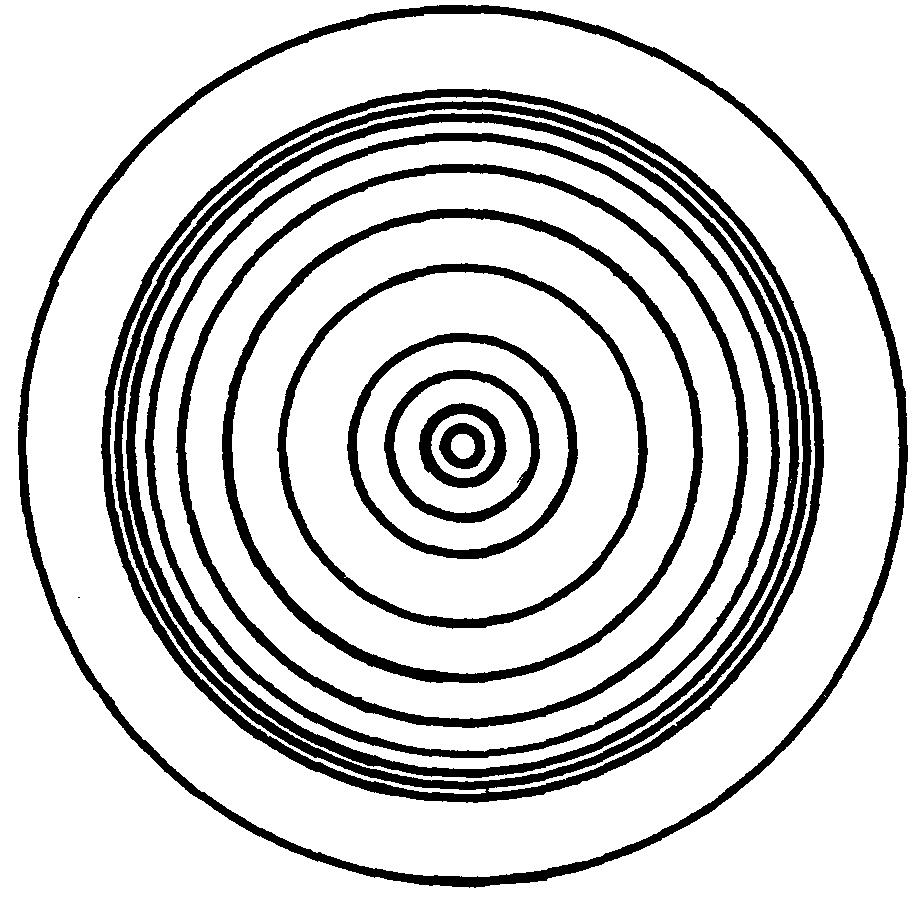
в) круги

        Для проверки рассмотренных предположений на кафедре высшей нервной деятельности Биологического факультета МГУ под руководством Д.М.Рамендик было проведено экспериментальное исследование, в котором испытуемым-добровольцам предъявлялось цветное изображение Шри Янтры с задачей фиксации взгляда на ее различных элементах по команде экспериментатора (длительность каждой фиксации составляла 1 минуту). В качестве контрольных предъявлялись еще три изображения (рис. 1): концентрические окружности, проведенные на соответствующих уровнях Шри Янтры, центрально-сходящиеся лучи и цветной рисунок, полученный перемешиванием элементов Шри Янтры в плоскости изображения по случайному равномерному закону (псевдоянтра). Целью этих предъявлений была проверка реакции на отдельные элементы архитектуры Шри Янтры, могущих иметь решающее стимульное значение. Для чистоты эксперимента в качестве испытуемых привлекались лица, не знакомые с релаксационными и медитационными методиками, и им не сообщалось ни о характере предъявляемых изображений, ни о целях эксперимента. При этом мы исходили из того, что если некоторый объективный и универсальный эффект действия Шри Янтры имеет место, то он должен проявляться и в самых ординарных условиях. Эксперименты сопровождались записью электроэнцефалограммы (ЭЭГ) левой и правой затылочных (зрительных) областей и движения глаз — электроокулограммы (ЭОГ).
        Делая небольшое отступление, отметим, что регистрация и анализ электрической активности мозга является одним из самых точных способов определения функционального состояния или уровня бодрствования [10], характеризующего активность поведения человека, связанную с уровнем тонуса, с активностью нервных центров. В состоянии пассивного бодрствования (человек сидит в удобной позе с закрытыми глазами и не занимается умственной работой) в ЭЭГ наблюдается преобладание колебаний, близких по форме к синусоиде, с частотой 8-12 герц и амплитудой 30-80 микровольт (так называемый альфа-ритм). При снижении уровня бодрствования (дремота) появляются и более низкочастотные колебания. При напряженной умственной работе с открытыми глазами возникает так называемая десинхронизация — частые низкоамплитудные колебания без четко выраженного ритма (10-20 микровольт с частотой 14-30 герц, называемый бета-ритмом). Альфа-ритм может возникать и при открытых глазах, но в эти моменты способность к восприятию внешних сигналов снижается. Имеются данные о том, что в состоянии самоуглубления или медитации в ЭЭГ также преобладает альфа-ритм, и даже могут возникать более медленные ритмы [11] вплоть до полного выполаживания ЭЭГ.
        Во всех проведенных экспериментах реакция на Шри Янтру кардинально отличалась по характеру и интенсивности от реакции на контрольные изображения. При этом наблюдались два прямо противоположных явления. Для одних испытуемых, на которых по их отзывам Шри Янтра производила умиротворяющее воздействие, было характерно быстрое восстановление альфа-ритма, свидетельствующее о снижении уровня бодрствования и уменьшении контакта человека с внешней средой. У других же испытуемых, которых Шри Янтра раздражала, наблюдалось резкое угнетение альфа-ритма, характерное для напряженно-возбужденного состояния, с интенсивным движением глаз, несмотря на настойчивые требования экспериментатора сконцентрировать взгляд. В таблице 1 на двух категорий испытуемых показано среднее процентное содержание альфа-ритма в спокойном состоянии с закрытыми глазами до опыта, во время предъявления изображений и при закрытых глазах после предъявления Шри Янтры.

        Из таблицы видно, что испытуемые обоих типов начинали из близких функциональных состояний, и в обоих случаях процесс рассматривания изображений вызвал общее возбуждение. Но у спокойных испытуемых это возбуждение было минимально (много альфа-ритма) при предъявлении Шри Янтры. Кроме того, при закрывании глаз после восприятия Шри Янтры количество альфа-ритма уменьшалось, хотя оно обычно при закрывании глаз увеличивается. У возбужденных испытуемых общая активность была значительно сильнее в продолжение всего эксперимента, но особенно — при предъявлении Шри Янтры. После закрывания глаз возникало восстановление альфа-ритма, превосходящее исходный фон (своеобразная отдача).
        Таким образом, Шри Янтра демонстрирует возможности эффективного изменения фонового психофизиологического состояния человека как в сторону успокоения и расслабления, так и в сторону общего возбуждения, при этом эффективность воздействия определяется не отдельными особенностями изображения, а всей их совокупностью. В этом отношении Шри Янтру можно считать уникальным композиционным решением. Характер воздействия Шри Янтры может определяться как индивидуальными особенностями нервной системы человека, так и начальной психофизиологической предустановкой и мотивационными факторами. Тем самым, многовековой практикой в древности удалось создать в форме Шри Янтра чрезвычайно эффективный и направленный инструмент, применимый как для достижения требуемого состояния за счет формирования соответствующей предустановки, так и для отбора индивидуумов с желательным типом нервной системы.
        Несмотря на отмеченную уникальность Шри Янтры, ее основные элементы: треугольники, дуги, контрастно окрашенные поля, площадки и т.д., встречаются и в других ритуальных изображениях, причем не только в различных вариантах тантристских и буддистских янтр и мандал, но и в других религиях: в мусульманской филигранной, монументальной и ковровой вязи, в украшениях бубнов и одежды алтайских шаманов, среди кабалистистических знаков, в христианской иконографии и т.д. Подобный Шри Янтре узор из треугольников прослеживается также в раскраске сферических поверхностей среднеазиатской керамики [13] эпохи неолита и ранней бронзы (3-5 тысячелетие до н.э.), что свидетельствует о возможности существования широкой культурно-исторической общности, учитывая что традиция изображения янтр, по-видимому, восходит к ритуальному символизму культур Хараппа и Мохенджо-Даро, где обнаружены многочисленные печати с геометрической символикой. И здесь, безусловно, имеется широкое поле, как для исторических, так и для психологических исследований.
        При всем различии упомянутых культур и ритуалов, в них присутствует стремление создать у участников некоторое общее психофизиологическое состояние, которое люди объективно идентифицируют, но не могут, как правило, выразить, описать в словесной форме. Оно характеризуется углубленным сосредоточием на каком-либо объекте вовне или внутри человека при отвлечении от всех других сигналов, вплоть до полного отключения. Одновременно возникает ощущение сверхширокого видения, сверхпонимания мира (именно — всего мира, а не ближайшего окружения), а также чувство наличия неких сверхвозможностей, сверхвласти над вещами и явлениями. Такое мировосприятие нередко имеет место у людей, у которых вследствие патологического процесса, хирургического вмешательства или применения фармакологических веществ левое полушарие коры головного мозга заторможено или отключено [14].
        Согласно данным современной неврологии, у большинства людей (праворуких, у леворуких же обычно соотношение полушарий противоположенно рассматриваемому) левое полушарие коры головного мозга специализировано на функциях, связанных с речью и аналитическим, дискретным, логическим мышлением. Правое же полушарие осуществляет целостное восприятие мира в невербальной (наглядной, звуковой и т.д.) форме. Можно сказать, что левое полушарие имеет дело с предметами постольку, поскольку они имеют имена, и действует с ними по известным логическим правилам, выраженным словами (его деятельность окрашена положительными эмоциями). Правое же полушарие имеет дело с самими предметами во всем их многообразии и оперирует с ними в соответствии с их реальными или воображаемыми свойствами независимо от того, известны ли имена этих свойств и действий (его деятельность эмоционально нейтральна или окрашена отрицательно).
        В норме полушария тесно связаны между собой и постоянно взаимодействуют, причем левое полушарие доминирует над правым. Работа правого полушария и подкорки (где тоже ведется специфическая переработка информации), остается обычно скрытой от самого человека, она проявляется в виде интуиции, актов творческого прозрения и т.д. В таких случаях решение приходит раньше, чем его формулировка. Часто человеку приходится тратить немало усилий на то, чтобы сделать понятным для других (вербализировать) явление, абсолютно ясное ему самому. Ярким примером этих феноменов могут служить высказывания выдающихся математиков о механизмах своей творческой деятельности [15, 16].
        Эксперименты показывают [17], что преимущественная активация правого полушария возникает при восприятии сложных, но монотонных, гомогенных изображений, ритмических низких гласных звуков, а также при общем расслаблении, переходящем в легкую дремоту. Именно эти элементы, как отмечено выше, присутствуют во многих ритуалах. Характерно, что процесс сосредоточения на янтрах всегда сопровождается повторением мантр, в которых преобладают протяжные гласные звуки и глухие согласные. Тем самым задействуется еще один высокопропускной канал передачи информации — слуховой, изучение дополнительного эффекта включения которого представляет, безусловно, интересную задачу для исследований. Добавим, что поскольку все элементы Шри Янтры связаны с определенной философско-мировозренческой семантикой, в процесс сосредоточения вовлекаются и высшие отделы коры головного мозга, что приводит к координированию и усилению общего психологического эффекта. В наших исследованиях действие указанных факторов совершенно не учитывалось.
        В результате торможения левого полушария и активизации правого знания о мире, имеющиеся у человека, предстают перед ним в своем естественном многообразии и к тому же лишенными привычных оболочек слов и заученных правил действий. А способ, каким человек интерпретирует этот мир, какие фантазии в него привносит, зависит от имеющейся идеологии, мировозрения самого человека. Причем, при гиперактивации правого полушария и глубоком торможении левого вся ситуация получает отрицательную эмоциональную окраску. Для создания положительного эмоционального фона необходимо сохранение некоторого оптимального уровня активации левого полушария. С этих позиций становится понятной та ведущая регулирующая роль, которая отводится в восточных учениях наставнику или гуру.
        Для создания измененного состояния сознания с древнейших времен используются два типа ритуалов. В одних случаях это — неподвижность, расслабление, сосредоточение внимания на неподвижном ритуальном изображении, сопровождающееся протяженными звуками (например, медитационная практика). Ритуалы другого типа включают движения в ускоряющемся ритме под резкие звуки и в окружении ритмически повторяющихся и неожиданных зрительных стимулов: раскачивающихся украшений, вспышек огня и т.д. (например, шаманские и колдовские ритуалы). На первый взгляд кажется, что это — две совершенно противоположные, не связанные между собой практики. Но, в действительности, они представляют два физиологически возможных способа достижения одной цели — анормального соотношения активности левого и правого полушарий. В одном случае это осуществляется посредством волевого успокаивания, прекращения подпитки информацией левого полушария с одновременным нагружением правого, а в другом — посредством перегрузки левого полушария, вслед за чем рефлекторно наступает его запредельное торможение.
        Универсальный статус этих двух подходов иллюстрируется их распространением в различных культурных регионах, не имевших тесных контактов между собой, причем, некоторые культуры достигли поразительной проницательности в понимании механизмов действия соответствующих приемов. Так, среди мезо-американских индейцев [18] имеется четкое разделение двух форм мировосприятия, именуемых тонал и негуал, и существует система детально разработанных приемов (восходящих, как утверждает предание, к временам цивилизации тольтеков), назначение которых прямо объявляется как «перенасыщение информацией обычного взгляда на мир» и «выключение внутреннего диалога» с целью «коллапсирования тонала», иными словами — левополушарного доминирования.

        Перераспределение функций между полушариями наблюдалось нами и в экспериментах с Шри Янтрой (таблица 2), когда рассмотрение Шри Янтры для успокаиваемой категории испытуемых по сравнению с другими предъявляемыми изображениями вызывает значительно большую активацию правого полушария относительно левого (отношение 0.78). Можно предположить, что это свойство также играет существенную роль в медитационных ритуалах со Шри Янтрой.