CONAN-m

Metrological comparison of direct and spectral estimates of EEG amplitude in frequency domains
г A.P. Kulaichev, 2016
citing: International Journal of Psychological and Brain Sciences. 2016, 1(2):21-28.

Аннотация: This work performs the metrological comparison of two groups of indicators estimating the average level of EEG–potentials. The indirect spectral indicators (ISI) based on amplitude spectrum and power spectrum are contrasted with natural indicators (NI) based on period-amplitude analysis, on EEG absolute value and on EEG envelope. Five major results were obtained: 1) NI give almost equivalent estimates that differ from ISI significantly; 2) NI demonstrate smooth dynamics of their value change at successive epochs whereas ISI are subject to drastic and casual fluctuations; 3) ISI unlike NI do not possess the additivity property of statistical averaging, their estimates depending on number and length of averaged epochs can differ over 3 times in their values; 4) ISI at simulated signals with a known amplitude ratio give estimates that differ 1.4–1.55 times from true value whereas NI show the proper estimates; 5) ISI depending on differences between EEG spectral distribution give estimates which differ over 5 times in their ratios while NI show the same ratios which differ 1.38–3.7 times from ISI.
The least reliable results in all comparisons are related to the power spectrum. These conclusions do not allow to qualify metrologically ISI as an analytical tool that is adequate for the nature and peculiarities of EEG potentials. Their use may lead to incompatibility of the results obtained by different researchers.
Ключевые слова: EEG amplitude, amplitude spectrum, power spectrum, period-amplitude analysis, envelope, filtration, metrology

1. Introduction

     In this work we examine and discuss one of the major questions for the field of metrology. It is concerned with those criteria, estimates and standards in computing or quantitative EEG (QEEG) that were not generally formulated for a number of reasons (Kulaichev, 2007). As follows from the special monographic review (Tong, Thankor, 2009) as well as from many papers on QEEG, metrological questions still remain beyond the scope of interest of EEG researchers. The newly proposed mathematical methods are not compared with their previous analogues, their efficiency in solving typical physiological tasks is not estimated, compared, and neither it is statistically verified. The methods traditionally used in practice are not critically examined and reviewed. Moreover, there is still no global normative EEG database.
     Only a fraction of literature on the topic (Ivanov, 2011, Kulaichev, 2007, 2009, 2011, Orihovskaya, Antonova-Rafi, 2014) focuses on special metrological aspects. A separate branch is represented by 65 years long discussion about an optimal EEG reference which still has not led to the development of some universally estimated quantitative criteria and standards (cf. reviews in Ng., Raveendran, 2007, Kayser, Tenke, 2010). The lack of metrological support and standards leads to incompatibility and inconsistency of results and conclusions drawn by different researchers (cf. literature reviews in (Kulaichev, 2012, Kulaichev, Gorbachevskaya, 2013, Kulaichev, Iznak et al., 2014)).
     More favourable situation developed in traditional clinical EEG diagnostics which focused entirely on visual studying of records and where clear criteria and standards for both symptomatology and drawing clinical conclusions were formulated (Deuschl, Eisen, 1999). Another positive example is concerned with heart rate variability analysis where the permanent international working group established by European cardiological society and North American society of stimulation and electrophysiology several decades ago provides metrological standardization and regulation of computing methods and estimated indicators (Malik et al, 1996).
     One way or another, the scientific EEG investigations during many decades mainly followed the physical and technical applications of mathematical methods of signal analysis which were often directly and noncritically transferred by invited engineering specialists without any consideration given to fundamental nonstationarity of bio-signals and nonharmonic nature of their sources (Kulaichev, 2007). Indeed, there isn't any widely known pure or applied mathematician who developed special methods of EEG analysis.
     However, there will hardly be objections against the vital necessity to seek better accuracy and more adequate measurement as well as analytical tools in any field of science or domain of knowledge. If a researcher has two analytical tools with different measurement error then being responsible for the evidence and consultations he presents he will definitely choose the tool of higher measuring accuracy and reliability, otherwise scientific community can qualify his results and conclusions as insufficiently convincing. Furthermore, fundamental questions of accuracy and adequacy of measuring and analytical means are undoubtedly methodically significant, actual and primary in any scientific area including EEG studies.
    Based on the aforesaid, our aim is to compare metrologically the direct measurements of average EEG amplitude in frequency domains to indirect estimates obtained from amplitude and power spectra. The following analysis reveals the numerous errors peculiar to spectral EEG amplitude estimates.

2. Methods to estimate EEG average amplitude

     From the very beginning of the computer era, especially due to FFT algorithm developed in 1965, EEG amplitude in chosen frequency domain began to be estimated via amplitude spectrum or power spectrum as squared amplitude spectrum (Otnes, Enochson, 1978, Randall, 1987).
     However, in case of insufficient professional mathematical intuition a nonlinear relationship between power spectrum estimates is difficult to perceive in comparison with linear relationship between amplitude spectrum estimates. Moreover, it is not easy to realize the physiological meaning of estimations expressed in squared microvolts when EEG biopotentials are initially measured rather than their squares or volumes. As a result of its nonlinearity the power spectrum is characterized by dominant high-amplitude peaks with leveled and even disappearing medium-amplitude and low-amplitude details. This is expressed in ratios of frequency domains in chosen derivation and in ratios of derivations in chosen domain but it is visually-hypertrophied and evident for topographic maps displaying only two areas on a scalp in blue and red colours. And finally, let us speculate about the mathematical meaning of power spectrum average value. It is the dispersion of EEG amplitude spectrum with respect to zero as the mean value (Otnes, Enochson, 1978). The rhetorical question immediately arises: what physiological meaning can be associated with this indicator?
     Moreover, the results of spectral analysis are characterized by a number of errors, the most famous one is the power leakage from the main peaks. However this effect is narrowed by increased frequency resolution and it is accounted for signals with powerful monoharmonic sources. That does not correspond to EEG where this kind of generators does not exist. So if the phenomenon does not exist, any ways of dealing with it (Harris, 1978) make no sense. Less known error is caused by the influence of amplitude modulation which is inherent in EEG signals. It leads to appearance of side peaks in spectrum which can be at a considerable distance from the main peak (Kulaichev, 2007).
     Notably, at frequency resolution of 0.25 Hz and better distribution of EEG, spectral harmonics appears to be a chaotic sequence of high and low amplitude components which are also highly variable in their amplitude and frequency through epochs (fig.1). Therefore, separate harmonics are not viable for analysis and they make no physiological sense. And that is why the averaged spectral estimates within a selected frequency domain are commonly used in practice for they are more statistically stable indicators. These indicators will be considered as indirect estimates based on amplitude spectrum (As) and power spectrum (Ps).

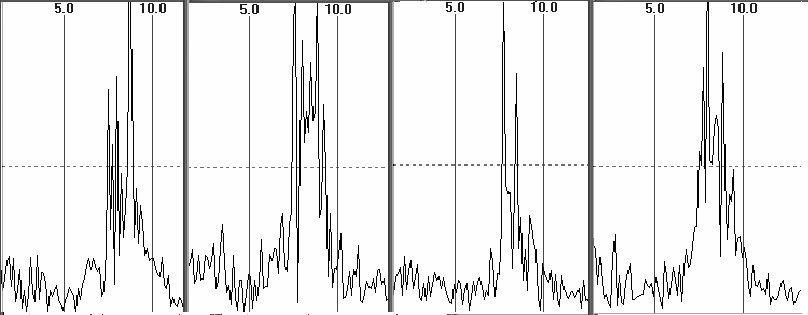
Fig.1. The amplitude spectra in four successive 8-second epochs in O2 derivation, "closed eyes" test

Now let us discuss what is meant by "average signal amplitude". For monoharmonic signals the answer seems to be obvious - it is the difference between maximum and minimum of oscillations. In case of polyharmonic character of signal the answer is not so obvious. During the pre-computer era this problem was solved by period-amplitude analysis when the measurements of amplitudes and periods of consecutive oscillations were performed manually on paper record, then the average amplitude was calculated (it is designated it as Ap), as well as other descriptive statistics. With the profound use of computers this method was fulfilled by a preliminary digital signal filtration in a chosen frequency domain and subsequent automatic measurements of differences between ascending and descending amplitude extremums (fig. 2B). Under these conditions, however, there are two options depending on a critical decision: to consider or not to consider the amplitude differences relating to periods which are beyond the analyzed frequency domain (such periods usually belong to the low-amplitude oscillations). Furthermore, averaging of amplitude differences usually is not corrected taking into account variability of their temporary duration.

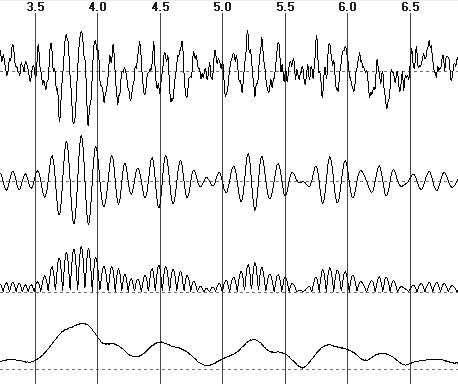
Fig.2. From top to bottom: the EEG fragment, its filtering in alpha domain, the module of filtered signal, the EEG envelope

Another method comparatively simple for application consists in calculating the mean of EEG absolute value (fig. 2C, this indicator is designated as Am). Indeed, as such measurements are preceded by EEG filtration in a frequency domain, then the transformed record is centered around zero and both positive and negative EEG extremums are quite symmetric and their dynamics are sufficiently smooth. Therefore, averaging of amplitudes of the signal through all time samples gives a stable and balanced measure of average EEG amplitude. As the simple calculations can show, this indicator also considers the temporal variability of EEG periods.
The third alternative estimation can be a mean value of EEG envelope (fig. 2D) which reflects the signal amplitude modulation (this indicator will be denoted as Ae). In this connection Ae is similar to 0.5 of Ap but it is disposed of quantization of EEG extremums in time and of variability of their periods.
These three indicators are referred below as “natural measures” of average EEG amplitude and they are compared with indirect spectral estimates.

3. Results
3.1. Integral differences

Here let us estimate distinctions between Ps, As, Ap, Am, Ae indicators using 32-seconds EEG record for "closed eyes" test, 10-20% system of derivations, 256 Hz sampling rate, and analysis in alpha domain. Since the values of indicators vary significantly then Z-normalization of values of each indicator throughout all derivations should be performed for comparability of results.
Fig. 3 shows the evaluation of Ps, As, Ae estimates through four derivation meridians (Ap and Am values by reason of their proximity to Ae are not shown). As it can be easily seen, this record demonstrates classical consecutive reduction of alpha rhythm amplitude from occipital to frontal derivations with noticeable left- and right-handed asymmetry in parietal and occipital areas. Furthermore, it is obvious a number of differences between three indicators changing their sign in some derivations.

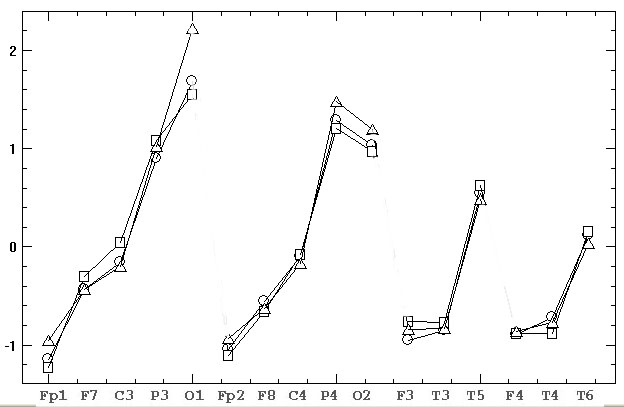
Fig.3. Z-normalized estimates of EEG average amplitude based on amplitude spectrum (squares), power spectrum (triangles) and EEG envelope (circles)

     First of all let us calculate descriptive statistics (variation range, mean ± standard deviation) for absolute values of differences of As, Ap, Am indicators relative to Ae:
|As-Ae|: 0.009–0.21,     0.101±0.058;
|Am-Ae|: 0.0001–0.012, 0.0036±0.003;
|Ap-Ae|: 0.0004–0.07,    0.003±0.002.
     The greater difference occurs for As, it reaches 21% of Z–value and its average difference exceeds 10%. The differences of Ap and Am from Ae are minimal, average difference does not exceed 0.36% of Z–value. The divergences between the mean values of |As-Ae| and |Am-Ae| as well as of |As-Ae| and |Ap-Ae| are verified by t–test with high confidence p=0.000007. Nevertheless, the difference between |Am-Ae| and |Ap-Ae| is not significant at p=0.46, thus Ap and Am indicators may be regarded as equivalent.
Let us calculate similar statistics for the differences of three natural indicators relative to As:
|Ae-As|: 0.009–0.21, 0.101±0.058;
|Am-As|: 0.019–0.26, 0.12±0.066;
|Ap-As|: 0.004–0.21, 0.102±0.033.
     The null hypothesis of pairwise differences between |Ae-As|, |Am-As|, |Ap-As| are accepted with high confidence p=0.95, 0.95, 0.96, thus these three natural indicators can be considered as equivalent.
     Finally, let us perform calculations for Ps relative to Ae and As:
|Ps-Ae|: 0.003–0.54, 0.115±0.126;
|Ps-As|: 0.02–0.67,   0.169±0.157.
     Thus, power spectrum gives estimates greater then above-considered ones with respect to their variation ranges and mean values as compared to amplitude spectrum and envelope indicators.
     Summary. Three natural indicators of EEG average amplitude practically do not differ and may be regarded as equivalent ones, but they are significantly different from the indirect estimates based on amplitude spectrum. Even greater differences with the other four parameters are valid for the power spectrum.

3.2. Differential differences

     Several methodological approaches can be applied for a more detailed numerical study of adequacy of considered indicators. As the equivalence of free natural estimates has been shown above then in further comparisons the measure based on an envelope will be mainly used.
     The idea of the first approach is as follows. If we divide a hole EEG record onto overlapping epochs with a small time shift between themselves, the dynamics of adequate indicator values through epochs should become sufficiently smooth.
     Now let us consider the occipital O2 derivation with a high amplitude of alpha rhythm and the frontal F3 derivation with a low representation of alpha rhythm. Total 32-seconds time interval will be divided onto 150th epochs of 2-seconds duration and shifted at 0.2-seconds between themselves. For each i–th epoch (i=1-150) let us calculate As_i and Ae_i estimates. To make their comparison possible Z–normalization of each indicator should be performed for all epochs. Since the time shift between epochs amounts to 10% of their duration, temporal dynamics of adequate estimates through epochs should be sufficiently smooth without sharp fluctuations.
     Significant differences between the time dynamics of two indicators is illustrated in Fig.4: the dynamics for Ae is smoother compared to a high-amplitude random fluctuations for As. Besides, comparing O2 and F3 graphs reveals a whole series of episodes of opposite tendencies between two indexes, i.e. differences in their topographical relations. For example As_i and Ae_i estimates differ significantly in O2, but they are equal or their ratio changes to opposite in F3. Such topographic differences are extremely disturbing because they can lead to incompatibility of results and conclusions for intergroup comparisons estimating influence of various factors such as age, sex, occupation, pathology, functional condition, motivation, social or professional affiliation, etc.

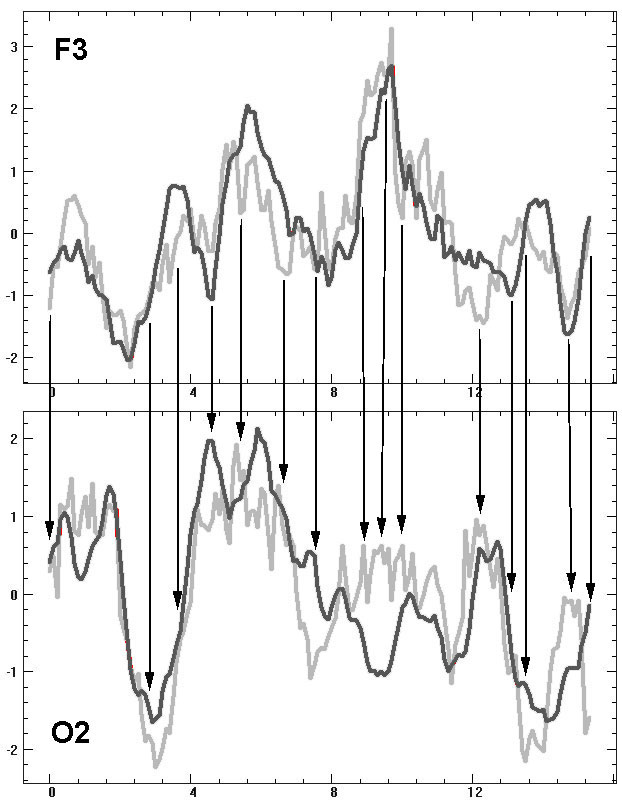
Fig. 4. Dynamics of average EEG amplitude in alpha domain at 150th 2-seconds epochs (x-axis) shifted by 0.2-seconds among themselves for F3 and O2 derivation, gray – amplitude spectrum estimates, black – EEG envelope estimates, the arrows mark the obvious episodes of topographical distinctions

The numerical estimation of the degree of "smoothness” of dynamics can be made if to calculate absolute differences for each X-indicator between pairs of subsequent epochs DX_i=|X_i+1-X_i| (i.e. absolute derivative) and then evaluate the mean value DX. The results of the quantitative comparison are given in the table 1 the columns of which include derivation, frequency domain, As or Ae indicator, mean absolute difference between As and Ae (i.e. mean values of |As_i-Ae_i|) with its standard deviation, mean value DAs or DAe (i.e. absolute derivative) with its standard deviation, a significance level of null-hypothesis “no distinction between DAs and DAe”.

Table 1. The results of the analysis of differential distinctions between average EEG amplitude estimates based on amplitude spectrum and EEG envelope

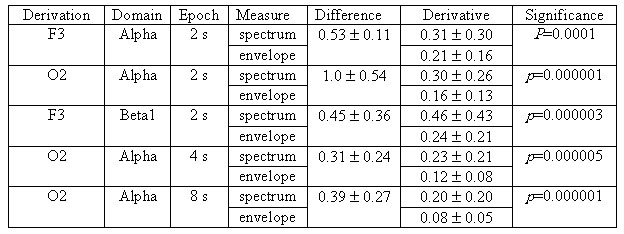     As anyone can see from the table.1 the average absolute difference between As_i and Ae_i is up to 31–100% of Z–value that much more exceeds the differences mentioned in the previous section. This situation is quite alarming because any researcher due to random factors can perform EEG recording in an error-prone time period.
     The mean values and standard deviations for DAe are 1.5–2 times smaller compared to DAs and the differences between DAe and DAs are highly significant statistically. Similar conclusions are also reproduced for higher frequency beta1-domain and for longer 4- and 8-seconds epochs. Thus, the revealed regularities are stable and reproducible regardless of derivation, frequency domain and epoch duration.
     Finally, let us asses the power spectrum estimates for alpha domain in O2 derivation and 2-seconds epoch. The average absolute differences between Ps and Ae are characterized by statistics 0.54±0.45 and between Ps and As by statistics 0.29±0.25. Statistics for DPs derivative is 0.25±0.21. It is significantly different from DAe at p=0.0001 and differs from DAs at p=0.02 by a statistical trend.
     Summary. The natural estimates of average EEG amplitude provide a smoother dynamics of their changes during neighbouring epochs whereas the spectral amplitude and power estimates are the subject to sharp and casual fluctuations. Furthermore, they do not coincide with each other by a statistical trend.

3.3. Additivity of averaging results

The statistical averaging operation has the property of additivity, namely: the mean value of the sample is equal to averaging of averaged values of its consistent subsamples. Natural estimates of EEG average amplitude possess those properties by definition.
Let us examine this property for spectral estimates. Let us take the same F3 and O2 derivations in alpha and beta1 domains and calculate As and Ps at 32-seconds epoch. Then this interval is divided into 2, 4, 8 epochs, calculate As_i and Ps_i at each i-epoch and average those estimates. The results are given in the table 2 which implies a consistent increase in As and Ps estimates depending on the number and size of epochs.

Table 2. Alterations of average EEG amplitude estimates based on amplitude and power spectrum depending on the number and size of averaged epochs

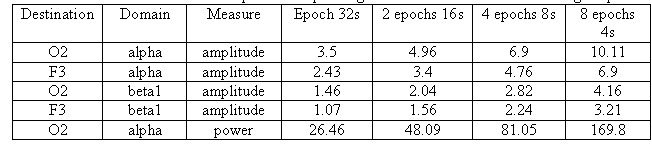This situation is also quite alarming because different researchers analyze EEG records of different lengths, so their results and conclusions may be incomparable and even contradictory in some cases. This property is not inherent to a particular frequency characteristic (amplitude spectrum, power spectrum, etc.) but to FFT method itself applied for EEG signals. By increasing the analysis period and frequency resolution in EEG spectra more harmonics with low amplitude appear and such harmonics make no physiological sense. It results in the systematic reduction of average values with increasing of epoch length according to the law very close to the linear one (table. 2).
Summary. The indirect spectral estimates of average EEG amplitude do not possess the property of additivity of statistical averaging operations. The resulting estimates depending on the number and length of averaged epochs can differ over 3 times in their values.

3.4. Comparison on simulated signals

Now let us compare natural and indirect estimates of average EEG amplitude using two synthesized signals (fig. 5).

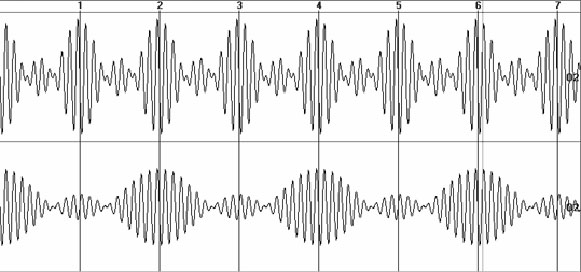
Fig. 5. Two synthesized signals of 32-seconds length: 1) the sum of 3 harmonics of 184 µV amplitude and 9, 10, 11 Hz frequencies; 2) the sum of 3 harmonics of 122 µV amplitude and 9.5, 10, 10.5 Hz frequencies

As anyone can see, the ratio of the original harmonic amplitudes is 184/122=1.508. The similar ratio is for means of variations range of synthesized signals: (548.3+19.2)/2=283.8 µV, (367.4+6.3)/2=186.8 µV, the ratio is 1.512. It is obvious that an adequate measure should give the same ratio of two estimates:
As gives 8.64 and 4.1 µV, ratio=2.11
Ps: gives 492.2 and 220.2 µV2, ratio=2.34,
Ap gives 249.5 and 168.1 µV, ratio=1.48,
Am gives 83.1 and 55.5 µV, ratio=1.5;
Ae gives 88.04 and 132.1 µV, ratio=1.5.
Summary. The indirect spectral indicators of EEG average amplitude on simulated signals with known amplitude ratio produce estimates 2.11/1.511=1.4 and 2.34/1.511=1.55 times different from the correct values, whereas the natural indicators show correct ratio of mean amplitude of signals.

3.5. Dependence on spectral distribution

As it has been shown above, the natural indicators give correct amplitude estimation for known model signals. Therefore, they can be used them as a reference point to continue the comparison on real EEG records varying in the shape of distribution of spectral harmonic amplitudes (fig. 6).

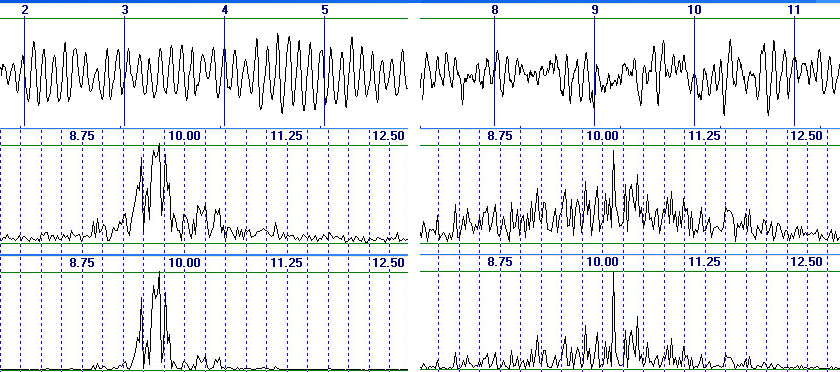
Fig.6. Two subjects with different spectral distribution in alpha domain, from top to bottom: EEG in O2 derivation, amplitude spectrum, power spectrumFig.6. Two subjects with different spectral distribution in alpha domain, from top to bottom: EEG in O2 derivation, amplitude spectrum, power spectrum

     As anyone can see, two examiners differ considerably in their EEG spectral distribution. For the first of them the frequency range of predominant alpha rhythm amplitudes is quite narrow 9.2–10 Hz, while for the second the range is wider 8-12 Hz. The resulting estimates are:
Ae: 31.3 and 118 µV, ratio=0.26;
Am: 20 and 75.3 µV, ratio=0.267;
Ap: 227.1 and 60.4 µV, ratio=0.266;
As: 4.1 and 11.29 µV, ratio=0.36;
Ps: 25 and 351.3 µV2, ratio=0.07.
     Note that the latest result would be a consequence of Ps quadratic suppression of harmonics on the lateral frequencies of the first examiner.
     Thus, the natural indicators demonstrate almost the same proportion (the difference between them is 0.267–0.26=0.007 or 0.007/0.26=2.7% of ratio value) while the spectral estimations 0.36/0.26=1.38 and 0.26/0.07=3.7 times differ from the natural ones according to their ratios respectively. In addition, the spectral indicators demonstrate even a greater difference between the ratio values (0.36/0.07=5.1 times). So as compared to correct natural indicators, As estimations for two examiners are closer between themselves whereas Ps estimations diverge considerably. This situation is rather disturbing since for intergroup comparisons it can lead to displacement of mean values and standard deviations. This may prevent statistically reliable detection of real differences or lead to identification of pseudo-differences.
     Summary. As and Ps indicators depending on differences between subjective EEG spectral distribution give estimates which differ over 5 times in their ratios while the natural indicators show the same relation of values 1.38–3.7 times different from spectral estimates ratios.

4. Conclusion

As it follows from the findings in sections 3.1-3.5, the spectral estimates of average EEG amplitude in frequency domains possess a number of significant and fundamental errors. In addition, the measures based on amplitude and power spectra differ in their estimates. These results and findings do not allow to qualify metrologically the spectral estimates as a viable (reliable) analytical tool adequate to the nature and specificity of EEG potentials. Their use may lead to inconsistency and thus incompatibility of results obtained by different researchers Therefore applying the natural estimates of average EEG amplitude seems to be more preferable and sustainable.

References

     Deuschl G., Eisen A. (1999). Recommendation for the practice of clinical neurophysiology: Guidelines of the International Federation of clinical neurophysiology. Elsevier, Amsterdam, 304 pp.
     Harris F.J. (1978) On the use of windows for harmonic analysis with the discrete Fourier transform. IEEE proceedings. (66)1:51–83.
     Ivanov L.B. (2011) On informativeness of use of coherent analysis in clinical electro-encephalography. Zh Vyssh Nerv Deiat Im I P Pavlova. 61(4): 499–512.
     Malik M., BiggerJ. T., Camm A.J., Kleiger R.E., Malliani A., Moss A.J., Schwartz. P.J. (1996) Heart rate variability. Standards of measurement, physiological interpretation, and clinical use. Eur Heart J. 17 (3): 354–381.
     Kayser J., Tenke C.E. (2010) In search of the Rosetta Stone for scalp EEG: Converging on reference–free techniques. Clin.Neurophysiol. 121:1973–1975.
     Kulaichev A.P. (2007) Computer electrophysiology and functional diagnostics, 4th edition. INFRA?M, Moscow, 640 pp.
     Kulaichev A.P. (2009) The informativeness of coherence analysis in EEG studies. Neurosci Behav Physiol . 59(6): 757–767.
     Kulaichev A.P. (2011) The method of correlation analysis of EEG synchronism and its possibilities. Zh Vyssh Nerv Deiat Im I P Pavlova. 61(4): 485–498.
     Kulaichev A.P. (2012) Comparative analysis of EEG correlation synchronism and EEG amplitude relationships in all-night sleep. Zh Vyssh Nerv Deiat Im I P Pavlova. 62(1): 108–119.
     Kulaichev A.P., Gorbachevskaya N.L. (2013) Differentiation of norm and disorders of schizophrenic spectrum by analysis of EEG correlation synchrony. J.Exp.Integr.Med. 3(4):267–278.
     Kulaichev A.P., Iznak A.F., Iznak E., Kornilov V.V., Sorokin S.A. (2014) The Changes of EEG correlation synchrony at depressive deviations of advanced age. Zh Vyssh Nerv Deiat Im I P Pavlova. 64(2):1–9.
     Ng S.C., Raveendran P. (2007) Comparison of different montages on to EEG classification. Biomed 06, IFMBE Proceedings 15, 365–368.
     Orihovskaya K.B., Antonova-Rafi U.V. (2014) The effect of EEG spectrum leakage when using Barletta filter and at his absence. Int research J. (22) 3–2: 42–43.
     Otnes R.K., Enochson L. (1987) Applied time series analisys, vol.1: bsaic techniques. N.Y. 1978. 428 pp.
     Randall R.B. (1987) Frequency Analysis, 3rd edition. Bruel & Kjaer, 344 рp.
     Tong S., Thankor N.V. (2009) Quantitative EEG analysis methods and clinical applications. Artech House, 421 pp.