
Лекция: Методы вычислительного
анализа ЭЭГ
г А.П.
Кулаичев. Компьютерная электрофизиология и функциональная диагностика.
Изд. 4-е, перераб. и доп. - М.: ИНФРА-М, 2007, с.178-230

Основные разделы анализа
ЭЭГ. При анализе ЭЭГ используются наиболее сложные в вычислительном
отношении спектрально-аналитические методы. Поэтому для овладения ими требуется
повышенная сосредоточенность, усилие и привлечение знаний из школьной математики.
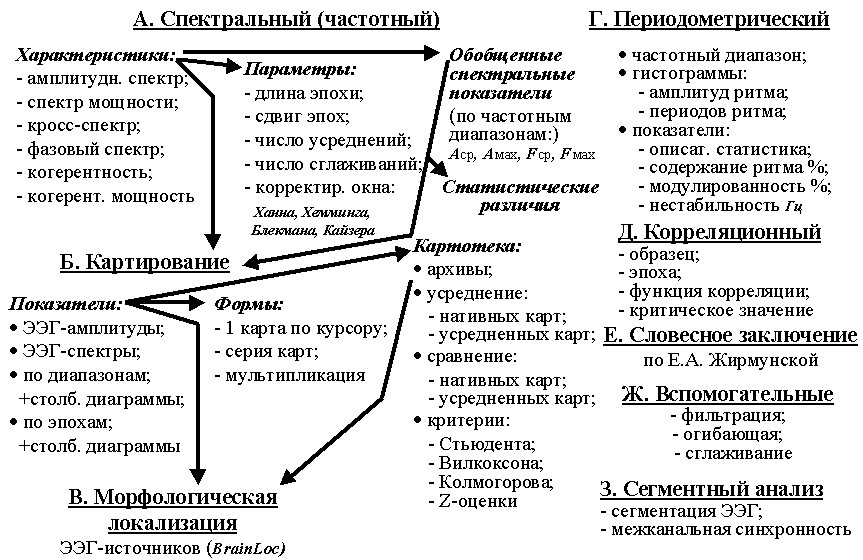
Рис. 4.13. Методы вычислительного анализа ЭЭГ
В дидактическом плане встает ряд закономерных
вопросов: а) какие методы используются многими исследователями, а какие
имеют локальный или поисковый характер? б) взаимосвязаны ли между собой
и как именно различные методы? и так далее.
Сначала мы лишь кратко терминологически промаркируем
данную схему с последующим более подробным рассмотрением методов.
Наиболее объемный, разветвленный и важный подраздел
составляют методы частотного или спектрального анализа и связанные с ним
подразделы. Эти методы были созданы для исследования сигналов или процессов
физического и технического происхождения и лишь значительно позже они начали
использоваться в области электрофизиологии. На первом этапе по ЭЭГ-сигналу
могут быть вычислены различные частотные характеристики (представляющие
собой зависимость конкретного спектрального показателя от частоты): амплитудный
спектр, спектр мощности, фазовый спектр, кросс-спектр, когерентность, когерентная
мощность и другие. Вычисление этих характеристик регулируют ряд установочных
(задаваемых) параметров: длина эпохи анализа и сдвиг эпох (вся запись ЭЭГ
может быть разбита на несколько эпох с заданным сдвигом относительно друг
друга), число усреднений и сглаживаний спектра, корректирующие окна (для
уменьшения эффекта вытекания мощности). По каждой такой частотной характеристике
могут быть вычислены обобщенные спектральные показатели в заданных диапазонах
частот (например, в стандартных диапазонах: дельта, тета, альфа, бета)
и по ним оценены статистические различия спектров (между парами одноименных
отведений двух записей или между всеми парами отведений одной записи).
Затем различные ЭЭГ-показатели по всему набору
зарегистрированных отведений могут выступать исходным материалом для топографического
картирования — наглядного представления распределения значений выбранного
показателя на скальпе в многоцветной шкале. Картироваться могут: амплитуды
ЭЭГ для заданного момента времени, спектральные показатели для заданной
частоты, обобщенные спектральные показатели (ОСП) в заданном частотном
диапазоне. Картирование ОСП может производиться по частотным диапазонам
в рамках текущей эпохи анализа или в выбранном диапазоне по эпохам, на
которые разбита ЭЭГ-запись. Такое картирование может сопровождаться столбиковыми
диаграммами изменения ЭЭГ-показателя по всем отведениям. Визуализация карт
может осуществляться в трех формах: одна карта, управляемая подвижным визиром
(перемещаемым по времени, частоте, диапазону, эпохе); серия карт (для некоторого
интервала времени, частот, диапазонов, эпох); анимированная серия карт
(мультипликация).
Далее, любые карты могут быть сохранены и усреднены
в картотеке. Усреднение может проводиться дифференцированно для различных
физиологических состояний, проб, заболеваний и т. п. Содержимое картотеки
представляет интерес для статистической оценки попарных различий между
картами: между двумя нативными, между нативной и усредненной или между
усредненными.
И наконец, любой из рассмотренных показателей
может быть использован для трехмерной локализации ЭЭГ-источников в анатомических
структурах головного мозга.
Следующий самостоятельный подраздел составляет
периодометрический анализ ЭЭГ. Хотя этот метод возник и широко применялся
еще до внедрения методов спектрального анализа, однако он позволяет более
детально исследовать распределения амплитуд и частот ритмов в заданном
частотном диапазоне с построением гистограмм, вычислением показателей описательной
статистики, процента содержания и модулированности ритма, его частотной
нестабильности.
К подразделам дополнительного и вспомогательного
характера можно отнести следующие:
корреляционный анализ с вычислением авто- и кросс-корреляционных
функций (по заданному образцу и на заданной эпохе) со статистической оценкой
значимости корреляций по критическому значению;
словесное заключение по отклонениям от нормы с использованием
алгоритма нормопатологической классификации Е.А. Жирмунской;
математические преобразования ЭЭГ — фильтрация, вычисление
огибающей, сглаживание и др.
сегментный анализ, связанный с маркированием участков
стационар-ности ЭЭГ, оценкой межсегментной синхронности и классификацией
доминирующих топографических паттернов.
Рассмотрим перечисленные методы подробнее, начав
с математических аспектов частотного (спектрального) анализа ЭЭГ, как наиболее
сложного и многообразного.
Спектральный анализ ЭЭГ
Преобразование Фурье.
Математической основой частотного анализа является преобразование Фурье
(французский
математик Жан Батист Жозеф Фурье сформулировал это преобразование в 1822
г.), принимающее различные формы в зависимости от вида анализируемых
сигналов. Однако общим является предположение о том, что исследуемые процессы
(сигналы) состоят из определенного числа (возможно бесконечного) синусоидальных
и/или косинусоидальных составляющих (гармоник) последовательно возрастающего
ряда частот.
Преобразование Фурье и осуществляет разложение
сигнала на ряд гармонических составляющих без какой-либо потери информации
(если арифметически сложить все гармоники, то получится опять исходный
сигнал). Каждая гармоника определяется тремя параметрами: амплитудой, начальной
фазой и частотой. Зависимость амплитуды и фазы гармоник от частоты называется
спектром.
В случае непрерывного и бесконечного по длительности
сигнала его спектр также будет непрерывным и бесконечным в частотной области.
На практике же мы имеем дело с ограниченными во времени сигналами, амплитуды
которых измерены через равные промежутки времени (дискретизованы тактами
АЦП). Поэтому и результирующий спектр получается тоже дискретным и ограниченным
в частотной области (состоящим из отдельных спектральных линий). Такое
разложение дает модификация метода, называемая дискретным преобразованием
Фурье.
В большинстве источников математические аспекты
частотного анализа формулируются в обобщенном интегральном виде. Такая
форма представления материала крайне затрудняет понимание его сущности,
а ручная проверка справедливости отдельных формул и их прямая алгоритмическая
реализация часто не представляются возможными. Вместе с тем кажущиеся сложными
математические вопросы можно изложить намного проще, доступнее и нагляднее
с использованием тригонометрического и графического представлений.
Из школьной математики.
Гармоническое колебание заданной амплитуды А и периода Т
может быть получено посредством вращения вектора длиной А с частотой
f=1/T
в фазовой плоскости (рис. 4.14, а). Во временной развертке изменение проекции
вектора на ось ординат будет иметь вид синусоидально-косинусоидального
процесса (рис. 4.14, б).
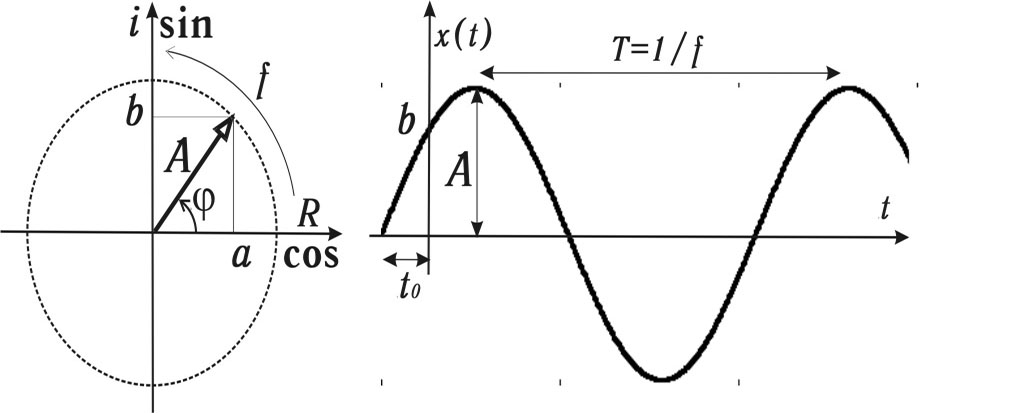
а)
б)
Рис. 4.14. Представление гармонического процесса:
а — фазовая плоскость; б — временная
развертка
Мы начинаем наблюдение за процессом в некоторый произвольный
момент времени t=0, что соответствует положению вектора на фазовой
плоскости с углом 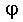 . Поэтому амплитуда
процесса в любой момент времени t будет определяться выражением
. Поэтому амплитуда
процесса в любой момент времени t будет определяться выражением 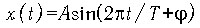 или, выражая период
T через частоту f,
или, выражая период
T через частоту f, 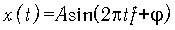 .
Отметим, что начальная фаза
.
Отметим, что начальная фаза 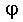 во временной развертке выражается через время
во временной развертке выражается через время 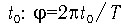 .
.
Введем обозначение 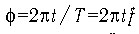 для текущего углового фазового сдвига
для текущего углового фазового сдвига 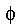 относительно начальной фазы
относительно начальной фазы 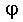 ,
тогда выражение для гармоники упростится:
,
тогда выражение для гармоники упростится: 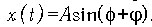 .
Используя разложение синуса суммы двух углов, эту формулу можно преобразовать
к виду:
.
Используя разложение синуса суммы двух углов, эту формулу можно преобразовать
к виду: 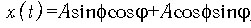 , а переходя к начальным
проекциям a и b вектора A на фазовой плоскости (рис.
4.14, а):
, а переходя к начальным
проекциям a и b вектора A на фазовой плоскости (рис.
4.14, а): 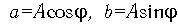 , получим выражение:
, получим выражение: 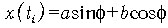 .
Таким образом, гармонику можно представить в виде суммы синуса и косинуса
с амплитудами a и b. Действительно, из рисунка фазовой плоскости
следует, что вращение вектора A эквивалентно сумме вращений его начальных
проекций a и b, при этом амплитуда A и фаза
.
Таким образом, гармонику можно представить в виде суммы синуса и косинуса
с амплитудами a и b. Действительно, из рисунка фазовой плоскости
следует, что вращение вектора A эквивалентно сумме вращений его начальных
проекций a и b, при этом амплитуда A и фаза 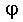 гармоники выражается через эти проекции простыми формулами:
гармоники выражается через эти проекции простыми формулами: 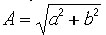 ,
, 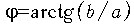 .
.
Исходя из приведенных соотношений, оси абсцисс
и ординат на фазовой плоскости часто называют осями косинуса и синуса или
же трактуют как действительную R и мнимую i оси, при этом
умножение вектора на мнимую единицу i означает его фазовый поворот
на 90°.
Дискретное
преобразование Фурье (ДПФ) осуществляет разложение сигнала x(t),
дискретизованного с частотой оцифровки
F и ограниченного во времени
на интервале наблюдения T, также в дискретизованный и ограниченный
по диапазону частот ряд n гармонических составляющих — спектр (рис.
4.15).
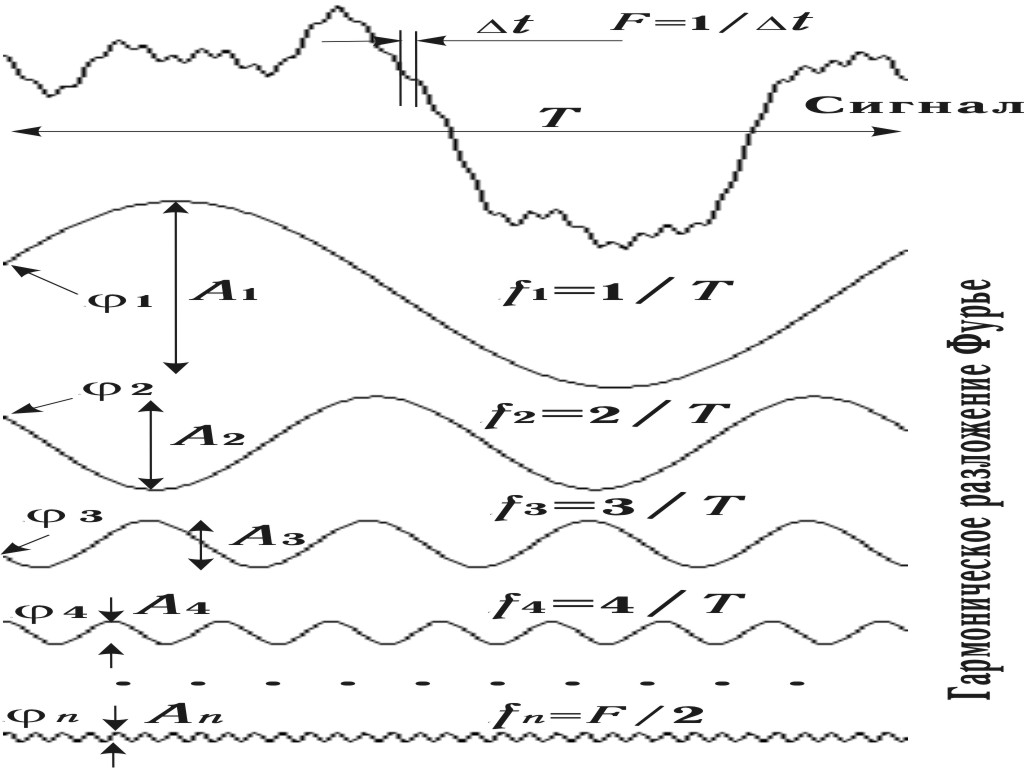
Рис. 4.15. Разложение сигнала в гармонический ряд
Фурье
|
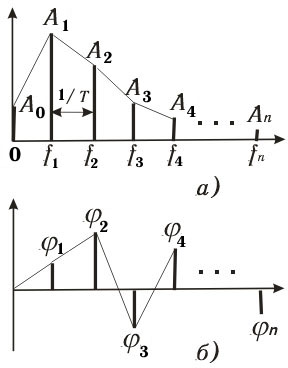
Рис. 4.16. Частотные характеристики:
а — амплитудная; б — фазовая
|
В результате получается так называемый образ X(f) в частотной
области для праобраза x(t) во временной области
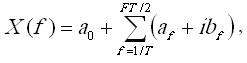 (4.1)
где a0 — постоянная составляющая, среднее значение
сигнала;
(4.1)
где a0 — постоянная составляющая, среднее значение
сигнала;
af, bf
— начальные амплитуды синусоидальной и косинусоидальной компонент f-ой
гармоники;
i — мнимая единица.
Амплитуда и фаза f-ой спектральной гармоники,
как мы видели выше, выражаются через амплитуды синусоидальной и косинусоидальной
компонент:
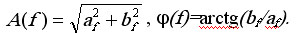 (4.2)
Тем самым результат ДПФ может быть исчерпывающе представлен
двумя частотными характеристиками (рис. 4.16) — зависимостями амплитуд
A(f)
и фаз ф(f) спектральных гармоник от частоты. Результат ДПФ сохраняет
всю информацию об исходном процессе x(t) и обладает важным свойством
обратимости: если к X(f) повторно применить ДПФ, то будет восстановлен
исходный сигнал x(t). Такая операция называется обратным Фурье-преобразованием.
Это свойство можно продемонстрировать на рис. 4.15 – если для любого временного
отсчета сложить амплитуды всех гармоник, то получим амплитуду исходного
сигнала в этой точке.
(4.2)
Тем самым результат ДПФ может быть исчерпывающе представлен
двумя частотными характеристиками (рис. 4.16) — зависимостями амплитуд
A(f)
и фаз ф(f) спектральных гармоник от частоты. Результат ДПФ сохраняет
всю информацию об исходном процессе x(t) и обладает важным свойством
обратимости: если к X(f) повторно применить ДПФ, то будет восстановлен
исходный сигнал x(t). Такая операция называется обратным Фурье-преобразованием.
Это свойство можно продемонстрировать на рис. 4.15 – если для любого временного
отсчета сложить амплитуды всех гармоник, то получим амплитуду исходного
сигнала в этой точке.
В чисто вычислительном плане результат ДПФ состоит
в следующем. На эпохе Т мы имеем N отсчетов амплитуды сигнала
x(t),
выполненных с дискретизацией Dt, иными словами
имеется вектор-массив из N значений. В результате ДПФ получается
новый вектор-массив из N значений, состоящий из двух частей длиной
N/2,
эти две части содержат амплитуды гармоник af и
bf
. Повторное применение ДПФ к данному массиву восстанавливает исходный сигнал.
Оценочные показатели ДПФ
Результат ДПФ характеризуется несколькими показателями.
Разрешение по частоте.
Частотная дискретизация спектра Df=1/T
является важным показателем ДПФ, называемым разрешением по частоте. Он
показывает, насколько детально представлен частотный спектр гармонических
составляющих сигнала, насколько близко расположены спектральные линии (ср.
рис. 4.21а,б).
Первая же из выделяемых гармоник имеет период,
равный эпохе анализа, поскольку для более низкочастотных гармоник нет возможности
достоверно оценить их амплитуду.
Частота Найквиста.
Последняя гармоника, которую можно выделить из сигнала (самая высокочастотная),
имеет частоту F/2, где F — частота дискретизации сигнала
соответственно установленному временному шагу Dt
работы АЦП. Эта частота называется частотой Найквиста. Об этом частотном
пределе говорят несколько математических теорем разных авторов в разных
технических областях (в частности, теорема Котельникова). Но пояснение
может быть более простым. Чтобы как-то зарегистрировать гармонику и оценить
ее амплитуду, мы должны произвести не менее двух измерений на каждом из
ее периодов (рис. 4.17). То есть частота измерений должна быть не менее
чем вдвое выше частоты гармоники.
Ширина полосы.
Таким образом, выделяемый из сигнала для последующего анализа частотный
диапазон гармонических составляющих простирается от 1/T до F/2
и является вторым важным показателем ДПФ, называемым шириной полосы. Общее
же число выделенных гармоник n равно отношению верхней частоты fn
к шагу частотной дискретизации Df, т.
е.: n=FT/2=N/2, где N — в число отсчетов амплитуды,
зарегистрированных на интервале наблюдения Т.
Точность оценки амплитуды
спектра возрастает от крайних гармоник к центральным (отметим,
что в литературе этим аспектам по непонятным причинам не уделяется внимание).
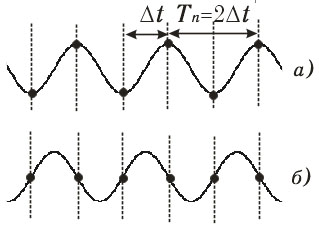
Рис. 4.17. Оценка амплитуды гармоники F/2:
а — точное значение; б — нулевое значение
Рассмотрим сначала высокочастотную гармонику F/2,
период которой в 2 раза длиннее интервала дискретизации. По случайным причинам
сдвига фазы гармоники относительно начала измерений мы можем иметь два
крайних варианта (рис. 4.17): можно попадать измерениями всегда в максимумы
и минимумы гармоники или — всегда в точки средних значений. В первом случае
мы получим точную оценку амплитуды гармоники, а во втором случае — нулевое
значение амплитуды. Все остальное множество вариантов начального сдвига
фазы будет покрывать область промежуточных точностей между этими граничными
случаями. При переходе к более длиннопериодическим гармоникам будет все
большее число измерений на каждом периоде и все большая вероятность точной
оценки амплитуды гармоники.
Посмотрим, что же делается на другом низкочастотном
краю 1/T. Там имеем только один наблюденный период гармоники. Но
эта гармоника вполне может быть модулирована по амплитуде составляющей
сверхнизкой частоты (подобно альфа-веретенам, рис. 4.18, б). Тогда своим
наблюдением мы можем случайно попасть как в период максимума модуляции,
так и в период минимума (имея в виду, что наш интервал наблюдения составляет
менее 1/4 временного диапазона на рис. 4.18, б). При увеличении же частоты
гармоники мы наблюдаем все больше ее периодов и все менее становимся зависимы
от эффектов сверхнизкочастотной модуляции.
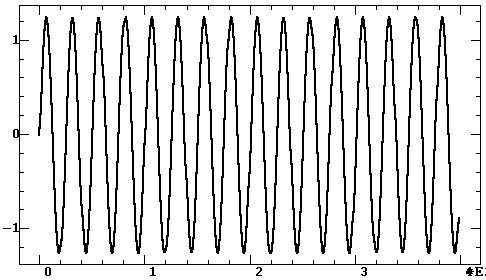
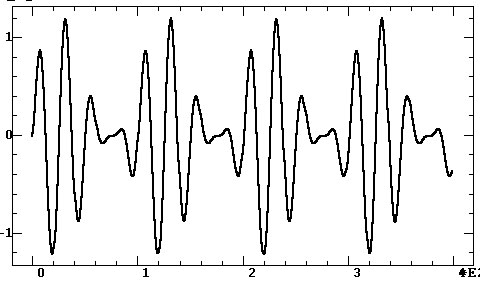
а)
б)
в)
г)
Рис. 4.18. Влияние амплитудной модуляции:
а, б — моногармонический и модулированный сигналы;
в,
г — их амплитудные спектры
Планирование исследования.
Естественным желанием исследователя является расширение частотной полосы,
увеличение разрешения по частоте и повышение точности измерения амплитуды
гармоник в интересующим его диапазоне частот. Увеличение верхней границы
полосы может быть достигнуто повышением частоты дискретизации F.
Для увеличения точности вычисления амплитуд верхних гармоник желательно
иметь 30-40%-ный запас. Поскольку обычно исследователя интересуют гармоники
ЭЭГ до 32 Гц (диапазон бета-2), то достаточно использовать F=2*32*1,4=89,6
Гц. Поэтому типовые частоты дискретизации ЭЭГ в 100 и 128 Гц вполне обеспечивают
необходимый запас точности. Сдвиг же полосы в низкочастотную область и
увеличение разрешения по частоте возможно лишь за счет увеличения интервала
наблюдения Т, а это невозможно при необходимости анализа изменения
ЭЭГ на кратковременных отрезках.
Модификации ДПФ
Быстрое преобразование Фурье
(БПФ, FFT). Алгоритм БПФ является одним из вариантов ДПФ, позволяющим
получить результат с минимумом простых арифметических операций. Со времени
своего первого опубликования в 1965 г. он произвел коренной переворот в
анализе сигналов на базе компьютерных и микропроцессорных систем.
Наиболее эффективен вариант алгоритм БПФ по основанию
2 (в этом случае исходная матрица решаемого уравнения размером
N
разлагается на log2N
индивидуальных
матриц, благодаря чему число необходимых операций умножения уменьшается
с N2 до N*log2N)
. Впоследствии была найдена еще более быстрая модификация этого алгоритма
— преобразование Хартли. При применении этих алгоритмов анализируемая эпоха
должна быть кратна степени 2, т. е. включать 256, 512, 1024, 2048, 4096
и т. д. дискретных отсчетов сигнала. С другой стороны, чтобы такие эпохи
выражались во временном измерении в целых числах и результаты в частотном
измерении тоже выражались в целых числах, желательно частоту регистрации
сигналов также устанавливать кратной степени числа 2
Некоторые дополнительные аспекты применения БПФ,
связанные с целочисленной арифметикой, увеличением масштаба частоты и быстродействием,
рассмотрены в [44].
Погрешности ДПФ
Вытекание мощности.
Эффект вытекания мощности или утечка выражается в уменьшении амплитуды
высоких спектральных пиков и появлении у них ложных боковых составляющих
постепенно уменьшающейся амплитуды. Непонимание этого явления может привести
ко многим неприятностям и научным казусам подобно открытию взаимосвязи
между амплитудами альфа и бета активностью ЭЭГ (этот пример подробно рассмотрен
в [38, 43]).
Для объяснения механизма возникновения эффекта утечки
в математических работах [13, 17, 20] используются различные малопонятные
нематематической аудитории термины: наложение прямоугольного окна, разрывы
сигнала на концах, явление Гиббса, боковые лепестки и др. Однако возможно
намного более простое, понятное и наглядное объяснение данного явления.
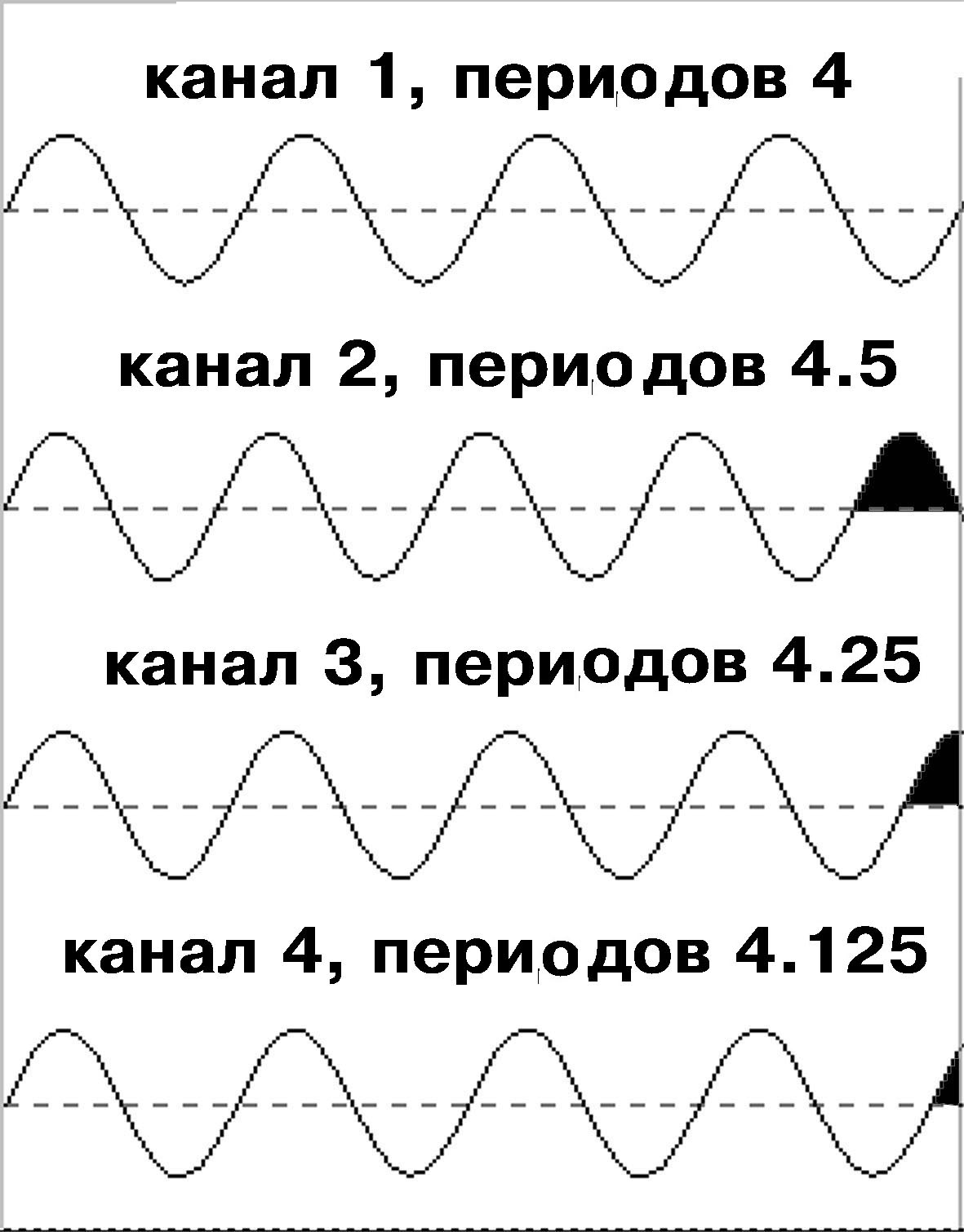
Возьмем некоторую, пока неизвестную гармонику
с частотой fi, реально существующую в зарегистрированном
сигнале ЭЭГ. Все дело состоит в том, насколько хорошо эта гармоника укладывается
своим периодом Ti=1/fi в интервал наблюдения
Т.
Если гармоника укладывается на Т точно целым числом своих периодов,
то она однозначно выделяется алгоритмом ДПФ, попадая точно в имеющуюся
спектральную линию с порядковым номером Т/Ti (напомним,
что эти линии следуют с дискретизаций 1/Т). Амплитуда гармоники
вычисляется точно, никакого эффекта утечки нет и на АЧХ наблюдается единственный
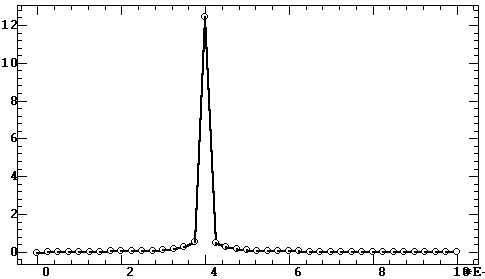
пик на частоте fi. На рис. 4.19, а на канале 1
представлена именно такая гармоника. В результате спектрального анализа
(рис. 4.25, б) на этом канале мы имеем единственный пик и его амплитуда
равна истинному значению амплитуды гармоники.
Если же гармоника укладывается на Т точно
полуцелым числом своих периодов, то она попадает в середину между двумя
спектральными линиями и не может быть представлена в спектре одной гармоникой.
Алгоритм ДПФ, как обычно, осуществляет разложение этого «сложного» сигнала
на сумму гармонических составляющих. И соседние спектральные линии получают
свои, все уменьшающиеся «куски» от истинной амплитуды такой гармоники —
возникает утечка мощности из спектрального пика. Пример такой гармоники
с полуцелым числом периодов на эпохе анализа приведен на рис. 4.25, а
на канале 2. В спектре (рис. 4.19, б) мы наблюдаем широкую размытость
пика со значительным снижением его амплитуды.
а)
б)
в)
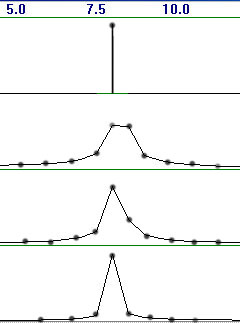
Рис. 4.19. Эффект утечки:
а — четыре моногармонических сигнала с разным
числом периодов на эпохе анализа; б — спектральные пики; в
— спектры с коррекцией окном Ханна
При множестве промежуточных вариантов между этими
двумя крайними случаями утечка также может варьироваться от максимальной
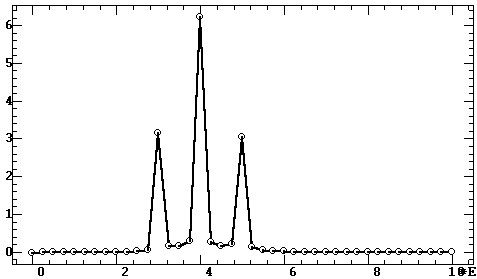
до минимальной. Примеры этому на рис. 4.19, а являют гармоники по
каналам 3, 4, частоты которых все более приближаются к левой спектральной
линии. В спектре (рис. 4.19, б) для этих гармоник мы наблюдаем все
меньшую размытость пика с увеличением его амплитуды (максимальные амплитуды
спектра для каналов 2—4 рис. 4.19 составляют 64, 85 и 98% от истинного
максимума). Боковые гармоники утечки называются также боковыми лепестками,
поскольку в комплекснозначном представлении они чередуются в противофазе,
напоминая листья на ветке.
При очень мощных спектральных пиках их утечка
может простираться достаточно далеко, искажая близлежащие пики и затрагивая
даже соседние частотные диапазоны. Так в случае эпохи анализа 2 с для гармоники
с полуцелым числом периодов (канал 2 на рис. 4.19) утечка на расстоянии
5 Гц от основного пика 8,25 Гц (т. е. в соседнем бета-диапазоне) доходит
до 5% его истинного максимума. Поэтому при обработке результатов можно
вполне обнаружить ложный эффект синхронного изменения активности в двух
соседних, высоко- и низкоамплитудных частотных диапазонах.
Борьба с утечкой.
Обычно рассматриваются три основные способа борьбы с утечкой:
предварительная фильтрация сигнала;
увеличение разрешения по частоте;
использование корректирующих окон.
Фильтрация сигнала с оставлением полосы в интересующем
исследователя диапазоне частот позволяет исключить влияние утечки из соседних
диапазонов. Однако при необходимости совместного анализа всех диапазонов
и большом объеме обрабатываемых данных этот метод становится достаточно
трудоемким.
Увеличение разрешения по частоте позволяет уменьшить
вредное влияние утечки, поскольку спектральные линии становятся ближе,
уменьшая тем самым частотный интервал влияние утечки. Однако это требует
увеличения эпохи анализа, что неприемлемо в исследованиях кратковременных
отрезков ЭЭГ.
Корректирующие
окна представляют собой куполообразные
функции с максимумом в своей середине и амплитудой 1, с нулевым значением
на своих концах и шириной, равной длине реализации сигнала (рис. 4.20,
б).
На это окно умножается анализируемая реализация сигнала, после чего она
приобретает тоже куполообразный вид (рис. 4.20, в). Фактически эта
операция эквивалентна низкочастотной амплитудной модуляции (ср. рис. 4.18,
б).
Такое окно в спектральной области имеет свою собственную утечку с боковыми
лепестками, которые могут находиться в противофазе с лепестками утечки
сигнала (здесь имеется в виду противофаза спектра при его комплекснозначном
представлении, см. рис. 4.14, а), тем самым взаимно компенсируя
друг друга. В результате такой операции утечка из пика уменьшается, он
как бы стягивается, поджимается в более прямоугольную форму (ср. рис. 4.19,
б
и в, канал 2, при реализации корректирующих окон следует
также учитывать два важных момента: 1) при ненулевом среднем значении сигнала
применение окна вызывает ложные пики в нижних частотах, поэтому необходима
предвари-тельная коррекция нуля сигнала; 2) при умножении на куполообразное
окно уменьшается средняя амплитуда сигнала, что приводит к систематическому
занижению амплитуд спектра, поэтому необходима коррекция результирую-щего
спектра умножением его амплитуд на отношение площади прямоуголь-ного окна
к площади корректирующего окна) .
Рис. 4.20. Применение окон:
а —моногармонический сигнал; б — окно
Ханна;
в — результат умножения сигнала на окно
В области технических наук было предложено множество
окон, различающихся по степени уменьшения размытости спектральных пиков,
по крутизне их спада и по увеличению амплитуды: Бартлетта, Ханна, Хемминга,
Гауссово, Чебышева, Блекмана-Харриса, Кайзера-Бесселя и др. Наиболее известным
из них является окно фон Ханна, впервые использовавшем его при обработке
метеорологических данных. Оно имеет во временной области вид косинусной
функции (рис. 4.20, б):
xi' = 0,5*xi*(1+cos(t)),
(4.12)
где xi, xi' — амплитуды исходного
и взвешенного сигнала; t=2*3,14*(i-n/2)/n;
i=1,2,...,n
.
Дополнительные сведения о корректирующих окнах
и рекомендации по их выбору приведены в [29].
Однако в литературе не обращается внимание на
важный и принципиальный недостаток корректирующих окон: они совершенно
одинаково действует на любые пики. Поэтому уменьшение утечки наблюдается
только для тех истинных спектральных пиков процесса, которые при ДПФ попадают
в середину интервала между спектральными линиями (см. рис. 4.19, в,
канал 2). В случае же близости пиков к спектральной линии они вызывают
обратный негативный эффект уширения спектрального пика с понижением его
амплитуды (ср. рис. 4.19, б и в по каналам 1, 3, 4). Тем
самым окна в среднем в 50% дают позитивный эффект, а в 50% случаев — негативный
эффект (по крайней мере, в плане амплитудных искажений). Кроме того, максимальная
амплитуда после применения окон всегда уменьшается (от 50% до 35% для примеров
рис. 4.19). Для технических приложений подобные эффекты не критичны, поскольку
там окна преимущественно применяются в целях различения двух источников,
действующих на близких частотах, что для ЭЭГ совершенно неактуально.
Все вышесказанное не позволяет рекомендовать
использование окон при анализе ЭЭГ.
Амплитудная модуляция.
ЭЭГ сигналы являются нестационарными и в отличие от большинства
сигналов технического и физического происхождения характеризуются амплитудной
модуляцией, что приводит к дополнительным искажениям спектров. На рис.
4.18 приведены моногармонический и амплитудно модулированный сигналы и
их амплитудные спектры. При вычислении спектра модуляция проявляется появлением
боковых пиков половинной амплитуды (рис. 4.18г), при этом амплитуда основного
пика уменьшается (по сравнению с немодулированным сигналом) пропорционально
соотношению амплитуд в максимуме и минимуме модуляции. Тем самым при модуляции
в спектре появляются дополнительно еще два искажения: амплитудное и частотное
. Расстояние между основным и боковыми пиками (измеренное в числе спектральных
линий) определяется тем, сколько периодов модуляции помещается на эпохе
анализа. Тем самым боковые пики могут проникать далеко в соседние частотные
диапазоны, превнося в них дополнительные искажения (отметим, что в литературе
по анализу ЭЭГ этим искажениям не уделяется внимание, а в технических приложениях
этот эффект не трактуется как нежелательный).
Эффект частокола.
В технических приложениях в качестве недостатка БПФ упоминают так называемый
эффект частокола, возникающий вследствие дискретности спектральных линий
с шагом 1/T — мы как будто смотрим на действительный спектр процесса
сквозь щели забора. При этом «доски» этого забора могут нам заслонять узкие
высокоампитудные пики. Такой недостаток очень актуален, например, при поиске
узкополосных стационарных сигналов на фоне шума.
В области же исследований ЭЭГ мы имеем существенно
отличную ситуацию — там нет подобного типа сигналов, а сама ЭЭГ отличается
существенной нестационарностью. Поэтому на типичном поддиапазоне ЭЭГ шириной
4 Гц вполне достаточно иметь 4—8 спектральных линии (гармоник), т. е. вычислять
спектр на эпохах 1—2 с. При больших эпохах в спектре начинают проявляться
случайные амплитудные флюктуации и может оказаться полезным их сглаживание
методом скользящего среднего (ср. рис. 4.19, а и в).
Частотные характеристики
Частотные характеристики могут относиться к одному
сигналу (автоспектры) или же отражать взаимодействие двух сигналов (кросс-спектры).
Амплитудно-частотная характеристика
(АЧХ) или амплитудный спектр A(f) является наиболее информативной
и наиболее используемой в биологических и медицинских исследованиях частотной
характеристикой.
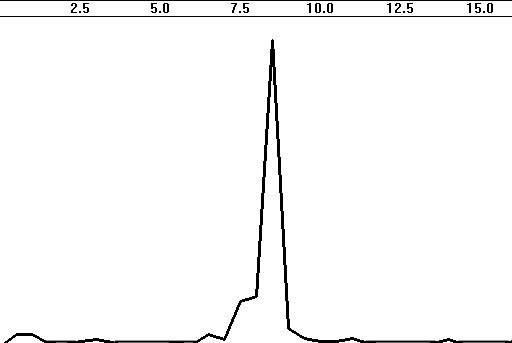
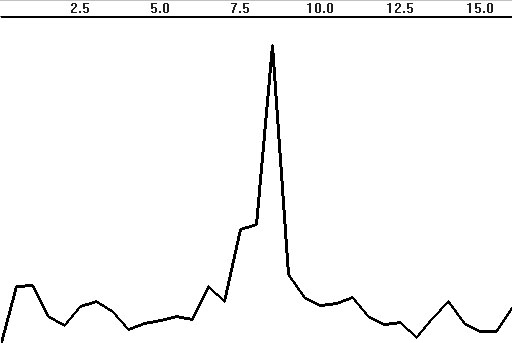
На рис. 4.21 приведены примеры спектров ЭЭГ. Как видно
из сравнения рис. 4.21а и б, уменьшение эпохи анализа ведет к значительному
снижению детализированности спектра (разрешения по частоте). С другой стороны,
большое разрешение ведет к появлению различных случайных флюктуаций (вследствие
влияния вытекания мощности, модуляции и др.), для нивелирования которых
может оказаться полезным сглаживание спектра (рис. 4.21в).
а)
б)
в)
г)
Рис. 4.21. Спектры ЭЭГ с доминированием альфа-ритма
на частоте 8 Гц:
а — АЧХ на эпохе 8 с; б — АЧХ на эпохе
2 с; в — АЧХ на эпохе 8 с с тремя сглаживаниями; г — спектр
мощности на эпохе 2 с
Фазо-частотная характеристика
(ФЧХ) или фазовый спектр ф(f) представляет зависимость
фаз спектральных гармоник (по оси Y) от частоты (по оси Х). Следует учитывать,
что график ФЧХ (см. рис. 4.16, б) строится в области значений Y
от 180° до -180°, поэтому при непрерывном изменении фазы с выходом за эти
границы он продолжается с другой стороны графика, что создает иллюзию появления
ложных пиков. В исследованиях ЭЭГ ФЧХ практически не используется, поскольку
ранние исследования не выявили ее значимых корреляций с физиологическими
процессами.
Спектр мощности представляет
собой амплитудный спектр, возведенный в квадрат Р(f)=A(f)2.
Однако у спектра мощности по сравнению с АЧХ
есть три принципиальных недостатка: 1) интуитивно понятно, что амплитуда
спектральных гармоник измеряется в милливольтах регистрируемого на скальпе
напряжения, но далеко не просто понять, что означают измерения, выполненные
в милливольтах в квадрате; 2) человеческий ум легко ориентируется в линейных
соотношениях между несколькими переменными или измерениями, однако ему
намного труднее воспринимать нелинейные соотношения (в данном случае квадратичные);
3) если сравнить графики АЧХ и спектра мощности (см. рис. 4.19, б
и
г), то на последнем будут доминировать лишь отдельные пики (чаще
всего — один главный пик), остальные же будут иметь пренебрежительно малую
величину, тем самым соотношения взаимной значимости различных спектральных
составляющих будут визуально и численно резко искажены.
Поэтому спектр мощности следует признать неадекватной
человеческому восприятию характеристикой.. Однако, как показывает несложное
статистическое моделирование методом Монте-Карло эти два показателя эквивалентны
в плане выявления достоверно значимых межгрупповых различий (Для
этого достаточно сгенерировать m выборок с n измерениями по любому закону
распределения. Затем выполнить все (m2-m)/2 попарных сравнений средних
выборочных значений по любому статистическому критерию с вычислением уровней
значимости нулевых гипотез. Далее следует возвести все выборочные значения
в квадрат, повторить эту процедуру и сопоставить полученные уровни значимости).
Малая чувствительность
к точности исходных данных. Результаты спектрального анализа
поразительно устойчивы к изменению точности представления исходных данных.
Дело в том, что при вычислении любой спектральной гармоники производится
n усреднений амплитуды сигнала, где n — число отсчетов на эпохе
анализа. А в ходе усреднения устойчивость результата к точности представления
исходных данных многократно возрастает (пропорционально корню из n,
где n — число усреднений).
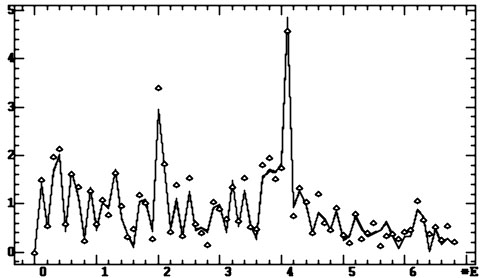
Рис. 4.22. Четыре спектра на эпохе 1024 при различной
точности исходных данных. Три спектра при динамическом диапазоне ЭЭГ в
12, 9, 5 и 2 двоичных разрядов (изображены линиями) зрительно неразличимы.
Спектр при динамическом диапазоне ЭЭГ в два двоичных разряда для визуального
отличия представлен ромбиками
В этом легко убедиться, выполнив простой эксперимент.
Возьмем типичную ЭЭГ-запись с несколькими выраженными пиками в низкочастотных
диапазонах, полностью использующую весь динамический диапазон 12-разрядного
АЦП (диапазон ±2048 в десятичном исчислении). Возьмем среднюю эпоху анализа
в 1024 отсчета (при частоте дискретизации 128 Гц это будет соответствовать
8 с). Далее выполним спектральный анализ для исходной записи (а)
и трех ее модификаций (b, c, d), в которых последовательно обнулим
три, семь и десять младших двоичных разрядов. Далее вычислим четыре спектра.
Уже простое визуальное сравнение этих спектров дает представление о малости
различий между ними (рис. 4.22).
Но пойдем далее и дадим количественную оценку
различиям. Для этого вычислим разности спектров b-а, c-а, d-а, нормируем
их на максимальную амплитуду спектра а, после чего выразим результат в
процентах и вычислим среднее значение, стандартное отклонение и максимальное
отклонение. Вот что мы получим: b) 0,035±0,026%, max=0,12%; c)
0,34±0,24%, max=1,4%; d) 3,5±2,4%, max=11%. Особенно поразителен
последний результат
d, поскольку в исходных данных мы оставили всего
лишь два значащих двоичных разряда. И, несмотря на это, мы получили в среднем
всего лишь 3,5% различия амплитуд этого спектра от точных значений. На
выделение доминирующих гармоник и сопоставление различных спектров такая
погрешность принципиально не скажется. Отсюда следует вывод: для задач
спектрального анализа в трех низкочастотных диапазонах вполне приемлемой
будет регистрации ЭЭГ с использованием 3—4-разрядного АЦП.
Кросс-спектральные характеристики
Кросс-спектральные характеристики предназначены для
оценки различных аспектов связи двух сигналов ЭЭГ, регистрируемых с двух
отведений.
Кросс-спектр.
двух процессов x(t) и y(t) вычисляется как произведение спектра
X(f)
на спектрY(f) в его комплексно сопряженной форме Y*(f):
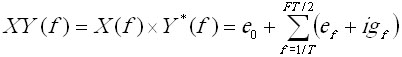 ,
(4.3)
Имея
,
(4.3)
Имея 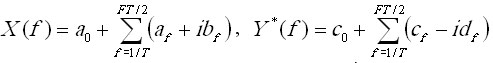 , и выполняя
почастотное умножение компонент X(f), Y*(f) с
выделением действительных и мнимых составляющих результата получаем выражения
для составляющих кросс-спектра:
ef = afcf+bfdf;
gf = afdf–bfcf.
(4.5)
Отсюда мощность кросс–спектра равна:
, и выполняя
почастотное умножение компонент X(f), Y*(f) с
выделением действительных и мнимых составляющих результата получаем выражения
для составляющих кросс-спектра:
ef = afcf+bfdf;
gf = afdf–bfcf.
(4.5)
Отсюда мощность кросс–спектра равна:
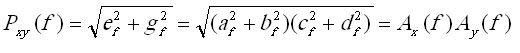 (4.4)
то есть равна произведению амплитуд спектров двух процессов, является
квадратичной оценкой, измеряемой в мкВ2. Линейная оценка амплитуды
кросс-спектра или кросс-АЧХ, соответственно, равна
(4.4)
то есть равна произведению амплитуд спектров двух процессов, является
квадратичной оценкой, измеряемой в мкВ2. Линейная оценка амплитуды
кросс-спектра или кросс-АЧХ, соответственно, равна 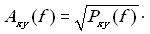 .
.
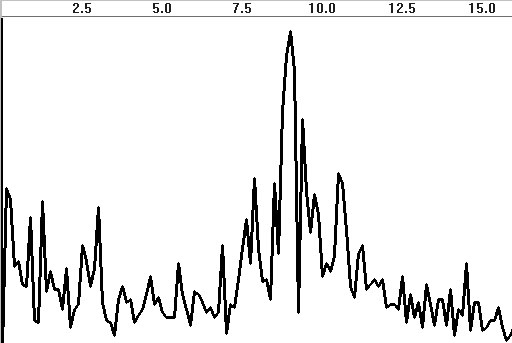
График кросс-АЧХ
(рис. 4.23а) наглядно показывает, на каких частотах в обоих процессах присутствуют
высокоамплитудные и сравнимые по величине гармоники. Как видно из рис.
4.23а, основные амплитуды кросс–спектра сосредоточены в районе 8 Гц альфа–диапазона,
что типично для затылочных отведений ЭЭГ в состоянии релаксации. Кроме
того, пики взаимной активности меньшей амплитуды наблюдаются в диапазонах
дельта и тета. Из–за высокого разрешения по частоте график содержит много
случайных флюктуаций, поэтому может оказаться полезным его сглаживание.
В исследованиях ЭЭГ кросс-АЧХ как оценочный показатель самостоятельного
применения не получил.
а)
б)
Рис. 4.23. Кросс-спектры ЭЭГ:
а — амплитудный; б — фазовый
Кросс-фазовый спектр фxy(f)=arctg(gf/ef)
после подстановки выражений (4.6) для gf и ef
и несложных тригонометрических преобразований представим в виде фxy(f)=фx(f)-фy(f),
то есть является разностью фаз двух спектров.
Как видно из рис. 4.23б, изменение кросс–фазы
носит достаточно случайный характер в связи с влиянием эффектов вытекания
мощности, амплитудной модуляции и переходов фазы через границы -180 +180о,
что затрудняет ее использование и интерпретацию.
На начальном этапе исследований кросс-фазу как
разность фаз двух процессов пытались интерпретировать как индикатор временной
задержки в передаче взаимодействия от одного процесса к другому. Однако
значимых результатов в этом направлении получено не было, и кросс-фаза
в современных исследованиях практически не используется.
Когерентность.
Еще одной кросс-спектральной характеристикой является функция когерентности,
и именно она практически используется для оценки степени взаимосвязи двух
процессов (подробнее см. ниже в разд. оценки синхронности ЭЭГ).
Неоднозначность интерпретации.
В отношении всех кросс–спектральных характеристик следует особо подчеркнуть,
что наличие связи двух процессов могут доказать не результаты проведенного
анализа, а только физиологические и анатомические основания. Результаты
же анализа могут лишь указать на целесообразность поиска таких оснований.
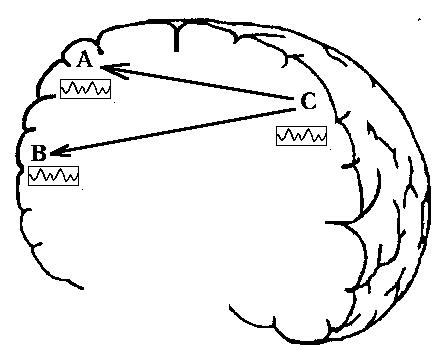
Рис. 4.24. К неоднозначности интерпретации кросс-спектральных
связей
Пусть мы регистрируем ЭЭГ в двух отведениях
А и В (рис. 4.24) и в результате кросс–спектрального анализа обнаруживаем
большую аутентичность этих процессов. Однако реально между этими отведениями
может не существовать никакой причинной связи, а аутентичность их определена
влиянием источника С в другой области головного мозга, анатомически связанного
с обоими отведениями А и В.
Обобщенные спектральные показатели
Как было отмечено выше, амплитудный спектр является
основной используемой в исследованиях ЭЭГ частотной характеристикой. Однако
вследствие погрешностей ДПФ амплитуды отдельных гармоник подвержены влиянию
случайных факторов как в отношении их последовательного распределения по
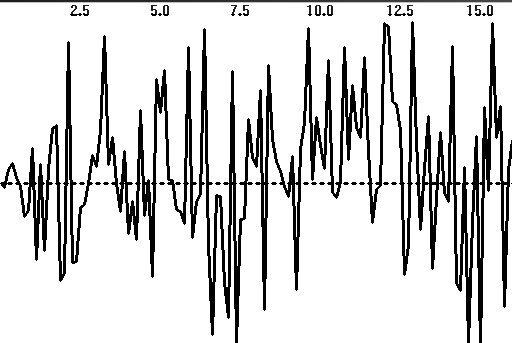
частотам, так и на последовательных эпохах анализа (рис. 4.25).
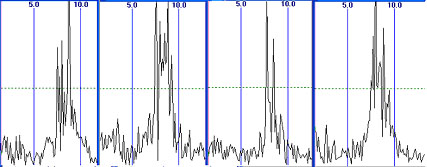
Рис. 4.25. Случайная вариабельность амплитуд спектральных
гармоник на четырех последовательных эпохах длительностью 8 с в затылочном
отведении О2
Тем самым эти амплитуды не могут использоваться
в качестве оценочных показателей. Более того, поскольку ЭЭГ не является
суммой гармонических колебаний, а нейронные структуры не являются гармоническими
осцилляторами, то амплитуды отдельных гармоник лишены физиологического
смысла. Поэтому, по крайней мере, в отношении статистической устойчивости
более предпочтительно использование усредненных амплитудных и частотных
оценок.
На основе любой спектральной характеристики могут
быть вычислены обобщенные спектральные показатели для всех интересующих
исследователя частотных диапазонов. В качестве таких показателей в ЭЭГ-анализаторах
обычно фигурируют следующие (рис. 4.26):
Аmax — максимальная амплитуда спектра в частотном диапазоне;
Fmax — частота максимальной по амплитуде гармоники;
Аср — средняя амплитуда спектра в частотном диапазоне;
Fcp — средневзвешенная частота, соответствует центру тяжести
фигуры, ограниченной кривой спектра в диапазоне, вычисляется по формуле:
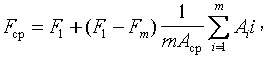 (4.13)
где m — число гармоник в частотном диапазоне; F1, Fm
— частотные границы диапазона; Аi — амплитуда i-й гармоники;
(4.13)
где m — число гармоник в частотном диапазоне; F1, Fm
— частотные границы диапазона; Аi — амплитуда i-й гармоники;
В исследовательской практике из этих показателей
наиболее употребительным является Аср.
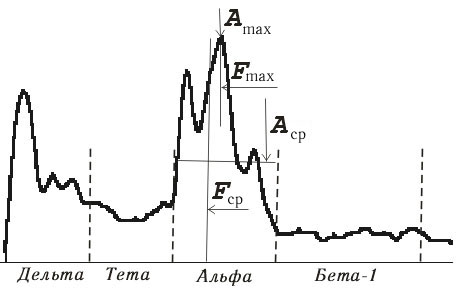
Рис. 4.26. Обобщенные спектральные показатели на примере
альфа-диапазона
Недостатки. Следует отметить, что рассмотренным
показателям, как и исходным ненвтуральным амплитудным и частотным оценкам
ЭЭГ, свойственен ряд погрешностей и случайных флюктуаций, присущих самим
частотным характеристикам (см. выше). Поэтому предпочтительнее использовать
натуральные оценки периодометрического анализа или огибающей ЭЭГ.
Анализ по эпохам и усреднение
спектров
Для исследования временной эволюции спектральных
показателей продолжительную ЭЭГ-запись разбивают на последовательные эпохи
более короткого размера, на каждой из которых выполняется частотный анализ.
Часто для получения более гладких зависимостей от времени эпохи выбирают
с определенным взаимным перекрытием (до 50%). Для наглядного визуального
представления эволюции избранного показателя обычно используют форму столбиковых
диаграмм по эпохам (горизонтальная ось времени) с построением серии диаграмм
в порядке отведений. Другим способом представления результатов является
серийное топографическое картирование по эпохам или в режиме динамической
мультипликации.
Для выявления наиболее стабильных спектральных
составляющих на длительных временных интервалах вычисляют усредненные по
эпохам частотные характеристики (усреднение производится для каждой спектральной
гармоники отдельно).
Оценки синхронности ЭЭГ
В предыдущх разделах было показано, что одной из
основных используемых в практике показателей является амплитуда изменения
ЭЭГ в отдельных отведениях, которая может быть оценена по амплитудному
спектру. Вторым практически важным показателем ЭЭГ является оценка взаимо-связи,
взаимовлияния, взаимодействия процессов в парах отведений. Для этого используются
различные показатели синхронности ЭЭГ, наиболее известным из которых является
функция когерентности.
Когерентность
Когерентность является ярким примером неадекватного
и некритического переноса кросс–частотной характеристики из технических
и физических приложений в исследования ЭЭГ, где она с 1950-х годов стала
постепенно широко и доминантно использоваться для оценки синхронности двух
процессов ЭЭГ (более детальные обоснования изложены в [47]). В своих же
базовых областях функция когерентности используется только для стационарных
процессов и как сугубо второстепенная характеристика — только для оценки
значимости других кросс–спектральных характеристик и для определения меры
влияния шума и/или нелинейности этих функций (цитируем
[20]: Малые значения когерентности могут указывать на незначимость на данной
частоте других кросс–спектральных характеристик или являться признаком
необходимости увеличения числа усреднений для ликвидации влияния шума)..
Более того, во времени в памяти затерялось, для чего и кем была введена
функция когерентности (развитие когерентного анализа преимущественно
было инициировано работа-ми Н. Винера в 1928-1930 гг. [Wiener N. Generalized
harmonic analysis. Acta Math. 1930, 55:182-195] применительно к задачам
оптики и квантовой механики, крайне далеких от исследований ЭЭГ).
Уже само определение когерентности во многих
фундаментальных источниках [13, 17, 19, 22] запутано и противоречиво,
включая и формулы, тождественно равные единице. Поэтому, развивая определение
из [20], дадим корректное математическое выражение для когерентности.
Будем использовать обозначение E[…] для
операции усреднения спектров на непересекающихся эпохах (метод Бартлетта
усреднения по ансамблю). Тогда выражение для квадрата когерентности будет
иметь вид:
 (4.7)
(4.7)
где 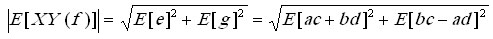 — геометрическое
усреднение векторов кросс-спектра по эпохам,
— геометрическое
усреднение векторов кросс-спектра по эпохам, 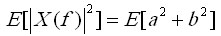 .—
арифметическое усреднение векторов авто-спектров.
.—
арифметическое усреднение векторов авто-спектров.
Наглядная интерпретация выражения (4.7) затруднительна, поэтому
рассмотрим модифицированное определение, которое назовем фазовой когерентностью.
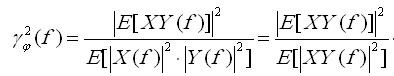 (4.8)
Его смысл поясним на фазовой плоскости (рис. 4.27), где имеются два
вектора кросс-спектра А и B с разными фазовыми углами для двух последовательных
эпох. При сложении в комплексной форме вектор В геометрически переносится
к концу вектора А, и результат сложения определяется длиной замыкающего
вектора А+В. При сложении по модулю |А|+|В| арифметически складываются
длины двух векторов. Понятно, что в общем случае результат комплексного
сложения будет меньше результата сложения по модулю, т. е. фазовая когерентность
будет меньше единицы. Увеличив в нашем рассуждении число векторов, мы поймем,
что такая когерентность характеризует степень синфазности двух процессов
или стабильности разности фаз векторов их индивидуальных спектров во времени.
При большой стабильности она близка к единице, а при произвольных вариациях
направленности она близка к нулю.
(4.8)
Его смысл поясним на фазовой плоскости (рис. 4.27), где имеются два
вектора кросс-спектра А и B с разными фазовыми углами для двух последовательных
эпох. При сложении в комплексной форме вектор В геометрически переносится
к концу вектора А, и результат сложения определяется длиной замыкающего
вектора А+В. При сложении по модулю |А|+|В| арифметически складываются
длины двух векторов. Понятно, что в общем случае результат комплексного
сложения будет меньше результата сложения по модулю, т. е. фазовая когерентность
будет меньше единицы. Увеличив в нашем рассуждении число векторов, мы поймем,
что такая когерентность характеризует степень синфазности двух процессов
или стабильности разности фаз векторов их индивидуальных спектров во времени.
При большой стабильности она близка к единице, а при произвольных вариациях
направленности она близка к нулю.
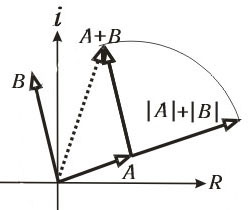
Рис. 4.27. Сложение векторов в комплексной форме
и по модулю
Отсюда предполагается, что при наличии физиологической
связи между двумя отведениями сигнал от одного отведения к другому будет
переда-ваться с достаточно стабильной задержкой во времени (или стабильным
фазовым сдвигом), что будет приводить к большому значению когерентности.
Однако ЭЭГ не является суммой гармонических колебаний, а нейронные структуры
не являются гармоническими осцилляторами, поэтому когерентная оценка конкретных
гармоник в двух отведениях не имеет физиологического смысла.
Сложнее обстоит дело с классической когерентностью
(4.7), поскольку она достаточно адекватно оценивает степень фазовой стабильности
только при близких по величине амплитудах кросс-спектра на соседних эпохах.
При сильном различии амплитуд она дает завышенные значения (в 1.5 и более
раз). Такой показатель, непонятно что и в каком соотношении оце-нивающий,
метрологически не может быть квалифицирован как измери-тельный инструмент.
Итак, для вычисления когерентности необходимо
усреднение нескольких векторов кросс-спектра, иначе результат будет тождественно
равен еди-нице. Для этого всю запись ЭЭГ предварительно разбивают на несколько
последовательных эпох меньшего размера, на каждой из которых вычисляют
кросс-спектр. Для статистической устойчивости оценок надо использовать
не менее 8-10 таких эпох, что делает когерентность неприем-лемой для анализа
ЭЭГ на коротких временных отрезках.
При этом значения когерентности будут меняться
в зависимости от нескольких от нескольких изначально выбранных условий
или установочных параметров: 1) число эпох в анализируемом участке ЭЭГ;
2) величина перекрытия или временного сдвига эпох; 3) использование корректирующих
окон при вычислении спектров; 4) использование сглаживания исходных спектров;
5) использование квадратичной ?2 или неквадратичной g
формы когерентности. Такой показатель, значения которого зависят от нескольких
установочных параметров (или «регулировочных ручек»), метрологически не
может быть квалифицирован как измерительный инструмент.
В фундаментальных трудах часто утверждается,
что когерентность отражает линейную связь двух процессов в частотной области
аналогично тому, как обычный коэффициент корреляции rxy
отражает степень линейной взаимосвязи двух процессов во временной области.
Это также не вполне корректно: 1) rxy, в частности, достаточно
линейно зависит от присутствия в сигналах шума, а зависимость g2
от уровня шума выраженно нелинейная; 2) значения rxy, в отличие от g2,
не зависят от амплитудных соотношений сигналов; 3) квадратичная форма rxy
практически не используется; 4) диапазон значений rxy
составляет +-1, а g2 — 0-1.
а)
б)
Рис. 4.28. Когерентность ЭЭГ, вычисленная с усреднением
на 8 эпохах длиной 8 с:
а — исходная; б — сглаженная 3 раза
Как видно из рис. 4.28а, когерентность, как и
фаза, подвержена частым и высоким случайным колебаниям. Здесь сказывается
влияние эффектов модуляции и вытекания мощности, в результате чего векторы
спектральных гармоник на соседних эпохах заметно «гуляют» по фазе.
Для нивелирования стохастичности применяют сглаживание
когерентности скользящим средним (рис. 4.28б). В данном случае на низких
частотах когерентность равна единице, и наблюдаются достаточно высокие
ее пиковые значения на отдельных частотах в диапазонах тета, альфа и бета-1.
Следует также обратить внимание на то, что в
некоторых ЭЭГ-анализаторах когерентность вычисляется по одной эпохе с усреднением
соседних гармоник кросс-спектра скользящим окном заданной ши-рины (метод
Даньелла). Это идет со времен некомпетентного внедрения математических
методов в электрофизиологию техническими энтузиастами. Отметим, что статистические
свойства такой «псевдокогерентности» совершенно не определены, а ее использование
нисколько не лучше измерения длины удава в попугаях.
Кроме того, когерентность предъявляет повышенные
требования к точности вычислений. В этом плане малые значения амплитуд
спектров вычисляются недостаточно точно, поскольку исходные данные представляются
только самыми младшими разрядами результата АЦП. Отсюда возникают дополнительные
случайные флюктуации когерентности во всем диапазоне ее значений. В случае
же нулевых значений спектра когерентность вообще не определена.
Многочисленные недостатки и погрешности когерентного
анализа приводят к тому, что результаты, получаемые в различных направлениях
иссле-дований ЭЭГ, являются несопоставимыми и прямо противоречащими друг
другу (см. во вводных обзорах [49, 50, 52-54]). Однако, сила традиции,
в том числе и в плане научных заблуждений, очень велика и переломить ее
далеко не просто и быстро.
Когерентная мощность.H1(f)
(передаточная функция или частотная характеристика) является еще одним
показателем, оценивающим связь двух процессов и используемым в отдельных
исследованиях ЭЭГ. Она определяет часть спектральной мощности, которая
когерентно (синфазно) передается от одного процесса x(t) к другому
y(t):
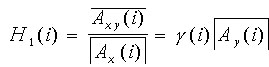 .
(4.11)
.
(4.11)
Тем самым H1(f) по сравнению с когерентностью учитывает
еще и амплитудное соотношение гармоник (в мкВ2), в чем состоит
ее определенное преимущество. По вышеприведенным соображениям предпочтительнее
использовать оценку в мкВ когерентной амплитуды Ax->y(f)
или корень квадратный из H1(f). Как видно из рис. 4.29,
пиковое значение Ax->y(f) наблюдается не только на доминирующей
частоте альфа-диапазона, но и в дельта-диапазоне, повышенная взаимная активность
в котором наблюдалась и в амплитуде кросс-спектра (см. рис. 4.23а). На
спектре Ax->y(f) менее проявлены случайные флюктуации,
свойственные когерентности (рис. 4.28а), но присущи и аналогичные
недостатки.
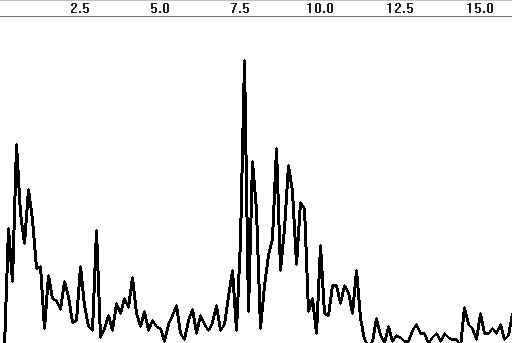
Рис. 4.29. Когерентная мощность ЭЭГ
Корреляционная синхронность
В качестве альтернативы когерентности были предложены
показатели [49], оценивающие синхронность ЭЭГ процессов по величине корреляций
между: нативными ЭЭГ, амплитудными и фазовыми спектрами и огибающими ЭЭГ.
Как свидетельствуют сравнения этих показателей [49], наиболее эффективным
в плане чувствительности к межгрупповым различиям является использование
огибающей ЭЭГ (см. также в разд. 4.4.7).
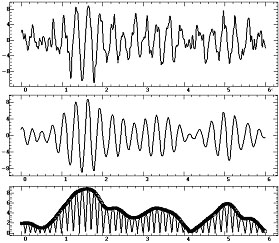
Рис. 4.30. Сверху вниз: фрагмент ЭЭГ, фильтрация альфа-ритма,
огибающая альфа-ритма на фоне абсолютных значений ЭЭГ
Огибающая ЭЭГ непосредственно представляет динамику
амплитудной модуляции ЭЭГ (рис.4.30), поэтому в качестве оценки синхронности,
в отличие от спектральных оценок, включая когерентность, она имеет прямой
и четкий физиологический смысл. Поскольку ЭЭГ суммарно отражает изменение
постсинаптических потенциалов, то амплитуда ЭЭГ повышается, когда эти потенциалы
начинают изменяться с большей синхронностью. Таким образом, корреляция
огибающих оценивает степень синхронности в синхронности/асинхронности изменении
постсинаптических потенциалов в сравниваемых парах отведений.
Как показали результаты ряда специальных исследований
[49, 50, 52-54] использование оценок корреляционной синхронности огибающих
ЭЭГ позволяло выявлять межгрупповые различия со значительно большей эффективностью,
чем в случае использования других показателей. При этом в большинстве случаев
надежность межгрупповой классификации приближается к 100%.
Топографическое картирование
Методы топографического представления распределения
потенциалов на поверхности головного мозга в западном мире начали развиваться
и внедряться в физиологию в середине 50-х годов. Вскоре, благодаря пионерским
работам М.Н. Ливанова по энцефалоскопии, это методы начали развиваться
и в СССР. Однако в начале 90-х после перевода довоенных японских научных
журналов выяснилось, что японские ученые значительно опередили своих западных
коллег, приступив к созданию ЭЭГ-топографии еще в начале 40-х годов. После
появления растровых дисплеев для ПЭВМ данный метод постепенно приобрел
(с 1979 г.) современную форму цветного топографического картирования.
Постановка задачи.
Основной задачей картирования является предоставление электрофизиологу
адекватной и быстро зрительно воспринимаемой картины распределения значений
заданного ЭЭГ-показателя на скальпе. Точные значения ЭЭГ-показателя известны
только в местах наложения электродов, межэлектродное же пространство представляет
собой область неизвестного, своеобразное «белое пятно». С другой стороны,
специальные физиологические исследования показывают, что при расстоянии
между электродами 2—4 см получаемая картина распределения является достаточно
адекватной и гладкой, поскольку области пиковых значений ЭЭГ-показателя
охватывают значительно большее пространство. Таким условиям отвечает стандартная
схема наложения электродов «10-20%». Таким образом, математическая задача
картирования состоит в адекватной интерполяции измеренных значений ЭЭГ-показателя
на окружающее межэлектродное пространство.
Подходы.
К решению этой задачи может быть много подходов. Так, в первых мощных математических
пакетах Sirfer (научная графика) и IMSL (статистика) для DOS использовались
достаточно сложные и многоступенчатые алгоритмы: сначала на точках измерения
строился минимальный граф (без пересекающихся ребер), после чего интерполяция
производилась по ребрам этого графа, а затем она пошагово распространялась
на внутриграфовые области с последующим сглаживанием. В зависимости от
сложности вычислений могла использоваться линейная, параболическая или
сплайновая интерполяция. С другой стороны, при создании некоторых ЭЭГ-анализаторов
(в том числе и современных) привлекаемые технические энтузиасты применяли
собственные оригинальные творческие решения, поэтому выдаваемые там карты
подчас имеют довольно экзотический вид, своеобразно «улучшающий» реальное
распределение потенциалов.
Полевой метод.
В противовес этому и в целях упрощения и унификации еще в первой версии
CONAN-1.5 (1993 г.) был реализован полевой метод картирования, который
представляется естественным, простым, понятным и универсальным.
Он следует из фундаментальных физических законов
обратных квадратов для распределения потенциалов гравитационного (Ньютон),
электрического (Кулон) и ряда других полей. Согласно этому методу измеренные
значения ЭЭГ-показателя под электродами ei, i=1-n
рассматриваются как источники поля (заряды), тогда напряженность поля ek
в любой k-й точке скальпа (рис. 4.31, а) вычисляется по формуле:
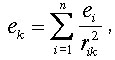 ,
(4.14)
где rik — расстояния от «зарядов» до промежуточных
точек.
,
(4.14)
где rik — расстояния от «зарядов» до промежуточных
точек.
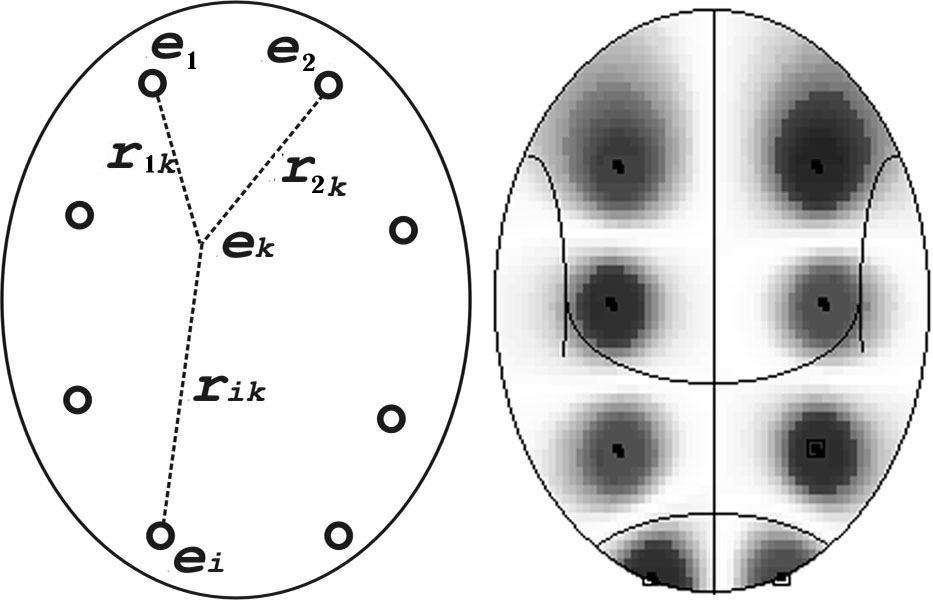
а)
б)
Рис. 4.31. Полевой метод картирования:
а — принципиальная схема; б —пример
условной карты с шахматным чередованием минимумов и максимумов (в черно-белом
изображении они выглядят одинаково темно)
В одномерном приближении этот метод дает результат,
близкий к интерполяции кубическими сплайнами при значительно меньшем объеме
вычислений. Тем самым он не привносит ничего лишнего и постороннего в топографическую
картину, лишь сглаженно распространяя измеренные значения ЭЭГ-показателя
и тем самым делая их доступными для целостного и моментального зрительного
восприятия исследователем, в чем собственно и состоит главная цель картирования.
Обычно для визуализации карт используется полицветная
шкала от синего к красному (радужная шкала), которая масштабируется по
наблюдаемому диапазону значений картируемого показателя.
Картирование может производиться по каждому из
вышерассмотренных ЭЭГ-показателей или любому другому с использованием нескольких
форм визуального представления. Их перечень приведен в начале раздела.
Картотека
Общее назначение картотеки охарактеризовано в начале
раздела. Основными ее функциями является усреднение и сравнение карт.
Усреднение значений картируемого показателя производится
по каждому отведению для однородных карт (у которых одинаковы система отведений,
ЭЭГ-показатель, частотные диапазоны, а также другие показатели по выбору
исследователя). Для усредненной карты запоминается число усреднений, средние
значения показателей и их дисперсии.
Последовательности значений ЭЭГ-показателя двух
карт по отведениям в определенном приближении можно рассматривать как парные,
не нормально распределенные выборки. Поэтому для оценки статистических
различий двух карт (нативных, усредненных) целесообразно использовать непараметрические
статистические критерии: а) парных различий в средних выборочных значениях
(Вилкоксона); б) интегральных различий в форме распределения (Колмогорова-Смирнова);
в) непараметрическая корреляция (Спирмана). В зависимости от того, какие
различия исследователю представляются более важными, он преимущественно
ориентируется на тот или иной критерий.
При сравнении нативной и усредненной карт имеется
также возможность оценки различий дифференцированно по парам отведений
с использованием Z-значений — разность двух значений показателя, деленная
на стандартное отклонение. В качестве делителя можно с определенным приближением
использовать среднее из двух стандартных отклонений. При интерпретации
результатов в первом приближении можно ориентироваться на свойства нормального
распределения, где вероятности Z-различий составляют: Z>1 — 0,16;
Z>2 — 0,026; Z>3 — 0,0028. Критическое Z-значение для уровня значимости
различий 0,05 составляет Zкр=1,65. Для наглядного визуального представления
результатов сравнения обычно строят карту различий в Z-значениях.
Корреляционный анализ
Корреляционный анализ включает вычисления коэффициентов
корреляции, а также авто- и кросскорреляционных функций. В докомпьютерном
прошлом корреляционный анализ был широко распространен как заместитель
спектрального анализа в связи с доступностью аналоговых вычислителей. В
современности модификация метода находит применение в качестве коррелятора
для поиска образцов.
Коэффициент корреляции
(КК) Пирсона (параметрический) является индикатором линейной
связи между парными переменными или парными выборками X и Y и применяется
в случае нормально распределенных исходных данных. Он вычисляется как отношение
ковариации двух переменных к их стандартным отклонениям:
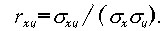 (4.15)
Значение, близкое к +1 или –1, говорит о сильной
прямой или обратной корреляции. Значение, близкое к 0, указывает на отсутствие
линейной связи, но не исключает возможности нелинейной связи между переменными.
Высокая корреляция не обязательно означает наличие причинной связи между
переменными, поскольку обе они могут зависеть от третьей переменной (аналогично
вышерассмотренным кросс-спектральным характеристикам, см. рис. 4.21).
(4.15)
Значение, близкое к +1 или –1, говорит о сильной
прямой или обратной корреляции. Значение, близкое к 0, указывает на отсутствие
линейной связи, но не исключает возможности нелинейной связи между переменными.
Высокая корреляция не обязательно означает наличие причинной связи между
переменными, поскольку обе они могут зависеть от третьей переменной (аналогично
вышерассмотренным кросс-спектральным характеристикам, см. рис. 4.21).
В данном случае в качестве парных выборок выступают
два участка равной длительности, относящиеся к одному ЭЭГ-отведению (автокорреляция)
или к двум отведениям (кросскорреляция). Высокая положительная корреляция
означает синфазность или синхронность изменения двух сигналов, когда увеличению
одного сигнала соответствует увеличение другого сигнала, и так же в отношении
уменьшения сигналов. Высокая отрицательная корреляция означает синхронную
противофазность сигналов, когда увеличению одного сигнала соответствует
уменьшение другого. При асинхронном изменении сигналов корреляция будет
близка к нулю.
Значимость КК оценивается по критерию Стьюдента
с вычислением критического значения:
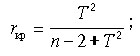 (4.16)
где
(4.16)
где 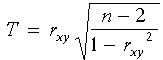 — статистика Стьюдента
с n–2 степенями свободы.
— статистика Стьюдента
с n–2 степенями свободы.
Если rxy<rкр,
коэффициент корреляции считается незначимым (не отличным от нуля).
Корреляционная функция
(КФ) представляет собой зависимость коэффициента корреляции
rxy(t)
между двумя участками сигнала x, y в зависимости от временного сдвига
t
между ними. Если участки относятся к одному сигналу, то функция называется
автокорреляционной, если же участки относятся к разным сигналам, то — кросскорреляционной.
Определение.
В математической теории КФ определяется через интегралы применительно к
непрерывным и стационарным сигналам бесконечной протяженности.
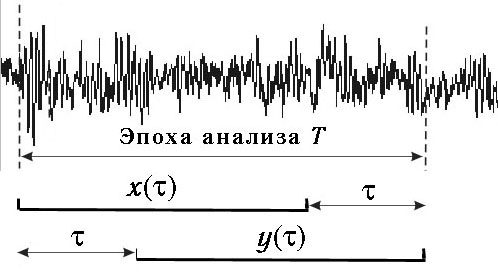
Рис. 4.30. Вычисление «классической» корреляционной
функции
|
Рис. 4.31. Вычисление интервальной корреляционной
функции
|
В технических приложениях это определение было модифицировано
применительно к сигналам дискретизованным и ограниченной протяженности
следующим образом (рис. 4.30). Выбирается эпоха анализа Т из имеющейся
реализации сигнала. На этой эпохе в зависимости от временного сдвига t
для вычисления коэффициента корреляции rxy(t)
выбираются два участка: а)
x(t) на начальном участке эпохи анализа
0 — Т-t ; б) y(t) на конечном
участке эпохи анализа t — Т. Для определенности
далее будем называть такой способ вычисления КФ техническим.
В докомпьютерную эпоху этот метод был перенесен
в электрофизиологию техническими энтузиастами без критического осмысления.
В свое время это вызвало много обсуждений и вопросов, например: с какого
Т
начинать и при каком t заканчивать вычисления?
Недостатки.
Однако при таком переносе метода было упущено из внимания главное: при
разных t мы имеем дело с участками разной протяженности!
А для сопоставимости коэффициентов корреляции это допустимо только в случае
стационарности процессов, которые сохраняют свои статистическое свойства
(в частности, среднее значение и дисперсию) на всей своей протяженности.
В случае же ЭЭГ мы имеем субстанциально нестационарный процесс, и его участки
разной длительности имеют разные статистические свойства. Важным также
является зависимость критического значения коэффициента корреляции от размера
выборки. Поэтому равные величины на одном краю КФ могут быть значимы, а
на другом — нет. Еще одной неадекватностью технического определения КФ
является то, что при вычислении rxy=sxy/(sxsy)
ковариация sxy вычисляется на каждом
шаге для отрезков длиной Т-t, а вариации
sx, sy
— однократно для всей эпохи Т.
Интервальная КФ.
Исходя из этого, еще в первой версии CONAN-1.5 (1993 г.) была предложена
модификация вычислений, названная интервальной КФ (рис. 4.31).
На реализации сигнала выбирается фиксированный
корреляционный образец x длиной Dt,
от которого позиционируется эпоха анализа
Т. Для вычисления корреляций
с образцом x при каждом
t берутся равноразмерные
участки y, сдвинутые относительно x на величину
t.
а)
б)
Рис. 4.32. Корреляционные функции ЭЭГ-сигнала рис.
4.30:
а — классическая; б — интервальная
Сравнение. Различие
двух методов вычисления КФ иллюстрирует рис. 4.31. Для технической КФ (рис.
4.31, а) при небольших сдвигах могут наблюдаться высокие значения
вследствие большой длительности отрезков и незначительности их интегральных
различий. С увеличением сдвига характерно систематическое уменьшение значений
КФ в связи с уменьшением длины отрезков и возрастанием их интегральных
различий. Интервальная же КФ периодически повторяет высокие значения при
сдвиговых воспроизведениях образца (рис. 4.32, б). В отличие от
технической КФ для интерпретации динамики интервальной КФ легко найти визуальные
основания. Так, например, начальные малые значения КФ на рис. 4.32, б
определены резким изменением ритмики сигнала на начальном временном участке
рис. 4.31.
Тем самым интервальная КФ является удобным средством
выявления доминирующих корреляций и их лагов (задержек). Высокие корреляции
будут наблюдаться тогда, когда при некотором временном сдвиге ритмика участка
ЭЭГ будет хорошо повторять ритмику образца. В случае кросскорреляции это
может интерпретироваться как задержки в передаче взаимодействия от одного
процесса к другому. В случае автокорреляции высокие значения КФ могут интерпретироваться
как повторения заданного функционального состояния. В частном же случае
корреляционная функция может использоваться для поиска в сигналах заданных
характерных образцов.
Следует подчеркнуть, что коэффициент корреляции
и корреляционная функция позволяют отчетливо выявлять степень аутеничности
лишь доминирующих (обычно низкочастотных) ритмов, однако это ограничение
может быть в значительной степени снято посредством предварительной низкочастотной
режекции. Кроме того, этот метод позволяет уловить более быстротечные изменения
синхронности двух процессов, чем кросс-спектральные характеристики, поскольку
для своего вычисления он допускает значительно более короткие временные
отрезки.
Периодометрический анализ
Периодометрический анализ возник и получил широкое
распространение в докомьютерную эпоху, когда доминировали ручные измерения
на бумажных записях ЭЭГ. Однако он не потерял своей значимости и в настоящем,
позволяя во многом дополнять результаты спектрального анализа.
Периодометрический анализ ставит своей целью
исследование распределения амплитуд и частот заданного ритма. Под ритмом
понимаются гармонические колебания в любом заданном частотном диапазоне,
в частности — в стандартных частотных диапазонах. Собственно анализ предваряет
фильтрация с выделением из сигнала гармонических составляющих в заданном
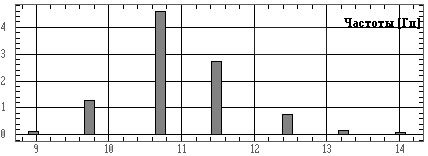
частотном диапазоне (рис. 4.33).
По отфильтрованному сигналу вычисляются амплитуды
Ai
и периоды Ti (i=1-n) волновых колебаний. Для статистической
значимости последующих оценок необходимо, чтобы n>20-30, что определяет
минимальный временной интервал наблюдения. Так, в случае альфа-ритма длина
эпохи анализа должна быть не менее 2-3 с.
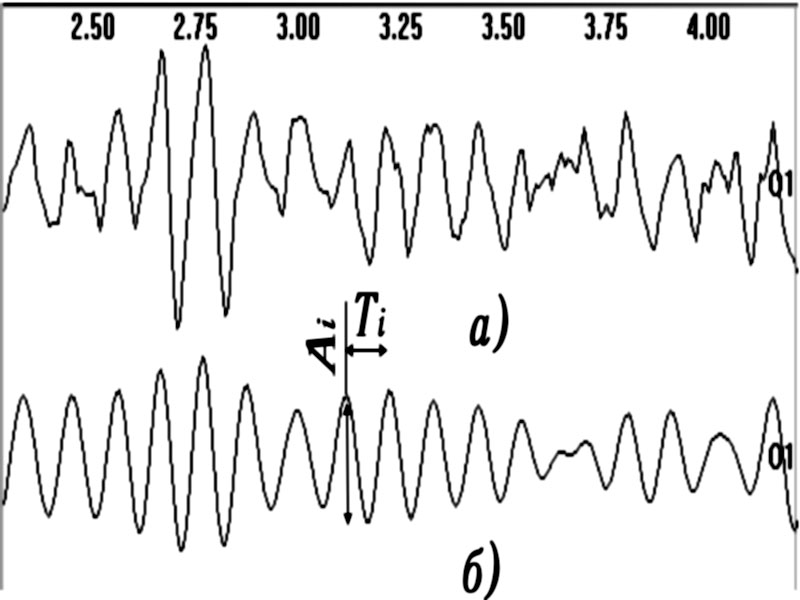
Рис. 4.33. Периодометрический анализ:
а — исходный ЭЭГ-сигнал; б — результат
фильтрации с полосой пропускания в альфа-диапазоне
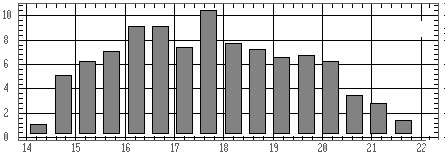
По вычисленным значениям строятся гистограммы распределения
амплитуд и периодов (или частот fi=1/Ti) ритма (рис. 4.34)
с вычислением средних значений и стандартных отклонений.
а)
б)
Рис. 4.34. Гистограммы распределения:
а — амплитуд ритма; б — частот ритма
Далее вычисляются следующие показатели:
процент содержания ритма в записи на основе общей
длительности ST периодов колебаний, соответствующих
данному ритму;
процент модулированного ритма, т. е. относительное
содержание в ST длительности участков
ритма, включающих не менее трех периодов с последовательно возрастающими
или последовательно убывающими амплитудами;
средняя нестабильность частоты ритма, вычисляется по средней
абсолютной разности между длительностью соседних периодов df=1/(S|Ti-1-Ti|/n).
Фильтрация, огибающая, сглаживание
Фильтрация предназначена для выделения из сигнала
интересующего исследователя диапазона частот и удаления шумовых или не
представляющих интерес составляющих. При анализе экспериментальных данных
используются цифровые фильтры, реализованные вычислительными средствами.
Наиболее употребительны фильтры Баттерворда и Чебышева-1,2, которые являются
эквивалентами одноименных и популярных аналоговых фильтров.
Эти фильтры пропускают гармонические колебания
без искажения их формы. Однако в результате фильтрации возникают амплитудные
и фазовые искажения.
Амплитудные искажения.
Амплитудно-частотная характеристика (АЧХ) фильтра зависит от его типа и
порядка. АЧХ представляет отношение амплитуд гармоник на выходе к амплитудам
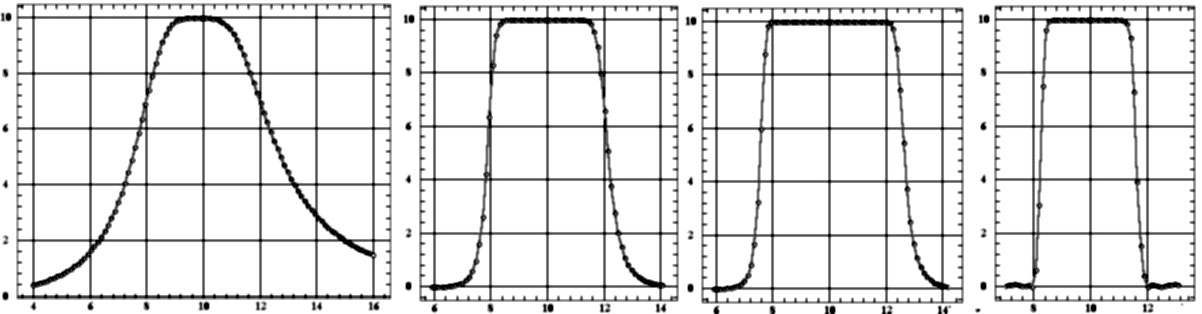
на входе фильтра в зависимости от частоты. На рис. 4.35 приведены АЧХ четырех
фильтров с полосой пропускания 8—12 Гц (альфа-диапазон). В полосе пропускания
АЧХ близка к 1 (гармоники пропускаются фильтром), а в полосе задержания
— близка к 0 (гармоники подавляются по амплитуде).
а)
б)
в)
г)
Рис. 4.35. Амплитудно-частотные характеристики фильтров
с полосой пропускания 8-12 Гц:
а — Баттерворда 2-го порядка; б — Баттерворда
8-го порядка; в — Чебышева-1 8-го порядка; г — Чебышева-2
8-го порядка
На границах полосы пропускания (частоты среза) наблюдается
спад АЧХ, крутизна которого (крутизна среза) увеличивается с повышением
порядка фильтра. Как видно из сравнения рис. 4.35, а и б,
фильтр Баттерворда 2-го порядка по сравнению с фильтром 8-го порядка имеет
заметно более пологие срезы АЧХ.
В связи с конечной крутизной срезов (неотвесными
срезами) имеют место два искажения: 1) в сигнале частично подавляются гармоники
(уменьшается их амплитуда), близлежащие к частоте среза со стороны полосы
пропускания; 2) частично пропускаются гармоники (с уменьшением их амплитуды),
близлежащие к частоте среза в полосе задержания.
Фильтры Баттерворда сохраняют определенный баланс
между этими двумя искажениями. Фильтр Чебышева-1 минимизирует первую погрешность,
его АЧХ во всей полосе пропускания близка к 1 (рис. 4.35, в). Фильтр
Чебышева-2 минимизирует вторую погрешность, его АЧХ во всей полосе задержания
близка к 0 (рис. 4.35, г). В целом фильтры Чебышева при том же порядке
имеют большую крутизну среза, чем фильтры Баттерворда.
Отметим также, что при увеличении порядка фильтра
увеличивается объем и время вычислений (снижается быстродействие фильтра),
но это является критичным только при использовании фильтрации в режиме
реального времени, когда процесс фильтрации может не успевать за реальным
сигналом, превышая длительность одного интервала дискретизации АЦП.
Присутствие нелинейностей.Этот
недостаток относится к фильтрам Чебышева. Фильтры Чебышева-1 имеют нелинейности
в виде колебаний АЧХ в полосе пропускания, а фильтры Чебышева-2 — в полосе
задержания. Однако эти нелинейности невелики по амплитуде (на рис. 4.35
в,
г
они практически незаметны из-за высокого порядка фильтров) и не столь актуальны
для области физиологии по сравнению с техническими приложениями, где они
могут затруднить разделение узких близлежащих спектральных пиков. Кроме
того, уровень нелинейности АЧХ регулируется специальным параметром e фильтра
Чебышева. Уменьшение e вызывает соответствующее снижение быстродействия,
но это может быть критично лишь при фильтрации в режиме реального времени.
Фазовые искажения
являются одним из основных погрешностей, присущих классической фильтрации.
Они являются следствием метода последовательного приближения, на котором
базируется фильтрация, а именно: чтобы в любой момент времени t
оценить амплитуду i-й гармонической составляющей сигнала с периодом
Тi
необходимо ее наблюдать в течение Тi с момента t. Тем самым
каждая гармоника в результате фильтрации приобретает задержку во времени
или фазовый сдвиг, пропорциональный Тi или 1/fi, т. е. обратно
пропорциональный частоте гармоники fi. На фазовые искажения также
влияет порядок фильтра и полоса частот.
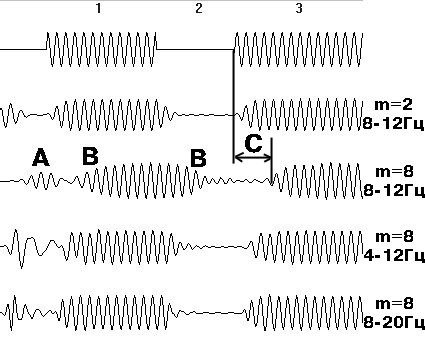
Рис. 4.36. Фазовые искажения при фильтрации:
канал 1 — исходный сигнал частотой 11 Гц; каналы 2-5
— результаты фильтрации в разных частотных диапазонах фильтрами Баттерворда
m-го порядка; обозначения искажений: А — начального приближения; В — переходные
при смене характера сигнала; С — временной сдвиг
Сложный характер фазовых искажений удобно продемонстрировать
на упрощенном модельном примере рис. 4.36. На канале 1 приведен полигармонический
сигнал с двумя участками нулевой амплитуды, а на каналах 2—5 показаны результаты
фильтрации различными фильтрами. Здесь присутствуют искажения начального
приближения (А), переходные амплитудные искажения при резкой смене характера
сигнала (В) и постоянный временной фазовый сдвиг (С). Фазовые и переходные
искажения увеличиваются с повышением порядка фильтра (ср. каналы 2 и 3).
Для гармоник, лежащих в середине полосы пропускания, эти искажения уменьшаются
при расширении полосы как в сторону низких, так и в сторону высоких частот
(каналы 4, 5).
Поскольку фазовый сдвиг обратно пропорционален
частоте гармоники, то для широкополосных сигналов (с многими гармониками
высокой амплитуды) сложение их фазовых сдвигов может приводить к дополнительному
искажению формы сигналов. Однако для области физиологии такой характер
сигналов нетипичен.
Фурье-фильтрация.
Указанные погрешности классической фильтрации побудили уже в первой версии
CONAN-1.5 (1993 г.) предложить новый для электрофизиологии метод Фурье-фильтрации,
основанный на использовании двукратного Фурье-преобразования. После первого
преобразования сигнала в частотную область из комплекснозначного спектра
удаляются гармоники в заданном диапазоне частот, после чего обратным Фурье-преобразованием
по усеченному спектру восстанавливается отфильтрованный сигнал во временной
области.
Принципиальными достоинствами такого метода по
сравнению с классическими фильтрами являются:
практически полное отсутствие фазовых искажений;
практически бесконечная крутизна среза, вследствие
чего частотная характеристика фильтра близка к прямоугольной — полное подавление
гармоник в полосе задержания и отсутствие искажений в полосе пропускания;
минимальные амплитудные искажения, имеющие место
только на границах полосы задержания за счет незначительного влияния эффектов
утечки и амплитудной модуляции, уменьшающегося с увеличением разрешения
по частоте.
При реализации Фурье-фильтрации нужно учитывать
ограничение на длину обрабатываемой реализации сигнала. Поэтому фильтрацию
длительных записей приходится производить поинтервально. Поскольку фазы
гармоник на соседних интервалах в общем случае не совпадают, на стыках
интервалов могут возникать небольшие амплитудные скачки, визуально более
заметные при полосовой фильтрации в низкочастотном диапазоне. Для нивелирования
этих скачков интервалы фильтрации следует выбирать с небольшим перекрытиям
и усреднением результатов (Отметим, что этот эффект сказывается
только при фильтрации сигналов большой протяженности. Так, при работе ДПФ
на интервалах до 8192 отсчета для сигнала с частотой дискретизации 128
Гц во временном выражении это будет соответствовать 64 с. Поскольку большинство
ЭЭГ-записей выпол-няются и анализируются на значительно меньших интервалах
наблюдения, проблема стыковочных концов для них не актуальна. Кроме того,
сглаживание стыков имеет, в основном, эстетическую ценность, поскольку
их наличие практически не сказывается на результатах вычислительного анализа).
Работу фильтров на реальных сигналах иллюстрирует
рис. 4.37, где приведена запись энцефалограммы и результаты ее фильтрации
фильтрами нижних и верхних частот по методам Фурье-преобразования и Баттерворта.
Так, в результате применения ФВЧ Баттерворта (канал 3) заметно пропускание
низкочастотных составляющих (в данном случае — высокоамплитудного 10-герцового
альфа-ритма) и существенные начальные искажения, а в результате применения
ФНЧ Баттерворта (канал 5) заметно искажение формы сигнала и сдвиг по фазе.
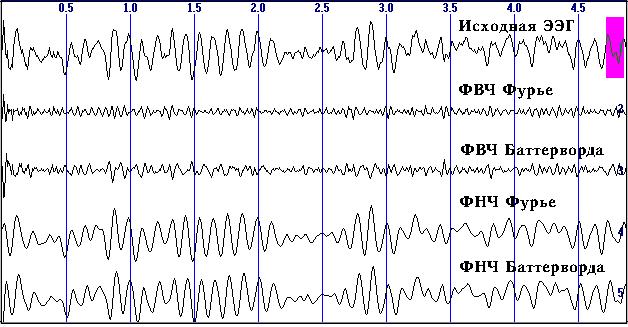
Рис. 4.37. Запись ЭЭГ (первый канал) и результаты
фильтрации ФВЧ (каналы 2, 3) и ФНЧ (каналы 4, 5) с частотой среза 15 Гц
по методу Фурье-преобразования (каналы 2, 4) и фильтром Баттерворда 3-го
порядка (каналы 3, 5)
Следует отметить, что данный метод неприменим в режиме
реального времени, поскольку он требует накопления значительного временного
интервала реализации сигнала и обладает недостаточным быстродействием при
больших частотах оцифровки. Видимо поэтому на его принципиальные преимущества
ранее не обращалось внимание.
Огибающаяпредставляет
собой положительно определенную функцию, которая в некотором смысле «огибает»
положительные и инвертированные негативные колебания сигнала (рис. 4.38,
б).
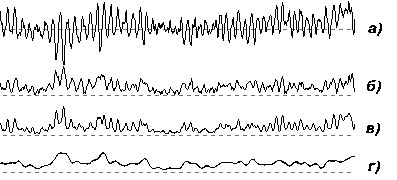
Рис. 4.38. Иллюстрация огибающей:
а — исходный сигнал; б — огибающая;
в
— абсолютная величина сигнала с 10 сглаживаниями; в — огибающая
после удаления низких частот
Математически огибающая определяется как модуль аналитической
функции (комплекснозначной), действительная часть которой равна сигналу,
а мнимая часть получена из действительной преобразованием Гильберта. В
свою очередь преобразование Гильберта может быть реализовано двукратным
преобразованием Фурье, когда перед обратным преобразованием спектр сдвигается
по фазе на 90°. Близкий к огибающей результат может быть получен взятием
абсолютного значения сигнала и несколькими сглаживаниями результата (рис.
4.38, в).
Огибающая может быть полезна при анализе быстроменяющихся
периодических сигналов благодаря следующим своим свойствам: 1) площадь
под участком огибающей представляет мощность сигнала на этом участке; 2)
после фильтрации с удалением высоких частот (рис. 4.38, г) огибающая
отражает изменение амплитудной модуляции сигнала, которая далее может быть
исследована средствами спектрального или периодометрического анализа.
Сглаживание
обычно применяется как эквивалент фильтрации для удаления из сигналов и
их спектров высокочастотных колебаний (шумов, наводок). Наиболее эффективен
метод параболического сглаживания скользящим средним по трем точкам, когда
амплитуды сигнала преобразуются по формуле:
xi+1= (xi+2xi+1+xi+2)/4,
i=1—n-2. (4.17)
При необходимости такая процедура сглаживания может
выполняться многократно. Примеры сглаживания: рис. 4.37, г — применительно
к ЭЭГ; рис. 4.19, в и рис. 4.23, б — применительно к спектрам
ЭЭГ.
Нормопатологическая классификация
ЭЭГ
Метод нормопатологической классификации ЭЭГ ставит
своей целью дать словесное заключение по основным характеристикам ЭЭГ-активности.
Его основы были заложены в 1965 г. работами Е.А. Жирмунской на основе обобщения
обширнейшего клинического материала (описание метода см. в [7]). В середине
90-х А.Я. Капланом был предложен ряд уточнений по вычислительным критериям
этого метода. С этими уточнениями метод обычно и реализуется.
Исходным материалом для анализа является запись
ЭЭГ, выполненная по восьми отведениям F3, F4, C3, C4, P3, P4, O1, O2 на
стандартную пробу «закрытые глаза» в течение 1 ми-нуты. Для анализа запись
разбивается на 30 эпох анализа по 2 секунды каж-дая. По каждой эпохе проводится
спектральный анализ и периодометрический анализ в четырех частотных диапазонах:
дельта, тета, альфа и бета-1. По результатам анализа в словесной форме
оцениваются следующие компоненты ЭЭГ-активности:
1. Степень нарушения ЭЭГ: 1) не определена; 2) норма; 3) легкая;
4) умеренная; 5) значительная; 6) грубая; 7) очень грубая.
2. Главные компоненты ЭЭГ: 1) бета-активность; 2) альфа-активность;
3) тета-активность; 4) дельта-активность; 5) смешанная; с амплитудой: а)
очень низкая; б) низкая; в) средняя; г) высокая; д) очень высокая.
3. Характеристика альфа-активности: 1) отсутствует; 2) одиночные
волны; 3) редкие группы волн; 4) хорошо представлена: а) регулярная по
частоте, модулированная; б) регулярная по частоте, без модуляции; в) слегка
дезорганизованная; г) заметно дезорганизованная; д) резко дезорганизованная;
5) зональные различия: а) не определены; б) хорошие; в) слегка сглаженные;
г) сильно сглаженные/извращенные.
4. Оценка бета-1 активности: 1) нет; 2) мало; 3) много; 4) очень
много.
5. Оценка медленноволновой активности: 1) практически отсутствует;
2) тета-активность выражена: а) слабо; б) умеренно; в) сильно; 3) дельта-активность
выражена: а) слабо; б) умеренно; в) сильно.
6. Очаговые изменения ЭЭГ (по частотным диапазонам и отведениям):
депрессия, активность, асимметрия.
Со времени своего опубликования метод продемонстрировал
высокую эффективность в качестве средства первичной экспресс-диагностики
и сравнимых по значимости альтернативных разработок в этом направлении
не появилось.
Трехмерная локализация ЭЭГ-источников
Трехмерная локализация ЭЭГ-источников ставит своей
целью поиск областей активности в глубинных структурах головного мозга.
Исходная гипотеза состоит в том, что именно активностью таких центров и
создается наблюдаемая на скальпе картина распределения различных ЭЭГ-показателей
(в этом качестве может фигурировать любой из показателей, перечисленных
на рис. 4.14, а также амплитуды вызванных потенциалов). Действительно,
стволовые и подкорковые центры является теми узловыми пунктами, через которые
проходит к коре вся афферентная иннервация. С другой стороны, неисчислимые
нервные пути связывают каждый такой центр со всеми областями коры головного
мозга. Этот эффект существенно усиливается за счет объемного проведения
потенциала в жидкостной среде мозга от источника до скальпа.
Рис. 4.39. Дипольная модель ЭЭГ-источников
Другое предположение состоит в том, что корковые
проекции активности нервного центра могут быть смоделированы посредством
дипольных источников, имеющих два полюса позитивного и негативного узконаправленного
излучения (рис. 4.39). Одной из предпосылок к такой модели является то,
что диполем можно смоделировать сразу и позитивную и негативную активность,
наблюдаемую в ЭЭГ. Другая предпосылка состоит в том, что электрически активные
области мозговых структур обычно включают достаточно близко расположенные
позитивный и негативный полюса.
Вычисление распределения ЭЭГ-источников производится
численным итерационным методом пошагового приближения. Исходными данными
для моделирования являются: а) картина распределения на скальпе избранного
ЭЭГ-показателя в конкретный момент времени; б) число дипольных источников;
г) желаемая точность приближения, определяющая окончание вычислений.
Поясним кратко процедуру вычислений. Положение
диполя в пространстве определяется шестью параметрами: тремя линейными
координатами, двумя угловыми и величиной дипольного момента. В начале распределение
диполей может быть выбрано произвольно. Далее начинается пошаговое изменение
одного из параметров одного диполя таким образом и до тех пор, пока не
будет достигнута максимальная точность совпадения картины проекции излучения
диполя на скальп и наблюдаемой картины. Затем этот же процесс повторяется
по оставшимся пяти параметрам данного диполя и так по всем диполям. После
этого вся процедура итерационно повторяется до достижения желаемой точности
совпадения проекции дипольных излучений и наблюдаемой картины. Несмотря
на большой объем вычислений, весь процесс на гигагерцовом процессоре занимает
считанные мгновения.
Существует несколько подходов к дипольному моделированию.
Хронологически первым (в России), наиболее проработанным, обоснованным
и экспериментально верифицированным следует признать подход В.В. Гнездицкого
и Ю.М. Коптелова [6], который позднее был реализован в известном пакете
BrainLoc. На данный подход ориентированы и большинство отечественных аналогов.
Результаты моделирования средствами BrainLoc
были верифицированы многими исследователями на больных с различного типа
патогенными внутримозговыми образованиями (опухоли, инсульты, травмы, воспаления).
Полученные распределения дипольных источников качественно находились в
согласии с томографическими картинами локализации подобного типа образований.
Тем самым этот метод может служить альтернативным и недорогим в сравнении
с томографией средством локализации очагов патологической ЭЭГ-активности.
Однако в обосновании метода недостает всесторонней статистической и количественной
верификации, которая могла бы ответить на следующие вопросы: а) каково
среднее отклонение центра и размеров облака распределения дипольных источников
от действительной локализации паталогических образований; б) каковы вероятностные
распределения этих отклонений; в) какие ЭЭГ-показатели и в каких случаях
наиболее адекватны в плане достоверной локализации.
Однако преимущества метода могут проявляться
и в совершенно другом направлении, если его рассматривать просто как средство
сжатия информации. Действительно, в результате его применения мы свертываем
систему множественных отведений до единственного показателя — локализации
фокуса ЭЭГ–источников. А это позволяет искать параметрические критерии
дифференциации различных функциональных состояний и заболеваний.
Сегментный анализ
ЭЭГ по своей природе является глобально нестационарным
процессом, применение методов частотного и корреляционного анализа к которому
связаны с принципиальными ограничениями и не позволяют надежно идентифицировать
различные функциональные состояния, личностные особенности и психические
заболевания. Поэтому в последние годы внимание многих исследователей привлекает
парадигма кусочно-стационарной структуры ЭЭГ, исходя из которой запись
ЭЭГ структурируется на сегменты относительной стационарности (для альфа-ритма,
например, от 0,1 до нескольких секунд) и ищутся критерии аутентичности
таких сегментных структур с целью дифференциации различных состояний.
Главным концептуальным достижением сегментационного
подхода явилось неожиданно открывшаяся исследователям довольно четкая временная
структурированность ЭЭГ, гораздо более тонкая, чем обычные генерализованные
перестройки ритмических компонентов, типа синхронизации-десинхронизации.
Тем самым предположение об организации ЭЭГ-сигнала из ограниченного набора
элементарных паттернов (Remond, 1972 г.) нашло свое косвенное подтверждение
.
Первоначально в этой области разрабатывались
методы так называемого параметрического оценивания, в частности авторегрессионной
сегментации, которая состоит в следующем. Выбирается скользящее окно заданной
ширины, в котором строится авторегрессионная модель ЭЭГ-процесса. Параметры
начальной модели-эталона сравниваются с параметрами модели для непрерывно
движущегося по ЭЭГ окна. Как только рассогласование достигнет установленного
порога, этот момент времени фиксируется как граница сегмента стационарности,
и в качестве эталона рассчитывается новая модель по следующему участку
ЭЭГ. Последующая классификация таких сегментов по спектрально–корреляционным
признакам завершает кусочно–стационарное описание ЭЭГ.
Однако высокая нестационарность ЭЭГ-сигнала не
позволяет построить достаточно надежную его математическую модель. Новая
технология непараметрической сегментации, связанная с поиском так называемых
«разладок» во временных рядах, не требует предварительного построения ма-тематической
модели процесса. Одним из подходов здесь является статистическое оценивание
участков, разделенных движущейся по ЭЭГ границей. Как только статистические
различия достигают заданного уровня, соответствующая временная точка фиксируется
как граница сегмента.
Другое направление состоит в использовании огибающей
ЭЭГ, по которой выделяются сегменты увеличения и уменьшения амплитуды колебаний
в избранном частотном диапазоне. Далее такая сегментация используется для
оценки синхронности подобных амплитудных изменений между различными парами
отведений, что в свою очередь может служить инструментом для выявления
конкретных межгрупповых различий [23-25].
Современным обобщением такого рода исследований
явился поиск в записях ЭЭГ устойчивых топографических паттернов или характерных
распределений значений избранного показателя по скальпу . В качестве таких
показателей могут выступать как амплитудные оценки в отведениях, так и
оценки синхронности между парами отведений. При таком подходе длительная
запись ЭЭГ разбивается на короткие и перекрывающие друг друга во времени
эпохи, на которых и вычисляются значения избранного показателя, распределение
которого по скальпу дает локальную топографическую карту. Среди полученного
множества карт устойчивые топограыические паттерны выделяются по критерию
высокой коррелированности карт. Для выделения классификации таких паттернов
используются методы многомерной статистики: факторный, кластерный и дискрими-нантный
анализ. Далее выделенные паттерны могут быть использованы для выявления
конкретных межгрупповых различий [Dietrich Lehmann.
Brain Electric Microstates and Cognition: The Atoms of Thought. In E. R.
John et al. (eds.), Machinery of the Mind. Springer Science+Business Media
New York 1990].
Заключение
В случае типовых клинических исследований неврологу
в плане частотного анализа ЭЭГ можно дать достаточно четкие рекомендации:
расположите монополярные отведения по системе 10—20%: приведите пациента
в расслабленно–спокойное состояние с закрытыми глазами, установите частоту
ЭЭГ–регистрации 128—256 Гц на интервале 1—5 мин, проанализируйте 5—10–секундные
интервалы по амплитудам спектра в основных частотных диапазонах и получите
удовлетворительные и сравнимые результаты.
В случае же научных исследований ситуация кардинально
усложняется существованием неизмеримого множества нетиповых и неклинических
постановок задач и целей, необходимостью исследования как быстротечных,
так и медленных процессов, а также их причинных, пространственных и временных
взаимосвязей и т. п. Поэтому научному исследователю ЭЭГ с необходимостью
следует знать и рефлекторно чувствовать основные особенности ее измерительно–вычислительных
инструментов, причем нередко более глубоко для своей области, чем сами
создатели методов — профессиональные математики. Некоторые из таких насущных
и малоизвестных особенностей и были рассмотрены в данном разделе.
Литература
5. Гнездицкий В.В. Вызванные потенциалы мозга в клинической практике.
Таганрог: Медиком, 1997.
6. Гнездицкий В.В. Обратная задача ЭЭГ и клиническая электроэнцефалография.
Таганрог: Медиком, 2000
7. Жирмунская Е.А. Клиническая электроэнцефалография. М.: 1991.
13. Макс Ж. Методика и техника обработки сигналов при технических
измерениях. М.: Мир, 1983.
17. Отнес Р., Эноксон Л. Прикладной анализ временных рядов. М.:
Мир, 1982. Т. 1, 2.
20. Рандалл Р.Б. Частотный анализ. Брюль и Къер, 1989.
22. Русинов В.С., Гриндель О.М., Болдырева Г.Н., Вакер Е.М. Биопотенциалы
головного мозга. Математический анализ. М.: Медицина, 1987.
23. Каплан А.Я. Проблема сегментного описания электроэнцефалограммы
человека//Физиология человека. 1999. Т.25. №1.
25. Каплан А.Я. Нестационарность ЭЭГ: методологический и экспериментальный
анализ//Успехи физиологических наук. 1998. Т.29. №3.
29. Frederic J Harris. Use of windows for harmonic analysis. IEEE
proceedings. 1978. 66—1.
38. Кулаичев А.П. Некоторые методические проблемы частотного анализа
ЭЭГ//Журнал ВНД. 1997. № 5.
43. Кулаичев А.П. Методология автоматизации психофизиологических
экспериментов/сб. Моделирование и анализ данных. М.: РУСАВИА, 2004.
44. Кулаичев А.П. Компьютерная электрофизиология и функциональная
диагностика. Изд. 4-е. М.:ФОРУМ – ИНФРА-М, 2007, 2016. 640 с.
47. Кулаичев А.П. Об информативности когерентного анализа в исследо-ваниях
ЭЭГ, Журн.высш.нерв.деят. 2009. 59(6): 757-767.
49. Кулаичев А.П. Метод анализа корреляционной синхронности ЭЭГ
и его возможности Журн.высш.нерв.деят. 2011. 61(4): 485-498.
50. Кулаичев А.П. Сравнительный анализ корреляционной синхронности
и амплитудных соотношений ЭЭГ в ночном сне Журн.высш.нерв.деят. 2012. 62(1):
108-119.
52. Кулаичев А.П., ГорбачевскаяН.Л., ГорюновА.В.,
СорокинА.Б., Хромов А.И. Различия показателей синхронности биоэлектрической
актив-ности ЭЭГ у здоровых и больных шизофренией детей и подростков. Журн.
неврол. и психиатр. им. С.С.Корсакова. 2012. 12: 55-62.
53. KulaichevA.P., Gorbachevskaya N.L. Differentiation
of Norm and Disorders of Schizophrenic Spectrum by Analysis of EEG Correlation
Synchrony. J.Exp.Integr.Med., 2013. 3(4):267-278.
54. Кулаичев А.П., Изнак А.Ф., Изнак Е.В., Корнилов В.В., Сорокин
С.А. Изменения корреляционной синхронности ЭЭГ при депрессивных рас-стройствах
психогенного типа. Журн.высш.нервн.деят., 2014, 64(2):1-9.






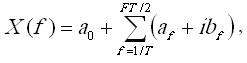 (4.1)
(4.1)













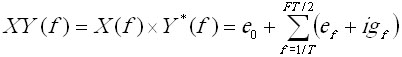 ,
(4.3)
,
(4.3)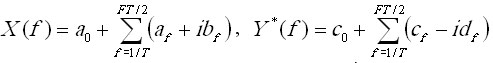 , и выполняя
почастотное умножение компонент X(f), Y*(f) с
выделением действительных и мнимых составляющих результата получаем выражения
для составляющих кросс-спектра:
, и выполняя
почастотное умножение компонент X(f), Y*(f) с
выделением действительных и мнимых составляющих результата получаем выражения
для составляющих кросс-спектра:
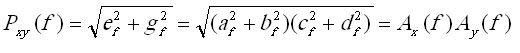 (4.4)
(4.4)


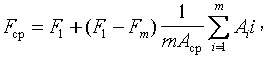 (4.13)
(4.13)
 (4.7)
(4.7)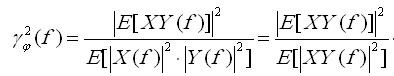 (4.8)
(4.8)


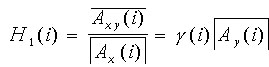 .
(4.11)
.
(4.11)

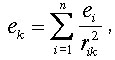 ,
(4.14)
,
(4.14)
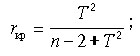 (4.16)
(4.16)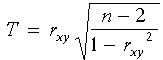 — статистика Стьюдента
с n–2 степенями свободы.
— статистика Стьюдента
с n–2 степенями свободы.










![]()