 Закономерности гравитационного
коллапса - существуют ли черные дыры?
Закономерности гравитационного
коллапса - существуют ли черные дыры?
г
Кулаичев А.П., 2012-2017
ссылки при цитировании на публикации:
Кулаичев
А.П. Оценка вариационного размаха показателей временной динамики гравитационного
коллапса в метрике Шварцшильда. Акт пробл гум и ест наук, №6-2, 2017 и
Кулаичев
А.П. Временная динамика гравитационного коллапса. ВИНИТИ, №260-В2014,
2014г.
 Аннотация.В
работе рассмотрена базовая модель центрально-симметричного невозмущенного
коллапса. Показано, что образование черной дыры является крайне скоротечным
процессом длительностью 1.42-2.45с для звезд допустимого диапазона масс
3-450 от солнечной. Вследствие квантового ограничения на расстояние до
горизонта событий h=(r-rg)/rg
коллапс завершается практически одновременно по часам удаленного и сопутствующего
наблюдателей, различие между ними составляет 0.008-0.858с. Длительность
релятивистской стадии коллапса, присущей только образованию черной дыры,
когда координатное время начинает возрастать линейно в зависимости от ln(h)
при h<0.1, составляет 0.0013-0.175с. Образование горизонта событий
является не моментальным явлением, а процессом увеличения радиуса горизонта
из зародыша квантовых размеров до окончательной величины rg,
протекающим спустя 0.78-1.34с после начала коллапса и длительностью 0.64-1.1с.
В связи с этим ньютоновские и релятивистские стадии коллапса сферических
областей различного объема и плотности перекрывают друг друга, что не позволяет
инструментально отличить коллапс с образованием черной дыры от коллапса
с образованием нейтронной звезды, заканчивающегося до релятивистской стадии
при h=2-3 .При падении на черную дыру любой элементарной частицы
горизонт событий увеличивается настолько, что и для удаленного наблюдателя
частица оказывается внутри горизонта. Для черных дыр размером rg>3
мкм увеличение массы за счет поглощения реликтового излучения превышает
потерю массы вследствие излучения Хокинга, для черных дыр звездного происхождения
поглощение превышает излучение более чем в 1030 раз.
Аннотация.В
работе рассмотрена базовая модель центрально-симметричного невозмущенного
коллапса. Показано, что образование черной дыры является крайне скоротечным
процессом длительностью 1.42-2.45с для звезд допустимого диапазона масс
3-450 от солнечной. Вследствие квантового ограничения на расстояние до
горизонта событий h=(r-rg)/rg
коллапс завершается практически одновременно по часам удаленного и сопутствующего
наблюдателей, различие между ними составляет 0.008-0.858с. Длительность
релятивистской стадии коллапса, присущей только образованию черной дыры,
когда координатное время начинает возрастать линейно в зависимости от ln(h)
при h<0.1, составляет 0.0013-0.175с. Образование горизонта событий
является не моментальным явлением, а процессом увеличения радиуса горизонта
из зародыша квантовых размеров до окончательной величины rg,
протекающим спустя 0.78-1.34с после начала коллапса и длительностью 0.64-1.1с.
В связи с этим ньютоновские и релятивистские стадии коллапса сферических
областей различного объема и плотности перекрывают друг друга, что не позволяет
инструментально отличить коллапс с образованием черной дыры от коллапса
с образованием нейтронной звезды, заканчивающегося до релятивистской стадии
при h=2-3 .При падении на черную дыру любой элементарной частицы
горизонт событий увеличивается настолько, что и для удаленного наблюдателя
частица оказывается внутри горизонта. Для черных дыр размером rg>3
мкм увеличение массы за счет поглощения реликтового излучения превышает
потерю массы вследствие излучения Хокинга, для черных дыр звездного происхождения
поглощение превышает излучение более чем в 1030 раз.
Introduction.Collapse
with formation of a black hole is very swift-passing process about 2-3
seconds for stars of any valid mass and due to quantum constraints. Its
duration, due to quantum constraints for the distance to event horizon,
is almost the same for accompanying and remote observers so the difference
between them is less than one second. The duration of the relativistic
phase of collapse, when it begins to increase linearly dependent on logarithm
of distance to the event horizon, does not exceed tenths of a second. The
formation of event horizon is not an instantaneous phenomenon but it stretchs
out in time by increasing of its radius from the quantum embryo having
duration less then one second. For an external observer, a black hole appears
as point object with non-zero event horizon surface, which in its boundary
layer of quantum thickness "freezes" the gravitational mass of collapsar.
Newtonian and relativistic phases of collapse of different spherical
areas are overlaped that does not allow by instrumental measurements to
distinguish collapse with the formation of neutron star from collapse with
the formation of black hole.

1. ВВЕДЕНИЕ
Вопросы по озаглавленной
теме продолжают волновать интересующуюся наукой общественность, вызывая
многочисленные и порой очень острые обсуждения в университетских и научно-ориентированных
форумах (corum.mephist.ru, astronomy.ru/forum, astronet.ru, dxdy.ru, e-science.ru/forum,
scientific.ru/dforum и др.).

а)
|

б)
|
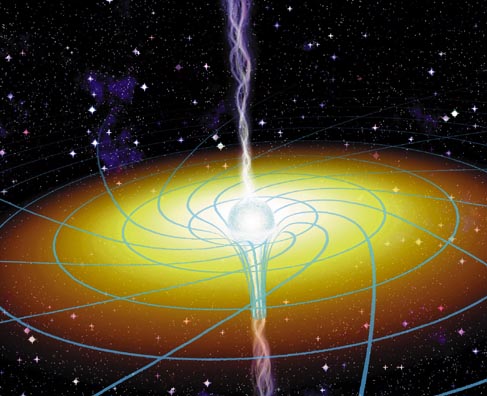
Рис. 1. Художественные иллюстрации: а)
черная дыра, окруженная аккреционным диском; б)
центральная черная дыра в далекой галактике, которая
не видна сквозь плотный тор, состоящий из вращающегося молекулярного газа
и пыли
В фундаментальных
источниках подобные вопросы излагаются преимущественно чисто теоретически.
Например, в классической монографии [1], где рассматривается гравитационный
коллапс сферического тела, приводится формула (обозначенная там 102.5)
координатного времени коллапса (времени по часам удаленного наблюдателя):
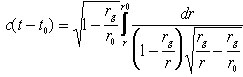 .
(1)
.
(1)
r0 — радиус условной поверхности звезды в момент начала
коллапса t0;
rg=2MG /c2 — гравитационный радиус
или горизонт событий, MG — произведение массы звезды на гравитационную
постоянную;
с — скорость света.
Собственное
время коллапса (по часам падающего тела) определяется там же формулой (102.8):
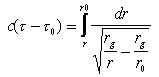 .
(2)
.
(2)
Подобное
мы читаем и в другой фундаментальной монографии [2]: «Итак, по часам далекого
неподвижного наблюдателя время достижения rg всегда равно бесконечности»,
и далее: «То, что бесконечно во времени внешнего наблюдателя, конечно по
часам падающего. Можно ли привести более наглядную иллюстрацию относительности
понятия временной бесконечности?»
Эти заключения переносятся физиками–теоретиками
и в свои научно?популярные произведения [3]: «Для него (внешнего наблюдателя)
поверхность звезды лишь за бесконечно долгое время приближается к сфере
Шварцшильда, как бы застывая на гравитационном радиусе. Поэтому раньше
черные дыры называли еще застывшими звездами».
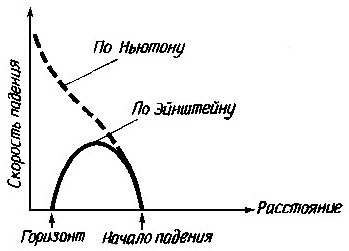
В еще
более популярных источниках [4, 5] эти выводы иллюстрируются простыми и
вроде бы понятными, но безразмерными графиками, подобными рис. 2, имеющими
крайне далекое отношение к действительности.
а)
|
б)
|
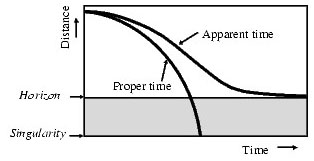
Рис. 2. Популярные иллюстрации динамики
коллапса: а) скорость коллапса.
Удаленный наблюдатель видит, что скорость коллапса замедляется до нуля
по мере того, как оно приближается к горизонту событий; б)
наблюдаемое
(apparent) и собственное (proper) время (time) коллапса в зависимости от
расстояния (distance) до горизонта событий (horizon) и центра черной дыры
(singularity)
Отсюда у многих читателей возникают резонные вопросы: сейчас так много
говорят о наблюдениях черных дыр, как звездной массы, так и сверхмассивных
в центрах галактик, но как же мы можем их наблюдать, когда время их коллапса
для нас бесконечно? Так можно ли считать черные дыры действительно существующими
для нас? Кроме того, в чисто теоретическом плане остаются непроясненными
важные моменты: 1) какова детальная динамика коллапса во временном и пространственном
измерениях; 2) насколько эта динамика различается для звезд разных масс;
3) является ли образование горизонта событий моментальным событием или
процессом, протяженным во времени; 4) существуют ли физические ограничения
на теоретическую временную бесконечность коллапса.
2. ТЕОРЕТИЧЕСКИЕ ОСНОВАНИЯ
Прежде,
чем перейти к рассмотрению этих вопросам, сделаем еще несколько формальных
уточнений.
Рассмотрим коллапс в центрально-симметричном гравитационном поле с метрикой
Шварцшильда (цитируем [3, С. 386]: «Итак, несмотря на то, что гравитационное
поле вращающейся звезды отличается от поля Шварцшильда, ее коллапс качественно
протекает так же, как и у невращающейся»):
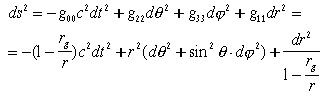 .
(3)
.
(3)dr=dx*kg
, dt=dt/kg,
(4)
где 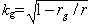 — коэффициент гравитационного изменения масштабов, kg®0
при r®rg.
— коэффициент гравитационного изменения масштабов, kg®0
при r®rg.
Иными словами, при приближении к rg
временные интервалы dt в сопутствующей
системе отсчета нам представляются удлиняющимися (время замедляется), а
линейные размеры dx укорачиваются, то есть пространство как бы сжимается
для нас при приближении к rg (рис. 3).
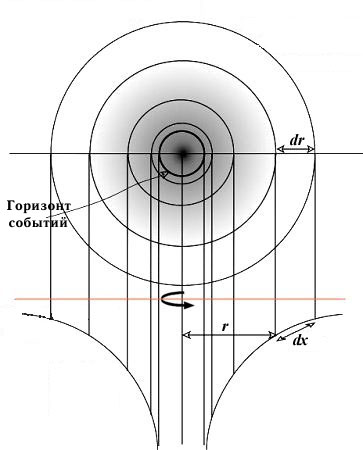
Рис. 3. «Сжатие» пространства вблизи черной
дыры: одинаковые интервалы для сопутствующего наблюдателя dx представляются
все более укороченными dr для внешнего наблюдателя
В метрике (3)
координатная скорость падения определяется выражением (3.5.1) из [2]:
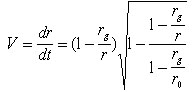 ,
(5)
,
(5)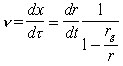 .
(6)
.
(6)
Однако в гравитационном
поле две системы отсчета не эквивалентны, в отличие от эквивалентности
двух инерционных систем в СТО. Если для удаленного наблюдателя время в
сопутствующей системе замедляется, то для сопутствующего наблюдателя время
в удаленной Вселенной ускоряется, и при достижении им горизонта событий
Вселенная за бесконечное время перестанет существовать.
Приливные
силы. При приближении к горизонту событий
чудовищно возрастает градиент напряженности гравитационного поля, и любое
тело будет разорвано на атомы приливными силами. Путь имеется небольшая
черная дыра звездного происхождения с rg=104
м, к которой на расстояние 1 м приблизилось тело, размером с человека 1.5
м, когда голова находится на расстоянии 2.5 м от rg.
Ускорение свободного падения в гравитационном поле определяется выражением:
Подставляя сюда значения
r
= 10001 и 10002.5 м, получаем чудовищную разность ускорений, действующих
на ноги и голову: Dg=1.654*1014 м/с2,
и столь же чудовищную разрывную силу. По этой причине популярный миф о
путешествиях через кротовые норы в другие Вселенные не имеет оснований.
РАСЧЕТ ДИНАМИКИ КОЛЛАПСА
Вернемся теперь
к нашему основному вопросу. Для ответа на него необходимо детально рассчитать
динамику коллапса: как изменяются его скорость, длительность и другие характеристики
при r®rg с точки зрения
двух систем отсчета. Здесь-то и можно получить неизвестные широкой аудитории
и отсутствующие в популярной литературе ответы на вопрос: как и где конкретно
интеграл (1) расходится?
Возьмем в качестве
начальных условий минимально подходящую для коллапса звезду в три солнечных
массы с r0 =1000000 км и rg =10 км.
Для вычислений показателей динамики коллапса можно использовать формулы
(1,2,5,6), хотя они и выведены для свободно падающей в вакууме частицы.
Однако, цитируем по [18, с.409]: «после сколь–нибудь заметного отхода
(звезды) от состояния равновесия силы тяготения уже на конечную величину
превышают силы давления и ускорение сжатия составляет конечную долю ускорения
свободного падения. Таким образом, очень быстро после «срыва» звезда сжимается
практически с ускорением свободного падения, и силы давления не играют
существенной роли в динамике коллапса».
При использовании
формул (1,2) расчет может проводиться методом численного интегрирования
с кусочно-линейной аппроксимацией и пропорциональным уменьшением шага Dr
в области возрастания нелинейности подынтегральных выражений. Такое численное
моделирование вполне по силам студентам ряда технических и физико-математических
специальностей. Однако это неизбежно приводит к накоплению в той или иной
степени погрешности вычислений, поэтому предпочтительнее получить и использовать
выражения интегралов (1,2) в явном виде (такое преобразование интегралов
вполне по силам любому студенту, успешно сдавшему экзамен по математическому
анализу на первом курсу вуза):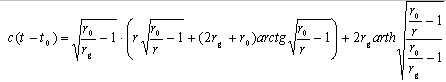 (7)
(7)
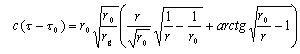 (8)
(8)
То, что подобные
формулы не были известны ранее и их видовое разнообразие иллюстрирует показательная
цитата из [9]: “Даже для случая радиального движения интегрировать здесь
нелегко, как это видно из полученного сложного выражения [приводится ссылка
на неопубликованные расчеты N.Khuri, 1957 г.]”. Тем не менее, наши аналитические
выкладки показали, что большинство подобных формул совпадает с выражениями
(7,8) с точностью до преобразований. Это подтверждают и результаты наших
числовых расчетов по различным формулам.
Более того,
ни одна из упомянутых формул не использована авторами для расчета основных
динамических характеристик коллапса и границ их вариабельности в зависимости
от массы коллапсара.
3. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Возьмем в качестве начальных
условий минимально подходящую для коллапса звезду массой в три солнечных
на завершающей стадии ее эволюции. В образовании нейтронной звезды или
черной дыры участвует преимущественно область ядра, а внешняя оболочка
рассеивается в пространстве в результате мощных пульсаций звезды или сверхвзрыва.
Положим, что ядро на этой стадии имеет размер не более белого карлика,
что отвечает начальным значениям r0=9000 км (с учетом
r0=6371
км белого карлика в случае Солнца) и rg=10 км. Избранные
результаты расчетов приведены в табл.1, где использованы следующие обозначения:
h=(r–rg)/rg
—
высота условной поверхности звезды над горизонтом событий;
V=dr/dt — наблюдаемая (координатная)
скорость коллапса;
u=dr/dt
— собственная скорость коллапса;
Dt=t–t0
— наблюдаемая длительность коллапса;
Dt=t–t0
— собственная длительность коллапса.
Таблица 1. Изменение показателей
гравитационного коллапса
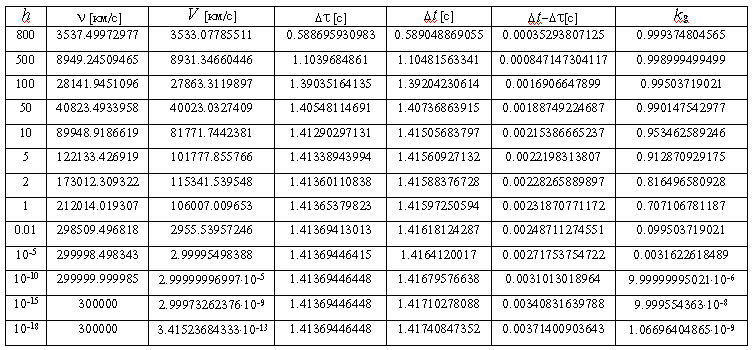
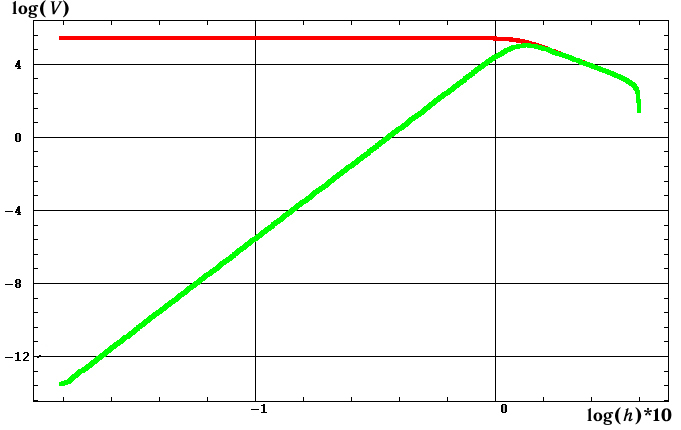
На рис. 4а
по этим данным приведены графики изменения собственной и координатной скорости
коллапса. Как можно заметить, эти графики никоим образом не напоминают
популярную их интерпретацию на рис. 2а. Собственная скорость
коллапса u начинает приближаться к скорости
света при h<10 км, то есть на удалении порядка одного гравитационного
радиуса. Здесь же начинают сказываться и эффекты гравитационного изменения
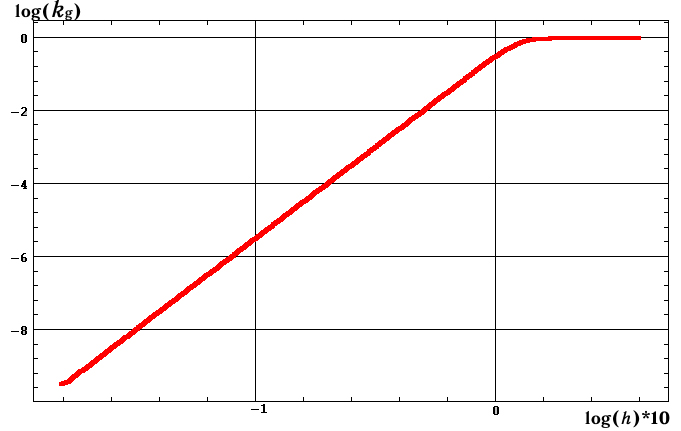
масштабов (рис. 8) kg=0.707.
Координатная
скорость коллапса V достигает своего максимума при r=3rg
(это соотношение выполняется для любых начальных условий, то есть для любой
массы коллапсирующей звезды), где ее значение составляет V=115468.9
км/с (более трети от скорости света). Далее V начинает уменьшаться
по закону, приближающемуся к линейному V=с/rg*(r–rg),
что определено влиянием уменьшения kg (графики V
на рис.4а и kg на рис.4б имеют идентичную
тенденцию при h<1 км). Однако значение V продолжает более
чем на порядок превосходить расстояние, оставшееся до гравитационного радиуса.
Иными словами, если V вдруг в любой момент перестало бы уменьшаться,
то тело достигло бы rg за 1/10 секунды.
а)
|
б)
|
Рис.4. Динамические характеристики коллапса
в зависимости от высоты условной поверхности звезды над горизонтом событий
h=r–rg
(масштабы
по обеим осям логарифмические):
а) собственная
(зеленая кривая) и координатная (красная кривая) скорости коллапса ; б)
значения
коэффициента гравитационного изменения масштабов kg
3.1. ОБЩАЯ ДЛИТЕЛЬНОСТЬ КОЛЛАПСА
Рассмотрим далее динамику суммарной длительности
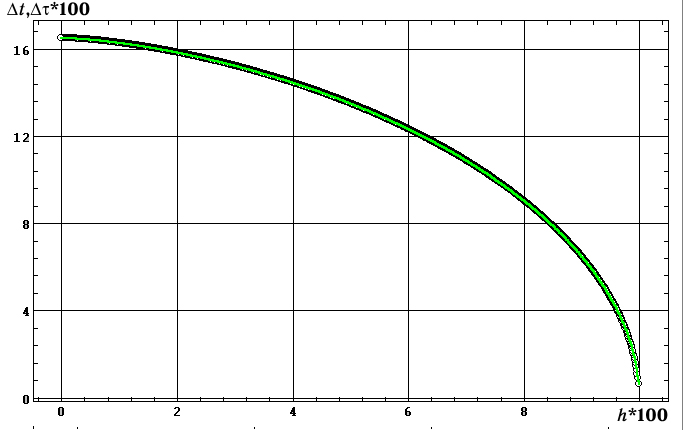
коллапса. Если использовать натуральные масштабы по осям (рис. 5а),
то собственное и координатное время коллапса визуально не различается вплоть
до h=r–rg®0,
что совершенно не соответствует популярной интерпретации этого процесса
на рис. 2б. Показательно, что рис. 2б воспроизводится без существенных
изменений и во многих фундаментальных монографиях, например [9, 10]. Это
показывает, что подобные иллюстрации были подготовлены исходя только из
авторских интуитивных представлений о математических свойствах теоретических
уравнений, но не на основе точных вычислений. Поэтому неизвестно кем порожденная
легенда о бесконечном времени коллапса по часам удаленного наблюдателя
продолжает до сих пор кочевать не только по фундаментальным работам, но
и по университетским аудиториям и умам бесчисленных потребителей научно-популярной
информации.
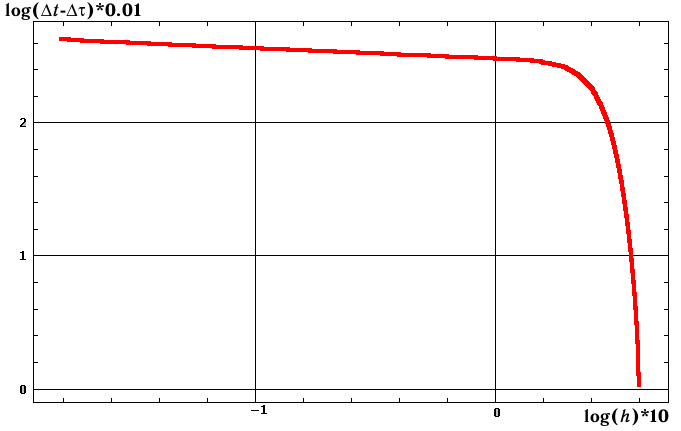
Чтобы понять природу такого драматического
несоответствия, построим график изменения разности между координатным и
собственным временем коллапса Dt–Dt
в зависимости от логарифма h (рис. 5б).
а)
|
б)
|
Рис.5. Временные характеристики коллапса:
а)
изменение
собственного (зеленое) и координатного (черное) времени коллапса в зависимости
от h=r–rg; б)
изменение
разности между координатным и собственным временами коллапса Dt–Dt
в зависимости от log10(r–rg)
Из графика рис.
5б видно, что основная величина разности между собственным и координатным
временем коллапса образуется на интервале до r=10rg
и составляет Dt–Dt=0.024778
секунды или менее 0.00015% от величины Dt. При
r<2rg
увеличение этой разности начинает подчиняться логарифмическому закону:
Dt–Dt
= 0.02489–7.679*10-5log10(r–rg)
с очень малым коэффициентом при логарифме от r–rg.
Отметим, что этот результат подтверждает вышецитируемое как бы мимолетное
и второстепенное замечание из [1] о приближении к гравитационному радиусу
по экспоненциальному закону с очень малым характерным временем ~rg/с,
что в нашем примере дословно означает: оставшееся расстояние до rg
каждый раз сокращается в 2.718 раз за одну 30-тысячную долю секунды или
же за 1 секунду оно сокращается в 1013000 раз. Расчетная величина
коэффициента при десятичном логарифме практически совпадает с rg/с:
10/300000*ln(10)=-7.675*10-5.
3.2. СТАДИИ КОЛЛАПСА
Тем самым во временной динамике коллапса
можно выделить три стадии:
1) на первой ньютоновской стадии до h>10, kg>0.95
сжатие звезды происходит в хорошем соответствии с классической теорией
тяготения;
2) вторая стадия до h>0.1, kg>0.09
является переходной;
3) на третьей релятивистской стадии h<0.1, kg<0.09
показатели временной динамики коллапса изменяются в соответствии с логарифмической
зависимостью от (r-rg)/rg
согласно уравнениям теории тяготения Эйнштейна.
Следует особо подчеркнуть, что зависимость
рис.5б является универсальной, и для звезд различной массы изменения касаются
только масштаба вертикальной оси.
Яркость излучения коллапсара I
и его частота излучения w изменяются как [4]: I=const* ((r-rg)/r)4,
w=const*
(r-rg)/r.
При h<0.1 яркость излучения коллапсара составляет 4.67*10-9
от исходной, а частота излучения составляет 0.0083 от исходной, то есть
задолго до релятивистской стадии коллапсар становится астрономически не
наблюдаемым.
По приведенной
логарифмической формуле можно прогнозировать последующее развитие событий:
h=r–rg = lP=10-38-38
км (lP – Планковская длина), Dt–Dt
= 0.02781 с;
h=10-1000lP,
Dt–Dt
= 0.1016 с;
h=10-1000000lP,
Dt–Dt
= 76.77 с.
Вернемся
к вопросу о несоответствии рис.5б и рис. 2б, который воспроизводится без
принципиальных изменений и во многих фундаментальных монографиях и статьях
[6,10-13]. Однако все подобные графики иллюстрируют не реальную динамику
коллапса поверхности звезды, начинающегося с удаления r0~103rg,
а условный пример падения пробной частицы на черную дыру, начинающегося
с r0=3rg .
Тем самым
этот процесс, начинающийся там, где для нашего примера должно заканчиваться
образование нейтронной звезды, протекает в области больших гравитационных
искажений, так в диапазоне r=3-1.01rg коэффициент
изменения масштабов kg= 0.82-0.1. За счет этого графики
собственного и координатного времени визуально расходятся и при r=1.01rg
(т.е. к началу релятивистской стадии) разность составляет Dt–Dt
= 0.000555-0.000247 = 0.000308 с. Этот чисто визуальный эффект якобы подтверждает
легенду о временной бесконечности коллапса для удаленного наблюдателя.
Однако и в
данном случае при r-rg = lPl
получаем Dt =0.0033 с, Dt–Dt
= 0.00307 с, то есть имеет место не бесконечный, а практически моментальный
по своей скоротечности процесс. Якобы быстро уходящий во временную бесконечность
и теряющийся у оси времени хвост релятивистской стадии на рис.2б имеет
тот же самый мизерный временной наклон -7.648*10-5*log10(r-rg).
3.3. КВАНТОВЫЕ ОГРАНИЧЕНИЯ
Как нетрудно
заметить, выше приведенные последние два прогноза относятся к чисто математической
абстракции, поскольку на расстояниях до горизонта событий, меньших Планковской
длины
lP, дальнейшее непрерывное движение невозможно,
а возможны только бесконечные осцилляции к гравитационному радиусу и обратно.
Действительно, будут лишены физического смысла утверждения, подобные следующему:
падающее тело менее чем за 77 секунд проходит 0.999…(1 миллион девяток)
часть от расстояния
lP, оставшегося до горизонта событий,
а движение в завершающей 10-1000000 части от lP
занимает бесконечное время по часам удаленного наблюдателя.
Поскольку
физические процессы коллапсирующего тела протекают в сопутствующей системе
отсчета, то lP следует пересчитать в масштабе, наблюдаемом
из координатной системы отсчета согласно выражения dr = dx*kg
решением уравнения 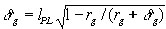 , в результате
чего получаем для рассмотренного примера drg=lP2/rg=10-77
км, тогда Dt–Dt(drg)=0.00837
с или 0.5% от Dt. Таким образом, физически коллапс
заканчивается за Dt =1.664 с, а длительность
релятивистской стадии составляет 0.006 с или 0.36% от Dt.
, в результате
чего получаем для рассмотренного примера drg=lP2/rg=10-77
км, тогда Dt–Dt(drg)=0.00837
с или 0.5% от Dt. Таким образом, физически коллапс
заканчивается за Dt =1.664 с, а длительность
релятивистской стадии составляет 0.006 с или 0.36% от Dt.
Одной
из немногих теоретических работ, обсуждающих подобные результаты, является
[6], где в §9.1 рассматривается роль квантовых эффектов в физике черных
дыр, цитируем: «Для сферической черной дыры с массой М величина
«дрожания» drg имеет следующий
вид: drg~lP2/rg
. Интересно отметить, что хотя эта величина мала для обсуждаемых нами черных
дыр с М>>mP, само существование этого эффекта
качественно меняет идеализированное классическое описание коллапса тела
или падения частиц в черную дыру с точки зрения удаленного наблюдателя.
Вместо формально бесконечного выражения: 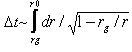 для длительности этих процессов по часам удаленного наблюдателя следует
ожидать появления конечной величины ~rgln (rg/lP)
в результате замены rg на rg+drg
в нижнем пределе интегрирования» .
для длительности этих процессов по часам удаленного наблюдателя следует
ожидать появления конечной величины ~rgln (rg/lP)
в результате замены rg на rg+drg
в нижнем пределе интегрирования» .
3.4. УНИВЕРСАЛЬНОСТЬ ЗАКОНОМЕРНОСТЕЙ
Рассмотренные закономерности приложимы
к коллапсарам любой допустимой массы. При этом следует учитывать, что в
процессе коллапса участвует преимущественно плотное ядро звезды с размерами,
не превышающими белого карлика. Внешняя же оболочка рассеивается в пространстве
за счет пульсации звезды на исходе ее существования или в результате сверхвзрыва.
Для нашего примера с начальными условиями r0=9000
км, rg=10 км получаем Dt(drg)
= 1.422 с, Dt–Dt(drg)=0.008246
с или 0.58% от Dt,
длительность релятивистской стадии коллапса составляет 0.0013 с.
Для одной из самых массивных
звезд ближнего галактического окружения, красного сверхгиганта Бетельгейзе
при начальных условиях r0=16000
км, rg=45 км получаем Dt(drg)
= 1.613 с, Dt–Dt(drg)=
0.03315 с или 2.06% от Dt,
длительность релятивистской стадии коллапса составляет 0.0265 с.
Для коллапсара максимально
допустимой массы в 450 солнечных в предположении его начальной плотности,
соответствующей средней плотности белого карлика, имеем начальные условия
r0=50000
км, rg=1350 км, при которых
получаем Dt (drg)
= 2.449 с, Dt–Dt(drg)=
0.8584 с или 35% от Dt,
длительность релятивистской стадии коллапса 0.1749 с.
Таким образом, в диапазоне
допустимом для коллапсара масс от 3 до 450 солнечных основные временные
показатели изменяются незначительно по величине Dt(drg)
= 1.422-2.449 с, Dt–Dt(drg)
= 0.008246-0.8584 с, длительность релятивистской стадии коллапса 0.0013-0.1749
с.
Рассмотрим теперь процесс падения
на черную дыру rg=10 км
материальной частицы с орбиты Земли r0=150000000
км. В этом случае получаем Dt(drg)
= 3041834 с = 35.21 дней, Dt–Dt(drg)=
0.3101 с, длительность релятивистской стадии составляет 0.00138 с. Отсюда,
в частности, следует, что все окружающей пространство очищается от частиц,
не имеющих стабильных орбит, за мизерные по астрономическим масштабам сроки.
Это ставит под сомнение часто встречающееся предположение о том, что черные
дыры окружены плотными и протяженными аккреционными дисками.
3.5. ДИНАМИКА ФОРМИРОВАНИЯ ЧЕРНОЙ ДЫРЫ
Вместе с тем, реальная динамика гравитационного
коллапса может быть сложнее рассмотренного идеализированного случая. Так
само образование черной дыры определенно является не одномоментным событием
в завершение общего коллапса, что определено наличием градиента плотности
в коллапсаре от периферии к центру. В связи с этим каждой сферической области
коллапсара начального радиуса r0i
соответствует собственный горизонт событий rg(r0i)
и собственное время его достижения Dt(r0i).
При этом время Dt(r0i)
увеличивается с увеличение объема или радиуса r0i
сферической области. Поэтому более объемные области отстают по времени
от нижерасположенных в достижении соответствующих им rg(r0i).
В качестве начального приближения
положим, что начальная плотность в коллапсаре изменяется аналогично плотности
в ядре Солнца. Согласно стандартной модели Солнца [14] изменение его плотности
имеет вид:
r=519x4-1630x3+1844x2-889x+155
[г/см3],
(11)
где x - расстояние от центра x=0 до поверхности x=1
звезды. При этом распределение плотности в ядре x=0-0.25 (рис.6)
с высокой достоверностью (p<10-9)
соответствует квадратичной регрессионной модели:
r=153.6-830x+1268x2
(12)
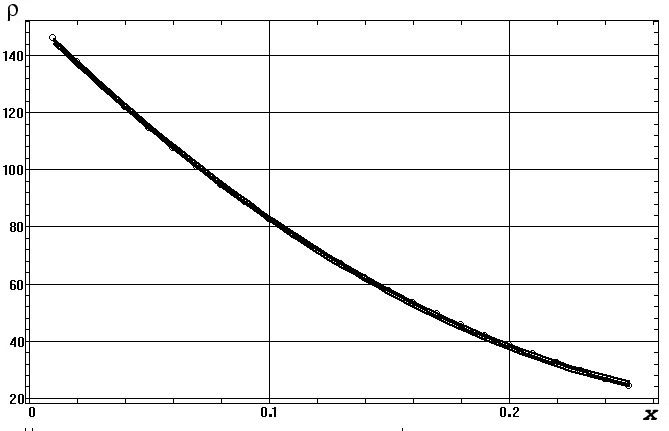
Рис.7. Изменение плотности r
[г/см3] в ядре Солнца x=0-0.25
Преобразуя зависимость (12) перенормировкой
на rmax=1
и xmax=1 для концентрических
сферических областей x=0-1 коллапсара массой в 3 солнечных произведем
следующие последовательные вычисления:
1) изменение массы центральной сферической области в ядре m(x)
как функции ее радиуса x =0-1;
2) изменение гравитационного радиуса rg(x)
[км], соответствующего m(x);
3) изменение координатного времени завершения коллапса Dt(x)
для сферических областей r0=9000x
[км] по формуле (7) с учетом drg
*10-77 км.
В результате полученная зависимость Dt(x)
с высокой достоверностью (p<10-9)
соответствует квадратичной регрессионной модели:
Dt(x)=0.7777+0.3508x+0.2847x2.
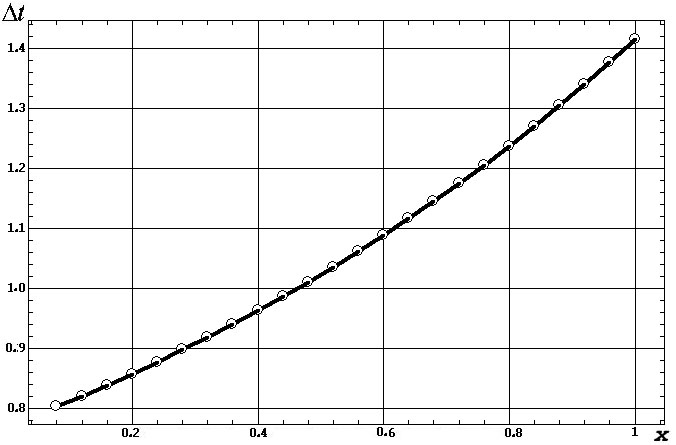
Рис.8. Изменение координатного времени Dt
образования и роста черной дыры в зависимости от относительного радиуса
сферической области x=0-1 коллапсара
Отсюда процесс образования и роста
черной дыры (рис.8) начнется (x=0) с образования зародыша квантового
размера спустя 0.7777 секунды после начала коллапса ядра звезды и завершается
(x=1) через 1.4166 с достижением горизонтом событий своего окончательного
размера rg(1). Для звезды
максимальной массы в 450 солнечных образование черной дыры начинается спустя
1.342 секунды после начала коллапса ядра звезды и завершается через 1.096
с.
В процессе рассмотренного, распределенного
во времени формирования черной дыры индивидуальные релятивистские стадии
внутренних областей, накладываются на ньютоновские стадии областей большего
размера, теряя тем самым свою физическую уникальность для внешнего наблюдателя.
В плане астрофизических наблюдений
важно отметить, что для звезд с начальной массой менее трех солнечных гравитационный
коллапс может приводить к образованию нейтронной звезды с радиусом порядка
2-3 от гравитационного rg,
то есть такой процесс заканчивается до достижения релятивистской стадии.
Тем самым релятивистская стадия является единственным отличием этих двух
видов коллапса, а ее скоротечность и наличие эффектов наложения во времени
различных стадий делает проблематичным ее инструментальное обнаружение.
Здесь следует также отметить термингоризонт
видимости, появившейся и закрепившемся в публикациях с начала 80-х
годов [9, 16, 17]. Он трактуется как динамический эквивалент (в процессе
коллапса) горизонта событий, который, в свою очередь, обозначает статическое
завершенное состояние черной дыры (поэтому вышерассмотренный процесс роста
черной дыры можно было бы трактовать как образование и увеличение горизонта
видимости). Однако из всех атрибутов горизонта событий в отношении горизонта
видимости обычно выделяется только одно: падающие на него по касательной
излучение начинает совершать круговое движение. В связи с накоплением такого
излучения у горизонта видимости якобы образуется огненная стена
(firewall).
Прежде всего, отметим, что в связи
со скоротечностью коллапса (менее 3 с) разделение этих двух понятий теряет
смысл, а firewall не успевает образоваться. С другой стороны, как показано
ниже, за счет поглощения реликтового излучения процесс роста черной дыры
никогда не прекращается, и в таком случае никогда не образуется завершенный
горизонт событий. Далее, поскольку при приближении любого кванта излучения
к rg на расстояние drg
(как это также показано ниже) квант оказывается за горизонтом событий,
то образование никакого firewall не возможно. Тем самым здесь мы имеем
пример дублирующего терминологического мифотворчества.
3.6. РОСТ ЧЕРНОЙ ДЫРЫ
В продолжение раздела 3.2 выясним, какая дополнительная
масса dm
должна сосредоточиться на расстоянии drg
от rg, чтобы rg
увеличился на drg.
Будем исходить из соотношения rg=1.483m*10-27
м. Тогда для drg=10-74
м получаем dm=
6.743*10-48 кГ, что в 7.4*1016
раз меньше массы электрона (9.1*10-31
кГ). Такой прирост массы соответствует падению на черную дыру одиночного
фотона с энергией 6.07*10-31 Дж,
что по E=hc/l
соответствует излучению с длиной волны l=3.275*105
м при длине волны максимума мощности реликтового радиоизлучения (1.9 мм).
Таким образом, при падении
на черную дыру любой одиночной элементарной частицы, горизонт событий увеличивается
настолько, что частица оказывается внутри горизонта.
При плотности реликтового излучения
r=4.005*10-14
Дж/м3 в сфере радиуса c
содержится E=4/3rpc3=1.13*1026
Дж энергии. Поскольку это излучение распространяется во все стороны, то
падающий на расположенную в центре этой сферы поверхность черной дыры радиуса
rg
поток энергии составляет часть энергии Е или мощность Pcmb
в
соотношении поверхностей с радиусами rg
и c, а именно Pcmb=Erg2/c2=5.03*10-5rg2
Дж/с. Отсюда для черной дыры минимальной звездной массы rg=104
м поток энергии реликтового излучения составляет 5.03*103
Дж или в пересчете на увеличение массы черной дыры m=E/c2=5.59*10-14
кГ/с, что эквивалентно поглощению 3.347*1013
атомов водорода в секунду m(H)=1.67*10-27
кГ. Для черной дыры, образовавшейся из звезды максимально допустимой массы
в 450 солнечных с rg=1350
км, все приведенные оценки увеличиваются в 1.823*104
раз.
3.7. ИЗЛУЧЕНИЕ ХОКИНГА
В 1973 году один из крупнейших современных
физиков Стивен Хокинг посетил Москву, где Яков Зельдович и Алексей Старобинский
продемонстрировали ему, что в соответствии с принципом неопределённости
квантовой механики вращающиеся чёрные дыры должны порождать и излучать
частицы (ранее такое предположение было высказано Владимиром Грибовым).
Хокинг ухватился за эту идею и в следующем году в журнале Nature опубликовал
свою знаменитую статью. Сущность этого явления состоит в следующем.
В квантовой теории поля физический
вакуум наполнен постоян-но рождающимися и исчезающими флуктуациями различных
полей ( «виртуальными частицами»). В поле внешних сил динамика этих флуктуаций
меняется, и если силы достаточно велики, прямо из вакуума могут рождаться
пары частица-античастица. Такие про-цессы происходят и вблизи (но всё же
снаружи) горизонта событий чёрной дыры. При этом возможно, что одна из
частиц (не важно какая) падает внутрь чёрной дыры, а другая улетает и доступна
для наблюдения. Из закона сохранения энергии следует, что такая «упавшая»
за горизонт событий частица из рождённой виртуальной пары должна обладать
отрицательной энергией, так как «улетевшая» частица, доступная для удалённого
наблюдателя, обладает положительной энергией.
В дальнейшем это явления получило
название «излучение Хокинга», и по его интерпретации черные дыры должны
постоянно испаряться вплоть до полного своего исчезновения. Однако при
этом не учитывалось соотношение мощностей поглощения и излучения.
Мощность излучения Хокинга равна РHwk=hс6/(7680G2m2).
Подставляя значения констант и переходя от массы к гравитационному радиусу,
получаем РHwk=7.875*10-22/rg2
Дж/с. Для состояния равновесия эту мощность следует приравнять вышеприведенной
мощности поглощаемого реликтового излучения Pcmb=5.03*10-5*rg2
Дж/с. Отсюда можно найти равновесное значение гравитационного радиуса rg=6.29*10-5
м, что соответствует массе черной дыры m=4.181*1022
кГ, сопоставимой с массой Луны. Тем самым, черные дыры размером rg>0.0629
мм только за счет поглощения реликтового излучения постоянно увеличивают
свою массу и объем, включая все объекты звездного происхождения с rg>104
м.
Отношение Pcmb
к РHwk для черной дыры звездного
происхождения и минимального размера rg=104
м равно 1.556*1033, что соответствует
отношению массы всех планет Солнечной системы (2.638*1027
кг) к массе одной песчинки (2*10-6
кг). Может ли такая «песчинка» вылететь из черной дыры, если на
нее ежесекундно обрушивается масса всех планет Солнечной системы?
Отметим также, что черные дыры поглощают
еще и космический фон реликтовых электронных нейтрино с массой порядка
35 эВ, а также поток космических лучей. Плотность этого фона составляет
1.5*10-8 нейтрино/м3 или 8.4*10-10
Дж/м3, что в 2.1*104
раз превосходит энергетическую плотность реликтового радиоизлучения. Однако
точная оценка мощности этого излучения, поглощаемого черной дырой, невозможна
в связи с невозможностью определить среднюю скорость реликтовых нейтрино.
Таким образом, в существующей Вселенной
влияние выдающегося открытия Хокинга исчезающее мало или же вообще полностью
отсутствует.
ЗАКЛЮЧЕНИЕ
В работе рассмотрена базовая модель центрально-симметричного
невозмущенного гравитационного коллапса. Однако для большинства других
моделей, использующих те или иные предположения о влиянии факторов вращения,
электрического заряда, трения, давления, фазовых переходов в состоянии
вещества и т.п., будут с некотыми численными вариациями воспроизводиться
пять основных выводов из настоящего исследования.
1. С чисто математической точки
зрения временная длительность коллапса в координатной системе отсчета является
бесконечной. Однако, вследствие квантового ограничения на расстояние до
горизонта событий коллапс звезд любой массы заканчивается практически одновременно
как по собственному, так и по координатному времени в течение 1.422-2.449
с, а различия между ними составляют 0.58-36% от общей длительности коллапса.
2. Длительность релятивистской
фазы коллапса, когда координатное время начинает возрастать линейно в зависимости
от логарифма расстояния до горизонта событий при r-rg<0.1rg,
составляет 0.0013-0.1749 с. Крайняя скоротечность этой стадии и присутствие
эффектов наложения релятивистских и ньютоновских стадий для сферических
областей возрастающего объема и массы делает проблематичным инструментальное
обнаружение релятивистской фазы, позволяющее отличить коллапс с образованием
нейтронной звезды от коллапса с образованием черной дыры.
3. Образование горизонта событий
является не моментальным явлением, а процессом увеличения его радиуса из
зародыша квантовых размеров до окончательной величины rg
с
длительностью 0.6355-1.098с.
4. При падении на черную дыру любой
элементарной частицы, горизонт событий увеличивается настолько, что для
удаленного наблюдателя частица оказывается внутри горизонта.
5. Черные дыры размером rg>3
мкм только за счет поглощения реликтового излучения постоянно увеличивают
свою массу и размер, для черных дыр звездного происхождения поглощение
реликтового фона превышает излучение Хокинга более чем в 1030
раз.
По частным результатам, не представленных
в известных публикациях, следует отметить: а) детальный расчет динамики
коллапса для звезд допустимого диапазона масс, включая координатные и сопутствующие
измерения; б) выделение трех стадий коллапса: ньютоновская, переходная
и релятивистская; в) расчет временной динамики формирования горизонта событий;
г) практическое отсутствие различий по всем показателям коллапса для звезд
любой массы в сопоставлении с длительностью типичных астрономических процессов.
См. также:
О
соотношении гравитационного и релятивистского изменения пространственных
и временных интервалов
Об отношении научных
журналов к данной работе
ЛИТЕРАТУРА
1. Ландау Л. Д., Лившиц Е.М. Теоретическая
физика. Т. 2, Теория поля. М.: Наука. 1988.
2. Зельдович Я. Б., Новиков И. Д.
Теория тяготения и эволюция звезд. М: Наука, 1971.
3. Новиков И. Черные дыры и Вселенная.
М.: Мол. гвардия, 1985.
4. Кауфман Уильям Дж. Космические рубежи
теории относительности. М: МИР, 1981.
5. Luminet Jean-Pierre. Black Holes.
Cambridge University Press, 1992 (русский перевод http://www.astronet.ru/db/msg/1180633).
6. Новиков И. Д., Фролов В.П.
Физика черных дыр. М: Наука, 1986.
7. Альберт Эйнтейн. Собрание научных
трудов. Т.1, Работы по теории относительности 1905-1920. М: Наука, 1965.
8. Логунов А.А. Релятивистская теория
гравитации. М.: Наука, 2006.
9. Рис М., Руффини Р. Чёрные дыры,
гравитационные волны и космология. (М: Мир, 1977) – перевод с англ.: Martin
Rees, Remo Ruffini and John Archibald Wheeler. Black holes, gravitational
waves and cosmology (N.Y., 1974).
10. Шапиро С., Тьюколски С. Черные
дыры, белые карлики и нейтронные звезды. Физика компактных объектов. Т.2
(М: Мир, 1985) – перевод с англ.: Stuart L. Shapiro, Saul A. Teukilsky.
Black
holes, white dwarfs and neutron stars (N.Y., 1984).
11. Чандрасекар С. Математическая теория
черных дыр (М.: Мир, 1986) [Chandrasekhar S. The mathematical theory
of black holes. (Oxford, N.Y., 1983)].
12. Мизнер Ч., Торн К., Уилер Дж. Гравитация,
Т.2 (М.: Мир, 1977) [Misner C.W., Thorne K.S., Wheeler J.A. Gravitation.
V.2 (San Francisco, 1973)].
13. Гриб А.А., Павлов Ю.В. Возможно
ли увидеть бесконечное будущее Вселенной при падении в черную дыру? УФН.
179:279-283, 2009.
14. Turck-Chieze S., Lopes I. Toward
a unified classical model of the Sun: on the sensitivity of neutrinos and
helioseismology to the microscopic physics Astrophys. J. 408:347-367, 1993.
15. Zeeya Merali. Stephen Hawking:
'There are no black holes'. Nature news. 24 January 2015
16. ШацкuйА.А., АндреевА.Ю. Динамика
образования горизонта событий. ЖЭТФ (116)2:353-368, 1999.
17. Merali Zeeya. Stephen Hawking:
'There are no black holes' // Nature news. 24 January 2015.
18. Зельдович Я.Б., Новиков И.Д. Релятивисткая
астрофизика // УФН. 1964. №3. С. 377–417.
19. Michael Kesden, Shravan Hanasoge.
Transient solar oscillations driven by primordial black holes. Phys. Rev.
Lett. (107)11:111–115. 2011.
ПОСЛЕСЛОВИЕ
За рамками нашего исследования остались еще и
другие «белые пятна на черных дырах», вызывающие вопросы у аудитории и
ждущие своего научного и популярного прояснения, в частности:
-
Считается, что существует большой класс вращающихся
черных дыр с особыми свойствами. Но как черная дыра может вращаться, когда
время на ее поверхности для внешнего наблюдателя останавливается и никакое
движение невозможно? Не может же быть, чтобы время останавливалось в радиальном
направлении, но продолжало бы себе преспокойно течь в тангенциальном направлении?!
-
Обычно черные дыры изображаются в центре плотного
и вращающегося облака межзвездного газа (рис. 1). Но посмотрим на нашу
солнечную систему: 1) за 4-5 миллиардов лет солнечный ветер вымел весь
подобный газ далеко за пределы нашей системы; 2) в результате взрыва сверхновой,
сопровождающий коллапс, несравнимо более мощное "выметание" произойдет
и с более крупными образованиями. Так откуда же образоваться аккреционному
диску вокруг черной дыры?
-
Пусть некий путешественник направляется к «кротовой
норе». Но когда он достигнет гравитационного радиуса, в удаленной Вселенной
пройдет бесконечное время, галактики и звезды исчезнут, и что тогда будет
с одинокой черной дырой в несуществующей Вселенной?
-
Вот путешественник пересек горизонт событий, но
вся масса черной звезды уже давно ушла в сингулярность, то есть в точку
невозврата. И будет ли эта безмерная точка для путешественника продолжать
существовать и создавать эффекты гравитационного искривления пространства-времени?
-
Решения уравнений Эйнштейна непрерывно продолжаются
за гравитационный радиус вплоть до центральной сингулярности. Какие есть
физические основания для такого математического продолжения решений уравнений,
выведенных для внешнего, несингулярного состояния, ведь уже на гравитационном
радиусе сила тяготения и искривление пространства-времени становятся бесконечными?
-
За горизонтом событий временная координата преобразуется
в пространственную и наоборот. Что же будет тогда с наблюдателем, пересекшим
гравитационный радиус, когда радиальное пространственное измерение его
тела стало временем? Как он будет продолжать падать дальше к центру гравитационной
сингулярности? И где, в каких координатах будет находиться этот центр?




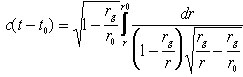 .
(1)
.
(1)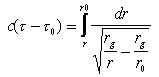 .
(2)
.
(2)

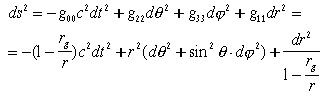 .
(3)
.
(3)
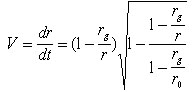 ,
(5)
,
(5)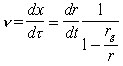 .
(6)
.
(6)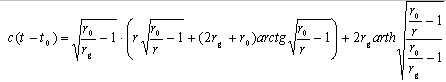 (7)
(7)
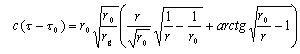 (8)
(8)




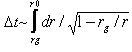 для длительности этих процессов по часам удаленного наблюдателя следует
ожидать появления конечной величины ~rgln (rg/lP)
в результате замены rg на rg+drg
в нижнем пределе интегрирования» .
для длительности этих процессов по часам удаленного наблюдателя следует
ожидать появления конечной величины ~rgln (rg/lP)
в результате замены rg на rg+drg
в нижнем пределе интегрирования» .
