The Informativeness of Coherence Analysis in EEG Studies
ã A. P. Kulaichev.
source: Neuroscience and Behavioral Physiology, 41(3): 321-328, 2011

     Abstract. Numerous methodological and computational errors typical of coherence analysis of EEG recordings are discussed. Comprehensive review of the fundamental disadvantages of coherence functions shows that this measure cannot be regarded as a reliable and effective indicator of the synchronicity of EEG processes.
     Keyworgs: coherence, spectral analysis, EEG non-stationarity, amplitude modulation

     The first application of mathematical methods into electroencephalography is traditionally associated with N. Viner, who proposed the use of correlation analysis in 1936, taking the EEG to be a stationary wave process. The intensive application of mathematical methods charac-terized the first stage in the development of computerized electrophysiology [6, pp. 20–32]. This was taken up by physiologists and the engineers working with them with great enthusiasm. However, professional mathematicians, who do not see any great scientific prestige from immersing themselves deeply in this field, generally restrict themselves to overall theoretical positions expressed in general terms. The introduction of mathematical methods by technical specialists led to the diffusion of a wide range of incorrect and even erroneous methods, viewpoints, and concepts among physiologists. In particular, the two fundamental dif-ferences between EEG signals and most other physical signals are not considered: a) fundamental non-stationarity; b) amplitude modulation at all frequency ranges. This applies to a particularly critical extent to coherence analysis, to which attention has been drawn previously [5].

     Sources. According to [7, p. 138], “Goodman first proposed the so-called coherence function in 1960 [15] and studies reported in [14] its first use in the analysis of brain bioelectrical activity.” On the one hand, studies in [15] did not consider or mention coherence, while spectral analysis methods had been developed long before this and were resumed in basic monographs from well known authors such as Barlett (1955), Bendat (1958), Blackman and Tewkey (1959), and others. On the other hand, the coherence for-mula as applied to electrophysiology was introduced and commented on (without source references) by one of the authors of [14] in later studies [17].
     It should also be noted that the extensive specialist literature on coherence has a number of deficiencies. Thus, the coherence function for processes x(t) and y(t) (some-times termed coherence squared) is usually stated as:

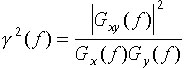,                 (1)
where |Gxy(f)| is the modulus of the complex-valued cross spectrum, and Gx(f) and Gy(f) are the power spectra of pro-cesses x(t) and y(t).
     Most sources [1, p. 146; 7, p. 138; 10, p. 342; 13, p. 36; 17, p. 172], apart from citing Equation (1), which gives a value of unity, provide no elaboration. Only a few mono-graphs [11, p. 271] clarify that the numerator and denomi-nator are averaged for the ensemble (averaged spectra cal-culated for sequential analysis epochs). However, nowhere is it stated which of the several possible types of averaging should be used in Equation (1).
     Subsequently, after first defining Equation (1) on p. 146 in [1], it was repeated many times in the text, though the need for averaging across the ensemble is explained (and then quite indirectly) only in a special addendum of terms on p. 517. An even more confused situation is found in [2]: on p. 138 of volume 2, i.e., long after Equation (1) on p. 112, the discussion of smoother evaluations of coherence makes reference to correlational and spectral windows on p. 294 of volume 1, which in turn refers to the previous description (p. 289) of the Bartlett smoothing method. In [9, p. 463], there is an analogous coherence equation, whose numerator is defined by a previous Fourier transformation from a correlational function with an erroneous reference to chapter 3, though it is in fact defined in chapter 4, p. 43, using averaging over a time interval, which should also be recognized as a very confused way of explaining the need for the numerator of Equation (1) to include complex-valued averaging of the ensemble in a frequency range, which is far from obvious in relation to matching of the results. In [10, p. 330], the unquoted coherence Equation (1) is given immediately after exposition of various methods of averag-ing spectra, including averaging using a sliding frequency window (the Daniel method [10, p. 322]), which creates the false illusion that this averaging can also be applied to cal-culating coherence. It remains possible that calculation of this “pseudocoherence” has been used. Furthermore, most specialist monographs make wide use of mathematical computation in an integral form, far from real cases of time-limited and sampled signals.
     With respect to this confused situation, there is a need for a brief discussion of the basic mathematical relationships using a much simplified example.

     Mathematical definitions. Let there be two monoharmonic and centered processes with some frequency f:

x(t)=acos2pft+bsin2pft; y(t)=ccos2pft+dsin2pft .   (2)
     If a whole number of the periods of these processes fall within an analysis epoch, then the coefficients a, b, c, and d will be (in complex-valued spectra X(f), Y(f)) the real and imaginary parts of the discrete Fourier transform (DFT) for frequency f
X(f)=a+ib; Y(f)=c+id,  (3)
where i is the imaginary term.
     The power spectra of these processes are the squares of the moduli of X(f) and Y(f), i.e., the squares of their ampli-tude spectra Ax(f), Ay(f):
Gx(f) = Ax(f)2 = a2+b2;  Gy(f) = Ay(f)2 = c2+d2,   (4).
and the phase spectra are given by
jx(f) = arctg(b/a); jy(f) = arctg(d/c).    (5)
     We note that on the complex plane, any spectral component, for example X(f), is represented by a vector whose length is defined by the modulus |X(f)| and the angular position by the phase ?x(f), its components a and b being the projections of the vector onto the real and imaginary axes.
     The complex-valued cross spectrum of processes x(t), y(t) is defined by
Gxy(f)=e+ig ,     (6)
where Gxy(f)=e+ig ,  ãäå e=ac+bd, g=bc–ad.
        The modulus of the cross spectrum is given by the product of the amplitude spectra of the two processes
,  (7)
and its phase spectrum is given by the difference between the phase spectra of the two processes
jxy(f) = arctg(g/e) = jx(f)–jy(f).      (8)

        We will use E[...] to indicate the operation of averag-ing for the ensemble for nonoverlapping epochs (Bartlett method). One possible averaging formula for calculating the square of the coherence will then be of the form:

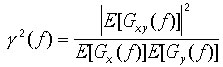,      (9)
where   .
     In relation to the vagueness noted above, it is of note that Equation (9) does not occur in the widely available literature.
     Discussion of the significance of coherence in EEG studies continues to the present day, for example in [16] (con-temporary “improvements” in coherence analysis require separate evaluation), where in contrast to Equation (1), as in the physiological primary source noted previously [17], a non-squared coherence formula is presented.

     Coherence in technical addenda. Methods for spectral analysis were initially used for signals of physical origin and were only later applied to EEG investigations. In technical addenda, coherence is used as a particularly second-degree characteristic – only for evaluating the significance of other cross-spectral characteristics and for defining measures of the influence on them of noise and/or nonlinearity. Decreases in coherence values can result from the following main causes [1, p. 179; 11. p. 271]:
1) presence of noncorrelating noises in signals determining instability in the phase of the cross spectrum over time;
2) the presence of nonlinear relationships between processes;
3) leakage of power determined by inadequate frequency resolution, i.e., observation periods of insufficient duration;
4) the presence of time delays on transfer of interactions between two pro-cesses commensurate with the observation interval.
     Small coherence values can indicate the insignificance, at the frequency being addressed, of other cross-spectral characteristics or can indicate the need to increase the num-ber of averagings to eliminate the effects of noise.
     The cardinal difference is that signals of physical origin often truly have stationary harmonics created by real sources: radio stations operating at their characteristic frequency; errors in the geometry of the moving part of a mechanism inducing vibration, etc. By recording the radio background at different locations at the frequency of a given radio station, we will at any time point have a fixed phase difference (determined by the distance of the measuringpoints from the source). If there is radio noise at this frequency, then the cross-phase of this harmonic will show some degree or other of change; coherence allows this vari-ability to be evaluated and increases in the number of averagings allow it to be decreased.
     In the brain there are actually no harmonic oscillators or anything producing stationary reflections in the EEG. Arbitrarily dividing the frequency band into spectral lines (defined by the duration of the analysis epoch), Fourier transformation yields pseudoharmonics as a result of interference between a multiplicity of uncontrolled and unknown factors, and these harmonics change from epoch to epoch. This is reflected primarily on instantaneous autospectra, where each harmonic does not have a smooth transition at the boundary of two neighboring analysis epochs, but rather sharp, random jumps in amplitude, and, consequently, in phase. These jumps are then reproduced in the cross-phase of the two processes and hence in coherence values.
     In summary, we can conclude that the large and unique value that coherence has acquired in EEG studies as compared with its background position in primary sources is ungrounded. Coherence was developed to solve other tasks and is based on other premises, so efforts should have been made to find and construct more appropriate and reliable measures at the very beginning of its EEG application.

     The needs of electrophysiology. In the physiology of higher nervous activity, it is important to have reliable assessments of different aspects of the synchronicity of EEG processes. When high synchronicity is present, the presence of different types of physiological relationships between processes can be proposed and verified: the effects of one process on the other, the influence of a common source on both processes, and detection of topographical patterns of highly synchronized relationships with the aim of differentiating functional states, personal characteristics, normal and pathological, the effects of drugs, etc.
     The attraction of coherence for these purposes appears largely to result from the repeatedly published and insufficiently discussed proposition that coherence in a frequency
range is an analog of the Pearson correlation coefficient over a time period [2, p. 112; 10, p. 342; 11, p. 270; 13, p. 36; 17, p. 172]. As will be shown twice, these propositions are quite far from reality. Here, in particular, we will note that a) coherence (Equation (1)) can relate only to the square of the correlation coefficient, which in practice is extremely rarely used; b) unlike coherence, the range of values of the correlation coefficient is from –1 to +1. Interpretation of coherence. Equation (9) does not give a direct and clear informative interpretation of coherence. We will therefore consider another acceptable version of Equation (1) [6, p. 196], whose denominator is a transformation using Equation (7):

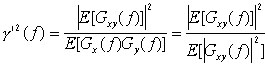,     (10)
which, to distinguish it from g2, we will henceforth term phase coherence (we note that this order of averaging comes from an illustration [11, p. 270] of the addition of cross-
spectrum vectors in the complex plane).
      This assessment is a good approximation to g2: a) the correlation between them in the range g2 = 0–1 is greater than 0.95; b) the mean difference between values is less than 0.074. In addition, evaluation of g’2 has a clear inter pretation [11, p. 270]: the numerator contains the geometric sum of the cross-spectrum vectors for sequential analysis epochs and the denominator contains the arithmetic sum of the vector lengths. Therefore, the more randomly the phase of the cross-spectrum changes, the smaller the numerator will be in comparison with the denominator. The more stable the cross-spectrum phase, the closer the numerator will be to the denominator. Thus, phase coherence is a better indicator of the stability/instability of the phase difference (Equation (8)) between two processes.
     g2 coherence partially inherits this property of reflecting synchronicity, but its significance depends not only on the stability of the phase difference between the two processes, but also on their amplitude stability, this being quite complex. Despite the equivalence of the denominators in Equations (9) and (10) in relation to Equation (7), they differ in terms of the order of averaging. Thus (as illustrated by the numerical example in Table 1), the denominator in Equation (9) decreases not proportionally to the numerator, but to progressively lesser extents, in response to increases in the amplitude variability of the processes; in this it contrasts with the denominator in Equation (10).
     Table 1 shows a simple example in which we consider two sequential epochs in processes x(t) and y(t) using three different amplitude ratios (versions 1–3). In all cases, epoch 2 shows a 90° phase change in the cross-spectrum (the autospectrum vectors of process x(t) are 0° and 90° in epochs 1 and 2, while the autospectrum vector of process
y(t) remains at 90° in both epochs). If the amplitudes of the processes are the same in both epochs (version 1), then both Equations (9) and (10) give the same result, g2 = g’2 = 0.5, which comprehensively reflects a jump of 90° in the phase difference between the processes at the two sequential epochs. When the amplitudes of the process are halved in
epoch 2 (version 2), we obtain g2 = 0.68, while a four-fold reduction (version 3) gives g2 = 0.889 (compared with the constant g’2 = 0.5).
TABLE 1. Relationship between Coherence and Amplitude-Phase Ratios of the Spectra of Two Monoharmonic Signals
     Thus, g2 coherence gives an increased assessment in relation to the extent of synchronicity of the processes, with a complex relationship with the extent of their amplitude variability. This coherence is fundamentally different from the correlation coefficient as a stable indicator of a linear relationship between two paired values which are not dependent on the ratio of the ranges of their values.
    As the amplitude of the spectral harmonics of EEG processes vary significantly even over short time periods, we can conclude that g2 coherence is a poor numerical indicator of the degree of synchronicity of EEG processes (we note that g’2 phase coherence is no better than g2 because of other errors as discussed below).

     Errors in spectral analysis. One of the main errors in discrete Fourier transformation (DFT) arises from leakage or drainage of power from spectral peaks to neighboring
spectral lines. In technical addenda, this is decreased by using a variety of correcting windows and this method has been  transported  uncritically  into electrophysiology. However, studies reported in [6, p. 200] showed that windows have a double effect on spectral peaks: they compress broad peaks but broaden well localized peaks. Therefore it is more correct to calculate the mean and maximum amplitudes of a spectrum after preliminary filtration of the signal in the range being analyzed, which excludes leakage and modulating peaks from neighboring ranges.
     However, the leakage effect depends on the ratio of the harmonic period and the analysis epoch [6, p. 200]: there is no leakage when there is a whole number of harmonic periods per analysis epoch and leakage is maximal when there is a half-integer number of harmonic periods per analysis epoch. Furthermore, even in the latter case, leakage decreases in inverse proportion to increases in distance from the main peak. However, there is a further, not previously noted, but important distortion to spectra, associated with the amplitude modulation present in all EEG signals. This effect [6, p. 187] results in the appearance of two symmetrical side peaks of 40% or more of the amplitude of the central peak and separated from it by a number of spectral lines equal to the number of signal modulation periods observed (this applies to monoharmonic signals, and the situation with real EEG traces will be significantly more complex).
     These two main errors produce additional (to the abovenoted) random fluctuations in spectra, which are par-ticularly clear visually when frequency resolution is high. Phase spectra are more subject to these fluctuations than amplitude spectra.

a)
b)
c)
d)
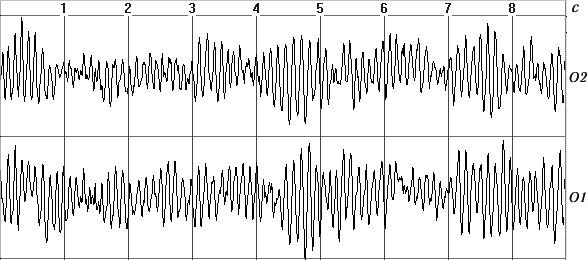
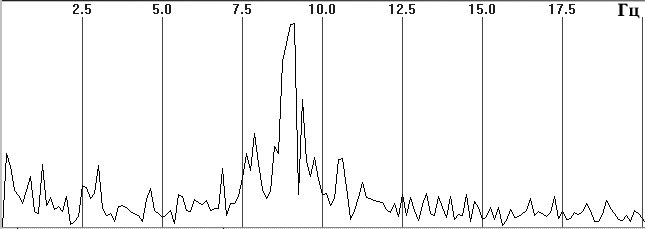
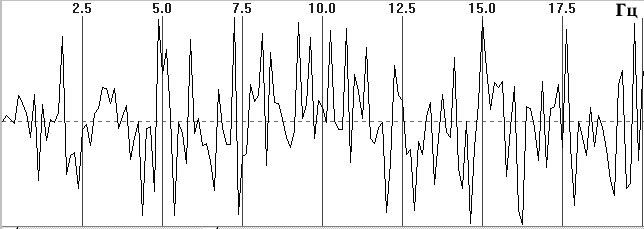
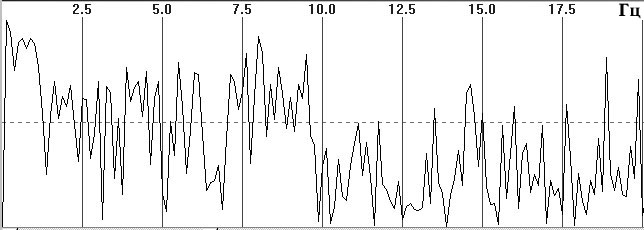
Fig. 1. Typical EEG spectra. a) Occipital EEG lead with a high alpha-rhythm content (9-sec trace), sampling frequency 128 Hz, analog filters with bandpass 0.5–32 Hz, total trace duration 64 sec; b) amplitude cross-spectrum (one 8-sec epoch); c) phase cross-spectrum (one 8-sec trace); d) coherence spectrum (average of 8 epochs).

     Figure 1, a shows a small fragment of a typical and prolonged EEG trace with a high alpha-rhythm content in the two occipital leads. Figure 1, b shows the amplitude cross-spectrum between these two processes for an 8-sec analysis epoch, which reveals a high-amplitude peak at the fundamental frequency of the alpha rhythm, 9 Hz. The presence of low-amplitude random fluctuations throughout the frequency range should also be noted. Figure 1, c, d shows the phase cross-spectrum and the coherence spectrum, which are already completely dominated by random fluctuations and no clear frequency pattern can be discriminated. Figure 2 shows a plot of changes in cross-spectrum phase at the fundamental alpha-rhythm frequency of 9 Hz for 32 sequential epochs. This shows that the phase (whose stabil-ity significantly reflects coherence) shows random and large epoch-by-epoch variations over the wide range ±160°. This randomly fluctuating nature of oscillations in coher-ence and phase is typical of illustrations presented in phys-iology reports [8, pp. 68–82; 12, p. 29; 13, pp. 134–137, and others]. The situation with averaged coherence values is no better (see below).


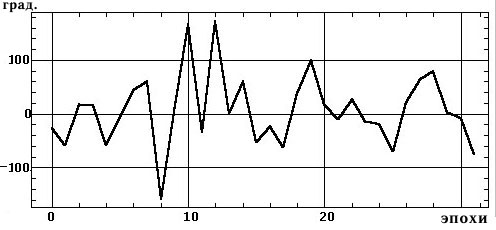
Fig. 2. Changes in cross-spectrum phase (Fig. 1, c) for the dominant alpha-rhythm frequency of 9 Hz (Fig. 1, b) at 32 sequential 2-sec epochs

     Sharp reductions in the accuracy of calculations for small signal amplitudes should be noted, these being characteristic of high-frequency ranges and due to the limited data element length resulting from the integer-based representation of the output of analog-to-digital converters – low-amplitude harmonics are represented by the least significant bits. This affects first the accuracy of calculations of autospectrum and cross-spectrum amplitudes and then, to a greater extent, coherence values. This effect is a further source of error in coherence analysis.1 In this regard we must not criticize modern ACD with high bit coding (up to 24-bit) which use delta-sigma conversion; these ACD record all signals from the surrounding space and particularly the high-amplitude network noise. After its removal by digital filtration, the extracted EEG signal is generally located in the 8–12 least significant bits.
     Thus, coherence is extremely dependent on random fluctuations resulting from fundamental instrument errors associated with DFT and the properties of the EEG processes themselves. This also has the result that coherence cannot be regarded as an informative measure for evaluat-ing the levels of synchronicity of EEG processes. According to the popular expression: anything can be extracted from Gaussian noise.

     Dependence on noise level. An important question, ignored in the literature, is that of elucidating the relation-ship between coherence and the levels of noise in the sig-nals being analyzed. We will address this using a statistical modeling method, which is based on a very simple concept. The instantaneous spectra X(f) and Y(f) of monoharmonic processes x(t) and y(t) are generated by geometrical summation of two components: a) a defined vector of length r with a range of values r = 0-1 with a fixed phase angle (for example, 0°), and b) a random vector of length 1 r with a phase angle selected randomly in the range 0–360°. Each coherence value is calculated by averaging 30 pairs of such instantaneous spectra and the mean value is calculated using 1000 g2 values calculated in this way.an essentially linear relationship with noise, i.e., 20–60%; 4) when signals contain more than 30–40% noise it becomes difficult to claim a high level of synchronicity between EEG processes, such that only g2 values of >0.7 are acceptable for this.
ntent in the narrow range over which the curve shows an essentially linear relationship with noise, i.e., 20–60%; 4) when signals contain more than 30–40% noise it becomes difficult to claim a high level of synchronicity between EEG processes, such that only g2>0.7 are acceptable for this.
     The relationship between the mean value of g2 and the noise content in the signal (0–r)% is shown in Fig. 3, and this plot leads to the following conclusions: 1) The Sshaped nature of this relationship fundamentally distinguishes coherence from the correlation coefficient, whose relationship with the noise level is essentially linear; 2) at noise levels exceeding 60%, the relationship is largely flattened, so over this range g2 cannot serve as a measure of the noise content or the extent of desynchronization of EEG processes; 3) g2 can only be a satisfactory indicator of noise content in the narrow range over which the curve shows


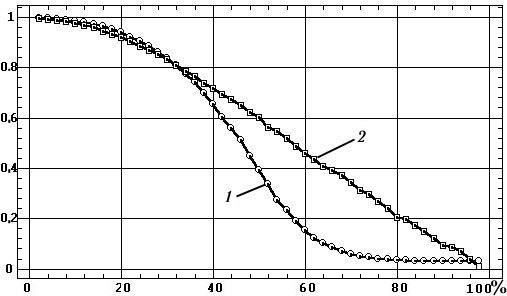
Fig. 3. Relationship between coherence values (1) and correlation coefficients (2) and the proportion of noise in the signal.

     These conclusions are supplemented by data reported in [1, p. 308] on the number of averagings n required to obtain significant values of g2 with errors levels of less than ±0.1 depending on the true value of g2 (Table 2). As the non-stationarity of EEG processes over prolonged periods of time has the result that the number of averagings available for coherence calculations is generally no more than 10, it follows that only values of g2>0.8 can be regarded as satisfactorily significant.
     However, scientific reports generally discuss experimental assessments of coherence in the range 0.1–0.8 and use these to draw physiological conclusions. These conclusions may therefore be extremely mediocre evaluations of the levels of synchronicity of EEG processes.
 

TABLE 2. True g2 Coherence Values and Numbers of Ensembles Needing to be Analyzed n to Obtain True g2 Values with Errors not Exceeding ±0.1

     Computer analyzers. What situation applies to the various commercialized programs for coherence calcula-tions? We asked several leading and senior EEG analyzer producers (in Moscow, St. Petersburg, Taganrog, Ivanovo, Kharkov) about their algorithms for calculation of coherence and received responses whose agreement was far less than 100%.
     Testing of a number of program bundles using identical EEG traces showed (uniformity of testing was hindered by the incompatibility of the programs in terms of loading traces in the international EDF format) that the correspondence of coherence spectra applies only in relation to their integral characteristics (one comparison example is shown in Fig. 4): plots were monotonic or multipeak, had neighboring high or low values at particular frequencies, and had approximate coincidence of the frequency values of certain peaks. Other qualitative characteristics, as well as quantitative evaluations, showed significant differences. This would appear to result from the relationship between coherence values and a multitude of parameters undeclared on the packaging and uncontrolled: squared or nonsquared versions of the computations, the length of the analysis epoch, the number of epochs averaged, the magnitude of the time shift between epochs, the use of a correcting window, the type of final smoothing of the coherence function, etc.


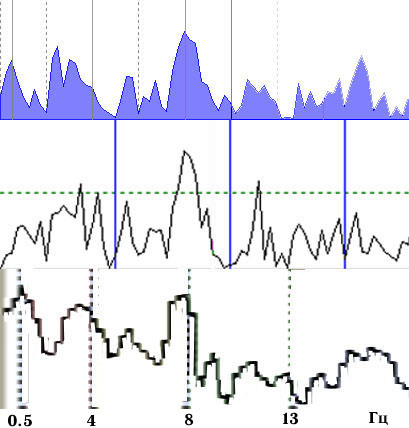
Fig. 4. Coherence spectra calculated using three EEG analyzers, epoch length 4 sec, average of 16 epochs..

     An example of the dependence of a coherence spectrum on the duration of the epochs being averaged and the correcting window is shown in Fig. 5. This clearly shows that the results are significantly different in terms of the positions, shapes, and amplitudes of the dominant peaks.


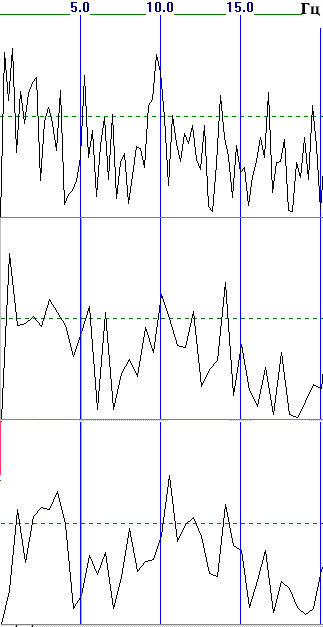
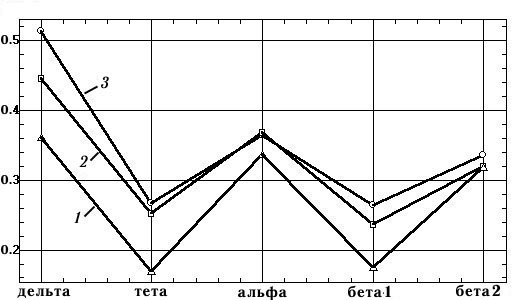
Fig. 5. Relationship between coherence and analysis epoch duration T and use of a correcting window (average of 16 epochs); above downwards: T = 4 sec; T = 2 sec; T = 2 sec + Hann correcting window..

     Figure 6 shows plots of the mean coherence values in standard frequency ranges calculated for the spectra of Fig. 5. The range of variation of coherence values is very large – amounting to 28–36% of the maximum value (in the delta, theta, and beta1 ranges). Thus, the mean coherence calculated using different values for the parameters are not comparable in quantitative terms. The variability increases even more when we calculate mean coherence for a group of subjects [8, pp. 71, 74], when most paired differences in coherence, on the background of large standard deviations, are statistically insignificant.


Fig. 6. Variability of mean coherence values in frequency ranges in relation to analysis epoch duration and use of a correcting window (average of 16 epochs): 1) T = 4 sec; 2) T = 2 sec; 3) T = 2 sec + Hann correcting window

     It should also be noted that recent years have seen the increasing introduction of new spectral analysis methods based on wavelets, which produce results even more fundamentally (both quantitatively and qualitatively) different from the results obtained using traditional DFT and, thus, from the whole assemblage of data accumulated over many decades.
     Thus, coherence analysis results obtained using dif-ferent program bundles and with different values for the parameters are poorly comparable in qualitative and quantitative terms, as are any scientific conclusions based on these results.

     Conclusions. This multilateral analysis of the fundamental disadvantages of coherence functions (identification of the influences of a multitude of uncontrolled fandom factors, inapplicability to EEG analysis, dependence on a number of adjusting factors, the nonlinearity of the dependence on the noise level, dependence on phase and amplitude variability, the non-comparability of the results obtained, etc.) indicates that this numerical characteristic cannot, on the basis of metrological considerations, be supported as an analytical tool in the current understanding of this term.
     Alternatives. Many investigators have in recent years recognized the stationary-segments paradigm of EEG structure [3], such that various approaches can be applied to EEG traces using relatively stationary segments with a criterion for the synchronicity of the time dynamics of such structures. One potential approach in this direction [4 and others] is based on segmentation for areas of increased/decreased amplitude modulation of signals, with evaluation of the synchronicity of two leads in terms of the proportion of coinciding intersegment transitions (an algorithmic approach to this method is presented in [6, pp. 227–230, 251–254]. Another approach consists of using Pearson correlation coefficients to assess the synchronicity of EEG modulation rhythms in a selected time period. Both of these methods have now been verified and the results obtained using them demonstrate their applicability to many probems and their potential.

REFERENCES

1. J. Bendat and A. Pirsol, Measurement and Analysis of Random Processes [Russian translation], Mir, Moscow (1971).
2. G. Jenkins and D. Watts, Spectral Analysis and its Applications [Russian translation], Mir, Moscow (1971).
3. A. Ya. Kaplan, “EEG nonstationarity: methodological and experimental analysis,” Usp. Fiziol. Nauk., 29, No. 3, 35–55 (1998).
4. A. Ya. Kaplan, S. V. Borisov, S. L. Shishkin, and V. A. Ermolaev, “Analysis of the segment structure of human EEG alpha activity,” Ros. Fiziol. Zh., 4, 84–95 (2002).
5. A. P. Kulaichev, “Some methodological problems of EEG frequency analysis,” Zh. Vyssh. Nerv. Deyat., 47, No. 5, 918–926 (1997).
6. A. P. Kulaichev, Computerized Electrophysiological and Functional Diagnosis [in Russian], FORUM-INFRA-M, Moscow (2007).
7. M. N. Livanov, Temporospatial Organization of Potentials and Systems Activity in the Brain [in Russian], Nauka, Moscow (1989).
8. M. N. Livanov, V. S. Rusinov, P. V. Simonov, M. V. Frolov, O. M. Grin-del, G. N. Boldyreva, E. M. Vakar, V. G. Volkov, T. A. Maiorchik, and N. E. Sviderskaya, Diagnosis and Prognosis of the Functional State of the Brain [in Russian], Nauka, Moscow (1988).
9. S. L. Marple, Jr., Digital Spectral Analysis and its Applications [Russian translation], Mir, Moscow (1990).
10. R. Otnes and L. Enoxon, Applied Analysis of Time Series [Russian translation], Nauka, Moscow (1978).
11. R. B. Randall, Frequency Analysis, Bruel and Kjaer, Copenhagen (1989).
12. V. S. Rusinov, O. M. Grindel, G. N. Boldyreva, and E. M. Vakar, Biopotentials in the Human Brain [in Russian], Meditsina, Moscow (1987).
13. V. D. Trushch and A. V. Korinevskii, Computers in Neurophysio-logical Studies [in Russian], Nauka, Moscow (1978).
14. W. R. Adey and D. O. Walter, “Application of phase detection and averaging techniques in computer analysis of EEG records in the cat,” Exper. Neurol., 7, 186–209 (1963).
15. N. R. Goodman, “Measuring amplitude and phase,” J. Franklin Inst., 270, 437–450 (1960).
16. G. Nolte, O. Bai, L. Wheaton, Z. Mari, S. Vorbach, and M. Hallett, “Identifying true brain interaction from EEG data using the imagi-nary part of coherency,” Clin. Neurophysiol., 115, 2292–2307 (2004).
17. D. O. Walter, “Spectral analysis for electroencephalograms: Mathe-matical determination of neurophysiological relationships from records of limited duration,” Exper. Neurol., 8, 155–181 (1963).