Об информативности когерентного анализа в исследованиях ЭЭГ
г Кулаичев А.П.
ссылки при цитировании: Журнал высшей нервной деятельности. 2009. 59(6): 766-775
Инициацию внедрения математических методов в электроэнцефалографию традиционно
связывают с именем Н. Винера, который в 1936 г. высказался за применение
корреляционного анализа, рассматривая ЭЭГ как стационарный волновой процесс.
Именно интенсивным внедрением математических методов характеризовался первый
этап развития компьютерной электрофизиологии [6, с. 20—32]. Это внедрение
происходило с высоким энтузиазмом физиологов и сотрудничавших с ними инженеров.
Однако профессиональные математики, не видя для себя высокой научной престижности
глубокого погружения в данную область, ограничивались, как правило, общими
теоретическими предложениями, выражаемыми в интегральной форме. Инициативное
же внедрение математических методов техническими специалистами привело
к распространению в физиологической среде целого ряда некорректных и даже
ошибочных методов, понятий и представлений. В первую очередь не учитывались
два основных отличия ЭЭГ–сигналов от большинства сигналов физического происхождения:
а) принципиальная нестационарность; б) амплитудная модулированность во
всех частотных диапазонах. В особо критической степени сказанное относится
к когерентному анализу, на что ранее частично уже обращалось внимание [5].
Источники.
Согласно [7, с. 138]: «Гудманом в 1960 г. [15] была предложена, а в работе
[14] впервые применена к анализу биоэлектрической активности мозга так
называемая функция когерентности». С одной стороны, в работе [15] когерентность
никоим образом не рассматривается и не упоминается, а развитие методов
спектрального анализа происходило задолго до этого и было резюмировано
в фундаментальных монографиях таких известных авторов, как Барлетт М.С.,
1955; Бендат Дж. С., 1958; Блекман Р.Б. и Тьюки Дж.В., 1959 и др.
С другой стороны, формула когерентности применительно к электрофизиологии
была приведена и прокомментирована (без ссылок на источники) одним из авторов
работы [14] в более позднем исследовании [17]. К тому же сегодня почти
никто не вспоминает, что изначально функция когерентности была разработана
в 1930 г. Д. Гильбертом и Н. Винером применительно к задачам оптики и квантовой
механики.
Далее необходимо отметить, что в многочисленной специальной литературе
в отношении когерентности имеется ряд недосказанностей. Так, функция когерентности
процессов x(t) и y(t) (иногда она называется
квадратом когерентности) обычно задается формулой:
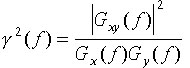 ,
(1)
,
(1)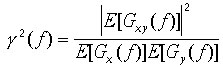 ,
(9)
,
(9) Потребности
электрофизиологии. В физиологии ВНД важно
иметь надежные оценки различных аспектов синхронизма ЭЭГ–процессов. В случае
высокого синхронизма можно затем предполагать и верифицировать наличие
различных форм физиологической связи процессов: влияние одного процесса
на другой, влияние на них общего источника, искать топографические паттерны
высокосинхронных связей с целью дифференциации функциональных состояний,
личностных особенностей, нормы и патологии, влияния медикаментозных препаратов
и т.п.
Привлечение когерентности для таких целей, по–видимому, в значительной
степени было определено повторяющимся в литературе и недостаточно аргументированным
утверждением о том, что когерентность в частотной области является аналогом
коэффициента корреляции Пирсона во временной области [2, с. 112; 10, с.
342; 11, с. 270; 13; с. 36; 17, с. 172]. Как дважды будет показано далее,
подобные утверждения существенно далеки от действительности. Здесь же,
в частности, отметим, что: а) когерентность (1) можно соотнести
только с квадратом коэффициента корреляции, который в практике крайне редко
используется; б) в отличие от когерентности диапазон значений коэффициента
корреляции составляет от –1 до +1.
Интерпретация
когерентности. Формула (9) не позволяет
дать прямую и наглядную содержательную интерпретацию когерентности. Поэтому
рассмотрим другое допустимое уточнение формулы (1) [6, с. 196], знаменатель
которого преобразуем по соотношению (7):
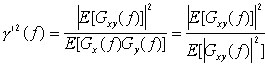 , (10)
, (10)Таблица 1. Зависимость когерентности от амплитудно-фазовых соотношений спектров двух моногармонических сигналовТем самым когерентность g2 дает завышенные оценки в отношении степени синхронизма процессов, причем со сложной зависимостью от степени их амплитудной вариабельности. Этим когерентность принципиально отличается от коэффициента корреляции как устойчивого индикатора линейной связи двух парных переменных, не зависящего от соотношения диапазонов их значений.
Погрешности
спектрального анализа. Одной из главных
погрешностей дискретного преобразования Фурье (ДПФ) считается эффект утечки
или вытекания мощности из спектральных пиков на соседние спектральные линии.
Для его уменьшения в технических приложениях используются различные корректирующие
окна, и эта методика была некритически перенесена и в электрофизиологию.
Однако, в работе [6, с. 200] показано, что окна оказывают на спектральные
пики двоякий эффект: они стягивают размытые пики, но размывают хорошо локализованные
пики. Поэтому в исследованиях ЭЭГ более корректным для вычисления средних
и максимальных амплитуд спектра является использование предварительной
фильтрации сигнала в анализируемом диапазоне, исключающей утечку и модуляционные
пики из соседних диапазонов.
Однако эффект утечки зависит от соотношения периода гармоники и эпохи анализа
[6, с. 200]: при целом числе периодов гармоники на эпохи анализа утечка
отсутствует, при полуцелом числе периодов гармоники на эпохи анализа утечка
максимальна. Кроме того, даже в последнем случае утечка уменьшается обратно
пропорционально удалению от основного пика. Вместе с тем существует и еще
одно, не замеченное ранее и существенное искажение спектра, связанное с
амплитудной модуляцией, присущей всем ЭЭГ–сигналам. Этот эффект [6,
с. 187] проявляется в появлении двух симметричных боковых пиков, достигающих
40% и более от амплитуды центрального пика и отстоящих от него на число
спектральных линий, равных числу наблюдаемых периодов модуляции сигнала
(это имеет место для моногармонического сигнала, а картина для реальной
ЭЭГ будет значительно сложнее).
Эти две основные погрешности вызывают в спектрах
дополнительные (к отмеченным выше) случайные флюктуации, особо визуально
выраженные при высоком частотном разрешении. Таким флюктуациям в большей
степени подвержены фазовые спектры в отличие от амплитудных спектров.
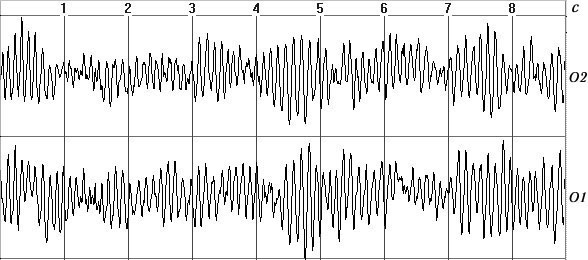 а)
а)
 б)
б)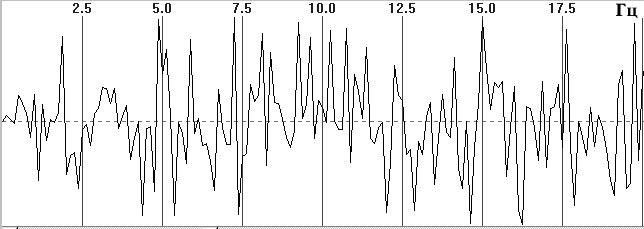 в)
в)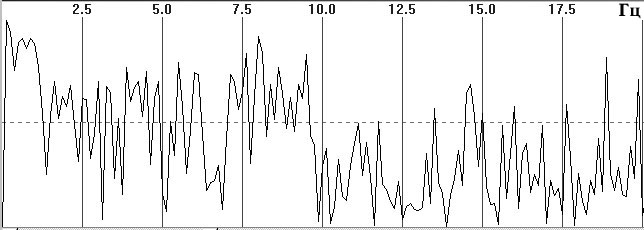 г)
г)
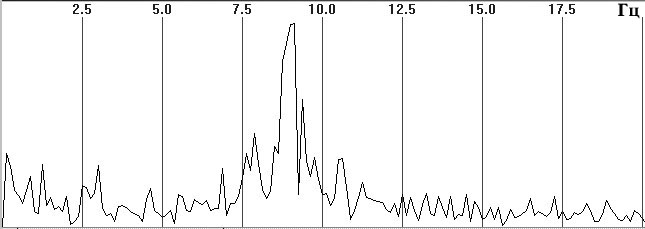
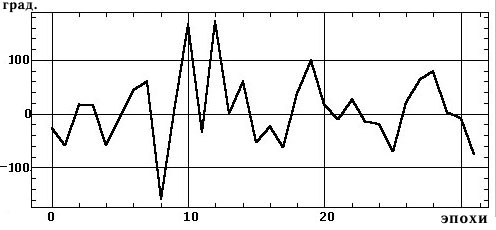
На рис. 1, а приведен небольшой фрагмент типичной и продолжительной ЭЭГ–записи с высоким содержанием альфа–ритма в затылочных отведениях. На рис. 1, б приведен амплитудный кросс–спектр между этими двумя процессами на эпохе анализа 8 с, где выделяется высокоамплитудный пик на основной частоте альфа–ритма 9 Гц. Заметно также присутствие низкоамплитудных случайных флюктуаций во всем частотном диапазоне. На рис. 1, в, г приведены фазовый кросс–спектр и спектр когерентности, в которых уже полностью преобладают случайные флюктуации и не прослеживается отчетливой частотной закономерности. На рис. 2 приведен график изменения фазы кросс–спектра на основной частоте альфа–ритма 9 Гц для 32 последовательных эпох. Видно, что фаза (стабильность которой в значительной степени отражает когерентность) по эпохам случайно и резко колеблется в широком диапазоне +-160 град. Подобный случайно–флюктуационный характер колебаний когерентности и фазы типичен для иллюстраций, приводимых в физиологических публикациях [8, c. 68—82; 12, с. 29; 13, с. 134—137 и др.]. Ничуть не лучше обстоит дело с усредненными значениями когерентности (см. далее).
Следует также отметить резкое снижение точности вычислений для малых амплитуд
сигнала, характерных для высокочастотных диапазонов, в связи с ограничением
разрядной сетки целочисленного представления результатов аналого–цифрового
преобразования — малые по амплитуде гармоники представлены в самых младших
разрядах сетки. Это сказывается сначала на точности вычислений амплитуд
автоспектров и кросс–спектров, а затем, и в большей степени, — на значениях
когерентности. Этот эффект является еще одной из погрешностей когерентного
анализа (в этом плане нас не должны смущать высокоразрядные
(до 24 двоичных разрядов) современные АЦП, использующие принцип дельта–сигма
преобразования; такие АЦП регистрируют все сигналы окружающего пространства
и главным образом — высокоамплитудную сетевую наводку, после ее удаления
посредством цифровой фильтрации выделенный ЭЭГ–сигнал локализуется,
как правило, в 8—12 младших разрядах).
Тем самым когерентность демонстрирует крайне высокую степень зависимости
от случайных флюктуаций, вызванных основными инструментальными погрешностями
ДПФ и свойствами самих ЭЭГ–процессов. Это также не позволяет рассматривать
когерентность в качестве информативного показателя для оценки степени синхронизма
ЭЭГ–процессов.
Риторический вопрос: как можно пользоваться
инструментом, подверженным стольким случайным погрешностям?
Зависимость от уровня шума. Важным и не рассмотренным в литературе вопросом является выяснение зависимости когерентности от уровня шума в анализируемых сигналах. Используем для этого метод статистического моделирования, идея которого предельно проста. Мгновенные спектры X(f), Y(f) моногармонических процессов x(t) и y(t) генерируются в результате геометрической суммы двух составляющих: а) детерминированного вектора длины r в диапазоне значений r = 0–1 с фиксированным фазовым углом (например, 0 град.); б) случайного вектора длины 1–r с фазовым углом, случайно выбираемым в диапазоне 0–360 град. Каждое значение когерентности вычисляется усреднением по 30 парам таких мгновенных спектров, среднее значение вычисляется по 1000 таким образом полученным g2.
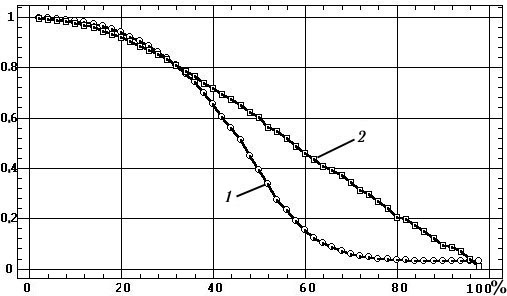
Зависимость среднего значения g2
от содержания шума в сигналах (0–r)% приведена на рис. 3, и этот график
позволяет сделать следующие очевидные выводы: 1)
S–образный характер зависимости принципиально отличает когерентность от
коэффициента корреляции, зависимость которого от уровня шума имеет преимущественно
линейный характер; 2)
при уровне шума более 60% зависимость практически выполаживается, поэтому
в этом диапазоне g2
не может служить индикатором содержания шума или степени десинхронизма
ЭЭГ–процессов; 3)
удовлетворительным индикатором содержания шума g2
может быть только в узком диапазоне приблизительно линейной зависимости
от шума: 20–60%; 4)
при наличии в сигналах шума более 30–40% становится проблематичным обоснованное
утверждение о высоком синхронизме ЭЭГ–процессов, тем самым приемлемыми
в этом плане могут быть лишь значения g2>0.7.
Эти выводы дополняются данными работы [1, с. 308] о необходимом числе усреднений
n для получения достоверных значений g2
с ошибкой менее +-0.1 в зависимости от истинного значения g2
(табл. 2). Поскольку в связи с нестационарностью ЭЭГ–процессов на продолжительных
временных интервалах число усреднений для вычисления когерентности обычно
не превосходит 10, то отсюда следует, что удовлетворительно достоверными
могут считаться лишь значения g2>0.8.
Однако в научных публикациях обсуждаются экспериментально полученные оценки
когерентности, обычно находящиеся в диапазоне 0.1–0.8, и именно по ним
делаются физиологические выводы. Поэтому такие выводы имеют крайне посредственное
отношение к оценке степени синхронизма ЭЭГ–процессов.
Риторический вопрос: как можно пользоваться
эталоном длины, размер которого нелинейно меняется в зависимости от измеряемого
расстояния?
Компьютерные
анализаторы. Как же обстоит дело с вычислением
когерентности в представленных на рынке многочисленных и разнородных программных
пакетах? Мы конфиденциально опросили ряд ведущих и старейших производителей
ЭЭГ–анализаторов (Москва, Санкт–Петербург, Таганрог, Иваново, Харьков)
об используемых ими алгоритмах вычисления когерентности и получили далеко
не 100%–но совпадающие ответы.
Проведенное тестирование нескольких пакетов на одинаковых ЭЭГ–записях показало
(унификация тестирования осложняется несовместимостью пакетов по обмену
записями в международном EDF–формате), что о соответствии спектров когерентности
можно говорить лишь в плане их интегральных характеристик (один из примеров
сравнения приведен на рис. 4): монотонный или многопиковый характер, сосредоточение
высоких или низких значений в определенных частотных диапазонах, приблизительное
совпадение частотной локализации отдельных пиков. Другие же качественные
характеристики, а также количественные оценки существенно различаются.
Это, видимо, определено зависимостью значений когерентности от множества
недекларированных и нерегулируемых в пакетах параметров: от квадратичного
или неквадратичного варианта вычислений, от длины эпохи анализа, от числа
усредняемых эпох, от величины временного сдвига между эпохами, от применяемого
корректирующего окна, от характера завершающего сглаживания функции когерентности
и др.
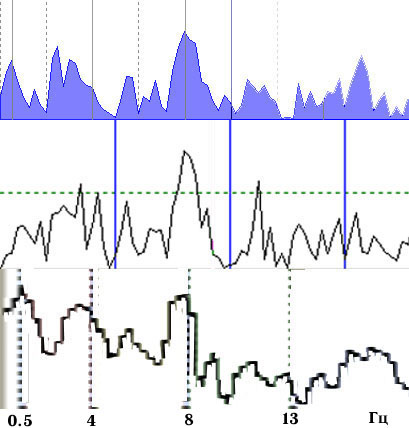
Риторический вопрос: как можно пользоваться инструментом, для которого не существует эталонов, а различные его реализации дают различные и несопоставимые результаты?
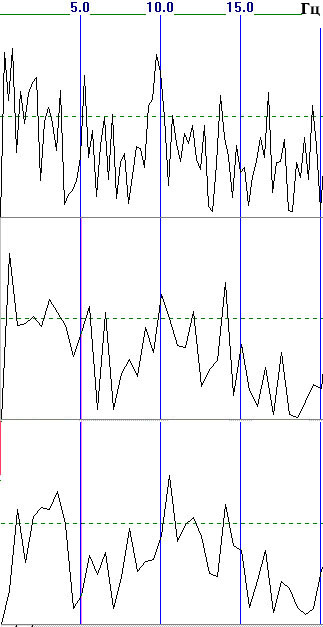
Пример зависимости спектра когерентности от длины усредняемых эпох и корректирующего окна приведен на рис. 5. Как нетрудно заметить, результаты существенно различаются по расположению, форме и амплитуде доминирующих пиков.
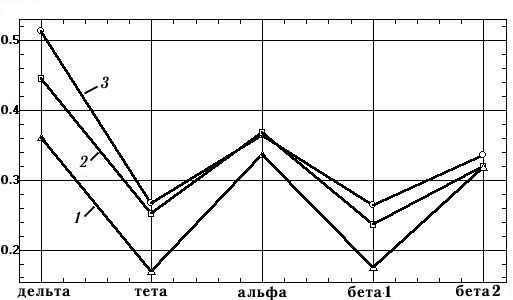
На рис. 6 приведены графики средних значений когерентности в стандартных частотных диапазонах, вычисленные для спектров рис. 5. Видно, что вариационный размах значений когерентности очень велик — его отношение к максимальным значениям доходит до 28—36% (в дельта–, тета– и бета1–диапазонах). Тем самым средние значения когерентности, вычисленные при различных значениях установочных параметров, количественно несопоставимы. Эффект вариабельности еще более усиливается при вычислении средних значений когерентности по группе испытуемых [8, с. 71, 74], когда большинство парных различий когерентности на фоне больших стандартных отклонений являются статистически недостоверными.
Риторический вопрос: как можно пользоваться инструментом, результаты измерения которым зависят от положения многих регулировочных ручек?
Следует также отметить, что в последние годы в практику стали внедряться
и новые методы спектрального анализа на основе вайвлетов, результаты которого
еще более кардинально (как количественно, так и качественно) отличаются
от результатов, полученных с использованием традиционного ДПФ, а следовательно,
и от всего их накопленного за многие десятилетия многообразия.
Таким образом, результаты когерентного анализа, полученные в различных
программных пакетах и при различных значениях установочных параметров,
равно как и производимые на их основе научные выводы плохо сопоставимы
как качественно, так и количественно.
Выводы.Из
произведенного многостороннего анализа принципиальных недостатков функции
когерентности: подверженность влиянию множества неконтролируемых случайных
факторов, неадекватность задачам исследования ЭЭГ, зависимость от ряда
регулировочных параметров, нелинейность зависимости от уровня шума, зависимость
от фазовой и амплитудной вариабельности, несопоставимость получаемых результатов
и др. следует, что эта числовая характеристика с метрологических позиций
никоим образом не может быть квалифицирована в качестве измерительного
инструмента в современном понимании этого термина.
Альтернативы.
В последние годы внимание многих исследователей привлекает парадигма кусочно–стационарной
структуры ЭЭГ [3], исходя из которой запись ЭЭГ с использованием различных
подходов структурируется на сегменты относительной стационарности и ищутся
критерии синхронности временной динамики таких сегментных структур. Один
из перспективных подходов в этом направлении [4 и др.] базируется на сегментации
по участкам увеличения–уменьшения амплитудной модуляции сигналов с оценкой
синхронности двух отведений по проценту совпадающих межсегментных переходов
(алгоритмическая реализация метода изложена в работе [6, с. 227–230, 251–254]).
Другой подход состоит в использовании коэффициента корреляции Пирсона для
оценки синхронности модуляционной ритмики ЭЭГ на выбранном временном интервале.
В настоящее время оба метода всесторонне апробируются, и предварительные
результаты свидетельствуют о их многоплановой эффективности и перспективности.
СПИСОК ЛИТЕРАТУРЫ