Введение. Факторный анализ является наиболее значимым и часто используемым из многомерных методов, а методы кластеризации и дискриминантного анализа дают более наглядные результаты, если они применяются к данным, уже прошедшим процедуру факторизации. Однако, в большинстве учебников этот раздел излагается непредметно, несистематично, ненаглядно или же чрезмерно формально [1, 4—6, 10, 12—15]. Ниже мы излагаем дидактику, доказавшую свою действенность в нашей многолетней преподавательской практике и более детально проиллюстрированную в [7].
    Во введении в факторной анализ надо обратить внимание аудитории на следующие принципиальные моменты:

• опосредованность и относительность исходных переменных, не отражающих истинные действующие факторы;
• эти скрытые факторы могут проявляться в нескольких переменных (коррелированность);
• сила влияния фактора проявляется в диапазоне изменения переменных (дисперсия);
• первая задача анализа — найти главные действующие факторы;
• простой и понятный предметный иллюстрирующий пример.

    Учебный пример. Все вышесказанное следует проиллюстрировать на наглядном геометрическом примере. Пусть имеется трехмерное пространство исходных переменных х1, х2, x3. Наполним это пространство 100 нормально распределенными объектами так, чтобы эти объекты группировались вдоль диагонали куба, построенного на осях координат этого пространства, а разброс положения объектов в направлении диагонали был бы в 2 и 4 раза больше по сравнению с разбросом по двум другим, перпендикулярным к диагонали и друг к другу направлениям. Такому распределению отвечает огромное разнообразие реальных данных с высокими корреляциями между переменными, например: измерения роста, веса и жизненной емкости легких (ЖЕЛ) у множества людей — ясно, что в данном случае все эти переменные определяются общим главным фактором, который можно условно назвать фактором "антропометрического масштаба". Можно придать предметный смысл и двум другим факторам следующим образом. Пусть мы производим эти антропометрические измерения у двух профессиональных категорий: штангистов и марафонцев. Очевидно, что вторым фактором будет фактор профессии, определяющий значительный систематический сдвиг значений (дисперсию) в плоскости вес—рост. С другой стороны, третий фактор пола будет определять сдвиг (дисперсию) в перпендикулярном направлении, поскольку при тех же соотношениях роста и веса женщины в среднем будут иметь меньшую ЖЕЛ, чем мужчины.
 

а)

б)

Назначение метода.Первой практически значимой задачей факторного анализа является нахождение системы существенных или действенных факторов в пространстве регистрируемых переменных (а вовсе не отвлеченное от предметности некое "снижение размерности"). В процессе решения и развития этой задачи могут присутствовать несколько последовательных этапов:

• вычисление главных факторных компонент как новой координатной системы, расположенной по осям эллипсоида рассеяния анализируемых данных;
• волевой (содержательный) выбор в качестве факторов тех из главных компонент, которые отвечают за большую часть дисперсии (рассеяния) анализируемых данных;
• коррекция выделенных факторов специальными методами факторного анализа с целью достижения большей адекватности факторной модели исходным данным по ряду критериев;
• вращение выделенных факторов с целью обеспечения их лучшей проецируемости на исходные переменные для облегчения последующей предметной интерпретации;
• содержательная интерпретация факторов в предметных (физических) терминах, что является творческой задачей, выходящей за рамки формального метода, однако она может принести много полезного для дальнейшего понимания объекта исследования;
• исследование распределений объектов в их проекциях на плоскости главных факторов (в новых факторных координатах объектов).

Исходные данные чаще всего представляются в виде матрицы значений m переменных для n объектов или измерений. При подготовке исходных данных важны следующие рекомендации:
    1. Из статистических соображений желательно, чтобы число объектов или измерений было бы не меньше числа переменных, еще предпочтительнее, чтобы их было в 2—3 раза больше. Невыполнение этого условия может привести к неадекватному завышению числа главных факторов, к искажениям факторных нагрузок исходных переменных и распределения объектов в факторном подпространстве.
    В исследованиях опросного характера к объему данных предъявляются более жесткие требования: выборка, размер которой 50 респондентов, оценивается как очень плохая, 100 — плохая, 200 — средняя, 300 — хорошая, 500 — очень хорошая, 1000 — превосходная.
    При малом числе объектов мы рекомендуем проводить факторный анализ повторно с удалением из анализа тех исходных переменных, которые близки между собой по векторам факторных нагрузок, оставляя по одной переменной из каждой такой группы.
    2. Желательно предварительно удалить из данных сильные выбросы (более трех стандартных отклонений), поскольку они могут существенно повлиять на перераспределение дисперсии между переменными.
    3. Желательно также найти все пары переменных, связанные между собой четкими функциональными зависимостями, и оставить по одному представителю из каждой такой пары. В противном случае такие зависимые переменные будут существенно смещать дисперсию объектов, а следовательно — и вектора факторов.
    Корреляции. Исходным материалом для процедуры факторного анализа является корреляционная матрица mm, вычисленная между всеми парами переменных в исходной матрице mn. Корреляции могут вычисляться различными методами, наиболее часто в практике используются:
    1) параметрические коэффициенты корреляции Пирсона применяются в случае метрических и нормально распределенных исходных данных;
    2) ковариации представляют собой взаимные вариации между переменными, их использование сравнительно менее употребительно, но позволяет в вычислениях учитывать не только степень взаимосвязанности (коррелированности) переменных, но и абсолютную величину ковариаций;
    3) непараметрические коэффициенты корреляции Спирмана и конкордации Кенделла применимы в случае ненормально распределенных числовых данных и ранговых переменных;
    4) коэффициенты связности Крамера применимы для номинальных и ранговых переменных;
    5) коэффициенты связности бинарных признаков, вычисляются для таблиц кросстабуляции размера 2x2 по различным формулам: (a+d)/(a+b+c+d); a/(a+b+c+d); 2a/(2a+b+c); a/(a+2(b+c)); (ad-bc)/ (a+b+c+d)^2 и др., где a, b, c, d — частоты встречаемости пар значений признаков

    Главные компоненты. Изложение результатов факторного анализа следует начинать с метода главных компонент, как наиболее интуитивно познаваемого и допускающего наглядные геометрические иллюстрации (рис. 1).
    Необходимо напомнить, что главные компоненты вычисляются по корреляционной матрице и представляют собой новую координатную систему, повернутую по главным осям эллипсоида рассеяния объектов. Для последующего использования исходные данные стандартизуются по каждой переменной (вычитанием среднего значения и делением на стандартное отклонение), чтобы нивелировать различия в единицах измерения и масштабах.
    Выделение главных компонент отвечает наиболее распространенной, так называемой канонической модели факторного анализа, в которой исходные переменные линейно выражаются через факторы, а факторы не коррелированы между собой и со случайными (специфическими) остатками модели, а случайные остатки в свою очередь взаимно не коррелированы и нормально распределены. Вычисление главных компонент также обычно используется как первый этап в других методах факторного анализа (см. ниже) для выявления значимых или общих факторов.
    Оценка сравнительной значимости главных компонент производится по их собственным значениям li, представляющим собой дисперсию стандартизированных исходных данных по данной компоненте — "объясняемую" ей часть общей (суммарной по переменным) дисперсии объектов. Эти значения обычно сопровождаются соответствующими им процентами полной дисперсии и процентами накопленной дисперсии. Для рассматриваемого примера таблица собственных значений имеет вид:

Рис. 2. Пример графика собственных значений главных компонент

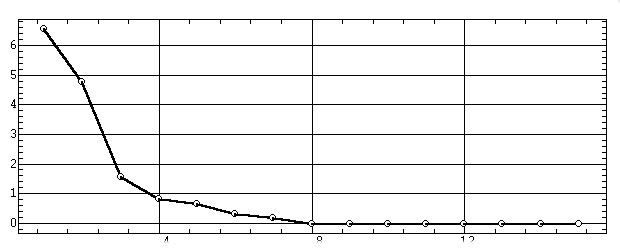
    Выбор числа значимых факторов. Полученные результаты позволяют произвести выбор числа значимых или, как их обычно называют, общих факторов для последующего анализа или вращения.

Для этого можно использовать три критерия:

• критерий Кайзера состоит в отбрасывании компонент, собственные значения которых меньше единицы, что далеко не всегда оправдано [Мотивируется это следующим образом: поскольку дисперсия нормализо-ванных переменных равна единице, то компоненты с меньшими собственными значениями (а они отражают факторную дисперсию) менее значимы, нежели сами переменные. Однако часто встречается ситуация (например, при малом числе переменных или при высокой корреляции только между двумя из них), когда уже второй компонент имеет собственное значение, меньшее единицы, а тогда по рассматриваемому критерию факторный анализ становится бессмысленным];
• критерий Кеттелла использует на графике собственных значений точку перегиба к его выполаживанию (на рис. 2 это соответствует 3—4 факторам);
• отбрасывание компонент, суммарно отражающих менее 5—30% общей дисперсии.

    Собственные вектора. Во многих учебниках после рассмотрения собственных значений сразу производится скачек к сравнительно сложным для восприятия факторным нагрузкам [3, 8, 9]. Однако дидактически правильным является первоначальное рассмотрение собственных векторов (вектора главных компонент), которые допускают прямое геометрическое представление, вычисляются во всех пакетах матричной алгебры, однако в ряде учебников вообще не упоминаются.
    Матрица собственных векторов |Aij| содержит коэффициенты перехода aij от координатной системы исходных переменных X (строки) к координатной системе главных компонент X' (столбцы):

x'=x*Cos(a)+ySin(a);
y'=-x*Sin(a)+yCos(a);
Cos²(a)+Sin²(a)=1.

Рис. 3. Соотношения исходной X, Y и факторной X’, Y’ систем координат. Показаны проекции точки А на исходную и факторную систему координат.

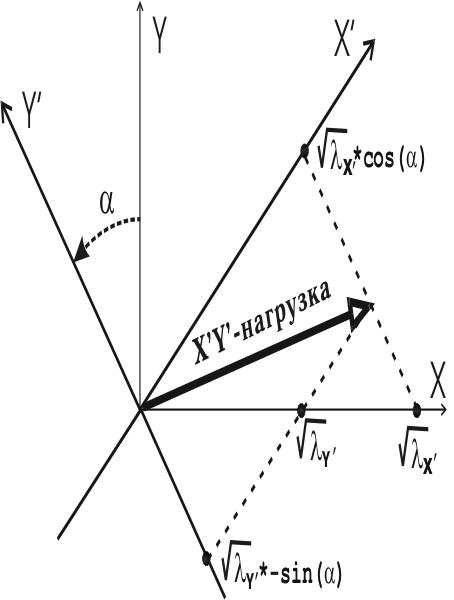
    Факторные нагрузки. Математически факторная нагрузка равна векторному коэффициенту aij перехода от переменной j к фактору i, умноженному на корень квадратный из собственного значения фактора:
  . Тем самым, факторная нагрузка показывает насколько геометрически близка переменная к фактору и насколько велика с учетом этой близости выражаемая фактором часть общей дисперсии объектов.
    Просуммировав возведенные в квадрат левую и правую части этой формулы по переменным j получим, что сумма квадратов нагрузок для конкретного фактора равна собственному значению фактора (с учетом того, что по теореме Пифагора сумма квадратов коэффициентов поворота факторных осей, т.е. катетов, равна единице):
    С другой стороны, факторная нагрузка lij равна коэффициенту корреляции rij между фактором i и исходной переменной j. Это действительно так, хотя вышеприведенная формула факторной нагрузки нисколько не напоминает отношение ковариации к вариациям. Поэтому для правильного понимания обязательно следует добавить, что речь идет о корреляции между координатами объектов в проекции на фактор i и в проекции на исходную переменную j [Иначе у слушателей может возникнуть законное недоумение, а какая может быть корреляция между двумя координатными векторами и как это соотнести с типичными графическими пояснениями коэффициента корреляции?]. В этом случае отмеченная эквивалентность становится интуитивно понятной: чем меньше угол между фактором и переменной (больше косинус, т.е. aij), тем пропорционально в большей степени совпадают проекции объектов на эти два вектора, то есть больше корреляция. С другой стороны, при фиксированном угле корреляция тем больше (проекции объектов более совпадают), чем больше дисперсия в направлении фактора по сравнению с дисперсией в перпендикулярных направлениях, то есть чем больше li.
    Сумма же произведений нагрузок двух переменных (строки j, k по всем столбцам i) равна коэффициенту корреляции между этими переменными:
    При суммировании по строкам квадратов нагрузок одной переменной (i=j) получаем 1, что соответствует коэффициенту корреляции переменной с самой собой.

Рис. 4. Построение факторной нагрузки переменной Х

а)

б)

    Повторный анализ. На этом этапе бывает полезно провести повторный факторный анализ, исключив из матрицы данных близкие (или родственные) переменные. Такие близкие переменные можно выделить тремя способами:
     1) по геометрической близости их факторных нагрузок;
     2) по высоким парным корреляциям;
     3) по наличию явных функциональных зависимостей.
В результате из каждой выделенной группы близких переменных в матрице данных оставляется по одному представителю.

Рис. 6. Факторные нагрузки после добавления дубля переменной х2

Рис. 7. Объекты в проекции на плоскость факторов 1,2

а)

б)

а)

б)

    Интерпретация факторов. Факторные нагрузки являются базисом для предметной интерпретации факторов. При этом для каждого фактора выделяют группу переменных, имеющих на данный фактор наибольшие нагрузки. Затем надо попытаться обобщить предметный смысл каждой такой выделенной группы переменных и на основе этого простыми словами сформулировать предметный смысл соответствующего фактора.
    Интерпретация факторов существенно упрощается при выполнении принципа простой структуры переменных (Thurstone, 1931): каждая переменная имеет большие нагрузки (более 0,7) на один фактор и малые (менее 0,2) по всем остальным. Часто можно приблизиться к простой структуре путем пошагового сокращения числа факторов и переменных:
    а) исключение факторов, по которым ни одна из переменных не получила максимальной нагрузки;
    б) исключение переменных, получивших сравнимые и высокие нагрузки по двум и более факторам.
    Однако такое приближение к простой структуре связано с невосполнимой потерей исходной эмпирической информации, поэтому исследователь должен решать, насколько целесообразна такая потеря в свете преследуемых им целей. Требование простой структуры существенно, например, при верификации психологического теста или теоретической факторной модели. При более часто решаемых задачах — изучение структуры взаимосвязей между исходными переменными, сокращение их числа, исследование распределения объектов в системе факторов и т. п. — предметная интерпретация факторов не столь актуальна.
    Факторы могут быть униполярными, если все переменные проецируются в одном направлении фактора (положительном или отрицательном) или биполярными, если переменные распадаются на две группы, проецирующиеся в противоположенных направлениях. Следует учитывать, что эти два противоположенных факторных направления являются математической условностью, и исследователь вправе придавать им позитивный или негативный предметный смысл, исходя из семантики проецирующихся на них переменных.

    Проекции объектов в факторных координатах. По результатам факторного анализа часто бывает необходимо получить факторные координаты объектов (неудачный синоним — факторные значения [Термин «факторные значения», являющийся дословной калькой с английского, следует признать крайне неудачным. Действительно, что по-русски значит «факторные значения»? Это - значения факторов, но никак не факторные координаты объектов!]) и построить их двухмерные (рис. 10а) или же трехмерные (рис. 10б) проекции.

а)

б)

    Дальнейшие исследования. Новые координаты объектов в системе главных факторов являются важным материалом для последующих статистических исследований, а именно:
    1) выделение основных группировок объектов средствами кластерного анализа;
    2) статистическая верификация наиболее оптимальной кластеризации объектов методом дискриминантного анализа;
    3) статистические оценки парных различий выделенных кластеров;
    4) нахождение регрессионных зависимостей для распределений объектов в пространстве главных факторов.
    Многочисленные примеры подобного развития исследований из различных областей приложения приведены в [7].
    Дальнейшее продолжение анализа может состоять также в факторном прогнозировании, во вращении факторов или в применении других методов факторного анализа.

    Факторное прогнозирование. Во многих исследованиях встает задача прогнозирования значений некоторой исходной переменной при заданных значениях факторов. В контексте факторного анализа это можно назвать также обратной задачей, задачей восстановления или интерполяции значений исходной переменной.
    Поясним это на примерах. Пусть в проекции измерений на факторную плоскость прослеживается некая явная функциональная зависимость между ними. Тогда законной будет постановка задачи прогнозирования этой зависимости в одном из двух направлений ее продолжения и проецирования этого прогноза на различные исходные переменные. Другим примером (даже в отсутствие упомянутой функциональной зависимости) является интерес исследователя к поведению исходных переменных в области промежуточных факторных значений, не зафиксированных в эксперименте. Это соответствует задаче интерполяции. Особый интерес представляет случай многомерных данных типа связных временных рядов, когда рассматриваемая постановка соответствует классической задаче прогнозирования временных рядов.
    Во всех этих случаях факторное прогнозирование имеет несомненные преимущества перед классическими методами прогнозирования и интерполяции средствами регрессионного анализа или с использованием математических моделей временных рядов. Действительно, в результате выделения главных факторов рафинируются основные закономерности, касающиеся исходных данных, и отсеиваются случайные и шумовые дисперсионные составляющие. Поэтому прогнозирование в пространстве главных факторов с последующим проецированием на исходные переменные не только более адекватно отражает многомерные закономерности, но и учитывает корреляционные связи между переменными. Тем самым в прогнозе учитывается зависимость не от одной переменной-параметра или от избранного набора переменных, но от всей многомерной совокупности переменных. Кроме того, получаемые прогнозы обладают важным свойством робастности, то есть нечувствительностью к случайным флуктуациям и выбросам.
    Методика факторного прогнозирования детально проиллюстрирована в [7].

    Вращение факторов. После выделения факторов многие источники рекомендуют произвести вращение избранных факторных векторов в определенном этими факторами подпространстве. Целью вращения провозглашается получение более просто интерпретируемой системы факторов (простая структура), при которой каждая переменная имеет большие нагрузки на малое число факторов и малые нагрузки на остальные факторы.
    Следует категорически заявить, что формулировка подобной цели в методическом плане принадлежит к области лженауки. Это называется подгонкой результатов. Представьте себе, что Уотсон и Крик начали бы вращать рентгеноскопические данные с целью облегчить себе жизнь и более быстро получить максимально простую модель ДНК. Тем не менее в связи с распространенностью этой ереси приведем некоторые сведения о вращениях [Многих сбивает также с толку кочующее по учебникам утверждение, что методы факторного анализа (см. ниже) дают решение с точностью до враще-ния факторов, из чего делается вывод, что вращение принципиально не меня-ет найденного решения. Однако факторное решение обеспечивает хорошее приближение общностей переменных (= сумма нагрузок) к исходным корреляциям, а общности переменных (в отличие от нагрузок) при вращении дей-ствительно не меняются. Но такое «обоснование» аналогично следующей наглядной ситуации. Пусть гражданин А платит за жилье миллион, а гражда-нин Б - тысячу. И мы говорим: давайте-ка повращаем ситуацию до наоборот, ведь общая-то квартплата от этого не изменится!].
    Методы вращения. Будем иметь в виду, что вращение осуществляется только в рамках выбранного подпространства, не затрагивая измерений специфических факторов. Так двумерное вращение в трехмерном пространстве состоит в повороте факторных осей X, Y вокруг неподвижной оси Z. Существует несколько "штатных" (широко распространенных) методов вращения.
    Наиболее употребительный метод варимакс обеспечивает разделение факторов за счет уменьшения числа переменных, связанных с каждым фактором.
    Метод квартимакс (к нему близок метод биквартимакс) имеет тенденцию к выделению генерального фактора, упрощающего интерпретацию за счет уменьшения числа факторов, связанных с каждой переменной. Метод эквимакс дает промежуточный эффект. Метод облимин реализует косоугольное довращение результатов варимакс-вращения. При этом факторы располагаются в пространстве исходных переменных не вполне перпендикулярно друг к другу с учетом их взаимной коррелированности. В случае малой коррелированности факторов, результаты облимин-вращения незначительно отличаются от метода варимакс.
    Следует также отметить, что при большом числе значимых факторов (5—7) результаты вращения сильно зависят от числа вращаемых факторов — различия здесь могут быть существеннее, чем различия между методами вращения.

    Об опасности вращения естественно-научных факторов. Операции вращения факторов начали применяться для данных опросного типа (преимущественно номинальные и ранговые данные), которые сами по себе глубоко субъективны, вариативны, неточны. Такие данные преимущественно распространены в гуманитарных исследованиях и к ним неприменимо понятие точности измерений, как это имеет место в случае данных, полученных с помощью измерительных приборов. Поэтому в результате вращения исследователь мало теряет в обоснованности выводов (поскольку сами исходные данные очень "рыхлые", "относительные"), но может получить более простую интерпретацию факторов. В отношении же естественнонаучных данных применение различных методов вращения факторов принципиально искажает характеристики и свойства изучаемых явлений вплоть до полного абсурда [У аудитории может возникнуть законный вопрос: а почему на это раньше никто не обратил наше внимание? На это мы зададим встречный вопрос: а где и как на это можно обратить внимание широкой научной, исследовательской и преподавательской аудитории? Оказывается - никак и нигде! Действительно, математические журналы отклонят такой материал по причине отсутствия теоретической новизны. Компьютерные журналы отклонят его по причине неинтересности и сложности для их аудитории. Единственно где его можно опубликовать - это в каком-нибудь малотиражном отраслевом сборнике, где его никто реально не прочтет].
    Откуда это пошло? Здесь следует вспомнить, что различные формы вращения были изобретены западными математиками, вовлеченными в масштабные государственные программы психологического и социального тестирования. Следующие в их фарватере системные аналитики без тщательной верификации в других областях приложения и необходимых оговорок включили вращения в свои статистические пакеты. Отсюда постепенно и развилась всеобщая "вращательная эйфория" [В этом плане показателен пример монографии [1], безусловно относящейся к фундаментальной классике. В разделе факторного анализа там всесторонне рассматривается пример измерения базовых физиологических показателей у 113 больных в отделении интенсивной терапии. Исходная компонентная структура подвергается различным методам вращения и каждый раз получается разное число главных факторов и разная их интерпретация. Тем самым физиологические механизмы изменяют свою работу в зависимости от метода вращения! Но этот абсурд нисколько не смущает авторов и они не делают ни одного предостерегающего комментария к столь странному пове-дению биологических законов].     Однако каждый критически мыслящий исследователь экспериментально легко может убедиться в том простом неприглядном факте, что различные методы вращения и изменение числа общих факторов часто дают несопоставимые результаты. Тем самым эти методы несомненно облегчают одну задачу: если очень хочется что-то доказать относительно исследуемого объекта, то часто удается подыскать для этого подходящий метод вращения.
    Так для нашего учебного примера метод варимакс осуществляет поворот первых двух факторов в рамках их двумерной плоскости (находящейся в трехмерном пространстве исходных переменных) примерно на 45°. Это же видно в повороте факторных нагрузок из сравнения рис. 5а и 11б. Тем самым проекции исходных переменных на факторные оси (а следовательно и предметный смысл факторов) кардинально меняются. Это же касается и собственных значений факторов: вместо подавляющего преимущества первого фактора (96,59% против 3,246%) после вращения мы имеем практическую эквивалентность двух главных факторов (55,34% и 44,53%). Очевидный абсурд состоит в том, что после вращения главный фактор "антропометрического масштаба" перестал действовать в мире сапиенсов! Изменение предметного смысла проявляется и в резких перемещениях объектов по факторной плоскости (ср. рис. 10а и 11а). На результатах последующей кластеризации объектов это не скажется, но результаты регрессионного анализа, групповых различий и содержательного сравнения объектов будут резко искажены. Фактически в результате вращения две факторные оси опять повернулись к двум исходным переменным, то есть результаты проведенной факторизации были полностью отменены!
 

а)

б)

    Другие методы факторного анализа. Кроме рассмотренного метода главных компонент существует еще и множество других алгоритмов выделения факторов: наименьших квадратов, максимального правдоподобия, центроидный, главных осей, альфа-факторный, анализ образов, канонический анализ Рао и др.
    К теоретическим недостатками метода главных компонент обычно относят то, что общности переменных (оценки корреляций) получаются автоматическим суммированием квадратов нагрузок по общим факторам без решения вопроса о приближении апостеорных коэффициентов корреляции (вычисленных по нагрузкам для сокращенного набора факторов) к исходным корреляциям переменных, что приводит к преувеличению факторных нагрузок. В этом плане кратко охарактеризуем некоторые из вышеупомянутых методов.
    Факторный анализ образов (Image Factoring) — это применение метода главных компонент к редуцированной матрице корреляций, у которой на диагонали стоят не единицы, а общности, оцененные как квадрат коэффициента множественной корреляции каждой переменной со всеми остальными. Однако результирующие общности также (но в меньшей степени) недооцениваются.
    Метод главных осей или главных факторов (Principal Axis Factoring) — это пошаговое продолжение анализа образов — на каждом последующем шаге в матрицу корреляций подставляются предыдущие значения общностей, пока не будет достигнут заданный уровень различий общностей между двумя последними шагами.
    Метод невзвешенных наименьших квадратов (Unweighted least Squares, Comrey, 1962) — по методу главных осей критерием остановки является достижение минимума среднеквадратичного отклонения исходных и вычисленных коэффициентов корреляции для внедиагональных элементов.
    Обобщенный метод наименьших квадратов (Generalized least Squares) — отличие критерия остановки состоит в присваивании переменной с большей общностью большего веса.
    Метод максимального правдоподобия (Maximum likelihood, D. Lawley, 1940) — оценка различий исходных и вычисленных коэффициентов корреляции производится по хи²-критерию. При получении результирующего значимого различия для М-факторной модели производится переход к М+1-факторной модели и т. д. Метод применим при условии многомерной нормальности исходных данных (тесты на многомерную нормальность очень чувствительны к отклонениям от теоретической модели).
    После того как были прочитаны предельно краткие выдержки с минимумом специальных терминов из более чем пространных теоретических рассуждений, уместно самому себе задать следующий риторический вопрос: способны ли на этой основе сделать сколько-нибудь рациональный выбор миллионы рядовых пользователей, не обремененных высокой математической ответственностью?
    Более того, при использовании различных методов факторизации соотношения оценок факторных нагрузок могут в ограниченных пределах меняться количественно (см. пример в [3]), но практически никогда качественно (на прямо противоположенные), то есть не затрагивая  содержательную интерпретацию факторов. Следует признать, что такие различия не принципиальны с учетом полной неопределенности статистической достоверности общих результатов факторизации. К тому же эта незначимая разница исчезает после вращения, методы которого приводят уже к кардинальным различиям в факторных нагрузках и в интерпретации.
    Для дополнительной проверки мы провели сравнение различных методов факторного анализа средствами пакета SPSS.12 на матрице 46 экономических показателей РФ за 48 месяцев 1996—1999 (см. разд. 14.4.3 в [7]). Вряд ли эти данные можно признать не удовлетворяющими основным требованиям факторного анализа или некоторым образом сингулярными. И вот что мы обнаружили интересного:

методы обобщенных МНК и максимального правдоподобия вообще отказываются работать с диагностикой "не был найден локальный минимум" (и какого же им такого уникального минимума не хватает?);

анализ образов дает точно такие же собственные значения, что и главные компоненты: 14, 9.62, 8.22, 3.7, однако в факторных нагрузках наблюдается полный абсурд: первый фактор, определяющий 30% дисперсии, имеет меньшие нагрузки, чем третий и четвертый, а восстановление собственных значений по факторным нагрузкам дает совершенно непонятное: 7.1, 5.47, 8.25, 9.12.

методы невзвешенных МНК и главных осей дают совершенно одинаковые результаты, незначительно от них отличаются результаты альфа-факторного анализа, при этом максимальные различия от главных компонент составляют 3-4% и лишь в 5-10% случаях.

    Планирование исследования. В заключение необходимо упомянуть о двух целевых направлениях факторного анализа: эксплораторный (разведочный — посмотреть, может быть что-нибудь обнаружится интересное) и конфирматорный (подтверждающий гипотезу). Второе направление анализа часто используется на завершающей стадии крупной работы и предполагает особые требования к планированию эксперимента по сбору первичных данных [8, 9].
    В первую очередь исследователь должен выработать гипотезу относительно того, какие факторы могли бы описывать предметную область. Статистически очень важно, чтобы экспериментальное исследование было достаточно широким и можно было бы выделить не менее пяти-шести гипотетических факторов, иначе будет трудно говорить об устойчивости решения. С другой стороны, потеря какого-то фактора, действительно участвующего (лежащего в основе, детерминирующего, связанного) в изучаемом процессе, может стать серьезным препятствием с точки зрения успешности исследования. Ошибки при измерении каких-либо важных факторов могут привести к неправильной трактовке очевидных взаимосвязей между измеряемыми факторами. Включение всех факторов, имеющих отношение к исследуемой области, это в первую очередь содержательная, а не статистическая проблема.
    Далее исследователь должен выбрать переменные для наблюдения. Для каждого гипотетического фактора следует предусмотреть пять или шесть первичных наблюдаемых переменных, которые позволят измерить фактор a "чистом" виде (исходя из предположения, что эти переменные детерминированы только этим фактором). Их называют маркерными переменными. Другими словами, маркерные переменные должны быть в высокой степени взаимосвязаны с одним и только одним фактором и иметь по нему высокие нагрузки вне зависимости от того, с помощью какого алгоритма выделялись и вращались факторы. Маркерные переменные четко определяют природу фактора. Добавление переменных, которые потенциально могут быть объяснены каким-то фактором, с тем чтобы более четко выявить его семантику, гораздо более эффективно, если этот фактор с самого начала был однозначно определен маркерными переменными.
    Следует учитывать также сложность переменной, характеризуемую количеством факторов, с которыми эта переменная коррелирует (взаимосвязана). Переменные разной сложности, включенные в исследование, могут "связываться" в факторы, имеющие очень мало общего с исследуемым процессом. Переменные одинаковой сложности могут "связываться" между собой (иметь высокий показатель взаимосвязи) именно по этой причине, а не потому, что они относятся к одному и тому же семантическому фактору. Оценка сложности переменных — это неотъемлемая часть процесса порождения гипотез о факторах и выбора переменных для измерения факторов.
    Очень важно также, чтобы показатели объектов, составляющих экспериментальную выборку, покрывали возможно более широкий спектр значений как по наблюдаемым переменным, так и по латентным факторам. Действительно, если все испытуемые имеют практически одинаковые значения по какому-то фактору, то взаимосвязь между наблюдаемыми переменными низка и фактор может не выделиться. Выбор объектов с ожидаемо высоким разбросом показателей по наблюдаемым переменным и латентным факторам — важная составная часть планируемого исследования.
    Следует также внимательно относиться к объединению для факторной обработки данных, полученных на нескольких выборках или на одной и той же, но в течение длительного временного интервала. Во-первых, объекты, различающиеся по какому-либо критерию (например, по социально-экономическому статусу), могут также характеризоваться различными факторами. Изучение групповых различий в большинстве случаев очень полезно для прояснения гипотезы. Во-вторых, структура латентного фактора может изменяться во времени для одних и тех же объектов (например, для испытуемых по мере получения ими полной информации и опыта участия в эксперименте). Исследование подобных различий также может быть очень полезным, а объединение результатов разных групп в одну матрицу может скрыть (а не выявить) различия. Если же на различных выборках действительно получаются аналогичные факторы, то их объединение даже желательно, ибо увеличивает статистическую устойчивость результатов.