
ТРАНСФИНИТНЫЕ МНОЖЕСТВА - ПРЕДЕЛЫ
ПОЗНАНИЯ
г
Кулаичев А.П., 2008-2014
ссылки при цитировании на одноименную
публикацию: журнал "Философия науки", №4, 2014, с.41-56. .  Download
PDF
Download
PDF

УДК 510.21+510.222+510.227
Аннотация.
Рассмотрены семантические проблемы познания бесконечных множеств. Показано
существование различных направлений воззрения на содержательные основания,
базовые понятия и структуру бесконечных множеств, ведущих к различным и
противоположным выводам. Тем самым в данной области в связи с конечностью
возможностей субстрата человеческого разума присутствуют определенные пределы
познания, в связи с чем различные точки зрения, доказательства и выводы
имеют право на равноценное сосуществование, подобно принципу дополнительности
Бора в физике.
Ключевые
слова: теория множеств, трансфинитные
множества, ординалы, кардиналы, счетность, математическая индукция, абсолютная
истина
1. ВВЕДЕНИЕ
Математика
издревле считалась высшим продуктом абстрактного человеческого мышления,
собранием или сокровищницей абсолютных, идеальных, неоспоримых истин. Однако
на рубеже XX века в истории математики произошло знаменательное, но малозамеченное
событие. До этого математика открывала или извлекала из неведомого хранилища
истины вышеупомянутого типа, подобные правилам умножения, квадратуре круга,
преобразованию Фурье и т.п. Но с последней четверти XIX века в математике
начали появляться теории и гипотезы. Кто-то может посчитать это просто
введением нового оборота речи, но это может быть и не так.
Действительно, теория представляет собой совокупность интуитивно или содержательно
обоснованных исходных положений, предназначенных посредством определенных
правил вывода логически убедительно объяснить некоторые свойства, закономерности
или явления внешнего или внутреннего мира. При этом для подобного объяснения
может существовать несколько различных теорий, и принятие той или иной
теории является следствием не ее абсолютной истинности, а предметом общественного
соглашения. То или иное социальное сообщество может предпочитать ту или
иную теорию и следовать ей в соответствии со свободой своего выбора. Такое
же положение имеет место и в отношении различных теорий бесконечных множеств.
Кроме того, степень общественного признания различных теорий в области
естественных наук определяется предсказательной адекватностью конкретной
теории, поскольку эти предсказания обычно доступны для последующей экспериментальной
проверки. Математика же не является наукой с возможностью экспериментальной
проверки положений той или иной теории в области бесконечных множеств.
Вместо экспериментальной проверки выводов математической теории единственным
критерием ее истинности остается непротиворечивость ее выводов в рамках
самой теории, а вовсе не наличие противоречий с выводами других теорий.
В такой ситуации на степень общественного признания той или иной теории
начинают оказывать влияние политические соображения и телеологические основания,
далеко не всегда совместимые с бесстрастным научным подходом к доказательствам.
Углубленное проникновение человеческого разума в область бесконечных множеств,
начавшееся в последней четверти XIX века вызвало целый ряд ограничений
на способы рассуждений, каждое из которых является не предметом абсолютной
истины, а предметом общественного соглашения. И некоторые современные преподаватели
и лекторы явно предупреждают об этом аудиторию в своих произведениях: «На
самом деле мы уже приблизились к опасной границе, когда наглядные представления
о множествах приводят к противоречию» [1, с.33], «Тут опять мы подходим
к опасной границе парадоксов и вынуждены выражаться уклончиво» [1, с.104].
Некоторые содержательные, в том числе и малоизвестные сложности и неоднозначности
в попытках человеческого разума осмыслить свойства бесконечных множеств,
выбор из которых становятся предметом общественного соглашения (ОС) вследствие
пределов познания абсолютной истины, мы попытаемся далее рассмотреть.
1. ПРОБЛЕМЫ 1-3 «ОМЕГА»
Как
известно, Георг Кантор начал свои работы по теории множеств с определения
или введения в математику ординальных чисел. Основополагающая идея основывалась
на работах математиков XVII-XIX вв., связанных с понятиями бесконечно малых
величин, пределов и бесконечных числовых рядов. Действительно, если для
бесконечного числового ряда вида n/(n+1), n** имеется недостижимый для
него предел, равный 1, и хотя этот ряд бесконечен, за ним по порядку непосредственно
следует единственное число 1. Именно эту аналогию и использовал Кантор
[2, с.293], когда предложил математическому сообществу считать, что за
натуральным рядом чисел по порядку непосредственно следует трансфинитное
или сверхконечное число *, которое является пределом для n** и которое
большее любого из натуральных чисел. А далее этот ряд трансфинитных порядковых
чисел естественным образом бесконечно продолжается *, *+1,..., *2, *2+1,...,
*m, *m +1,... точно также как и n/(n+1), 1, 1+ n/(n+1), 2, ..., m,
m+ n/(n+1), m+1, ... . Но здесь возникает ряд принципиальных проблем выбора
или предметов ОС.
Проблема
1 – соотношение неограниченно большого и бесконечного.
Как известно, Кантор строго разграничивал эти два понятия и неоднократно
подчеркивал это в своих работах, называя первое понятие несобственной бесконечностью,
а второе – собственной бесконечностью. [3, с.65]. Кантор также отождествлял
первое понятие с потенциальной бесконечностью, а второе понятие – с актуальной
бесконечностью [4., с.267], хотя дискуссии по соотношению этих двух категорий
бесконечности ведутся с древнейших времен до наших дней [5, 6]. Отмеченное
соотношение проявляется, в частности, в представлении рациональных чисел.
Так, рациональные дроби вида (2i-1)/(2n), i,n**, n*i, при i,n * * в любой
системе счисления (десятичной, двоичной и т.д.) имеют представление с неограниченно
большим, но не бесконечным числом значащих цифр. С другой стороны, дроби
вида (2i)/(2n+1) i,n**, n*i имеют представление не с неограниченно большим,
а с бесконечным числом значащих цифр.
Итак, * является пределом для натуральных чисел и большим, чем любое натуральное
число, поэтому * называется наименьшим бесконечным (least infinite, transfinite)
порядковым числом в отличие от предшествующих ему конечных порядковых чисел.
И здесь возникает первая смысловая проблема как предмет ОС: как бесконечное
множество, обозначаемое ординалом *, может соответствовать неограниченно
большому множеству натуральных чисел?
На подобные размышления наводит и теоретико-множественное определение порядковых
чисел: 0 = ? = {}, 1 = {0}, 2 = {0,1}, 3 = {0,1,3}, … . Здесь каждое
порядковое число означает множество предшествующих ему чисел, откуда можно
заключить, что ординал * следует понимать как обозначение множества предшествующих
порядковых чисел, т.е. как имеющего ту категорию неограниченно большого,
а не бесконечного.
Здесь прослеживается также важная связь с семантикой понятия натуральное
число. Натуральные числа предназначены для обозначения количества объектов,
существующих в том или ином смысле (in Nature), а не для обозначения феномена
несуществования объектов (out of Nature). То же относится и к семантике
понятия множество – от «много», что не включает понятие «ничего». Каждое
натуральное в этом смысле число обозначает только соответствующее натуральное
количество, которое соответствует его позиции в ряду 1,2,3,…, а не количество
предшествующих целых чисел, начиная с 0. Поэтому, если в определении порядковых
чисел исключить ?, то бесконечная категорийность * стала бы безальтернативной.
Но это уже является предметом ОС.
Рассмотрим в этом плане дроби вида (2i)/(2n+1)
i,n**, n*i, выражающиеся числами с бесконечным рядом значащих цифр. Пронумеруем
эти значащие цифры, и зададимся вопросом, как обозначить предел этой нумерации
или «сверхконечную» значащую цифру? – очевидно символом *, как пределом
множества n**. Отсюда также следует, что * относится к бесконечной, а не
к неограниченно большой категории.
К аналогичному выводу можно прийти и из рассмотрения сходящихся к пределу
числовых рядов, откуда и возникла идея *. Так числовой ряд n/(n+1), n**
сходится к пределу 1, который в свою очередь имеет эквивалентное обозначение
0.999… , включающее не неограниченно большое, а актуально бесконечное количество
значащих цифр. Отсюда и * следует понимать как категорию актуально бесконечного.
Тем самым здесь могут быть противоположные точки зрения и аргументы, выбор
из которых является предметом ОС.
Вместе с этим Кантор безальтернативно понимал * именно как категорию бесконечного
[7, с.283], цитируем: «Чтобы заранее исключить возможность этого смешения
[несобственного и собственного бесконечного], я обозначаю наименьшее трансфинитное
число знаком, отличным от обычного знака ?, соответствующего смыслу потенциально
бесконечного, а именно через *. Разумеется, этот знак * можно в известном
смысле рассматривать как предел, к которому стремится переменное целое
число ?, но только в том смысле, что * есть наименьшее трансфинитное порядковое
число, т. е. наименьшее твердо определенное число, которое больше, чем
все конечные числа ?.»
Проблема
2 – количественного аспекта ординальных чисел.
Если любое натуральное число представимо только конечным числом значащих
цифр, то ординал * является первым из ординалов, превосходящим любое из
натуральных чисел. Поэтому * может быть представлен только с бесконечным
числом значащих цифр. Подобные супернатуральные числа были введены в 1910
г. немецким математиком Эрнстом Стейницем, и они используются, в частности,
в некоторых разделах теории групп. Встает вопрос, как могут соотноситься
трансфинитные ординалы с числами Стейница? Здесь следует отметить два момента:
1) для чисел Стейница не определена операция сложения, следовательно на
их множестве исходно не определен порядок; 2) количественный аспект (мощность)
всех трансфинитных ординалов одинаков. Поэтому каждому из ординалов в его
численно-значащем выражении может быть сопоставлено все множество чисел
Стейница, мощность которого равна континууму. Тем самым здесь имеет место
определенная проблема соотношения счетности каждого ординала и несчетности
его множества его численно-значащего выражения.
С другой стороны, данный численно-значащий
аспект подтверждает бесконечную, а не неограниченно большую категориальность
ординала *.
Проблема
3 – порядкового места трансфинитных чисел
вида nw. Теоретико-множественное
доказательство порядкового положения трансфинитных чисел вида nw.следующее
[14]. Любое nw, например 2w,
является пределом бесконечно возрастающей последовательности натуральных
чисел 20, 21, 22, 23,.... или
подмножества натурального ряда, а пределом любогл бесконечно возрастающего
подмножества натурального ряда является w, поэтому
и порядковое место всех nw
совпадает с w.
На это «доказательство» можно привести, по крайней мере, два принципиальных
возражения.
1. Данное «доказательство» не является доказательством порядкового места
чисел nw, а является только
доказательством их эквивалентности трансфинитному числу w,
то есть их счетности. В противном случае точно таким же образом можно «доказать»,
что порядковые места всех ординалов wn
совпадают с w, поскольку каждый из них является
пределом бесконечно возрастающей последовательности натуральных чисел 1n,
2n , 3n, 4n,... .
2. Рассмотрим две бесконечные последовательности трансфинитных чисел: 1w,
2w, 3w,
4w,... и w1,
w2,
w3,
w4,
... . Очевидно, что пределом для этих двух последовательностей является
ординал ww. Поэтому следует вопрос:
как соотносятся порядковые места трансфинитной последовательности 1w,
2w, 3w,
4w,... с порядковыми местами
ординалов w1,
w2,
w3,
w4,...
.?
Отсюда можно сделать следующий вывод: существует бесконечное множество
бесконечных последовательностей трансфинитных чисел, например 1w,
2w, 3w,
4w,..., 1w+1,
2w+1, 3w+1,
4w+1,..., ..., 1w+1,
2w+1, 3w+1,
4w+1,... и т.д., которые не являются
ординалами. Тем самым теория ординальных чисел не охватывает всех трансфинитных
чисел.
2. ПРОБЛЕМЫ 4-6 «МОЩНОСТИ»
Далее Кантор перешел к развитию
теории кардинальных чисел, доказав две принципиальные теоремы: о несчетности
множества действительных чисел (далее - ТК1) и ее обобщение - о мощности
множеств всех подмножеств (ТК2). ТК1 доказывается знаменитым диагональным
методом Кантора и может иметь как негативную формулировку (доказательство
от противного или приведение к противоречию), так и позитивную (прямую)
формулировку (выдвинутую, в частности, самим Кантором [8, с.170]).
ТК2 доказывается на первый
взгляд несколько другим методом, посредством предположения о наличии биективного
(взаимно-однозначного) отображения элементов исходного множества на множество
всех его подмножеств (или булеан) с последующим опровержения этого предположения
посредством построения подмножества не принадлежащего такому отображению
(доказательство от противного, хотя исходное утверждение можно переформулировать
и для прямого доказательства). Однако здесь крайне важно, что применительно
к булеану натуральных чисел это вроде бы «биективно» ориентированное доказательство
ТК2 сводится к тому же диагональному методу ТК1, если его применить к бесконечной
матрице характеристических функций подмножеств . И «биективно» ориентированное
порождение не принадлежащего к этой биекции подмножества состоит в диагональной
инверсии нулей и единиц исходной матрицы характеристических функций для
бесконечного списка предлагаемого множества всех подмножеств.
Канторово диагональное
доказательство с самого начала вызывало и до сих пор вызывает многостороннюю
критику, современные аспекты которой достаточно подробно изложены в сборнике
статей [6]. В этой критике можно выделить, по крайней мере, три основные
проблемы.
Проблема-4
состоит в том, что на основании порождения одного единственного числа,
не входящего в любую предъявленную бесконечно счетную последовательность
действительных чисел, делается вывод о большей мощности множества действительных
чисел по сравнению с мощностью множества натуральных чисел, что является
доказательством на основании одного единственного контрпримера. Иными словами,
принятие этого доказательство требует применимости к бесконечным множествам
принципа исключения третьего, действующего для конечных множеств, что является
предметом ОС. Большинство из математического сообщества такого соглашения
придерживаются, несмотря на то, что применение принципа исключения третьего
к бесконечным множествам привело в свое время к многочисленным математическим,
логическим и семантическим парадоксам, прежде всего, в связи с явным или
неявным использованием квантора всеобщности (подробнее см. в [9, 10]).
Проблема-5
возникает вследствие непринятия закона исключения третьего в отношении
бесконечных множеств, поэтому принцип единственного контрпримера отвергается
и выдвигается требование доказательства, что мощность множества всех порожденных
контрпримеров имеет мощность, большую счетной мощности [11]. Отметим, что
количество контрпримеров зависит от системы счисления для представления
действительных чисел - так в случае использования двоичной системы счисления
для представления бесконечного перечня действительных чисел может быть
порожден только один контрпример.
С другой стороны, каждый контрпример можно добавить к исходному
перечню чисел и повторять диагональную процедуру. Но здесь возникает два
варианта, также являющиеся предметом ОС. Все зависит от того, куда мы решим
добавлять контрпримеры. Если добавлять их в начало перечня действительных
чисел, то каждый раз будем генерировать новые контпримеры. Если же первый
контрпример добавить в конец перечня, то есть на место w+1,
то никакого нового контрпримера не образуется, и будет получен тот же самый
контрпример.
Проблема-6.
Независимо от закона исключения третьего имеется еще один повод для критики.
При исходной постановке вопроса априорно не известно, какова мощность множества
действительных чисел. Пусть составлен перечень всех рациональных чисел,
которых счетное множество w,
а к нему добавим перечень всех алгебраических чисел, не совпадающих с рациональными,
которых тоже счетное множество w.
Тем самым мы получили не квадратную матрицу wхw,
а прямоугольную матрицу w2хw,
и диагональ этой матрицы закончится на позиции по горизонтали w,
а не на позиции w2.
Очевидно нельзя доказать, что диагональный контрпример, порожденный в первой
половине такой прямоугольной матрицы принадлежит или не принадлежит ее
второй половине. Итак, при исходной неопределенности о ширине матрицы перечня
действительных чисел диагональное доказательство будет нелегитимно.
3. ПРОБЛЕМА 7 МОЩНОСТИ КОНТИНУУМА
Рассмотрим альтернативы доказательства
счетности/несчетности континуума с использованием множества 2*. Эта идея,
вероятно, неоднократно возникла у прикладных математиков на рубеже 70-х
годов в результате расширяющегося внедрения ЭВМ в научные исследования
с программированием в двоичных машинных кодах и благодаря появлению первых
переводных монографий по теории графов. В частности, проблема счетности/несчетности
вершин бесконечного бинарного графа позднее упоминается в [12, с.255],
и подобный граф в несколько другом аспекте рассматривается в [13] (в зарубежных
публикациях можно также встретить наименование Cantor tree). Здесь
мы проиллюстрируем эту идею в модифицированном представлении бесконечной
«двоичное» пирамиды, в которой количество блоков на ее нисходящих уровнях
i=0,* последовательно увеличивается вдвое (рис.1):
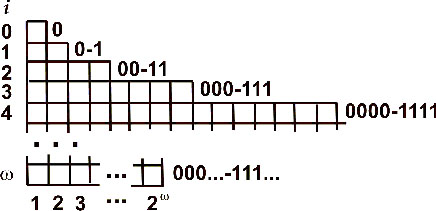
Рис.1. Бесконечная бинарно расширяющаяся пирамида
На каждом уровне блоки пронумерованы
в двоичной системе счисления (диапазон номеров приведен справа от уровней).
На каждом уровне i число блоков равно 2i
и их номера включают все комбинации нулей и единиц длиной i. На
уровне w число
блоков равно 2* и их номера включают все комбинации нулей и единиц длиной
w.
Если * представляет собой
не неограниченно большое, а бесконечное множество (Проблема 1), то на уровне
* номера блоков будут включать бесконечное число цифр 0, 1 и все их сочетания,
и эти номера являются счетным множеством. Отсюда следует, что множество
континуума будет счетным в противовес другому взгляду на бесконечные множества,
приводящему к доказательству теорем ТК1, ТК2. Тем самым здесь возникает
еще один предмет для ОС.
Двигаясь по уровню *
этой пирамиды и выписывая номера блоков получим следующую матрицу размером
2***:
0,
0 1 0 1 0 0 1 1 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
...
0 0 1 1 0 1 0 1 0 0 1 1 0 0 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
...
0 0 0 0 1 1 1 1 0 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
...
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
...
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
...
...
Прямое применение диагонального
метода Кантора к этой матрице (учитывая 2w=w)
дает число из всех единиц, являющееся в этой матрице последним, то есть
диагональное доказательство не доказывало бы теорему ТК1.
К этому примыкает и вопрос
о соотношении ординала w
и кардинала А0:
|2w|
= |w| = А0
< 2А0
= 2|w|
[14, с.72; 15, с.199]. По теореме ТК2 множество подмножеств любого множества
больше самого множества Р(А)=2A>A . С другой стороны,
для любого конечного множества MЙN
имеет место |2M|=2|M|, что согласно ТК2 нарушается
только начиная со всего множества натуральных чисел N: |2N|<2|N|.
Каким образом может быть |2w|<2|w|=2А0=с,
если |w| = А0?
Согласно определению Кантора [2, с.176], цитируем:
«Мощностью или кардинальным числом множества М мы называем то общее понятие,
которое получается при помощи нашей активной мыслительной способности из
М, когда мы абстрагируемся от качества его различных элементов m и от порядка
их задания». Отметим, что в множествах 2w
и Р(N)=2N все элементы имеют одинаковое качество, а порядок
элементов исходно не определен, что соответствует определению мощности
по Кантору, и мощности этих множеств должны совпадать. Поэтому соотношение
|2w|<2|w|
или |w|<|N|
может иметь место только в одном случае, а именно: множество 2w
или соответствующее ему отображение wЮ2
включает не все подмножества множества натуральных чисел, а именно – включает
только неограниченно большие, но не бесконечные подмножества. Именно тогда
2w будет
включать не все подмножества из N, а только подмножества из неограниченно
большого числа элементов, за рамками которых находится множество подмножеств
из бесконечного числа элементов, мощность которого равна континууму c=2А0>|2w|.
Чтобы это условие выполнялось, w
следует отнести к категории неограниченно большого, но не бесконечного,
что противоречит смыслу w
по Кантору и другим аргументам из раздела Проблема 1.
Тем самым здесь также
присутствует несколько проблем выбора или предметов ОС.
4. ПРОБЛЕМА 8 СЧЕТНОСТИ ww
(1). Ординалы
или множества ординального типа кроме обычных атрибутов, таких как мощность
и вполне упорядоченность, обладают также и определенной структурой,
поскольку состоят из последовательных отрезков. И точки зрения на структуру
ординалов могут быть различными. Так в традиционной интерпретации ординал
ww
определяется как сумма или объединение счетного w-числа
ординалов предшествующих степеней
wi,
откуда ww также полагается быть счетным,
цитируем по [7, с.70]: «ww является
счетным постольку, поскольку ww
= lim wi = lim{w1,
w2,
w3,…}
есть число, которое в силу равенств 1+w = w,
1+w+w2 = w(1+w)
= w2 и т.д. может быть записано в виде: ww
= 1+w+w2+…
= ».
Однако здесь
совершенно упускается из виду, что суммирование ординалов в порядке их
возрастания слева направо тождественно равно последнему справа (наибольшему)
ординалу вследствие некоммутативности операции сложения для ординалов.
Поэтому вышеприведенное выражение для ww
является не доказательством, а тавтологией ww=ww.
Можно найти
и альтернативное рассуждение, цитируем по [6, с.259]: «Например, a
= w2+w5+9
является разложением числа a по основанию w.
Чтобы разложить то же число по основанию 2, достаточно заметить, что w
= lim 2n = 2w. Тогда w2
= (2w)2
= 2w2, w5
= 2w+2+2w,
откуда a = 2w2+2w+2+2w+23+20.
Тем же способом получаем ww = 2(w^2)
». Однако продолжая эти преобразования с учетом w2
= 2w2 = 4w
= w, получаем «доказательство» ww
= 2(w^2) = 2(4^w)
= 2w = w.
Этот взгляд
на структуру ww существенно отличается
от предыдущего, и оба они противоречат общепринятому описанию ординалов
в нормальной форме Кантора [4, с.93]. Кроме того, в обоих случаях имеют
место чисто формальные манипуляции с символами, а не содержательное рассмотрение
вопроса, что нередко подвергается научной критике [1]. При этом сомнительно,
что подобные формальные преобразования применимы к любым ординалам, включая
и их трансфинитные степени, поскольку многие другие свойства операций с
конечными числами не переносятся на ординалы, например: 1+w№w+1,
2w№w2 и т.п. Отметим также, что подобные формальные,
индуктивные «доказательства» можно и далее преумножать, например: поскольку
2w = 4w
= … = nw = w
и ww = lim nw,
то ww = w.
(2).
Кроме того, хорошо известно, что на вполне упорядоченных отрезках ординалов
{a,...,b,...,c}
многие свойства и формулы P(b), действующие
для всех b<c,
не переносятся на предельный ординал c. Примерами
таких «непереносимых» свойств на отрезке {1,2,3,..., w}
для предела w являются: Q(n) -
«n есть конечнозначное число», но ШQ(w);
S(n)
– «n+1=1+n», но ШS(w);
R(n)
– «(n+1)/n>1», но ШR(w)
и многие другие. Подобные «непереносимые свойства» имеют место и для ординалов
трансфинитных степеней. В таких ситуациях доказательство P(c)
должно производиться неиндуктивными средствами, что касается и свойства
«ординал c является счетным».
(3).
В этом плане известно и третье альтернативное рассмотрение структуры ww
(восходящее к Г. Кантору для случая w2):
ww=Uwni
, i=1,ww для любого n,
то есть ww является не w-объединением
ординалов, а ww-объединением, что
влечет совершенно другие выводы. Рассмотрим последнюю альтернативу последовательно.
Первый трансфинитный
ординал w обозначает множество натуральных чисел,
которое счетно по определению. Ординал w2 является
предельным для множества 1, 2, 3, 4, ..., w,
w+1,
w+2,
w+3,...,
и доказательство его счетности производится прямым переупорядочиванием
элементов этого множества, в результате чего она сводится в одной счетной
последовательности 1, w, 2, w+1,
3, w+2, 4,
w+3,...
. Такой же метод применим и для последующих ординалов w3,
w4,
w5,
... .
Для ординала
w2,
являющегося пределом последовательности
w, w2,
w3,
..., вышеуказанный метод прямого переупорядочивания неприменим, и доказательство
его счетности (в его представлении как w2=Uwj,
j=1,w)
производится посредством перенумерации его элементов с использованием предложенной
Кантором функции [3, с.34], которая впоследствии получила наименование
функции сопряжения (pairing function):
p(i,
j) = 0.5(i+j)( i+j+1)+j,
(1)
где: p(i, j)
– новый (натуральный) порядковый номер элемента;
i – порядковый номер элемента в множестве wj;
j – номера множества wj.
Этот процесс
в современной литературе иллюстрируется контрдиагональным пересчетом элементов
w2,
представленных в виде двумерной бесконечной матрицы.
Для ординалов
последующих степеней wn соответствующие
множества представимы элементами n-мерных бесконечных матриц
wn=Uwjk...n,
j,k,…,n=1,w.
контрдиагональный
пересчет элементов которых описывается обобщением упомянутой функции сопряжения,
получившем название кортежной функции Кантора (tuple function) [19], определяемой
рекурсивной формулой:
p(n)(i,
j, k,...,n) = p(p(n-1)(
i,
j, k,...,n-1),n).
(2)
Использование такой кортежной функции аналогично пересчету элементов
множества wn
по n-1–мерным контрдиагональным гиперплоскостям в представляющей
множество *n n–мерной матрице.
Следуя такому представлению
можно придти к двум утверждениям.
Утверждение-1.
Множество ординального типа ww
несчетно.
Доказательство.
(1). Каждая
контрдиагональная гиперплоскость в матрице ww
имеет размерность ww-1, то есть ту
же самую ww-размерность, что и ww.
Поэтому уже на первой контрдиагонали проблема нумерации ее элементов возвращается
к исходной проблеме нумерации множества ww
и так далее бесконечно неразрешимо.
(2). Для ww,
являющегося пределом для ординалов wn
при n=w, принимая во внимание ww-1=ww,
получаем выражение кортежной функции:
p(w)(i,
j, k,...,w) = p(p(w-1)(i,
j, k,...,w-1), w)
= p(p(w)(i,
j, k,...,w), w),
(3)
что является неразрешимым уравнением. Это показывает,
что для ww кортежная функция не существует
и нумерация элементов ww не возможна.
Тем самым утверждение-1 доказано с двух точек зрения.
Отметим также,
что доказательство (2) утверждения-1 не распространяет индуктивно
свойство счетности предшествующих (натурально-числовых) степеней wn
на их
ww предел. Наоборот, оно ясно
доказывает, что восходящее к Кантору правило нумерации элементов wn
ординалов не может быть распространено на их ww
предел.
Утверждение-2.Мощность
множества типа ww равна мощности
множества всех подмножеств натурального ряда чисел или мощности континуума
2А0=с.
Доказательство.
Множество всех
подмножеств натуральных чисел включает: все подмножества из одного числа,
все подмножества из двух чисел и так далее, до всех подмножеств из бесконечного
количества натуральных чисел.
С другой
стороны, все подмножества из двух чисел представимы в двумерной бесконечной
матрице w2, первая строка которой
содержит подмножества из одного элемента:
{1}
{2} {3} {4} {5} ...
{1,2} {1,3} {1,4} {1,5}
{1,6} ...
{2,3} {2,4} {2,5} {2,6}
{2,7} ...
{3,4} {3,5} {3,6} {3,7}
{3,8} ...
{4,5} {4,6} {4,7} {4,8}
{4,9} ...
...
... ... ...
... ...
Все подмножества
из трех чисел представимы в виде 3-мерной бесконечной матрицы w3,
у которой первая плоскость содержит подмножества из одного и двух элементов.
И так далее до множества всех подмножеств натуральных чисел, которое представимо
бесконечной матрицей с бесконечным числом измерений, которая соответствует
ординалу ww.
Тем самым теорема
доказано.
Следствие
1. Из данной теоремы вытекает обоснование гипотезы континуума,
поскольку во всей предшествующей и монотонной последовательности трансфинитных
счетных ординалов w,..., w2,...,
w3,...,
wn,...
ординал ww является первым несчетным
ординалом, и он соответствует кардинальности множества всех подмножеств
натуральных чисел 2А0=с.
Тем самым его кардинальность является первой после А0,
то есть А1.
Следствие 2.
Последующие ординалы восходящего ряда w-степеней
от ww представляют множества подмножеств
ординалов предыдущих w-степеней от ww,
тем самым ординалы w(w^w),
w(w^(w^w)),
... соответствуют кардинальным числам А2, А3,
А4,…
. Так в случае кардинала А2=2А1
следует применить доказательство теоремы к трансфинитной матрице размера
ww
вместо w и с числом измерений ww
вместо w. Эта матрица и представляет ординал
w(w^w)
и так далее.
Таким образом, различные
взгляды на структуру множества ww
приводят к ряду не совпадающих выводов, выбор из которых является предметом
ОС, а не императивом абсолютной истины.
5. ЗАКЛЮЧЕНИЕ
Пожалуй,
попытки содержательного и философского осмысления чистыми математиками
исходных понятий теории множеств закончились, главным образом, на Георге
Канторе и в меньшей степени – на его современниках. При этом последние
большей частью сконцентрировались на идеологических и логических дискуссиях
не по исходным теоретико-множественным понятиям, а по развиваемым ими различным
направлениям в основаниях математики, определенных телеологической установкой
- избавление от парадоксов.
Подавляющее большинство современных математиков подчас крайне жестко и
даже непримиримо избегает обсуждения содержательных, философских и логических
оснований своей науки. Это не в последнюю очередь определено тем, что с
середины ХХ в. в математике усиливается тенденция к углубляющейся формализации
и изоляции различных, даже очень близких разделов, когда работающие в них
математики перестают понимать творчество друг друга [10, с.482-530, 20].
Одним из редких, но показательных примеров в этом плане является статья
главного редактора престижного междисциплинарного журнала «Бюллетень символической
логики» [21]. В самом начале этой статьи, предназначенной рассмотреть и
опровергнуть основные направления критики теории множеств, много лет письменно
поступающие в редакцию, предупреждается, что никаких конкретных примеров
рассмотрено не будет, поскольку раскрытие неопубликованных материалов из
частной переписки неоднократно становилось предметом судебных исков за
нарушение авторских прав. Поэтому все «опровержения» в статье носят отвлеченный,
умозрительный, неконкретизированный характер с рядом пространных привлечений
не математических, а отрывочных психологических обоснований.
Кантор
утверждал, что «сущность математики заключается именно в ее свободе» [3,
с.80], добавляя «Математика в своем развитии совершенно свободна и связана
лишь тем само собой разумеющимся условием, что ее понятия должны быть непротиворечивы,
а также должны находиться в неизменных, установленных определениями отношениях
к образованным раньше и уже имеющимся налицо испытанным понятиям». Действительно,
математика свободна изобретать и исследовать свойства любых идеальных объектов,
создавать различные аксиоматические системы для описания одних и тех же
объектов и исследовать формальные следствия из таких систем. Однако человеческий
разум в отношении бесконечных множеств всегда будет волновать не столько
формальная сторона различных математических построений, сколько их содержательные
и философские основания.
Выше были продемонстрированы многочисленные ограничения познавательных
возможностей человеческого разума в отношении бесконечных множеств. Эти
ограничения, вероятно, определены конечностью самого мозга как субстрата
человеческого разума. Его «элементная база» включает: конечное число нейронов
(@1011), конечное число связей этого
множества нейронов с другими нейронами (@1015),
конечное число состояний всех этих «элементов» (@2(10^15)),
действующих по принципу двоичной логики, и конечность комбинаторики этих
состояний как множества отображений их на самое себя (@2(10^15)
-> 2(10^15)) или множество подмножеств из 2(10^15).
Отсюда следует, что попытки человеческого мозга осознать свойства бесконечности,
вероятно, обречены быть столь же бесконечными, как и сама бесконечность,
а различные точки воззрения на трансфинитные множества, доказательства
и их результаты без претензий на выражение абсолютной истины обязаны равноправно
сосуществовать подобно принципу дополнительности Нильса Бора в физике.
ЛИТЕРАТУРА
1. Верещагин Н.К., Шень А. Лекции
по математической логике и теории алгоритмов. Часть 1. Начала теории множеств.
Изд. 2-е.— М.: МЦНМО, 2002.
2. Кантор Г. К обоснованию
учения о трансфинитных множествах (1895). В кн.: Кантор Георг. Труды по
теории множеств.— М.: Наука, 1985.
3. Кантор Г. Основы общего
учения о многообразия. Математически-философский опыт учения о бесконечном
(1883). В кн.: Кантор Георг. Труды по теории множеств.— М.: Наука, 1985.
4. Кантор Г. О различных
точках зрения на актуально бесконечное (1888). В кн.: Кантор Георг. Труды
по теории множеств.— М.: Наука, 1985.
5. Петров Ю.А. Логические
проблемы абстракций бесконечности и осуществимости. М.: Наука, 1967.
6. Математика и опыт. Сб. статей
под ред. А. Г. Барабашева. — М.: МГУ, 2003.
7. Кантор Г. К учению о трансфинитном
(1887). В кн.: Кантор Георг. Труды по теории множеств.— М.: Наука, 1985.
8. Кантор Г. Об одном
элементарном вопросе учения о многообразиях (1890-91). В кн.: Кантор Георг.
Труды по теории множеств.— М.: Наука, 1985.
9. Бурова И.Н. Парадоксы теории
множеств и диалектика. — М.: Наука, 1976.
10. Клайн М. Математика. Утрата
определенности. — М.: РИМИС, 2007.
11. Зенкин А.А. Ошибка Георга
Кантора. Вопросы философии, 2: 165-168, 2000.
12. Кулаичев А.П. Компьютерный
контроль процессов и анализ сигналов. — M.: Информатика и компьютеры, 1997.
13. Зенкин Александр А., Зенкин
Антон А. Насквозь дырявый континуум: от языка абстракций к языку образов
и обратно. В сб. "Языки науки – языки искусства". — М.: "Прогресс-Традиция",
172-179, 2000.
14. Хаусдорф Ф. Теория
множеств. — М.: Либроком, 2007.
15. Potter Michael. Set Theory
and its Philosophy. A Critical Introduction. Oxford University Press, N.Y.
2004.
16. Куратовский К., Мостовский
Л. Теория множеств. М.: Мир, 1970.
17. Арнольд В.И. Математическая
дуэль вокруг Бурбаки. Вестник РАН, 72(3): 245-250, 2002.
18. Кантор Г. К учению о многообразиях
(1878). В кн.: Кантор Георг. Труды по теории множеств.— М.: Наука, 1985.
19. Lisi M. Some remarks on
the Cantor pairing function. Le Matematiche, 62(1): 55-65, 2007.
20. Бурбаки Н. Архитектура
математики. Математическое просвещение, 5: 99-112, 1960.
21. Hodges Wilerid. An editor
recalls some hopeless papers. The Bulletin of Symbolic Logic, 4(1):1-16,
1998.


![]() Download
PDF
Download
PDF![]() Download
PDF
Download
PDF
![]()