ДИДАКТИКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
г Кулаичев А.П.
ссылки при цитировании: Кулиичев. Методы и средства комплексного анализа данных. ИНФРА-М, 2006, 512 с, С.114-122

     Проверка гипотез. Поскольку статистика как метод исследования имеет дело с данными, в которых интересующие исследователя закономерности искажены различными случайными факторами, большинство статистических вычислений сопровождается проверкой некоторых предположений или гипотез об источнике этих данных.

     Нулевая гипотеза. Основное проверяемое предположение называется нулевой гипотезой Н0 и обычно формулируется как отсутствие различий, отсутствие влияния фактора, отсутствие различия значения выборочной характеристики от заданной величины (например, нуля) и т. п. Как правило, Н0 не является для исследователя содержательной гипотезой, т. е. предметом и целью доказательства.

     Альтернативная гипотеза. Другое проверяемое предположение (не всегда строго противоположное или обратное первому) называется конкурирующей или альтернативной гипотезой Н1. Обычно профессиональный интерес исследователя сводится именно к верификации альтернативной гипотезы.

     Ошибки 1- и 2-го рода. При проверке статистических гипотез возможны ошибки (ошибочные суждения) двух видов:

  1. 1. Можно отвергнуть нулевую гипотезу Н0, когда она на самом деле верна — это называется ошибкой первого рода, а вероятность такой ошибки a называется уровнем значимости нулевой гипотезы.
  2. 2. Можно принять нулевую гипотезу Н0, когда она на самом деле не верна — это называется ошибкой второго рода и вероятность такой ошибки обозначается b.
     Таким образом, вероятность правильного принятия гипотезы Н0 будет равна 1-a (эта вероятность называется доверительной вероятностью), а вероятность правильного принятия гипотезы Н1 будет равна 1-b (эта вероятность называется мощностью или чувствительностью критерия, характеризуя его способность отклонять Н0, когда она не верна).
     Оптимальная величина a (критический уровень значимости) должна удовлетворять двум противоречивым требованиям:
  1) она должна быть достаточно мала, чтобы обеспечить высокое общественное доверие к выводу об отклонении Н0;
  2) но она должна быть достаточно велика, чтобы реже допускать ошибки 2-го рода.
При этом вероятность ошибки b уменьшается при увеличении значения a, а для фиксированного значения a: а) при увеличении объема выборки; б) при уменьшении выборочной дисперсии.

     Статистические критерии. Для проверки конкретной нулевой гипотезы строится статистический критерий T — некоторая вычислительная функция от исходных данных, по значению которой проверяется нулевая гипотеза.
     Для каждого критерия в области его значений вычисляется и табулируется функция вероятности ошибки первого рода a = f (T,N), которая зависит также от одной или нескольких переменных N, называемых число степеней свободы, обычно связанных с размерами и числом анализируемых переменных (выборок).
     Табулирование значений статистического критерия состоит в следующем. Пусть имеется некая большая и нормально распределенная совокупность измерений, характеризующаяся средним значением М1 и какой-то дисперсией. Будем выбирать из этой совокупности случайным образом два подмножества размером в 10 измерений (например, для совокупности их 200 измерений таких различных подмножеств будет 1027). 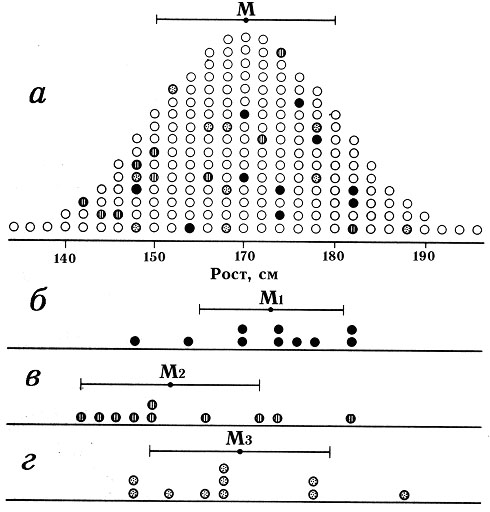Теперь вычислим для всех пар полученных подмножеств (а они в той или иной степени будут различаться в своих выборочных средних) значения некоторого криткрия (например, t-критерия Стьюдента) и построим функцию плотности вероятности распределения этих вычисленных значений (рис. 1, а, по горизонтальной оси — t-значения). Это и будет распределение плотности вероятности нулевой гипотезы, когда она верна.

 
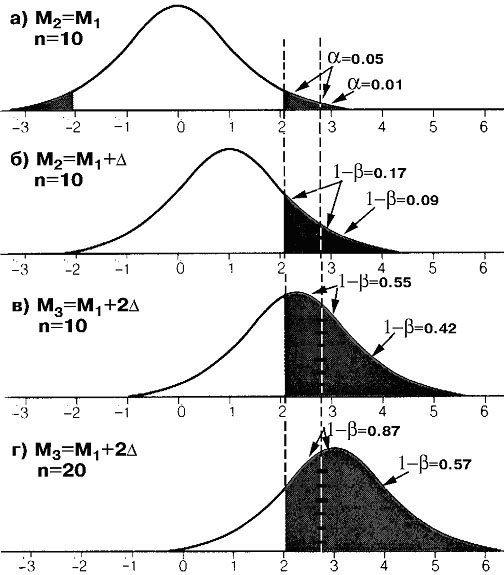
Рис. 1. Соотношения вероятностей ошибок первого и второго рода

     Мы видим, что при равенстве средних двух выборок t-значение равно нулю, чем больше разность средних (по модулю), тем больше t-значение (по модулю), но меньше вероятность такого расхождения. На рис. 1, а показано, что только 5% из всех пар выборок имеют разность средних значений, оцениваемых t-значениями, большими 2,1 (зачерненная область). И только 1% из всех пар выборок имеют разность средних значений, оцениваемых t?значениями, большими 2,87 (хвостик за второй штриховой линией). Это и будут критические t-значения при a = 5% и a = 1% для нулевой гипотезы, когда она верна. То есть при выбранном критическом уровне в a-проценте случаев нулевая гипотеза будет отвергаться, хотя она и верна (ошибка первого рода).
     Такое статистическое моделирование методом Монте-Карло производится для всех возможных сочетаний размеров двух выборок (степеней свободы n, m), в результате чего строится таблица критических значений (в данном случее t-критерия) в зависимости от соотношений степеней свободы n, m и для различных значений a = 0.05, 0.01, ... Такие таблицы для разных критериев публикуются в учебниках по статистике.

     Проверка нулевой гипотезы. Если вычиленное исследователем значение критерия для двух экспериментальных выборок размером n, m больше критического из таблицы для некоторого a, то нулевая гипотеза может быть отвергнута на этом уровне значимости.
Компьютерные программы используют аналитические аппроксимации для расспределений статистических критериев, что позволяет для проверяемых выборок сразу вычислить P — уровень значимости нулевой гипотезы (или выборочную оценку вероятности a) и тем самым решить вопрос о принятии или отвержении нулевой гипотезы на уровне P<a.
     Трактовка вычисленной значимости P включает следующие градации:
P > 0,1 — принимается Н0 и делается вывод: «статистически достоверные различия не обнаружены»;
P < 0,1 — неопределенность в отношении Н0 с выводом: «возможны различия на уровне статистической тенденции»;
P < 0,05 — значимое отклонение Н0 с выводом: «обнаружены статистически достоверные различия»;
P < 0,01 — отклонение Н0 с выводом: «различия обнаружены на высоком уровне статистической значимости»;
     Критический уровень значимости a = 0,05 рекомендуется для небольших выборок, когда велика вероятность ошибки 2-го рода. Для больших выборок (более 100 элементов) порог отклонения Н0 полезно снизить до 0,01.
     Ограничения. Отметим, что для вычисления уровня значимости статистик критериев в компьютерных программах используются аналитические аппроксимации, дающие хорошие результаты (точность до трех значащих цифр) для больших выборок, включающих более 10–15 элементов. Кроме того, эти формулы удовлетворительно аппроксимируют соответствующие статистические распределения в области значений 0,001<P<0,5. В области же других значений P они могут давать весьма приблизительные оценки. Однако это не является серьезным недостатком — при получении больших или малых значений P совершенно ясно, можно или нельзя принимать нулевую гипотезу.

     Соотношения вероятностей ошибок. Вернемся к рис. 1. Пусть теперь имеется другая большая совокупность измерений с такой же дисперсией, но отличающаяся своим средним значением М2 от М1 на некую условную величину D. Будем теперь выбирать случайным образом подмножества по 10 элементов из одной и из другой совокупности и сравнивать эти выборки попарно по t-критерию. Полученная в результате функция распределения t-значений будет соответствовать альтернативной гипотезе, когда она верна (при реальной разности средних D).  Эта функция, будет иметь определенное смещение (рис. 1, б) относительно случая отсутствия различия средних (рис. 1, а).
     Как видно из рис. 1, б, при выбранном уровне значимости нулевой гипотезы a = 5% только для 17% подмножеств (это чувствительность критерия 1-b) будет принята альтернативная гипотеза различия средних, а для a=84% случаев будет принята нулевая гипотеза, хотя она не верна (ошибка второго рода). При снижении же уровня значимости нулевой гипотезы до a=1%, чувствительность критерия к различиям падает до 9% подмножеств, а ошибка второго рода соответственно возрастает до 91%.
     Если теперь повторить вышеуказанную процедуру для другой совокупности измерений, которая отличается по своему среднему значению М3 от М1 на величину 2D, то получим функцию распределения t-значений, еще больше сдвинутую вправо (рис. 1, в). Тогда при a=5% уже для 55% подмножеств будет принята альтернативная гипотеза, т. е. чувствительность критерия повысится.
     Если же затем увеличить еще и объем извлекаемых подмножеств вдвое (до 20 элементов) и повторить процедуру, то получим функцию распределения, еще более сдвинутую вправо (рис. 1, г), и для a=5% получим чувствительность в 87% от всех пар сравниваемых подмножеств.
     Если же теперь взять другие совокупности, дисперсия которых в два раза меньше рассмотренных, то все функции распределения по сравнению с рис. 1 сожмутся в Sqrt(2)=1,44 раза относительно своих линий симметрии («колокола» уменьшат свой разброс), критические границы a соответственно сдвинутся влево, а зачерненные области принятия альтернативных гипотез расширятся с уменьшением ошибок второго рода.
     Аналогичный эффект будет наблюдаться для подмножеств в 10 элементов, если мы применим другой критерий сравнения различий, обладающий большей чувствительностью.

     Направленные и ненаправленные гипотезы. Статистические гипотезы могут быть направленными или односторонними (например, Н1:r>0 — «коэффициент корреляции больше нуля» или Н1:M1>M2 — «среднее значение выборки 1 больше среднего значения выборки 2») и ненаправленными или двусторонними (например, Н1:r<>0 или Н1:M1<>M2). Тип используемой альтернативы зависит от метода проверки гипотезы. Однако от типа альтернативы зависит расположение критической области и уровень значимости нулевой гипотезы. Так распределение значений критерия проверки однонаправленной гипотезы (рис. 5.4, а) имеет одну критическую область, а распределение значений критерия проверки ненаправленной гипотезы (рис. 5.4, б) имеет две критические области. Соответственно для одного и того же значения критерия t (рис. 5.3) соответствующий уровень значимости для однонаправленной гипотезы будет в 2 раза меньше, чем для ненаправленной гипотезы.

 
а — направленная гипотеза;                 б — ненаправленная гипотеза
Рис. 2. Критические области двух типов статистических гипотез (при одном выборочном значении t-критерия уровни значимости P1, P2 отличаются в 2 раза:

Проверка множественных нулевых гипотез

     Часто конкретный статистический метод используется для проверки нескольких статистических гипотез, по результатам которых делается общее заключение. Это относится к многим методам: к критериям парных выборочных различий, проверке отличия значения показателя от нуля (например, коэффициентов корреляции), вычислению доверительных интервалов, дисперсионному анализу и т.п. Типичный пример: имеется n выборок и между всеми парами (число таких пар m=n(n-1)/2) проверяются нулевые гипотезы об отсутствии статистических различий (например, в средних значениях) на критическом уровне значимости a. Однако в этом случае должен использоваться не уровень значимости одной нулевой гипотезы a, а уровень значимости множественных нулевых гипотез am, где m — число совместно проверяемых нулевых гипотез.

     Теоретическое обоснование. Критический уровень значимости a есть вероятность отвергнуть нулевую гипотезу, когда она действительно верна (ошибка первого рода). Если же совместно проверяются m нулевых гипотез, и они действительно верны, то в среднем будут неправильно отвергаться ma из них. Так, если a=0.05, то среди 20 совместно проверяемых нулевых гипотез (когда все они действительно верны) будет в среднем отвергаться одна из них (20*a*100%=100%). Чтобы в такой ситуации неправильно отвергать a*100% верных нулевых гипотез, при проверке каждой нулевой гипотезы следует использовать критический уровень значимости am=a/m. Это называется поправкой Бонферрони. При этом иногда рекомендуется также коррекция числа степеней свободы: nm=nm/2, где n — исходное число степеней свободы; m — число сравниваемых выборок.
     Можно рассуждать и иначе. В подобной ситуации вероятность правильного принятия всех m нулевых гипотез равна (1-a)m. Вероятность же неправильного отвержения хотя бы одной из них равна 1-(1-a)m. Нужно же, чтобы эта вероятность равнялась a при некотором скорректированном значении am проверки каждой из множественных гипотез: a=1-(1-am)m. Отсюда определим значение am=1-(1-a)1/m. Эта величина называется поправкой Шидака (Sidak), и она дает значение am, незначительно большее, чем поправка Бонферрони.
     Метод Холма: упорядочим выборочные уровни значимости m проверяемых нулевых гипотез по увеличению их значений p1<p2<...<pm, тогда i-я нулевая гипотеза из такой упорядоченной последовательности принимается, если pi<a/(m+1-i). Этот метод более «мягок» при небольшом числе гипотез с большим процентом исходно принятых альтернативных. Например, пусть проверяемые 4 нулевые гипотезы имеют знчачимость 0.01, 0.01, 0.02, 0.05. Критерий Бонферрони отвергнет две из них, а метод Холма – все.
     В качестве других подходов к данному вопросу предложены критерии Ньюмена-Кейлса, Тьюки, Даннета, Фишера, Хауэлла и другие (подробнее см. в [7]).

     Критика отмечает, что рассмотренные поправки при большом числе проверяемых гипотез чрезмерно жестко ограничивает вероятность принятия альтернативных гипотез. Действительно, все они ориентированы на уровень значимости нулевой гипотезы (false positives), а не на значимость альтернативной гипотезы  (false negatives, ошибка второго рода, которая однако нетабулируема).
     Нет также единого мнения по вопросу, что считать совокупностью совместно проверяемых гипотез (семейством, a family of hypotheses) Обычно считается, что коррекция am необходима, если после проверки m гипотез делается общий вывод о выявленных в этой совокупности различиях. Если же анализируется несколько совокупностей и выводы делаются по каждой из них отдельно, то для каждой совокупности используется своя поправка. Иначе возникает абсурдная ситуация: сегодня мы проверяли m гипотез, используя уровень значимости a/m, завтра мы проверяем k других гипотез и должны использовать уровень значимости a/(k+m), а также перепроверить на этом уровне вчерашние m гипотез?!   Ко всему прочему, с увеличением размера выборки ошибка среднего приближается к нулю, тогда как стандартное отклонение приближается к оцениваемому генеральному значению.

     Для уменьшения ограничений, накладываемых вышерассмотренными поправками возможны следующие варианты: 1) уменьшение числа совместно проверяемых гипотез; 2) при проверке выборочных различий разбиение выборок на группы и выявление межгрупповых различий методом двухфакторного дисперсионного анализа. В первом случае проверяются различия только между теми выборками, разности средних значений (или других числовых показателей) между которыми превосходят выбранный уровень. Во втором случае за счет увеличения степеней свободы существенно снижается выборочные уровни значимости нулевых гипотез для межгруппового фактора, одновременно значительно снижается число проверяемых множественных гипотез.

     Использование поправки Бонферрони или ее аналога в настоящее время является обязательным международным требованием. Игнорирующие это правило работы не принимаются к публикации в зарубежных научных журналах.

Природа статистических ошибок

     Статистические ошибки проистекают из-за конечности и ограниченности объема данных, предназначенных для анализа, и вероятность их возникновения уменьшается с увеличением размеров выборки. Пусть, например, создатели лекарственного препарата полагают, что его эффект возрастает пропорционально принятой дозе. Для проверки они назначают пяти пациентам разные дозы препарата и по полученным результатам строят график (рис. 3, а), на котором зависимость видна невооруженным глазом. Когда же препарат поступает в свободную продажу, его начинают принимать все больше людей в надежде улучшить свое самочувствие. По более представительной выборке видно, что связь лечебного эффекта от дозы не прослеживается (рис. 3, б, черными кружками отмечены данные первоначальных испытаний).

     Проверка статистических гипотез как раз и дает средства оценки вероятности получения столь «непредставительной» выборки. При этом выясняется, что в отсутствии связи между лечебным эффектом и дозой полученная «зависимость» наблюдалась бы только в 5 из 1000 экспериментов. Итак, в данном случае исследователям просто не повезло. С меньшей вероятностью им бы «не повезло», если бы они взяли больше испытуемых.

 
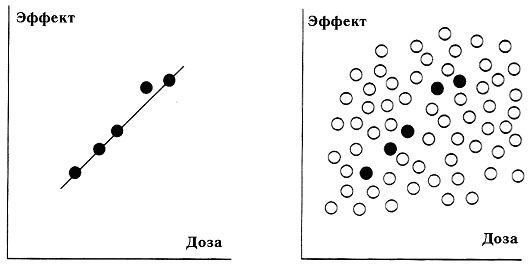
а — на этапе исследования; б — при широком лечебном применении
Рис. 3. Результаты испытания лекарственного препарата

 
     Рассмотрим другой пример. Пусть имеется некая группа из 200 человек, которая по показателю роста имеет распределение, близкое к «идеальному» (рис. 4, а). Три независимых исследователя попытались оценить средний рост М этой группы по выборкам из 10 человек и получили существенно различные результаты М1, М2, М3 (рис. 4, б, в, г, выборки обозначены затемненными кружками на рис. 4, а). При этом, если статистически сравнить первую и вторую выборки по средним значениям, то можно прийти к выводу о статистической значимости их различий и о принадлежности этих выборок к различным генеральным совокупностям, хотя это не так. Здесь налицо ошибка первого рода, вызванная малочисленностью выборок, в процессе извлечения которых сильно проявляется фактор случайности.

Рис. 4. Распределение роста в выборке из 200 человек (а) и в трех случайных подвыборках по 10 человек (б, в, г)