г Кулаичев А.П. Статистическое исследование диагностической информативности показателей вариабельности сердечного ритма.
Функциональная диагностика, №1, 2012, С.56-64
Statistical Investigation of Diagnostic Informativeness
of Heart Rate Variability Indexes
A.P. Kulaichev
При анализе вариабельности сердечного ритма (ВСР) в качестве числовых оценок преимущественно используются показатели вариационной пульсометрии (ВП), спектрального анализа (СА) кардиоинтервалов (КИ) и корреляционной ритмографии (КР). Существующее здесь множество разнородных оценок [1, 2, 3, 7] на первый взгляд представляется плохо упорядоченным и структурированным, а в значительной степени — и избыточным. Поэтому интересна задача их взаимного и комплексного статистического сравнения с использованием, в частности, метода факторного анализа [8, с. 315-349, 421-456].
Исходные данные и их селекция
В качестве исходного материала мы использовали базу кардиозаписей спортсменов
высшей квалификации (ммк, мс, кмс) нескольких видов спорта: футбол, баскетбол,
хоккей, шорт-трек, дзюдо, собранную в 2000—2003 гг. профессором РГУФК В.К.
Зайцевым [4]. Эта база включает 754 двухминутные записи, выполненные с
временным разрешением 1 мс в состоянии релаксации (сидя в удобной позе,
глаза закрыты). Такой характер исходных данных позволяет надеяться на опосредованное
отражение в нем некого «высоко энергозатратного и энергоемкого» норматива
сердечной деятельности.
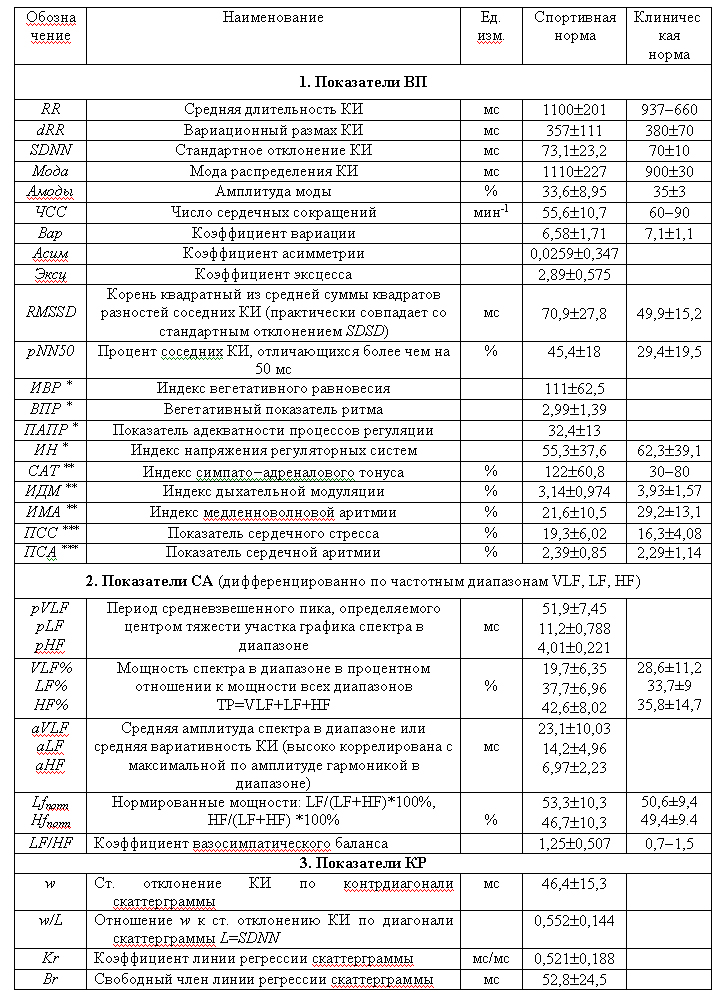
По каждой записи были вычислены 36 наиболее употребительных в практике
показателей ВП, СА и КР (табл. 1). Тем самым была получена матрица размером
36 столбцов (показатели, в факторном анализе называемые переменные) на
754 строк (измерения, в факторном анализе называемые объекты), которая
и явилась материалом для статистического анализа.
Задача осложнялась утратой детальной информации о тех условиях, в которых
осуществлялась регистрация. Это могли быть записи, выполненные в соревновательный,
тренировочный, межсезонный или восстановительный периоды, в разное время
суток, до или сразу после интенсивных нагрузок, после функциональных проб
и т.п. Кроме того, в исходных данных присутствовали артефакты, связанные
с ошибками распознавания R-зубцов, удлиненными КИ и экстрасистолическими
сокращениями. Для корректного же выделения главных факторов необходима
тщательная очистка исходных данных от различного типа выбросов [8, с. 319,
465], определенных влияние вышеперечисленных посторонних факторов. Поэтому
для обеспечения однородности исходных данных была разработана многоступенчатая
схема их очистки, а именно: значения показателей пересчитывались в шкалу
стандартных отклонений от среднего, и из матрицы удалялись строки (выбросы),
отвечающих следующему критерию: наличие у четырех и более показателей (т.е.
у более чем 11% из 36 переменных) значений, превосходящих три стандартных
отклонения (комплексный выброс). Такая процедура последовательно повторялась
до тех пор, пока сформулированное условие удаления не перестало выполняться.
Конкретная формулировка критерия комплексного выброса зависит от вероятности
появления таких выбросов, которая в свою очередь зависит от числа показателей
и числа записей. Для наших данных несложный расчет [8, с. 419] показывает,
что вероятность появления даже одного комплексного выброса в выборке из
754 исходных записей составляет менее 0,6%, и этот процент уменьшается
с последовательным уменьшением объема выборки.
В результате в матрице осталось 378 строк (50% от исходного объема).
О качестве результата очистки данных можно судить по тому, что облако рассеяния
объектов в проекции на главные факторные плоскости является однородно и
симметрично распределенным, не структурировано на отдельные группировки
и не окутано размытым, «рыхлым» гало резких выбросов.
Границы нормы
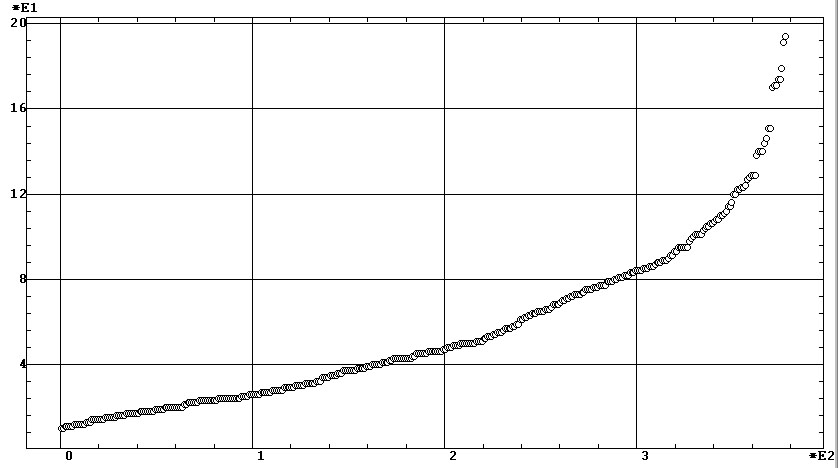
а) |
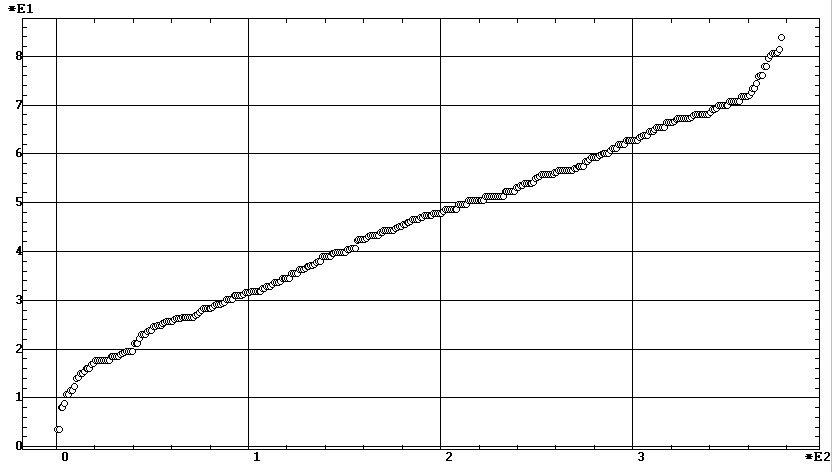
|
После этого в качестве границ нормы можно принять два стандартных отклонения,
покрывающих 95,72% нормально распределенной генеральной совокупности.
Для очищенных по этой методике данных были вычислены средние значения показателей
и их стандартные отклонения (табл.1), где «клинические» нормативы преимущественно
заимствованы из [1]. Как видно из табл. 1, значения клинической и спортивной
норм для большинства показателей достаточно близки, что еще раз свидетельствует
об эффективности проведенной очистки исходных данных. Отдельные различия
могут быть следствием более оптимального в смысле энергоотдачи и энергоемкости
состояния организма спортсменов.
Табл. 1. Показатели вариабельности сердечного ритма
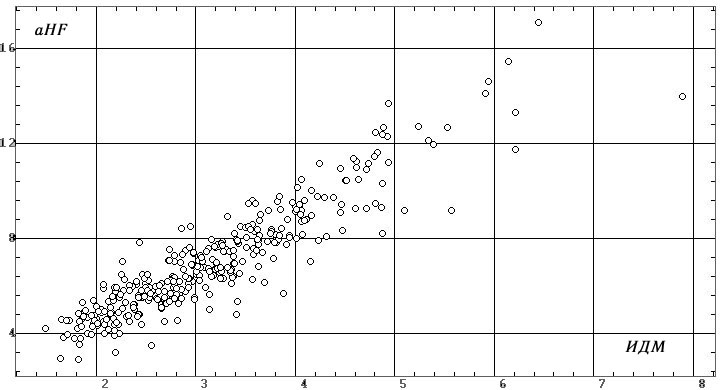
Зависимые и коррелированные переменные
а) |
б) |
Совместный анализ показателей
а) |
б) |
в) |
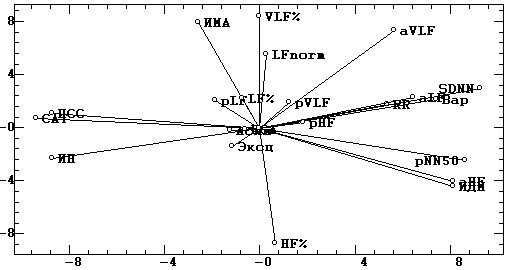
а) |
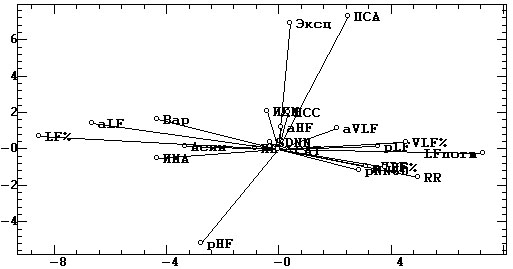
б) |
Из визуального анализа этих проекций можно сделать следующие выводы.
1. На горизонтальную ось фактора 1 (рис. 4, а) проектируются с разными
знаками две группы показателей: САТ, ПСС, ИН и SDNN, pNN50, Вар, RR, LF%,
ИДМ, HF%. Тем самым этот фактор, в основном, определяется теми показателями,
которые характеризуют соотношение напряженного и уравновешенного состояния
организма.
2. На вертикальную ось фактора 2 проектируются переменные, характеризующие
соотношение медленноволновой (ИМА, VLF%, LFnorm) и высокочастотной (HF%)
составляющих в сердечном ритме.
3. На третий фактор (горизонтальная ось рис. 4, б) проецируются преимущественно
показатели СА. При этом разные показатели диапазона LF вступают как антагонисты,
что может свидетельствовать или о неоднозначности данного диапазона, или
о искажающем влиянии показателей ВП на факторную структуру показателей
СА.
4. На четвертый, малозначимый фактор проецируются Эксц и ПСА.
5. Имеет смысл отметить также «факторную близость» индекса ИМА к LF% и
LFnorm (рис. 4, а), а также к LF% и аLF (рис. 4, б), а индекса ИДМ — к
аHF (рис. 4, а). Тем самым эти индексы ВП действительно отражают именно
то, для чего они и задумывались [5] — медленноволновые и дыхательные компоненты
сердечной деятельности.
Первые четыре вывода позволяют высказать предположение о том, что показатели ВП и СА отражают существенно различные аспекты сердечной деятельности, они демонстрируют факторную несвязанность, ортогональность друг к другу. Это подтверждает и корреляционный анализ: корреляции «мощностных» индексов с большинством показателей ВП не превышают 0,1-0,2. Поэтому на следующем этапе целесообразно произвести раздельный анализ этих двух категорий показателей.
Анализ показателей вариационной пульсометрии
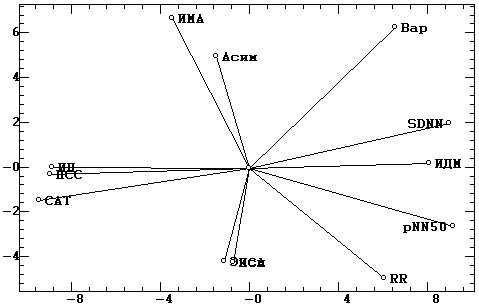
а) |
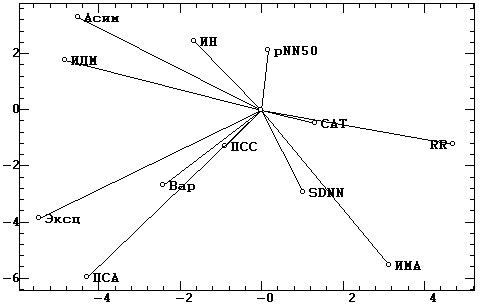
б) |
а) |
б) |
Из визуального анализа этих проекций можно сделать следующие выводы.
1. Первый доминирующий фактор (рис. 5, а), также как и по вышеприведенным
результатам совместного анализа, определяется показателями напряженности
сердечной деятельности САТ, ПСС, ИН и их контрпартнерами SDNN, pNN50, ИДМ.
Тем самым этот фактор, несомненно, является устойчивым и ведущим.
Следует также отметить, что хотя показатели САТ, ПСС, ИН имеют близкое
факторное расположение и связаны частными корреляциями от 0,522 до 0,312,
но рассматривать их как идентичные или близкие нет достаточных оснований.
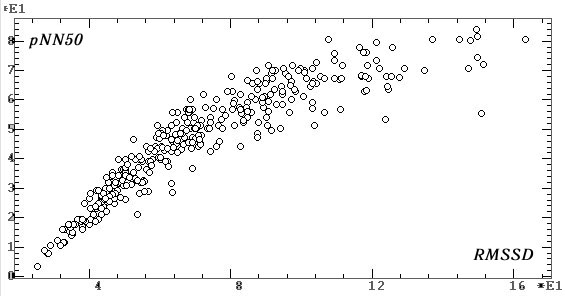
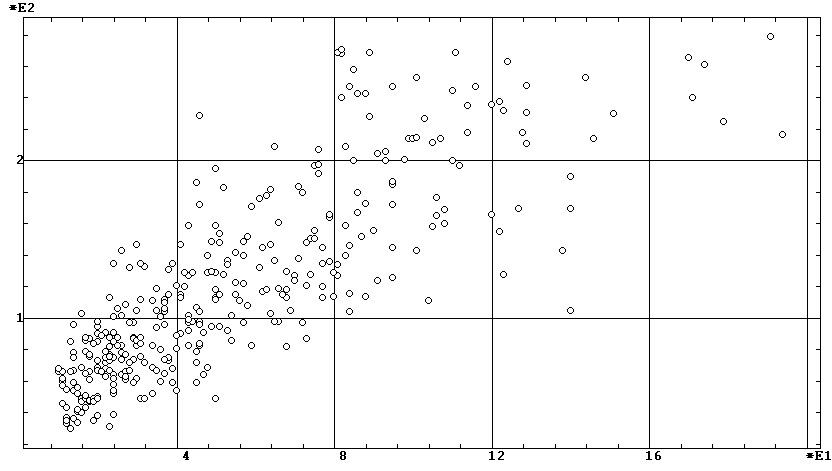
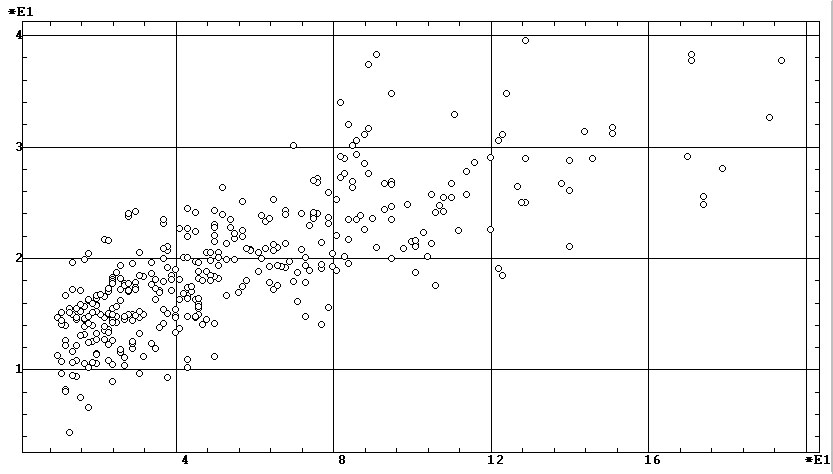
Действительно, их диаграммы рассеяния (рис. 6) достаточно «распылены»,
и на фиксированное значение одного показателя приходится от 25 до 50% диапазона
другого показателя (по сравнению с показателями на рис. 2, а, б). Тем самым
они могут по разному «работать» и иметь разную эффективность при оценке
разных функциональных состояний и функциональных проб.
2. Второй фактор частично определяется двумя антагонистическими парами
показателей (рис. 5, а): Асим, ИМА и Эскц, ПСА. Поэтому его можно обозначить
как характеризующий соотношения стабильности, вариативности, аритмичности
сердечной деятельности.
3. На третий фактор (рис. 5, б) частично проецируются показатели Асим,
Эскц, ИДМ и RR.
4. Четвертый фактор преимущественно определяется ПСА и частично — ИМА и
Эксц. Большинство из этих показателей уже имеют доминирующие проекции в
плоскости первых двух факторов, поэтому здесь самостоятельное их факторное
значение не велико.
Тем самым фактически
здесь мы наблюдаем двухфакторную структуру, где последующие факторы лишь
дифференцируют вторичные различия показателей. Существенное увеличение
значимости первого фактора с 32,3% до 47,6% указывает на то, что его действие
при совместном анализе маскировалось присутствием показателей СА. Это является
дополнительным подтверждением предположения о различной факторной природе
показателей ВП и СА.
Анализ спектральных показателей
а) |
б) |
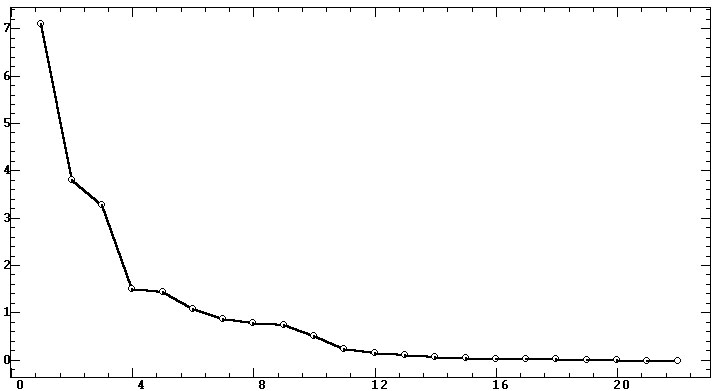
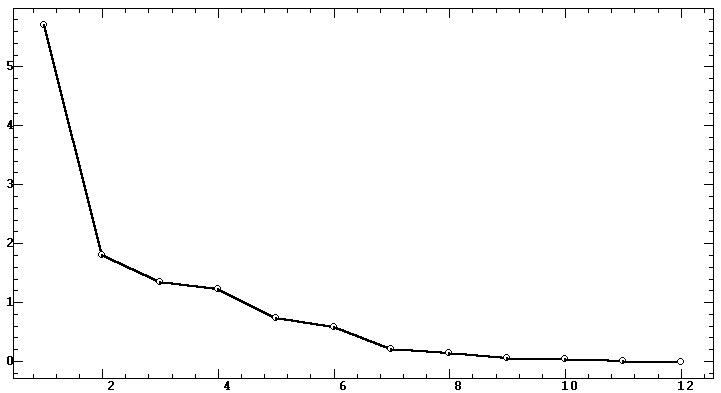
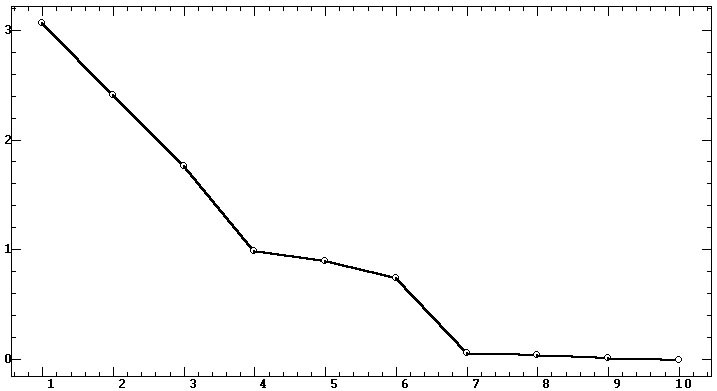
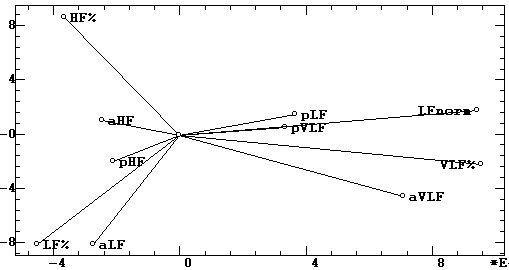
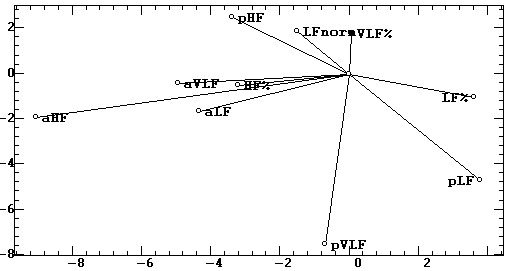
Из визуального анализа этих проекций можно сделать следующие выводы.
1. Такую факторную структуру нельзя признать однозначной или «простой»
[8, с. 327], поскольку выделяется достаточно много (шесть) факторов в пространстве
всего лишь 10 показателей, характеризующих три частотных диапазона. Такая
факторная структура в статистике называется «слабой», и она характерна
для переменных, взаимные значения которых соотносятся подобно случайному
шуму, и их совокупность не несет общей значимой информации. Тем самым показатели
СА существенно разнородны между собой даже в рамках одного частотного диапазона.
2. Принципиальное различие факторных структур показателей ВП и СА окончательно
подтверждает предположение о их факторной несовместности.
3. Факторной устойчивостью обладает только диапазон HF: все его три показателя
проецируются на первый и третий факторы (горизонтальные оси на рис. 7,
а, б). Другие диапазоны не обладают таким свойством: их показатели проецируются
на разные факторные оси, то есть они ортогональны друг к другу, не связаны
между собой. Тем самым значимость диапазонов LF и VLF для функциональной
диагностики вызывает большие сомнения. По-видимому, они не отражают устойчивые
и значимые аспекты сердечной деятельности. Отметим, что выводы 2, 3 согласуются
с результатами ряда исследований, например, [11].
4. Рассмотренная ситуация со слабой факторной структурой нисколько не улучшается,
даже если ограничиться показателями только одного частотного диапазона.
Так в диапазоне HF, наиболее обоснованном в плане физиологической интерпретации,
среди 7 показателей выделяются 4 главных фактора покрывающих 99.1% дисперсии
объектов с ее соответственным распределением в 39.78, 25.87, 21.85, 11.59%.
Поэтому, не следует рекомендовать
использование оценок мощности спектра, которые плохо согласуются друг с
другом, поскольку прямо зависят от размеров частотных диапазонов, которые
в свою очередь различаются в 2—6 раз. В этом отношении предпочтительнее
использование средних амплитуд спектра, которые в свою очередь не плохо
коррелируют с рядом показателей ВП в диапазоне значений от 0,4 до 0,7.
Для функциональной диагностики
вместо неустойчивых показателей СА можно рекомендовать использование вышеотмеченных
вариационных показателей ИДМ и ИМА (вывод 5 из раздела совместного анализа).
Погрешности
спектра кардиоинтервалов. Остановимся на некоторых инструментальных
погрешностях спектрального анализа (подробнее см. в [7, С. 185-191, 199-203])
применительно к последовательности кардиоинтервалов, обычно визуализируемой
интервалограммой (см. также [3]). Во первых, мощности в частотных диапазонах
существенно зависят от «реального» разрешения по частоте, которое в свою
очередь зависит, по крайней мере, от трех факторов: от длины записи ЭКГ,
от величин КИ и от выбранного шага перенормировки последовательности КИ
для приведения ее к равномерному временному шагу. Это уже само по себе
накладывает ограничения на сравнимость различных спектров даже в нормализованном
виде.
Теперь попробуем упростить
эту многоплановую ситуацию и будем рассматривать типичную 2-минутную интервалограмму
со средней длительностью КИ, равной 1 с, как идеальный временной ряд, включающий
120 измерений, выполненных с фиксированным шагом 1 с. Тогда в полосе от
0 до 1 Гц мы будем иметь 60 спектральных линий с шагом 0,017 Гц, которые
распределяются по частотным диапазонам от 0 до 0,4 Гц следующим образом:
HF — 15 спектральных линий, LF — 6 и VLF — 3. Понятно, что говорить здесь
о хорошем спектральном разрешении в диапазонах LF и VLF достаточно проблематично.
В такой ситуации утечка мощности от высокоамплитудных пиков и боковые пики
вследствие амплитудной модуляции ритмики будут простираться далеко в соседние
диапазоны, внося значительные и неконтролируемые искажения. При более длительных
интервалах наблюдения разрешение по частоте улучшается, но начинают сказываться
эффекты смены ритмики вследствие привыкания, утомления и нестабильности
функционального состояния, в связи с чем искажения от медленной амплитудной
модуляции могут существенно возрасти, а амплитуды спектральных пиков понизиться.
Во вторых, при записи
ЭКГ не нормируется главный действующий фактор — дыхательный ритм, который
может иметь разную частоту и глубину (частота дыхания регламентируется
только в пробах глубокого дыхания и гипервентиляции). А о сравнимости спектров
в диапазонах HF и LF можно было бы вести речь только тогда, когда пробы
выполняются с фиксированным периодом и амплитудой дыхания. Для учета и
контроля влияния дыхательного ритма следовало бы запись ЭКГ дополнять регистрацией
грудного и брюшного или носового дыхания, вычленяя из интервалограммы или
корректируя корреляционные влияния.
И, наконец, само разбиение
спектра КИ на существующие диапазоны достаточно условно и статистически
не обосновано. Для такого обоснования следовало бы на представительном
экспериментальном материале опробовать различные разбиения и выбрать наиболее
значимое и устойчивое в плане факторной интерпретации.
Отметим, что намного
ранее кардиологии методы спектрального анализа начали применяться в электроэнцефалографии,
и используемое там традиционное разбиение на частотные диапазоны более
глубоко физиологически аргументировано и напрямую связано с различными
функциональными состояниями. Однако и в этой области применение методов
спектрального анализа наталкивается на ряд принципиальных трудностей [9].
![]()