CONAN-m

КРИТИКА ВЕЙВЛЕТ АНАЛИЗА ЭЭГ
г Кулаичев А.П., 2016
ссылки на публикацию: Актуальные проблемы гуманитарных и естественных наук. 12-1: 47-57. 2016.

       Аннотация: Рассмотрены плохо освещенные в литературе свойства вейвлет преобразования и связанная с этим обширная мифология. Предложен простой алгоритм вейвлет преобразования, обеспечивающий заданную полосу пропускания при любой частоте вейвлета. Дан анализ основных искажений результатов, не желательных в исследованиях ЭЭГ, в числе которых: 1) вейвлет преобразование приводит к результирующим усредненным погреш-ностям, доходящим до 64% от средней амплитуды сигнала; 2) результаты использования вейвлетов различного масштаба и частоты плохо сопоставимы между собой из-за некон-тролируемого и нелинейного изменения частотной полосы и эффекта перекрытия полос. Для данной научной области показаны преимущества Фурье-фильтрации перед вейвлет преобразованием.
     Ключевые слова: ЭЭГ, вейвлет преобразование, Фурье-фильтрация, спектральный анализ, классические фильтры.
    Key words: EEG, wavelet transform, Fourier filtering, spectral analysis, classical filters.

ВВЕДЕНИЕ

Как известно, большинство методов математического анализа ЭЭГ было заимствовано из технических и физических приложений теории анализа сигналов, и эти заимствования осуществлялись внешними или приглашенными техническими специалистами (исторический обзор в [8]). При этом часто не учитывались фундаментальные особенности ЭЭГ: 1) нестационарность; 2) негармонический характер источников; 3) наличие амплитудной модуляции. В результате этого были перенесены некоторые неадекватные данной области исследования методы [8, 10].
В частности, с середины 90-х годов в зарубежных публикациях появляются исследования ЭЭГ с инновационным использованием вейвлет преобразования [17] как альтернативы классическому спектральному анализу. Со значительной временной задержкой этот метод начинает появляться и в отечественных работах [5].
Математическая основа вейвлет анализа достаточно сложна для неспециалистов, в частности, для физиологов, и им приходится в этих вопросах всецело полагаться на мнения и пояснения привлекаемых технических специалистов. Сами же эти специалисты используют для анализа программные средства MathLab, поскольку в ЭЭГ-анализаторах такие средства до сих пор отсутствуют. Это еще дальше удаляет понимание используемых процедур и получаемых результатов от внимания физиологов. С другой стороны, вейвлет анализ исходно начал применяться в области сжатия информации, преимущественно видеоизображений, аудио- и сейсмозаписей, что очевидно далеко отстоит от задач исследования ЭЭГ. Отсюда полезно, наконец-то, разобраться, какие преимущества, или же какие проблемы и недостатки влечет использование вейвлет анализа в исследованиях ЭЭГ, а также доступно это изложить.

СУЩНОСТЬ И СВОЙСТВА ВЕЙВЛЕТ ПРЕОБРАЗОВАНИЯ

     Определение. Математически вейвлет преобразование (ВП) определяется как свертка анализируемого сигнала с вейвлетом, что выражается замысловатой интегральной формулой. Наглядное и понятное для неспециалистов пояснение операции свертки достаточно трудно найти. Опираясь на иллюстрацию в редкой по дидактичности классической монографии [19] ее можно озвучить так: в ходе свертки каждая амплитуда сигнала в момент t умножается на вейвлет со сдвигом результата на t, и все эти результаты усредняются для каждого t.
     Мифология. Отсюда сразу следует мифологичность кочующей по многим источникам интерпретации ВП как аналога и альтернативы для спектрального анализа методом преобразования Фурье (ПФ). Действительно, ПФ осуществляет разложение дискретизированного во времени сигнала на последовательный ряд гармонических составляющих кратно возрастающего (ортогонального) ряда частот. Тем самым ПФ преобразует сигнал из временной области («оригинал») в частотную область («образ»). В отличие от этого ВП преобразует сигнал из временной области во временную же область, осуществляя искаженную фильтрацию сигнала в некотором диапазоне частот.
     Вейвлеты Морле. По аналогии с ПФ, осуществляющим разложение сигнала на гармонические составляющие, в исследованиях ЭЭГ из множества более 400 вейвлетов используются гармонические вейвлеты Морле (Morlet), которые обычно задаются формулой: Y(t)=Acos(2pft)*w(t),                                           (1) где: t = время; f – частота вейвлета; w(t)=exp(-t²/Fb) – экспоненциальные множители или колоколообразное Гауссово окно (огибающая для косинуса); Fb – масштаб вейвлета, определяющий его ширину по оси t ; A=1/sqrt(pFb)– нормирующий множитель.

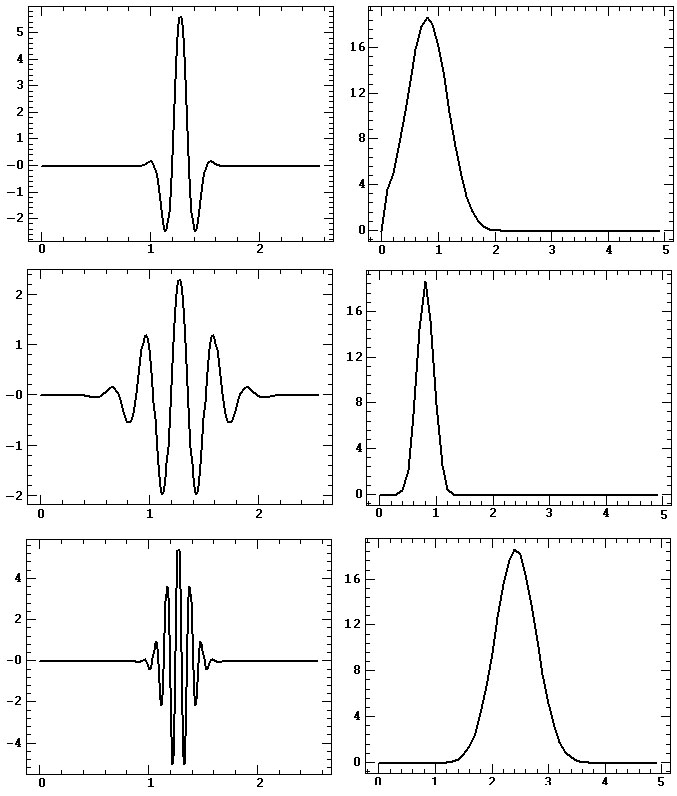
Рис.1. Вейвлеты (слева) различной частоты f, f, 2f и масштаба Fb, 3Fb, Fb (сверху-вниз) и их амплитудные спектры (справа), единицы измерения условные.

     Из иллюстрации рис.1 следует, что при увеличении частоты f спектр вейвлета сдвигается в высокочастотную область, а при увеличении масштаба Fb частотная полоса вейвлета сужается.
     Теорема свертки. Значительно упростить понимание механизма ВП помогает теорема свертки, которая гласит: свертка сигнала с вейвлетом соответствует произведению их Фурье-образов в частотной области. Таким образом, сложная операция свертки в области оригиналов сводится к простому произведению их Фурье-образов в частотной области с последующим ПФ результата, т.е. с применением повторного преобразования Фурье обратно из частотной во временную область, в результате которого и получается свертка сигнала с вейвлетом. При этом амплитудный спектр вейвлета или модуль его Фурье-образа также изменяется согласно Гауссовой огибающей, что упрощает выполнение вейвлет преобразования по следующему простому алгоритму, который для определенности назовем wst-преобразованием (вейвлет-спектральным)
     Wst-преобразование. Анализируемый сигнал характеризуется своей длительностью Т и частотой дискретизации F или временным шагом Dt=1/F, а его спектр имеет разрешение по частоте Df=1/Т . Любой фильтр характеризуется своей полосой пропускания f₁, f₂ или частотами среза, на которых значение его амплитудно-частотная характеристика (АЧХ) составляет 0.5 от максимума на центральной частоте f₀=(f₂–f₁)/2. Определим масштаб спектра вейвлета Fs из условия равенства Гауссовой огибающей половине от единицы на частотах среза, а именно: exp(–(f₀–f₁)²/Fs)=0.5, откуда Fs=–(f₀–f₁)²/ln(0.5). Амплитуды вейвлет спектра А_fj для всего частотного ряда Фурье-образа сигнала f_j=jDf, j=1,...,F/(2Df) вычисляются согласно Гауссовой огибающей: А_fj=exp(–(f₀–f₁)²). Далее эти амплитуды поэлементно умножаются на амплитуды спектра сигнала, в результате чего из спектра наложением колоколообразного вейвлет-окна вырезается заданная частотная полоса. Преобразованием Фурье этого спектра получается свертка сигнала с вейвлетом, определенным его спектром, А_fj, в свою очередь заданным полосой пропускания f₁, f₂ с центральной частотой f₀.
     Подчеркнем, что данный простой и прозрачный алгоритм позволяет выполнять вейвлет преобразование в фиксированной частотной полосе для разных центральных частот f₀, в то время как использование определения вейвлетов во временной области с масштабами Fb приводит к неконтролируемому изменению полос пропускания, гиперболически уширяющихся с уменьшением масштаба (см. ниже).

ПОГРЕШНОСТИ ВЕЙВЛЕТ ПРЕОБРАЗОВАНИЯ

Амплитудные искажения. Таким образом, вейвлет преобразование является своеобразным фильтром, вырезающим из спектра сигнала гармонические составляющие наложением колоколообразного Гауссова окна в диапазоне частот, определенным масштабом и частотой вейвлета. Но при этом возникают амплитудные искажения, для разбора которых произведем сравнение вейвлет преобразования с классической фильтрацией. На рис. 2 приведены АЧХ вейвлета и наиболее распространенного в практике фильтра Баттерворда. Сразу же очевидно наличие у вейвлет-фильтрации двух типов амплитудных искажений по сравнению с фильтром Баттерворда: 1) существенное подавление гармоник в полосе пропускания от средней частоты до частот среза; 2) заметное пропускание гармоник в полосе задержания.
Для каждого испытуемого произведем усреднение по всем электродам значений Аср, получив М(Аср). На рис.2 приведены графики изменения М(Аср) для трех базовых референтов и двух их состояниях (заземленное/незаземленное) в последовательности 10 испытуемых с учетом двух последовательных записей для каждого испытуемого. Как следует из рис.2, приведенные данные подвержены сильной межиндивидуальной вариабельности М(Аср). Кроме того, на рис.2 проявляется наличие внутри-индивидуальной вариабельности (при сопоставлении двух последовательных точек для каждого испытуемого, относящихся к двум последовательно выполненным записям, также как и при сопоставлении рис. 1а,б). И эта вариабельность очевидно несколько ниже по сравнению с межиндивидуальной. Поэтому рассмотрим сначала соотношения между референтными схемами на уровне средних тенденций.

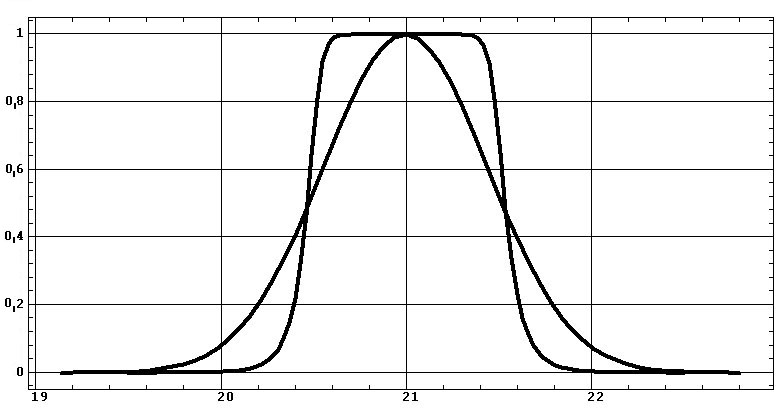
Рис.2. Амплитудно-частотные характеристики фильтра Баттерворда 8-го порядка и вейвлет-фильтра для полосы пропускания 20.5, 21.5 Гц

Классические фильтры. К сожалению, классическим фильтрам (Баттерворда, Чебышева, Бесселя и др.) присущи как амплитудные, так и фазовые искажения, при этом [8]: 1) амплитудные искажения уменьшаются с увеличением порядка фильтра, а фазовые искажения возрастают; 2) при том же порядке фильтра фазовые искажения уменьшаются с уширением полосы пропускания; 3) при однонаправленной фильтрации имеют место также искажения временного сдвига, поэтому при постэкспериментальном анализе используют двунаправленную во времени фильтрацию; 4) имеют место также искажения начального приближения (в том числе и при резкой смене ритмики сигнала), временная протяженность которых увеличивается с увеличением порядка фильтра; при двунаправленной фильтрации эти искажения проявляются на обоих концах сигнала.
Фурье-фильтрация. Поэтому при постэкспериментальном анализе преимущество имеет Фурье-фильтрация [8], впервые предложенная и реализованная в ЭЭГ-анализаторе CONAN-1.5 в 1993 г. Этот метод избавлен от выше отмеченных погрешностей в связи с практически вертикальным характером спада АЧХ на частотах среза, полным пропусканием гармоник в полосе, полным их подавлением вне полосы и сохранением фаз всех гармоник. Иными словами, Фурье-фильтр осуществляет полосовую фильтрацию умножением спектра сигнала на прямоугольное окно. В связи с этим он обеспечивает наиболее адекватный результат, который может использоваться в качестве эталона при дальнейших сравнениях.

ОЦЕНКА АДЕКВАТНОСТИ ВЕЙВЛЕТ ПРЕОБРАЗОВАНИЯ

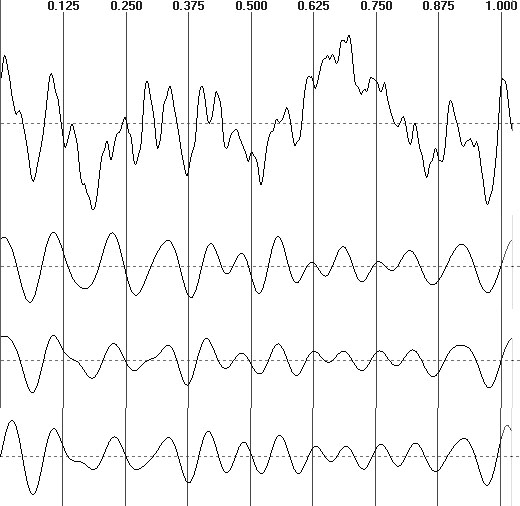
Наглядные примеры. Для последующего анализа будем использовать 1-секундный фрагмент ЭЭГ из эксперимента по исследованию когнитивных вызванных потенциалов на предупредительный и исполнительный стимулы (рис. 3а, отведение О2, частота дискретизации 500 Гц). На рис.3 приведены также результаты Фурье-фильтрации и результаты двух вариантов вейвлет преобразования. Для лучшей демонстрации различий на рис. 3д приведен совместный график этих трех результатов.

а)

б)

в)

г)

в)

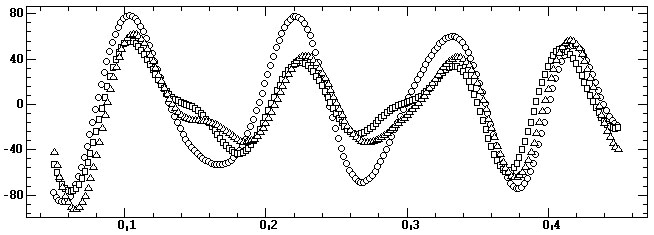
Рис.3. Сравнение результатов, сверху-вниз: а) 1-секундная запись ЭЭГ; б) результат Фурье-фильтрации в диапазоне 8–16 Гц; в) результат вейвлет wst-преобразования; г) результат cwt-преобразования с масштабом 32; д) совместный график результатов на отрезке 0.05–0.45 с: fft – круги, wst – квадраты, cwt – треугольники.

С целью дальнейшей верификации результатов произведем для данного примера ЭЭГ вычисления по следующей программе из справочника MatLab (с некоторыми нашими коррективами):

x=load('signal.txt','-ascii')
cw1 = cwt(x,1:32,'morl','plot');
save cwt1.txt cw11 -ascii
[cw1,sc] = cwt(x,9:32,'morl','scal');
title('Scalogram');ylabel('Scale') в результате чего получена скейлограмма (рис.4), а коэффициенты cwt-преобразования выведены в текстовый файл cwt1.txt для дальнейшего исследования (на рис. 3г изображены эти коэффициенты или амплитуды cwt-отфильтрованного сигнала для масштаба 32).

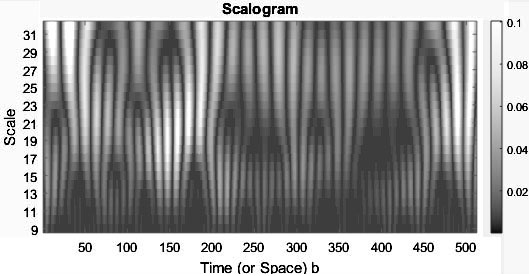
Рис. 4. Скейлограмма или диаграмма абсолютных значений «коэффициентов» вейвлет-преобразования сигнала (черно-белая шкала справа) в зависимости от масштаба вейвлетов (вертикальная ость) и временной развертки сигнала (горизонтальная ось – номер временного отсчета с шагом ?t=0.02 с)

     Терминологический миф. На самом же деле здесь имеет место терминологическая некорректность неизвестного исторического происхождения. Приведем по этому поводу показательное, крайне туманное объяснение из экранного справочника MatLab (безусловно, рассчитанного на очень широкую аудиторию) в разделе Conituous wavelet transform: «Если энергии сигнала и вейвлета равны единице на текущем временном отрезке, то вейвлет коэффициент С может интерпретироваться как коэффициент корреляции. Заметьте, что в общем случае энергия сигнала не равна единице, поэтому коэффициенты не могут быть прямо интерпретируемы как коэффициенты корреляции». Менее туманного и более конкретного разъяснения в различных источниках нам обнаружить не удалось.
     Вместе с тем, эти так называемые “коэффициенты” на самом деле являются амплитудами сигнала, полученного в результате вейвлет-фильтрации исходного сигнала, и обычно измеряются в вольтах. На скейлограммах изображаются абсолютные значения амплитуд таких отфильтрованных сигналов. Поэтому цветовая шкала справа на рис. 4 не имеет к результатам cwt–преобразования никакого отношения, поскольку действительный амплитудный диапазон составляет 0–80 мкВ (рис.3д). Оставим последнее недоразумение на совести системных аналитиков MatLab (на совести которых лежит еще много чего).
     Сравнение двух вейвлет преобразований. Как видно из рис.3д, результаты wst- и cwt-преобразований хорошо совпадают (с учетом приблизительности визуального определения полосы пропускания 8–16 Гц для cwt-преобразования с масштабом 32) и заметно разняться от результата Фурье-фильтрации. Действительно, различия между этими преобразованиями в их абсолютных разностях с Фурье-фильтрацией отсутствуют на уровне значимости р=0.35 по t-критерию и р=0.17 по критерию Вилкоксона (выборочные распределения не нормальны, р<0.0002 по критериям хи-квадрат, омега-квадрат и Колмогорова). Поэтому в дальнейшем мы будем сравнивать результаты Фурье-фильтрации, как эталона, с результатами wst-преобразования, как точно отражающего установленную ширину полосы пропускания.
     Гиперболические искажения. Прежде всего, важно отметить следующее. Как видно из рис.5а, центральная частота и полоса пропускания cwt-фильтра изменяются нелинейно при изменении масштаба вейвлетов, с высокой достоверностью (р<10^-10) эти зависимости являются гиперболическими (рис.5б,в). И если зависимость центральной частоты можно линеаризовать соответствующей интерполяцией с переходом от шкалы масштабов Fb к шкале частот f=f0/(Fb*Dt), то нелинейность полосы пропускания является серьезным и не исправимым недостатком. Подтверждение находим в [17]: «чем больше центральная частота, тем уже временное окно и шире частотная полоса». Из-за этого недостатка результаты cwt-преобразования при различных масштабах становятся несравнимыми.

а) б) в)

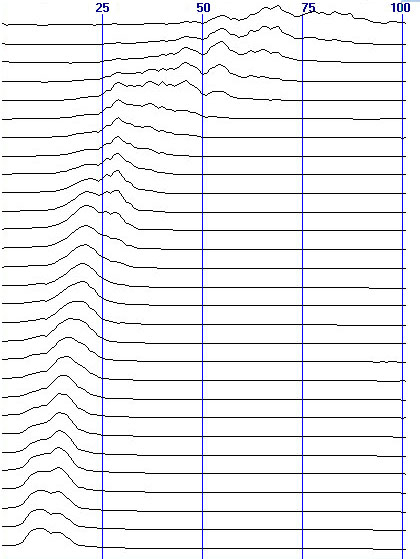
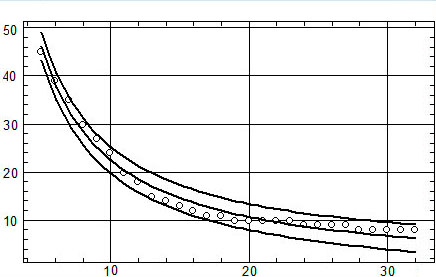
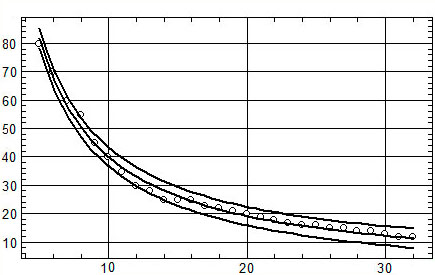
Рис. 5. Результаты вейвлет cwt-преобразования анализируемого сигнала: а) вейвлет-спектры с масштабами 5–32 (сверху-вниз) , горизонтальная ось частот (спектры для масштабов 1–4 не приведены, поскольку представляют широкополосный шум); б) оценки средней частоты спектра [Гц] (круги), выполненные визуально, с регрессией гиперболой Y = -1.36+417/Х; по горизонтальной оси масштаб вейвлета; в) оценки частотной полосы спектра на уровне 0.5 от максимума [Гц] с регрессией гиперболойY = -0.95+236/Х.

Эффект перекрытия полос. Кроме того, в области больших масштабов 32–23, представленных 10-ю нижними спектрами рис.5а (или в верхней трети скейлограммы рис.4), их полосы пропускания имеют взаимное перекрытие от 95% до 50%, то есть они отражают близкую ритмику сигнала, поэтому взаимно не несут принципиально новой амплитудно-частотной информации.
Преобразование к шкале частот. Перерасчет скейлограмм от вейвлет-масштабов к масштабу частот может быть произведен программой из справочника MatLab (с нашими важными коррективами):

Fs = 500;t = 0:1/Fs:1.024-1/Fs;
x=load('сигнал.txt','-ascii')
cfs = cwt(x,9:36,'morl');
pfreq = scal2frq(9:36,'morl',1/Fs);
contour(t,pfreq,abs(cfs));
axis tight;grid on;xlabel('Time');
ylabel('Approximate Frequency (Hz)');
title('CWT with Time vs Frequency');

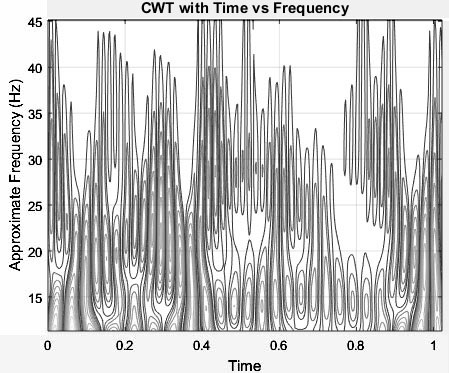
Рис. 6. Скейлограмма рис.4, пересчитанная в шкале частот (вертикальная ось, в области более высоких частот имеет место сплошное белое поле).

     Как видно из рис.6 в сравнении с рис.4 (для лучшего зрительного сопоставления желательно мысленное инвертирование рис.6 относительно горизонтали), при переходе от шкалы масштабов к шкале частот вид скейлограммы существенно меняется, ее низкочастотная половина (с большими вейвлет-масштабами) гиперболически сжимается, а высокочастотная половина гиперболически растягивается.
     Отметим также, что в реальности (рис.5а) вертикальная шкала рис.4 и рис.6 (как и сами изображения) не непрерывная, а дискретная (ступенчатая, несмотря на название conituous wavelet transform, что являет еще один пример мифотворчества). Системные аналитики MatLab и здесь лукавят, применяя тайную сглаживающую интерполяцию.
     Квадратичные искажения. Кроме того, многие авторы используют квадратичное преобразование амплитуд сигналов, как при построении скейлограмм, так и в последующем анализе и выводах [5–7, 11, 12, 14, 17, 18], что резко искажает амплитудные соотношения, гипертрофируя высокие амплитуды и подавляя до полного исчезновения средние и низкие амплитуды. Нетрудно представить себе яростную реакцию врача-энцефалолога или кардиолога, если некий инноватор предложит ему формулировать клинические заключения по энцефалограмме или кардиограмме, амплитуды которой квадратично трансформированы .
     Количественные сравнения. Для количественной оценки различий (рис.3д) эталонной Фурье-фильтрации (ФФ) и вейвлет wst-преобразования (ВП) введем следующие обозначения: Ats – амплитуда сигнала s в момент времени t, |Ats| – абсолютная величина Ats, где индекс s принимает значения: s=ф – результат ФФ, s=в – результат ВП. Нас будут интересовать различия DAtф-в=Atф–Atв и их абсолютные значения |DAtф-в| в сравнении с |DAtф|.
     Сравнение для альфа диапазона (8–13 Гц) статистик (среднее ± стандартное отклонение) по |DAtф-в| = 14.68±9.63 мкВ и |DAtф| = 29.89±20.99 мкВ показывает, что средняя разность между результатами ФФ и ВП превышает 49% от средней абсолютной амплитуды корректно отфильтрованного сигнала, что является несомненно значительным искажением. Аналогичные соотношения имеют место в бета1 диапазоне (14–18 Гц): для |DAtф-в| = 4.46±3.44 мкВ, что составляет 26% от |DAtф| = 17.46±10.11 мкВ, а также в гамма диапазоне (32–48 Гц): для |DAtф-в| = 3.90±2.93 мкВ, что составляет 41% от |DAtф| = 7.12±5.36 мкВ.
     Возьмем для анализа совершенно другой сигнал: стандартная проба «закрытые глаза», интервал 32 с, дискретизация 250 Гц, отведения лобное Fp1 и затылочное O2, стандартные частотные диапазоны альфа и бета1. Результаты приведены в таблице 1.

Таблица 1. Результаты анализа длительного сигнала

Тем самым вейвлет преобразование вносит существенные искажения в амплитудные характеристики и временную динамику сигнала, достигающие 26–64% от средней амплитуды корректно отфильтрованного сигнала.

ОБСУЖДЕНИЕ

     Работы с использованием вейвлет анализа ЭЭГ преимущественно публикуются в научных журналах технической и физической направленности [2, 4, 11–16]. Аналогичная ситуация имеет место и в зарубежных исследованиях (см. литературу из [4, 14]). Это, по-видимому, определено консервативностью физиологической и клинической аудитории к подобным, трудно воспринимаемым математически сложным и запутанным нововведениям. Однако эта ситуация при определенной настойчивости инноваторов может постепенно меняться [3, 5–7, 17, 18].
     Доказательность. Большинство авторов иллюстрируют полученные результаты вейвлет анализа преимущественно различными скейлограммами, скелетонами, временными и частотными графиками [2, 4, 11, 13, 14], иногда дополняемыми гистограммами максимальных значений [12, 15], топографическими картами [17, 18], вычислением корреляций, средних и стандартных отклонений [3, 5–7]. Этот материал обсуждаются преимущественно на основании визуального изучения и словесного сопоставления подобных иллюстраций. Тем самым здесь имеет место самый начальный уровень исследования, лишенный статистических оценок достоверности формулируемых выводов.
     Аргументация. Большинство работ никак не аргументируют использование авторами метода вейвлет анализа или же ограничиваются ссылками на подобные неаргументированные работы предшествующих авторов [2–4, 11, 14] (такие «обоснования» относятся к категории: посмотрите, ведь все так делают). И только в отдельных публикациях к этому добавляются рассуждения довольно отвлеченного характера [16]: «Современные алгоритмы анализа сигнала ЭЭГ извлекают далеко не полную информацию, что приводит к игнорированию ряда важных частотно-временных характеристик исследуемого сигнала и, как следствие, к пренебрежению некоторыми особенностями порождающих их процессов, происходящих в головном мозге», или же [12]: «Для проведения такого анализа (ЭЭГ), требуется применять подходы, отличные от общепринятых, в особенности, если получаемую информацию надо использовать для выявления принципиально новых свойств на основе современных ресурсоемких методик».
     Показательно, что зачинатели внедрения публикаций данной направленности в отечественные физиологические журналы [5, 6] приводят такую аргументацию: «Поскольку Фурье-преобразование для оценки коротких (0.8 с) вызванных ответов оказалось неэффективным, применяли вейвлет-преобразования соответствующих отрезков, используя вейвлет-спектры». Это демонстрирует уровень и глубину обоснования с подачи привлеченных технических специалистов. При ультракритическом отношении это «обоснование» можно перефразировать так: рыбалка в чистой воде не удалась, поэтому стали ловить в мутной. Полезно сравнить, как все это разительно контрастирует с всесторонним и детальным обоснованием эффективности нового метода оценки синхронности ЭЭГ в сопоставлении с его предшественниками [9].
     Мифотворчество. После этого поучительно прикоснуться к сокровенному источнику – к аргументации зачинателей внедрения вейвлетов в мировую энцефалографию [17, 18], цитируем: «Семейство вейвлетов характеризуется постоянным отношением f0/?f, которое должно быть выбрано на практике большим 5 (Grossmann et al., 1989)». Это является примером еще одного мифа. В обозначениях ф-лы 1 это отношение имеет вид:   и, используя гиперболу рис. 5б, легко убедиться, что эта величина не является константой, а возрастает в степени 1/2, как с возрастанием частоты f, так и с уширением полосы пропускания, а по отношению к масштабу вейвлета Fb зависимость обратно пропорциональная.
Здесь же интересна и абсурдная рекомендация, что это отношение должно быть больше 5 или Fb> =123.2/f 2. Так на рис. 5а для вейвлета с масштабом Fb=5 имеем f=70, тогда согласно этой рекомендации должно быть Fb>0.025, т.е. получаем нижний предел для Fb в 200 раз меньше 5, а мы видели, что спектр вейвлет преобразований уже от Fb<5 представляет собой широкополосный низкоамплитудный шум.
     Читаем дальше: «Временное разрешение этого метода возрастает с частотой, а частотное разрешение ухудшается» и отмечаем, что первое является вовсе не следствием использования данного метода, а тем, что высокочастотные составляющие сигнала имеют меньшие периоды колебаний, поэтому их максимумы на скейлограммах располагаются плотнее. А вот то, что частотное разрешение при этом уменьшается (или гиперболически уширяется полоса пропускания) является принципиальным и неисправимым недостатком вейвлетов, задаваемых во временной области.
     В другом источнике [12] читаем: «Скейлограммы можно построить на малых временных отрезках (0.05–0.1 с), что позволяет детально изучить динамику процессов, отражаемых на ЭЭГ». Это тоже относится к категории мифов, поскольку наименьшая величина упомянутого временного отрезка является вовсе не преимуществом данного метода, а определяется: 1) частотой дискретизации сигнала; 2) разрешением по частоте, обратно пропорциональной длительности сигнала. Так на отрезке 0.05 с частотное разрешение составляет 20 Гц, поэтому использование вейвлетов с меньшим частотным шагом невозможно, а это неприемлемо для ЭЭГ, стандартные частотные диапазоны которой в 4 раза более узкие.
     И, наконец, сами формулы вейвлетов Морле в разных источниках различаются своими нормирующими множителями А [11–13, 15, 17]. Это является еще одним признаком произвола, присутствующего в данном направлении и ведущего к несравнимости результатов.
     Таким образом, публикации по вейвлетам в исследованиях ЭЭГ характеризуются формальным и содержательным туманом, систематическим мифотворчеством, произволом, отсутствием статистического обоснования результатов и выводов.
     Альтернатива – метод Фурье-фильтрации. При провозглашаемых цитируемыми авторами задачах можно было бы пойти намного более простым и корректным путем с использованием Фурье-фильтрации, отличающейся наложением в спектральной области не колоколообразного, а прямоугольного окна, не деформирующего амплитудные характеристики исходного сигнала и ширина которого не зависит от частоты, а может быть четко установлена от минимального значения, включающего 2–3 спектральные линии. Это спектральное окно (не путать с оконным преобразованием Фурье) может перемещать по спектру с минимальным интервалом, равным частотному разрешению, тем самым, обеспечивая высоко детализированные скейлограммы и результаты их последующего анализа. А временное разрешение в любом случае определяется средней частотой и соответствующей ей временным интервалом между экстремумами отфильтрованного сигнала.
     Этот метод не подпадает под базисное обвинение из основополагающей отечественной публикации [1]: «В отличие от традиционно применяемого для анализа сигналов преобразования Фурье вейвлет-преобразование обеспечивает двумерную развертку исследуемого одномерного сигнала ... В результате появляется возможность анализировать свойства сигнала одновременно в физическом (время, координата) и частотном пространстве». Неприменимо к этому методу и последующее там же обвинение: «Преобразование Фурье не отличает сигнал, представляющий собой сумму двух синусоид с разными частотами, от сигнала, состоящего из тех же синусоид, включающихся последовательно одна за другой».

ЗАКЛЮЧЕНИЕ

     Мы привели несколько различных криминальных эпизодов некорректности результатов вейвлет преобразования в исследованиях ЭЭГ. Главное состоит в том, что: 1) вейвлет преобразование приводит к результирующим погрешностям, доходящим до 64% от результатов корректного классического спектрального преобразования; 2) результаты использования вейвлетов различного масштаба и частоты плохо сопоставимы между собой из-за неконтролируемого и нелинейного изменения частотной полосы и эффекта перекрытия полос.
     Все это более чем достаточно для вынесения обычного судебного обвинительного заключения. Такие обвинения можно продолжать и продолжать с использованием различных по длительности и характеру записей ЭЭГ. Но это представляется излишним, поскольку вышеизложенная простая процедура реализации вейвлет wst-преобразования с контролируемой шириной полосы пропускания позволяет каждому физиологу с помощью средней руки подручного программиста самостоятельно получать такой обвинительный материал.
     С другой стороны, как известно, при наличии большой серии криминальных эпизодов может быть вынесено и пожизненное судебное обвинение. Мы такой задачи не ставим. Те исследователи, которых это устраивает, имеют право использовать в своих работах средства анализа, дающие искаженные результаты. А те представители научной аудитории, которых это устраивает, имеют право доверять искаженным результатам и выводам таких исследователей. Да и наука в целом тоже имеет право на свободу выбора.

СПИСОК ЛИТЕРАТУРЫ

1. Астафьева Н.М. Вейвлет-анализ: основы теории и примеры применения. УФН. 1996. (166)11: 1145–1170.
2. Божокин С.В. Вейвлет-анализ динамики усвоения и забывания ритмов фотостимуляции для нестационарной электроэнцефалограммы. Журн. техн. физики. 2010. 80(9):16–24.
3. Габова А.В., Гнездицкий В.В., Карабанов А.В., Иллариошкин С.Н., Обухов Ю.В., Морозов А.А., Королев М.С., Шевцова Т.П., Кузнецова Г.Д., Базян А.С. Использование вейвлет-преобразований для анализа электрической активности мозга при болезни Паркинсона. Нервные болезни. 2012. 3:2–6.
4. Грубов В.В., Овчинников А.А., Ситникова Е.Ю., Короновский А.А., Храмов А.Е. Вейвлетный анализ сонных веретен на ЭЭГ и разработка метода их автоматической диагностики. Известия вузов. Приклад. нелин. динамика. 2011. (19) 4:91–108
5. Думенко В.Н., Козлов М.К. Фоновая гамма-активность ЭЭГ и вызванные ответы на лицевые стимулы на модели когнитивной установки. Физиология человека. 2011. 37(4):26–34.
6. Думенко В.Н., Козлов М.К. Динамика мощности гамма-активности ЭЭГ вызванных ответов на лицевую экспрессию в условиях нагрузки на рабочую память. Журн. высш. нервн. деят. 2012. 62(1):20–32.
7. Думенко В.Н., Козлов М.К., Черемушкин Е.А. Мощность вызванных гамма-ответов на лицевую экспрессию при восьмисекундной паузе между целевым и пусковым стимулами. Журн. высш. нервн. деят. 2014. 64(4):401–411.
8. Кулаичев А.П. Компьютерная электрофизиология и функциональная диагностика, 4-е изд., перераб. и доп. ИНФРА-М. 2007. 640 с.
9. Кулаичев А.П. Метод анализа корреляционной синхронности ЭЭГ и его возможности. Журн. высш. нерв. деят. 2011. 61(4): 485*498.
10. Кулаичев А.П. Об информативности когерентного анализа в исследованиях ЭЭГ. Журн. высш. нерв. деят. 2009. 59(6): 757–767.
11. Назимов А.И., Павлов А.Н., Храмов А.Е., Грубов В.В., Ситникова Е.Ю., Храмова Н.Е. Распознавание осцилляторных паттернов на энцефалограмме на основе адаптивного вейвлет-анализа. Вестник ТГУ. 2013. 18(4):1431–1434.
12. Кургалин C.Д., Туровский Я.А., Максимов А.В., Махмуд Н.Н. Вейвлет-анализ энцефалограмм. Информ. технол. в проектир.и производстве. 2010. 1: 89–95.
13. Павлов А.Н., Храмов А.Е., Короновский А.А., Ситникова Е.Ю., Макаров В.А., Овчинников А.А. Вейвлет-анализ в нейродинамике, УФН. 2012. 182(9):905–939.
14. Подкур П. Н., Смоленцев Н.К. Вейвлет-пакетное разложение ЭЭГ на основные частотные ритмы. Вестн. Томск. ун-та. Управл., выч.тех., информатика. 2016. (35)2: 54–61.
15. Сушкова О.С., Королев М.С., Габова А.В., Иллариошин С.Н., Карабанов А.В.,Обухов К.Ю., Обухов Ю.В. Совместный анализ электроэнцефалограмм, электромиограмм и механического тремора при болезни Паркинсона в ранней стадии. Журн. радиоэл. 2014. 5:1–16.
16. Туровский Я.А., Кургалин С.Д., Максимов А.В., Семёнов А.Г. Анализ электроэнцефалограмм на основе исследования изменяющейся во времени структуры локальных максимумов матрицы вейвлет-коэффициентов. Вестник ВГУ. 2012. 2:69–73.
17. Tallon-Baudry C., Bertrand O., Delpuech C., Pernier J. Stimulus specificity of phase-locked and non-phase-locked 40 Hz visual responses in human. J Neurosci. 1996. 16(13):4240–4249.
18. Tallon-Baudry C., Bertrand O., Peronnet F., Pernier J. Induced g-band activity during the delay of a visual short-term memory task in humans. J. Neurosci. 1998. 18(11):4244–4254.
19. Randall R.B. Frequency Analysis, 3rd edition. Bruel & Kjaer, 1987, 344 рp.