REVIEW: The Use of Fluorescence Methods to Monitor Unfolding Transitions in Proteins
M. R. Eftink
Department of Chemistry, University of Mississippi, University, MS 38677, USA; E-mail: chmre@cotton.vislab.olemiss.edu
 M. R. Eftink |
Received September 4, 1997
The advantages and some limitations of the use of fluorescence methods for the quantitative determination of the thermodynamics of protein unfolding transitions (i.e., induced by temperature or chemical denaturant) are discussed. Advantages include the sensitivity, multi-dimensional nature of the data, wide amenable concentration range, high signal-to-noise, rapidity of measurement, and adaptability to a variety of sample compartments. Aside from the need for a probe, some problems associated with the method involve the handling of baselines for the pre- and post-transition regions and the difficulty (shared by most other methods) of discerning whether the transition is two-state or multi-state. KEY WORDS: fluorescence of proteins, protein unfolding, thermodynamics of protein unfolding, tryptophan fluorescence in proteins |
The determination of thermodynamics parameters for the unfolding of globular proteins has been a topic of fundamental interest for many years. Recently such studies have become important for practical reasons, since it is often necessary to characterize the stability of recombinant or "engineered" proteins. Both equilibrium and kinetics studies, along with solution structure studies, are usually needed to try to understand the nature of conformational transitions in proteins, whether these are unfolding reactions or more limited transitions.
The unfolding of a protein can be induced by extreme temperature, pH, high concentrations of chaotropic agents, and high pressure; more limited conformational changes can accompany the binding of specific ligands to a protein. The global unfolding of a protein, from an ordered native state (N, having a narrow range of microstates) to a disordered unfolded state (U, having a wide range of microstates and possibly approaching a random flight coil under certain conditions), can provide key thermodynamic information about the stability of a protein. Chief among these thermodynamic parameters is the free energy change for the N <--> U transition, which is a measure of the stability of the N state with respect to the U state. Depending on the type of perturbation (e.g., temperature, pH, denaturant, pressure) used to induce the unfolding transition, additional thermodynamic parameters are obtained to describe the process.
There are several experimental methods that can be used to track an unfolding transition for the above purpose. One of the most useful and versatile methods is fluorescence spectroscopy. The purpose of this article is to briefly review the advantages and limitations of the use of fluorescence methods to study protein unfolding. Recently our laboratory has published two articles that focus on this general topic [1, 2]; here I will emphasize the more important issues presented in these previous articles, and I will discuss some additional topics.
BASIC CONSIDERATIONS
Consider a two-state transition between a native state, N, and an unfolded state, U. The unfolding equilibrium constant, Kun, partition coefficient, Q, and mole fraction of each state are given as follows.
XN = 1/Q; XU = Kun/Q = 1 - XN, (4)
The value of Kun (or DeltaG0un) will depend on the extent of progress along "the perturbation axis" (T, P, pH, etc.); various functions are generally accepted as describing the dependence of DeltaG0un on these perturbation axes. For thermal and denaturant-induced unfolding, these functions are given in the following equations.
Thermal unfolding:
DeltaG0un = DeltaH00,un + DeltaCp(T - T0) - T[DeltaS00,un + DeltaCpln(T/T0)]. (6b)
In the latter equation, DeltaH0G,un (the value of DeltaH0un at T = TG), DeltaCp, and TG would be fitting parameters, whereas with Eq. (6b) the fitting parameters would be DeltaH00,un, DeltaS00,un, and DeltaCp.
Denaturant-induced unfolding:
Here DeltaG00,un is the free energy change for unfolding at the reference condition in the absence of denaturant (d) and m is a denaturant susceptibility parameter (m = -delta(DeltaG0un)/delta[d]). This equation, referred to as the linear extrapolation model, is the most widely used relationship for describing denaturant-induced unfolding [3].
To track the N <--> U transition, some signal is needed, which must be different for the N and U states for that particular signal to be useful. Frequently the signal is a spectroscopic one, such as circular dichroism, absorbance, or fluorescence. If the signal, Si, of the N and U states are different, then the observed signal, S, will be related to the mole fraction of states. Many spectroscopic signals, including fluorescence intensity, are directly related to the mole fraction of states, as given by the following relationship.
As will be explained below, some fluorescence signals (i.e., steady state fluorescence anisotropy, emission maximum) are not related to the mole fraction of states in the direct manner as described by Eq. (8); more complicated analyses are needed in such cases.
The above two-state model is the simplest model for describing a conformational transition in a protein. An important question regarding protein unfolding is whether the process is two-state or multi-state. That is, whether or not there is one or more intermediates in the unfolding process. The procedure for analyzing fluorescence data in terms of a multi-state model is the same as above, with extension to multiple states and intrinsic signals for each state, but it becomes very difficult to uniquely fit even a three-state model to experimental data. We will give an example of such a fit to data in a later section of this article.
ADVANTAGES OF FLUORESCENCE METHODS
The major advantages of fluorescence methods for studying protein unfolding reactions are the sensitivity of the signal to the microenvironment of the fluorophore, the multi-dimensional nature of fluorescence signals, the wide concentration range over which fluorescence signals can be measured with high signal to noise, the rapid response of the method, and the adaptability of the method to a variety of sample compartments. Additionally, the fluorescence signals of the native and unfolded state also provide some low resolution structural information about these states (at least with respect to the microenvironment of the fluorophores).
The most frequently used fluorophore in studies of protein unfolding is (are) the intrinsic tryptophan residue(s). The indole ring of tryptophan is certainly not one of the more brilliantly fluorescing fluorophores (i.e., indole has a modest molar extinction coefficient and fluorescence quantum yield). Also, its relatively blue absorbance is not well suited for some excitation sources (e.g., xenon lamps or lasers) usually used in fluorescence experiments. However, the fluorescence properties of the indole ring are relatively sensitive to its microenvironment. This latter advantage more than overcomes its shortcomings as a fluorophore for studying protein unfolding. For native proteins, the fluorescence quantum yield of individual tryptophan residues, in single tryptophan containing proteins, is found to be anywhere from about 0.01 to 0.40, a very large range of values [4]. The emission maximum of single tryptophan proteins ranges from 308 nm for the residue in azurin to ~350 nm for fully solvent exposed tryptophan residues [4-6]. By comparison, the fluorescence properties of unfolded proteins (thermal and denaturant-induced) show much less dispersion. There are not many published values for the quantum yield of denatured proteins, but they seem to be approximately 0.1, and the emission maxima of tryptophan residues in unfolded proteins are about 350 nm. Thus there is usually a red shift in the emission of a protein upon unfolding, and the emission quantum yield may either decrease or increase. Since a red shift on unfolding is almost always observed, monitoring the fluorescence intensity at the blue or red edge of the emission envelope will usually result in a measurable signal change.
The wide range of quantum yields and emission maxima of tryptophan residues in proteins must be attributed to differences in the way the excited indole ring interacts with its microenvironment in different proteins. There has been much interest in trying to develop rules for interpreting the fluorescence patterns for tryptophan residues in proteins and relating these data to structural details [7-10]. The most widely accepted interpretation is that bluer emitting tryptophan residues are those with the indole ring surrounded by other apolar amino acid side chains and that interactions between the excited state and polar solvent molecules or other polar functional groups cause redder fluorescence. In cases where the quantum yield of a tryptophan residue in a native protein is very low, this must indicate the presence of some type of intramolecular quenching reaction. Early work by Burstein and coworkers [11, 12] and Ricci and Nesta [13], and more recent work by Barkley and coworkers [14], have documented that the peptide bond and certain amino acid side chains can act as collisional quenchers. Likewise, the emission maximum of a tryptophan residue in a protein is thought to be directly related to the polarity of its microenvironment. An interesting suggestion has recently been made [15] that the emission maximum can also be related to the degree of electrostatic stabilization and destabilization of the excited indole ring (for which there is a greater charge separation, as compared to its electronic ground state) and charged groups in its microenvironment.
Whereas the fluorescence intensity (or quantum yield) is the preferred measurable signal for studying protein unfolding reactions, there are other types of fluorescence signals that can sense a conformational transition, thus increasing the likelihood that a transition will be sensed by some type of fluorescence signal. For example, the exposure a fluorophore to a solute quencher, such as iodide and acrylamide, will probably increase upon unfolding. Such quenchers can then be used to cause a further relative decrease in the fluorescence of the unfolded state. Also, the accessibility of a fluorophore to D2O will probably be greater in the unfolded state; since the quantum yield of indole and most fluorophores is larger in the presence of D2O, this can cause a modulation in the magnitude of the fluorescence signal change relative to H2O as solvent.
Steady-state fluorescence anisotropy data are another type of fluorescence signal that can change upon unfolding of a protein. From the Perrin equation, the anisotropy, r, of a fluorophore is inversely related to (1 + tau/phi), were tau is the fluorescence lifetime of an emitting center and phi is the rotational correlation time that describes the depolarizing process. For native proteins, the value of phi is usually related to the global rotation of the protein, whereas the value of phi for an unfolded protein is usually governed by the segmental motion of the side chain attached to the unfolded polypeptide coil. Thus the phi for an unfolded protein will generally be lower than that of a native protein; consequently, the r for an unfolded protein will usually be lower than that of a native protein (unless the tau values for the two states change in an opposite manner). Since anisotropy measurements require the use of polarizers, which limit the transmission of light, such signals have lower signal-to-noise than simple intensity measurements. However, an advantage of anisotropy measurements is that they are independent of certain experimental variables (e.g., lamp intensity or alignment, or protein concentration, unless the protein undergoes a dissociation of an oligomeric state). In cases where the sample requires hours to reach equilibrium in an unfolding reaction (which is more often the case in chemical denaturation studies), a common practice is to prepare a series of samples at different denaturant concentrations, to allow these to equilibrate for a relatively long period of time (e.g., overnight), and to then measure a fluorescence signal. In such a design, random pipetting errors can lead to variation in protein concentration, which will show up as errors in fluorescence intensity measurements, but not in anisotropy measurements. For the latter reason, anisotropy measurements are popular. However, as discussed extensively elsewhere [1], the quantitative analysis of anisotropy versus denaturant concentration data requires use of an equation different from Eq. (8). Fluorescence anisotropy is related to the mole fraction of N and U states by Eq. (9), where Phi is the fluorescence quantum yield (or relative intensity at the measuring wavelengths) of each state, and ri is the anisotropy of each state.
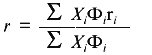 (9)
(9)
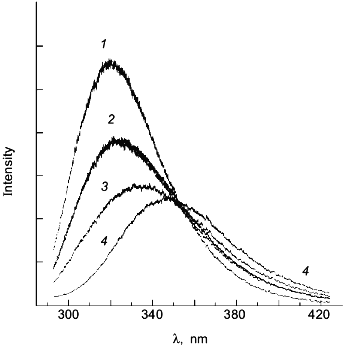
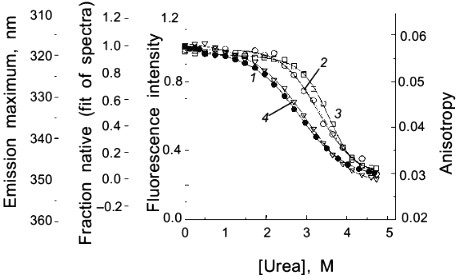
As a second example of how an apparent difference between anisotropy and intensity data can actually be described by the same thermodynamic parameters, consider the data in Figs. 1 and 2 for the urea-induced unfolding of E. coli histidine-containing phosphocarrier protein (HPr). (Actually, the data presented in Fig. 1 are for the F22W mutant of HPr, which has a single tryptophan residue inserted at position 22.) The fluorescence of the native state of this small protein has a maximum at ~320 nm, whereas the unfolded state (in 5 M denaturant) has a maximum at ~348 nm and a lower overall intensity. Figure 1 shows the emission spectra of HPr F22W at a few concentrations of denaturant. Figure 2 shows plots of the fluorescence intensity (curve 1) and anisotropy (curve 2) as a function of the molar concentration of urea. Again, it appears that the protein unfolds at a lower denaturant concentration (mid-point of 2.83 M) for the intensity data as compared to the anisotropy data (apparent mid-point of 3.24 M). However, the dashed lines through the data are a global analysis of Eq. (8) to the intensity data and Eq. (9) to the anisotropy data with the same set of thermodynamic parameters, as indicated in the legend. The reason that the anisotropy data appears to lag behind the intensity data is that, according to Eq. (9), the more dominantly fluorescing N state dominates the anisotropy value. The important point is that an apparent deviation between intensity and anisotropy data may be due to the fact that the quantum yields of the native and unfolded states are not approximately the same and Eq. (9) should be used in such cases.
Fig. 1. The fluorescence spectrum of HPr F22W in the presence of 0, 2.68, 4.13, and 4.75 M urea. Conditions: 20°C, excitation at 290 nm, 4 nm slits, 0.02 M phosphate buffer, pH 7.1. Spectra acquired with a diode array detector. The spectra at 0 and 4.75 M urea were assumed to represent the spectra of the N and U states, respectively. The spectra for the other denaturant concentrations were fitted as a sum of these two basis spectra. For example, the spectrum for 2.68 M denaturant is overlaid with a fitted spectrum with XU = 0.422 ([d] = 0 (1), 2.68 (2), 4.13 (3), 4.5 M (4)).
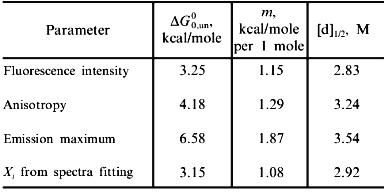
Fig. 2. Use of various fluorescence signals to track the urea-induced unfolding of HPr F22W: 1) fluorescence intensity at 320 nm; 2) anisotropy; 3) emission maximum; 4) mole fraction of N state (from a fitting of the spectra in Fig. 1 to a sum of two component spectra). The signals were individually fitted (solid curves) with Eqs. (1)-(5) and (7) to obtain the following estimates of apparent DeltaG00,un (in units of kcal/mole), m (in units of kcal/mole per 1 mole), and [d]1/2 ([d]1/2 = DeltaG00,un/m, in molarity).
Another fluorescence signal that is often misused in studies of protein unfolding is the emission maximum. The unfolding of a protein almost always results in a red shift in the emission of its tryptophan residues, and this observation can give a qualitative indication of a significant conformational transition. However, the quantitative analysis of emission maximum data to obtain thermodynamic parameters can easily lead to incorrect determinations of these parameters, as illustrated by simulations [1]. The problem again is that the state (N or U) with the larger quantum yield dominates the emission maximum, so that the emission maximum (or the center of gravity of the emission spectrum) will be skewed toward that of the state with the larger quantum yield. The extreme situation is that in which one state is virtually non-fluorescent, in which case the apparent emission maximum will be that of the more fluorescent state under virtually all conditions. To illustrate this point, curve 3 in Fig. 2 is the apparent emission maximum of HPr F22W as a function of denaturant concentration. The apparent transition is shifted to higher denaturant concentration (apparent mid-point of 3.53 M and much higher apparent DeltaG00,un and m values, as compared to that for the intensity data), since the native state has a larger quantum yield than the denatured state of this protein. Rather than using emission maxima or centers of gravity for unfolding studies, a more valid way to analyze emission spectra (besides the approach of simply monitoring the intensity at a single wavelength) is to fit the spectra to basis spectra for the N and U states (e.g., by either using the raw spectra for the extreme conditions as that for N and U or by parameterizing the spectra of these state as gaussian or log normal shapes in wavenumber space) and to then fit the spectra at various denaturant concentrations to ratios of these basis spectra. When this is done for the spectra in Fig. 1 obtained for HPr F22W as a function of urea concentration, we obtain the fraction of U state (curve 4 in Fig. 2), which, when fitted with Eq. (7), gives DeltaG00,un and m values in good agreement with those obtained from the intensity data.A global analysis of intensity and anisotropy data is shown as the dashed curves through these points (difficult to see, since it overlays almost perfectly with the individual fits); the global fit is with DeltaG00,un = 3.32 kcal/mole, m = 1.17 kcal/mole per 1 mole, and [d]1/2 = 2.84 M.
Time-resolved fluorescence measurements can be used to study protein unfolding. Such methods are usually more valuable for characterizing the native and unfolded states than for tracking the transition for the purpose of fitting for thermodynamic parameters. In particular, anisotropy decay measurements can give information about the rotational dynamics of the protein and the side-chain rotational motions of the fluorophore. Although it is possible to do so, usually time-resolved measurements are not made at the same number of points along "the perturbation axes", as is done with steady-state measurements, due to the longer experimental time required in the former. When using time-resolved intensity decay measurements, it is the amplitudes associated with individual fluorescence lifetimes (not the lifetimes themselves) that should track the population of states, at least in an approximate sense. This assumes that intensity decay data are fitted as a sum of exponentials. In some cases, researchers have fitted intensity decay data to a distribution of lifetimes. Since the population of conformational states is most heterogeneous at the mid-point of a transition, it is expected that such an analysis will show the broadest distributions near the mid-point [1]. Fitting data to a distribution model usually does not enable a quantitative analysis of the thermodynamics of the transition. The bottom line is that steady-state intensity measurements are the most useful for the latter purpose.
PROBLEMS ASSOCIATED WITH THE USE OF FLUORESCENCE TO STUDY PROTEIN
CONFORMATIONAL TRANSITIONS
Whereas fluorescence has many advantages for studying protein unfolding, some concerns about the techniques are that there must be a fluorophore that is sensitive to the conformational state of the protein and the fluorescence of the protein may show significant "baseline" trends with increasing perturbation.
Need of a probe. Intrinsic tryptophan residues will usually have the environmental sensitivity to track the unfolding of a protein. There may, of course, be cases where this is not the case, for example, if a tryptophan is on an unstructured region of the protein both in the native and unfolded state. Besides tryptophan, other intrinsic (e.g., tyrosines, riboflavin, pyridoxal phosphate, the pigment in green fluorescent protein) or extrinsic probes can be used. With the latter, it is best to have the probes covalently attached to the protein, or else there will be a coupling between the thermodynamics of probe binding and the unfolding transition. A variety of extrinsic probes are available for labeling side-chain sulfhydryl and amino groups. Probes based on the dansyl group, fluorescein, rhodamine, coumarin, or pyrene all have absorbance and emission that is much redder than does tryptophan, have strong fluorescence signals, and have variable degrees of sensitivity to the conformational state of a protein. When covalently linking a fluorescent reporter group to a protein, it is important to realize that the stability of the protein may be perturbed by the probe. Extrinsic fluorophores tend to be relatively large and charged moieties, compared to amino acid side chains, and thus are to be expected to be at least modestly perturbing to the native state of a protein. Attaching the probe to a surface residue is the preferred strategy. Whether the stability of the protein has been significantly perturbed can be tested by using different fluorescent probes and/or comparing the recovered thermodynamic parameters with those obtained for the unlabeled protein (using an alternate method for tracking the transition).
Baseline problems. When using fluorescence intensity measurements to study protein unfolding, a non-trivial problem is that the "baseline" fluorescence signal of a native or unfolded state of a protein can be intrinsically dependent on the extent of perturbation (i.e., on the concentration of denaturant, temperature, pressure, pH, etc.). In almost all cases these baselines are assumed to be linear functions of the perturbation axis, with baseline slopes being used as floating fitting parameters in the nonlinear least-squares fit of the data (see the example study in Fig. 2, where the pre- and post-transition baseline slopes were floated in the fits).
When using chemical denaturants, urea or guanidine-HCl, the assumption of linear baseline slopes is reasonable, particularly for the fluorescence of the native state. Numerous studies have shown that these chemical denaturants have a small effect on the fluorescence of the native state of a protein (i.e., small baseline slopes). For unfolded states, the baseline slopes are usually larger and positive. Model studies of the effect of urea and guanidine on the fluorescence intensity of tryptophan (or the analog N-acetyltryptophanamide) have shown the fluorescence signals to increase in a slightly nonlinear manner with both urea and guanidine [1, 16]. The departure from linearity is not great for either denaturant and the procedure of assuming linear baselines for both the native an unfolded state seems to be reasonable.
With temperature as a perturbant of protein stability, the assumption of linear baseline slopes is a little more tenuous. From studies of the temperature dependence of the fluorescence of tryptophan and related model compounds, it is known that the fluorescence quantum yield, Phi, of these compounds follow the following nonlinear relationship [17, 18]:
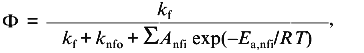 (10)
(10)
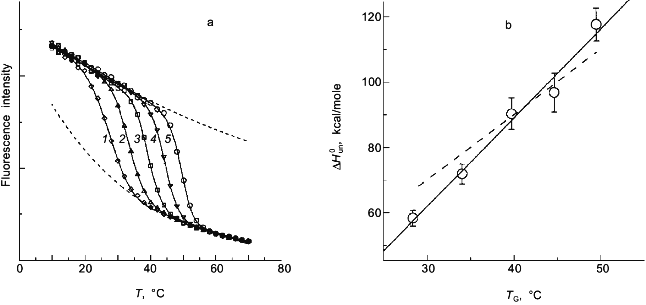
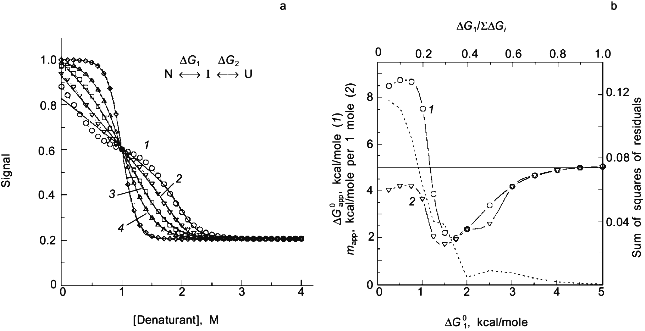
In a previous publication I performed a simulation to show that the recovered thermodynamic parameters for the thermal unfolding of a protein are only modestly influenced by the assumption that of linear baseline regions of the native and unfolded state [1]. This latter simulation, however, did not include the effect of the linear baseline assumption on the recovery of a heat capacity change for the unfolding process. Shown in Fig. 3a is a simulation in which there are non-linear baselines (dashed lines) for both the native and unfolded states and in which there is a heat capacity change, DeltaCp, for the unfolding process. A family of curves was simulated using Eq. (6b) with the same intrinsic DeltaCp, a constant DeltaH00,un, and varying DeltaS00,un (to achieve the different transition mid-points; a 4% random error was included in the simulation). The solid curves are a fit of Eqs. (6a) and (8) to the simulated data with the assumption of linear pre- and post-transition baselines (though they are actually curved in the simulation). In Fig. 3b is plotted the recovered DeltaH0un versus the recovered TG (= DeltaH0un/DeltaS0un); the slope of this plot yields a determination of DeltaCp = 2.7 kcal/mole/deg, which is somewhat higher than the starting value of 2.0 kcal/mole/deg. For comparison, the dashed line is the expected trend of DeltaH0un versus temperature (i.e., a slope of DeltaCp = 2.0 kcal/mole/deg). The discrepancy is exaggerated by the length of the post-transition baseline being fitted (i.e., the curved post-transition baseline is fitted as being linear, which distorts the recovered DeltaH0un and consequently the estimated DeltaCp). The point of the simulation and fits is that non-linear pre- and post-transition baselines can lead to some inaccuracy in the recovery of the thermodynamic parameters when it is assumed that such baselines are linear. The inaccuracy will not be very significant in the recovered values of DeltaH0un, but the inaccuracy will be greatest for the heat capacity change, since it is a higher order thermodynamic parameter.
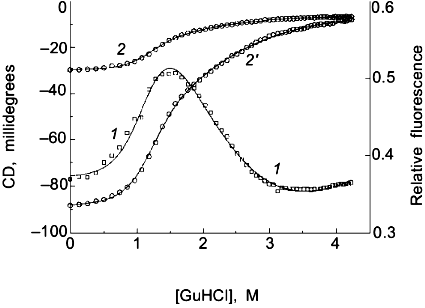
Two-state or multi-state process? Finally I comment that the above discussion has assumed that the unfolding transition is a two-state process. In some cases it will be obvious from the appearance of the data that a mono-phasic (two-state model) fit will not describe the data. For example, shown in Fig. 4 is a plot of fluorescence intensity (right axis) of apomyoglobin versus guanidine-HCl concentration. It is evident that the transition has at least two phases; the fluorescence intensity first increases between 0-1.5 M, reaches a maximum (at the emission wavelength used) and then decreases. A three-state model is able to fit such data.Fig. 3. a) Simulation of fluorescence data for the thermal unfolding of a protein in which the baseline regions for the N and U state is non-linear due to thermal quenching reactions. The activation energy for the N state fluorescence is taken to be 3 kcal/mole and the activation energy for U state fluorescence is 8 kcal/mole (also, assuming kf = knfo = 5.0·107). The simulated thermal transitions were simulated to include these curved baselines using Eq. (6b) with DeltaH00,un = 10.0 kcal/mole (reference temperature, T0 = 0°C), DeltaCp = 2.0 kcal/mole, and with the value of DeltaS00,un varied from 5 (1), 10 (2), 15 (3), 20 (4), and 25 cal/mole/deg (5) to yield the curves from left to right. When fitting the "data", linear baselines were assumed (the normal practice). b) The resulting recovered DeltaH0.
Using a three-state model to fit data is just an extension of the relationships in Eqs. (1)-(7) except that there are more fitting parameters. For example, for a transition N <--> I <--> U, where I is an intermediate state, we can define equilibrium constants, KI/N = [I]/[N] and KU/I = [U]/[I], partition function Q = 1 + KI/N + KI/N·KU/I, and the following mole fractions.Fig. 4. Fluorescence (1) and circular dichroism (2, 2´) data (at 235 (2) and 222 nm (2´)) for the guanidine-HCl-induced unfolding of apomyoglobin. The global analysis (solid curves) yielded DeltaG00,I/N = 2.0 kcal/mole, mI/N = 2.9 kcal/mole per 1 mole, DeltaG00,U/I = 4.1 kcal/mole, and mU/I = 1.7 kcal/mole per 1 mole.
The fluorescence intensity can be related to these thermodynamic expressions via:
where FN, FI, and FU are the "baseline" values for these species (which, as discussed above, may have an intrinsic dependence on the perturbation axis). To fit data along a perturbation axis, the appropriate equation is needed to describe the dependence of the equilibrium constant (KI/N and KU/I) on that axis.
For the guanidine-induced unfolding, such as the data in Fig. 4, there will be thermodynamic fitting parameters for each transition, DeltaG00,I/N, DeltaG00,U/I, mI/N, and mU/I, along with the Fi for each state. For the latter Fi values it will usually be necessary to include a baseline slope value and the value for Fi at some reference state (i.e., the absence of denaturant). Having as many as ten fitting parameters makes it difficult to determine a unique set of fitting parameters. The solid line in Fig. 4 is a three-state fit to the fluorescence intensity data for apomyoglobin. In this nonlinear least-squares fit, we reduced the number of fitting parameters by one by making the simplifying assumption that the baseline slope for the intermediate state is the average of that for the native and unfolded states. (Our experience shows that the slope for an intermediate state is very poorly defined and that such an assumption is needed to achieve a fit.)
The fit for apomyoglobin yields values of for DeltaG0I/N = 2.0 kcal/mole, mI/N = 2.9 kcal/mole per 1 mole, DeltaG0U/I = 4.1 kcal/mole, and mU/I = 1.7 kcal/mole per 1 mole. That is, the N <--> I transition involves a smaller free energy step than does the I <--> U transition. For the guanidine-HCl-induced unfolding of apomyoglobin, we have simultaneously measured changes in the circular dichroism (using a modified dual channel instrument [22]) of the protein to track the transition. The solid curves in Fig. 4 show a global three-state fit of the CD data at two wavelengths, and the fluorescence intensity data.
Actually, the ability to fit the apomyoglobin data to a three-state model is facilitated both by the relatively high population of the intermediate state (which reaches a maximum of XI ~ 0.6 at ~1.5 M guanidine-HCl) and the fact that the fluorescence intensity of the intermediate state is larger than that of either the N or U states. In simulations presented elsewhere [2] we have shown that the ability to detect an I state depends on both the DeltaG0 steps for each transition and the steepness with which the intermediate is formed along the perturbation axis (i.e., a large DeltaHI/N and mI/M favors the formation of the I state along the temperature and denaturant axes, respectively). Also, if the fluorescence intensity of the I state is either larger or smaller than that of either the N or U states, then it will be easier to detect the presence of I, since the biphasic nature of the transition will become more obvious.
We have previously shown simulations of the above two effects and will not repeat them here. Instead I want to stress the point that it will usually be very difficult to determine whether a transition is two-state or multi-state. Since many molecular interpretations of apparent thermodynamic parameters for protein unfolding are based on the assumption that the process is two-state, this point is of paramount importance. Consider the simulations in Fig. 5, in which I have simulated data for a three-state process, N <--> I <--> U, with unfolding being induced by chemical denaturant (assumed to be described by Eq. (7) for each step, with DeltaG01 and m1 for the N <--> I step and DeltaG02 and m2 for the I <--> U step). I have assumed that: 1) the intrinsic fluorescence signal of the intermediate state is midway between that of the N and U states; and 2) the maximum mole fraction of the intermediate increases (from 0 to ~1) due to a change in the ratio of DeltaG01/(DeltaG01 + DeltaG02) (e.g., as might be the case when a set of mutant proteins are compared; note that this simulation assumes that m1 = m2; see [2] for several other simulations of this type). After simulating data, I have then fitted the data to a two-state model, to determine the resulting apparent thermodynamic parameters (for this incorrect model) and to see whether a deviation from a two-state model can be discerned. As shown in Fig. 5, a deviation from the two-state fit can easily be detected when DeltaG01/SigmaDeltaG0i is < 0.3, but, for larger ratios, the data appear to be well fitted by a two-state model. This is true even for cases in which the mole fraction of the intermediate state is a high as 0.7 (corresponding to DeltaG01 = 1.5 kcal/mole, curve 3 in Fig. 5a). Part of the reason for the difficulty in discriminating between a two-state and a three-state process (when, if fact, the latter is valid) is that the signal of the intermediate was assumed to lie between that of the native and unfolded states. Note also for the simulations that the apparent mapp value will be lower than the Sigmami (so-called m-behavior) and that the apparent DeltaG0app can be either larger or much smaller than the SigmaDeltaG0i. The significance of these simulations is to point out that researchers invariably assume an unfolding process to be two-state and then continue to analyze the resulting parameters.
The classical approach for trying to determine whether a process is two-state or multi-state is to compare two or more different types of data that track the unfolding process. We routinely employ this strategy by use of a combined circular dichroism/fluorometer that we have in our laboratory [22]. The data shown in Fig. 4 is such CD and fluorescence data that were simultaneously determined (i.e., all data collected at essentially the same time on a single sample) and analyzed with a three-state model (see the legend for the fitting parameters).Fig. 5. a) Simulated "data" for the denaturant-induced unfolding of a protein for which the unfolding transition is a three-state process described by m1 = m2 = 2.5 kcal/mole per 1 mole and with intrinsic fluorescence signals of FN = 1.0, FI = 0.6, and FU = 0.2 (i.e., the intermediate state has intermediate fluorescence intensity and baseline slopes of zero). The family of curves are simulated with various values of DeltaG01 and DeltaG02 to have a sum of 5.0 kcal/mole and the various ratios indicated in the panel. The simulated data was then fitted with a two-state model to test whether a departure from the two-state fit could be detected. The dark solid lines are the two-state fits and the faint solid lines are a fit to the three-state model. DeltaG1/SigmaDeltaGi is 0.1 (1), 0.2 (2), 0.3 (3), 0.4 (4), 0.8 (5). b) Plot of the recovered "two-state" DeltaG0app and mapp values versus the value of DeltaG01 used in the simulation. The right axis is a plot of the sum of the squares of the residuals (a goodness of fit parameter); we estimate that a deviation from a two-state fit would only be discernable when this value is above 0.04. The horizontal line at 5.0 kcal is equal to SigmaDeltaG0i and Sigmami. The recovered "two-state" DeltaG0app (1) and mapp (2) approach 5.0 kcal when most of the free energy change is associated with the N <--> I step. Note that for most values of DeltaG01, the mapp will be lower than Sigmami and that DeltaG0app can be either smaller or larger than SigmaDeltaG0i.
Thus, fluorescence spectroscopy is one of the most valuable techniques for monitoring the progress of a protein unfolding transition. There are several limitations to the technique which have been highlighted in this manuscript, but the favorable features of fluorescence spectroscopy make it a nearly essential tool for studying protein unfolding. The high signal-to-noise ratio for fluorescence signals and the ability to automate data acquisition for thermal scans and for denaturant and pH titrations leads to data sets of high quality and density, which then are amenable to analyses aimed at determining thermodynamic parameters, including the heat capacity change, for unfolding and in testing the validity of the two-state model.
This work was supported by NSF grant MCB 94-07167. I thank Dr. J. M. Scholtz, Texas A & M University, for a sample of HPr F22W.
REFERENCES
1.Eftink, M. R. (1994) Biophys. J.,
66, 482-501.
2.Eftink, M. R., and Ionescu, R. (1997) Biophys.
Chem., 64, 175-197.
3.Pace, C. N. (1986) Meth. Enzymol.,
131, 266-280.
4.Eftink, M. R. (1991) Meth. Biochem. Anal.,
35, 127-205.
5.Lakowicz, J. R. (1983) Principles of
Fluorescence Spectroscopy, Plenum Press, New York.
6.Beechem, J. M., and Brand, L. (1985) Annu. Rev.
Biochem., 54, 43-71.
7.Burstein, E. A., Vedenkina, N. S., and Ivkova, M.
N. (1973) Photochem. Photobiol., 18, 263-279.
8.Turoverov, K. K., Kuznetzova, I. M., and Zaitsev,
V. M. (1984) Bioorg. Khim., 10, 792-806.
9.Bajzer, Z., and Prendergast, F. (1993) Biophys.
J., 65, 2313-2323.
10.Antonini, P. S., Hillen, W., Ettner, N.,
Hinrichs, W., Fantucci, P., Doglia, S. M., Bousquet, J.-A., and
Chabbert, M. (1997) Biophys. J., 72, 1800-1811.
11.Bushueva, T. L., Busel, E. P., and Burstein, E.
A. (1975) Stud. Biophys., 52, 41-52.
12.Bushueva, T. L., Busel, E. P., Bushuev, V. N.,
and Burstein, E. A. (1974) Stud. Biophys., 44,
129-139.
13.Ricci, R. W., and Nesta, J. M. (1976) J. Phys.
Chem., 80, 974-980.
14.Yu, H.-T., Vela, M. A., Fronczek, F. R.,
McLaughlin, M. L., and Barkley, M. D. (1995) J. Am. Chem. Soc.,
117, 348-357.
15.Burgess, B. K., and Callis, P. R. (1997)
Biophys. J., 72, A346.
16.Schmid, F. X. (1989) in Protein Structure. A
Practical Approach (Creighton, T. E., ed.) IRL Press, Oxford, pp.
251-285.
17.Eisinger, J., and Navon, G. (1969) J. Chem.
Phys., 50, 2069-2077.
18.Robbins, R. J., Fleming, G. R., Beddard, G. S.,
Robinson, G. W., Thistlethwaite, P. J., and Woolfe, G. J. (1980) J.
Amer. Chem. Soc., 102, 6271-6279.
19.Weinryb, I., and Steiner, R. F. (1970)
Biochemsitry, 9, 135-146.
20.Bushueva, T. L., Bushel, E. P., and Burstein, E.
A. (1978) Biochim. Biophys. Acta, 534, 141-152.
21.Szabo, A. G., Stepanik, T. M., Wayner, D. M, and
Young, N. M. (1983) Biophys. J., 41, 233-244.
22.Ramsay, G. D., Ionescu, R., and Eftink, M. R.
(1995) Biophys. J., 69, 701-707.