REVIEW: Protein Folding: Nucleation and Compact Intermediates
O. B. Ptitsyn
Institute of Protein Research, Russian Academy of Sciences, Pushchino, Moscow Region, 142292 Russia; fax: (095) 924-0493; E-mail: ptitsyn@sun.ipr.serpukhov.su
Received August 27, 1997
Experimental and theoretical studies of protein folding have led now to understanding some basic principles of this process. In the simplest case of two-state folding it starts from the formation of the folding nucleus which immediately grows up embracing the whole protein molecule. However, typically folding occurs through a compact intermediate which has some native-like features of its 3D-structure. It is possible that also in these cases the folding nucleus is involved in the transition state between unfolded chain and compact intermediate.
KEY WORDS: protein folding, nucleation--growth mechanism, intermediate states, molten globule, transition states
The overwhelming majority of processes in a living cell are biochemical, i.e., include chemical transformation of biological macromolecules and their complexes. One of the relatively rare exception is the folding of protein chains to their “native” 3D-structures. In fact, Anfinsen discovered [1] that the denatured protein can spontaneously fold into its native 3D-structure in the absence of any help from other cell molecules or organelles. This means that protein folding is an entirely physical process of outstanding biological importance. The possibility to study the mutual insertion of physics and biology on the molecular level have led to the enormous interest in this field which becomes now one of the central points of modern science.
The study of protein folding is now in the stage of its exponential growth. Some ideas and approaches which were very fashionable even a couple of years ago have now become old-fashioned. The common believe in the critical importance of kinetic intermediates in protein folding is now changing by the new truth in “nucleation--growth” two-state folding mechanism. In this short review I shall not follow the chronological order of the studies of protein folding. Instead I shall review two basic hypotheses explaining how protein folds and shall show that each of them are true for some classes of proteins. The problem of synthesis of these hypothesis is waiting for its solution.
Two basic hypotheses on how proteins may fold were formulated in 1972. The hypothesis of Baldwin predicted that proteins should fold according to the nucleation--growth mechanism [2]. According to this hypothesis the rate-limiting step of protein folding is the formation of the folding nucleus after which growth instantly completes the whole molecule. This hypothesis implies the two-state kinetics of protein folding: each protein molecule jumps from the unfolded state directly into the folded state without any intermediates. On the contrary, the hypothesis of the author of this review [3] (see also [4]) postulated that protein folds through intermediate states of increasing levels of order (first secondary structure, then approximate mutual positions of alpha-helices and beta-strands and finally tertiary structure at atomic level).
Baldwin's hypothesis looked consistent with the basic physical principle according to which all macroscopic thermodynamic phase transitions of the first order (i.e., two-state transitions) have nucleation--growth kinetics, like the formation of vapor bubbles upon boiling of water [5]. Since protein folding is a two-state process from the thermodynamic point of view [6], it seems natural that the kinetics of this process should follow the nucleation--growth mechanism. However, relatively soon after the publication of Baldwin's hypothesis it was shown that proteins fold through intermediate states [7, 8], which implies that the rate-limiting step of folding is at the end rather than at the beginning of the folding process. The discovery of the molten globule state of protein molecules [9-11], which shares a number of properties with the main intermediate predicted by the author's hypothesis, has concentrated the efforts of many investigators on the study of the properties and structure of this intermediate (see [12-14] for reviews).
However, in 1991 Jackson and Fersht showed that chymotrypsin inhibitor 2 (CI2, a small protein of 65 residues) has two-state folding kinetics without any observable kinetic intermediates [15]. Afterwards, this behavior was established in a number of other small proteins (see [16, 17] for references). This important discovery has partially shifted the interest from folding intermediates to the two-state folding mechanism, in which the only state which has to be and can be studied is the transition state, i.e., a barrier between folded and unfolded states. Despite the fact that the majority of proteins folds through kinetic intermediates, the discovery of two-state folding was a very important step since it gives the simplest possible model of protein folding.
NUCLEATION--GROWTH MECHANISM
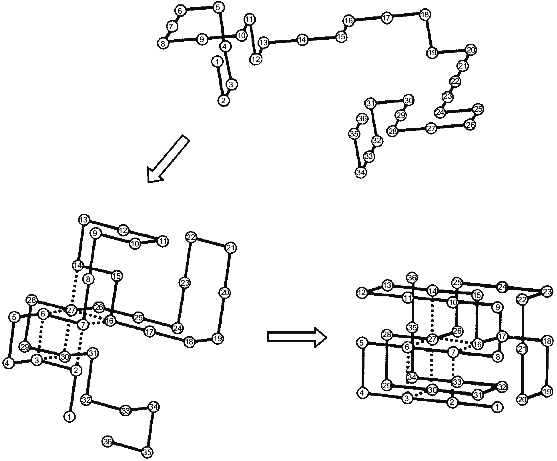
The nucleation--growth mechanism of protein folding was for the first time explicitly considered in the paper of Shakhnovich and his collaborators [18] from computer Monte Carlo simulation of the folding of simple model “chains” on a cubic lattice. The results of their calculations are schematically presented in Fig. 1. The folding starts from an unfolded chain (see the top part of the figure) which fluctuates for a long time without the formation of a substantial part of the native contacts. Then occasionally a chain achieves the state in which a definite set of native contacts is formed (the left bottom part). After the folding reaches this point it comes very fast to the end--to the formation of the “native” structure (the right bottom part). Thus, the rate-limiting step of the folding on these chains is the formation of the initial complex of native contacts (”folding nucleus”) which instantly grows up embracing the whole molecule. It is important to emphasize that a folding nucleus is not identical with the transition state (i.e., with a barrier between unfolded and folded states). In fact, there is a family of transition states while the folding nucleus is the common part of all these states.
The Monte Carlo simulation of protein folding has led to two important results [18]. The first is that protein folding starts with the formation of a definite set of native contacts rather than just of the desired number of any native contacts. The second is that the residues included into the folding nucleus are well scattered along the chain.Fig. 1. Schematic presentation of the folding of a model chain in a cubic lattice according to [18]. Dotted lines mean native residue--residue contacts which form already in the folding nucleus.
Both these results independently have been received also by Fersht and his collaborators from direct experiments using site-specific mutagenesis [19, 20]. This approach has been elaborated [21] for evaluation of transition states which are so unstable and so short-lived that they cannot be studied by any direct method. The idea is to remove the given specific interaction in the native state by site-specific mutagenesis and then to look how much this replacement will change the folding kinetics, i.e., a folding barrier. For instance, replacing a given Ser residue by Ala we can compare the influence of this replacement on the stability of the native state and on the folding barrier. This will permit us to judge whether the native hydrogen bond of Ser's OH-group is present already in the transition state. This approach has been first applied by Fersht's group to the evaluation of a barrier between the intermediate and the native states in three-state folding of barnase [22] and later for the evaluation of a single barrier for two-state folding of chymotrypsin inhibitor 2 (CI2) [19, 20] (see also [16] for review).
The result of these experiments is that CI2 has a folding nucleus consisting mainly from Ala-16 (belonging to a single alpha-helix of this protein), Leu-49, and Ile-57 (belonging to the 4th and 5th strands of beta-sheet) [23]. Ala-16 strongly interacts with Leu-49 and Ile-57 in the native state and these contacts are formed, though in diminished form, already in the transition state between the native and unfolded chain. This suggests that the folding of this protein starts with the formation and simultaneous docking of three key elements of its structure--alpha, beta4, and beta5.
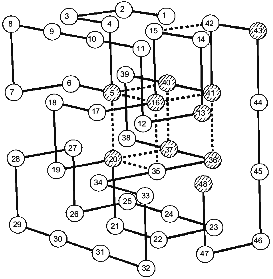
Coming back to Monte Carlo simulations, it is worthwhile to emphasize that they were performed for many sequences stabilizing the “native”, i.e., the energetically most favorable, structure. A very interesting observation was that all sequences stabilizing the same final “native” state have also the same folding nucleus [18]. The possible reason for this behavior is that all these sequences include a common set of conserved residues which ensures the formation of their common nucleus. This idea has been checked and confirmed in our paper with Shakhnovich's group [24]. The results are presented in Fig. 2, which compares the folding nucleus, determined by folding simulation, with the most conserved non-polar residues in about a million different sequences. One can see that the set of the most conserved residues almost coincides with the set of residues entering the folding nucleus. It was also shown that three residues in CI2, which according to site-specific mutagenesis are involved in the folding nucleus (see above), are the most conserved residues according to similar calculations mentioned above [24].
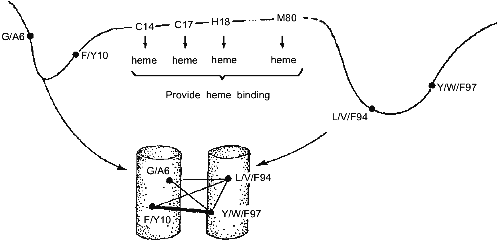
These results have led us to the conclusion that the folding nucleus consists of the most conserved non-functional residues. It opens the possibility to predict the folding nucleus by analysis of large protein families with well diverged sequences but similar 3D-structures. This analysis has been performed recently for the large family of cytochromes c including more than 160 sequences of mitochondria cytochromes c and c1; chloroplast cytochromes c6 and cf, and bacterial cytochromes c2, c551, and c550 [25]. The results of this analysis are presented in Fig. 3, which shows that there are only eight residues which are conserved in all or in the overwhelming majority of these sequences. Four of them (Cys-14, Cys-17, His-18, Met-80) bind the heme by covalent or coordination links and are likely to be conserved for this reason. However, there are another four residues (Gly/Ala-6, Phe/Tyr-10, Leu/Val/Phe-94, and Tyr/Trp/Phe-97) which have structural rather than heme-binding meaning. They form one turn of N-terminal helix and one turn of C-terminal helix and are involved in a set of conserved contacts including the very strong contacts between aromatic residues 94 and 97. This suggests that the common folding nucleus of all considered cytochromes c includes these four residues and that this nucleus is formed by a simultaneous formation and docking of N- and C-terminal helices. It is interesting to note that the complex of these helices has been observed both in kinetic [26] and in equilibrium [27] intermediates of the folding of horse cytochrome c. Moreover, N- and C-terminal helices are tightly packed with each other in this complex [28]. This permits the assumption that the folding nucleus in this protein includes the specific native-like complex of N- and C-terminal helices which then survives in stable or metastable folding intermediates.Fig. 2. Comparison of the folding nucleus in a model chain of 48 residues with the set of the most conserved non-polar residues. The folding nucleus is shown by dotted lines between residues, while the most conserved non-polar residues are hatched (from the data of [19]).
All these results strongly suggest that evolutionary related proteins have two sets of conserved residues--one for the functional center and the other for the folding nucleus. If so, this would mean that the common nucleation of protein folding might be not less important for the given protein family than the function.Fig. 3. Conserved residues in 164 sequences of c-type cytochromes and their role in heme binding and in protein folding. Cylinders in the bottom part mean N- and C-terminal alpha-helices; thin lines, relatively weak residue-residue conserved contacts; and thick lines, strong conserved contacts.
COMPACT INTERMEDIATES IN PROTEIN FOLDING
The two-state folding, which is consistent with the nucleation--growth mechanism, is more or less typical of very small proteins. However, large proteins (starting from, say, 100 residues) typically fold through kinetic intermediate state(s). As early as in the 1970's it was shown that the secondary structure of proteins is restored substantially faster than their rigid tertiary structure [7, 8], which clearly shows the presence of kinetic folding intermediate(s). Similar intermediates with native-like secondary structure but without rigid tertiary structures have been revealed also at equilibrium conditions [29-31].
The first interpretation of these intermediates was that they are unfolded (“expanded”) chains with some secondary structure [31]. However, in 1981 we have shown [9] that these intermediates are compact, which has drastically changed the whole picture. The compact intermediate with the native-like secondary structure but without tertiary structure, without cooperative temperature melting and with fast intramolecular movements was described first in our papers [9-11] and called later the molten globule [32]. These properties resemble the intermediate predicted in 1972-73 (see [3, 4]). Moreover, the native-like mutual positions of alpha-helices predicted in this state [3, 4] have been suggested from deuterium exchange data for a number of proteins [27, 33, 34] and directly revealed in alpha-lactalbumin [35].
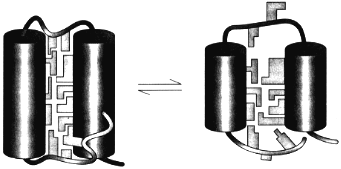
The theory of the molten globule sate [36, 37] and the further study of its properties lead to the physical picture of this state schematically presented in Fig. 4. This figure illustrates that the molten globule preserves some features of the native tertiary fold (i.e., the mutual positions of alpha-helices and/or beta-strands) but has not (or has strongly reduced) tight packing of side chains inside the protein [38]. This makes the molten globule an intermediate between unfolded chain and native protein, like liquid state is an intermediate between gaseous and crystal states of substances.
The important point is that the equilibrium molten globule is the third thermodynamic state of protein molecules separated by all-or-none transition (i.e., by intramolecular analogs of the macroscopic transitions of the first order) from two other states--native and unfolded [11, 39-41]. This implies that a protein molecule can exist in three states--native, molten globule, and unfolded--which can be compared with three usual macroscopic states--crystal, liquid, and gas.Fig. 4. A model of the native (left) and the molten globule (right) states of a protein molecule. According to this model, the molten globule differs from the native state mainly by looser packing of side chains inside a protein molecule and by partial unfolding of loops and ends of a protein chain (adapted from [38]).
The last couple of years have brought important news in our understanding the molten globule state. It was shown that in a number of proteins--cytochromes c [28], equine lysozyme [42], and apo-myoglobin [43]--there is a core of the molten globule state which includes some residues packed probably as tightly as in the native state (see [44] for a recent review). In all studied up-to-date cases this core is in a complex of alpha-helices (like N- and C-terminal helices in cytochrome c or A, G, H helices in apo-myoglobin) which are partly protected from deuterium exchange in the equilibrium molten globule state [27, 33, 34], as well as its kinetic counterpart (see below) [26, 45]. This might explain the existence of two intramolecular analogs of the first order phase transition. It may happen that the transition from the molten globule state to the unfolded state is coupled with the melting of a tertiary structure of a rested core of a molecule, while the transition from the native to the molten globule state is coupled with such melting in other parts of the protein.
Now let us turn to the possible role of the molten globule state in protein folding. It was shown that the molten globule state accumulates upon protein folding [10], that it forms after the formation of a substantial secondary structure [46] and that the kinetic molten globule is a usual intermediate in protein folding [47]. Chain regions partly protected from deuterium exchange in the equilibrium molten globules are in general similar to those on their kinetic counterparts [48], which suggests the structural similarity of these two types of compact intermediates.
The existence of kinetic intermediate(s) means that the folding is not a two-state process. However, the appearance of the second kinetic barrier (between the molten globule-like intermediate and the folded state) is often due to some non-intrinsic (“side”) effects like cis-trans proline isomerization [49], non-native liganding [50], etc. More generally the existence of these intermediates may be connected with the “trapping” of protein chains in some non-global minima of their free energy [51]. Thus, the common reason of the appearing of these barriers are some mistakes in protein folding which can be corrected, for example, by removing of some prolines “essential” for folding [49, 52] or by changing the conditions of the experiment [53].
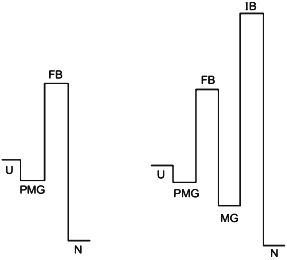
These arguments have led to the conclusion on the existence of barriers of two types [53]: “folding barriers“ (FB) between the unfolded and the intermediate state and the “improving barriers” (IB) between the intermediate and the native states. The important general conclusion from these experiments is that the obligatory steps in folding, like the formation of secondary structure, collapse into a globular structure, side chain packing, etc., are not intrinsically slow and can not be the reason for large barriers which slow down the folding to the usually observed time scale of seconds [54]. The fact that the obligatory steps of folding are very fast permits us to assume that the nucleation--growth mechanism can operate also for three-state folding, where it can refer to the transition from the unfolded state to the molten globule-like intermediate [44, 55]. As to the barrier between this intermediate and the native state, it being even higher can be removed and therefore is not of principle importance for protein folding.
To complete this short review on the role of intermediates in protein folding it is necessary to mention that the formation of the molten globule-like kinetic intermediate is generally preceded by the “burst” stage of protein folding (see [12, 14] for reviews). This stage, which takes place within a few milliseconds consists of the partial formation of secondary structure and partial collapse of protein chains without the formation of the relatively stable features of the native-like 3D-structure [51, 56, 57]. This partially compact and partially structured intermediate has been observed also at equilibrium conditions [58, 59]. It looks more like “squeezed coils” than the real compact intermediates and has been called the “pre-molten globule” state [59].
Recent results on submillisecond folding kinetics (see [60] for review) suggest that the “burst” stage can be much faster than a few milliseconds. The reasonable explanation [60] is that this stage is a barrierless diffusion-controlled process similar to the squeezing of a random polymer coil upon the transition from good to poor solvents [61]. Therefore, the pre-molten globule state may be nothing more than the form in which unfolded chain accumulates before jumping over its folding barrier. On the other hand, it is not necessary to imply the absence of any specific average features in this state. Fluctuations of secondary structure in the unfolded state should be limited by the fact that some parts of a chain are more enriched by the secondary structure-forming residues than others [62, 63]. Moreover, the existence of continuous hydrophobic surfaces of fluctuating alpha- and beta-regions may lead to some specificity of mutual positions of these regions even in this strongly fluctuating but relatively compact state [59]. It would be interesting to study whether some features of the fluctuating native-like 3D-structure can be observed even before the “folding barrier”.
The point of view on protein folding outlined above is summarized in Fig. 5. The figure illustrates two different types of folding--two-state process (left) and three (or multiple)-state process (right). According to our hypothesis both processes start from the formation of the folding nucleus, and the difference between them is that at least in some small proteins this nucleus grows up instantly embracing the whole molecule, while the majority of proteins folds through the compact molten globule-like intermediate. The folding barrier, which each protein molecule has to overcome to fold, is common for both types of folding and is connected with the formation of the folding nucleus.
The improving barrier exists only in proteins which fold through a compact molten globule-like intermediate. This intermediate usually can have crude 3D-structure similar to that of the native protein and even may include a tightly packed native-like core. However, it needs to be “improved” to become the native structure, which is connected with a jump over the improving barrier.Fig. 5. The hypothetical role of the pre-molten globule (PMG) and the molten globule (MG) states in protein folding. According to this scheme, the PMG state is the form in which unfolded state (U) is accumulated before the folding barrier both in the case of two-state folding (left) and of folding through a compact intermediate (right). In the latter case proteins fold through two barriers, but only the first one (folding barrier (FB) between PMG and MG states) plays a principle role in folding. The second one (improving barrier (IB) between MG and the native (N) states) is optional and can be removed by small changes of sequence or environment.
The author thanks A. E. Dujsekina for her valuable help in preparing the manuscript.
REFERENCES
1.Anfinsen, C. B. (1973) Science, 181,
223-230.
2.Tsong, T. Y., Baldwin, R. L., and McPhie, P. (1972)
J. Mol. Biol., 63, 453-469.
3.Ptitsyn, O. B., Lim, V. I., and Finkelstein, A. V.
(1972) in Analysis and Simulation of Biochemical Systems (Hess,
B., and Hemker, H. C., eds.) North Holland, pp. 421-431.
4.Ptitsyn, O. B. (1973) Dokl. Akad. Nauk SSSR,
210, 1213-1215.
5.Lifshitz, E. M., and Pitaevskii, L. P. (1991)
Physical Kinetics, Pergamon, Oxford, U. K.
6.Privalov, P. L. (1979) Adv. Protein Chem.,
33, 167-241.
7.Robson, B., and Pain, R. H. (1976) Biochem.
J., 155, 331-334.
8.Schmid, F. X., and Baldwin, R. L. (1979) J. Mol.
Biol., 135, 199-215.
9.Dolgokh, D. A., Gilmanshin, R. I., Brazhnikov, E.
V., Bychkova, V. E., Semisotnov, G. V., Venyaminov, S. Yu., and
Ptitsyn, O. B. (1981) FEBS Lett., 136, 311-315.
10.Dolgikh, D. A., Kolomiets, A. P., Bolotina, I.
A., and Ptitsyn, O. B. (1984) FEBS Lett., 165, 88-92.
11.Dolgikh, D. A., Abaturov, L. V., Bolotina, I. A.,
Brazhnikov, E. V., Bychkova, V. E., Bushuev, V. N., Gilmanshin, R. I.,
Lebedev, Yu. O., Semisotnov, G. V., Tiktopulo, E. I., and Ptitsyn, O.
B. (1985) Eur. Biophys. J., 13, 109-121.
12.Matthews, C. R. (1993) Annu. Rev.
Biochem., 62, 653-683.
13.Baldwin, R. L. (1993) Curr. Opin. Struct.
Biol., 3, 84-91.
14.Ptitsyn, O. B. (1995) Adv. Protein Chem.,
47, 83-229.
15.Jackson, S. E., and Fersht, A. R. (1991)
Biochemistry, 30, 10428-10435.
16.Fersht, A. R. (1997) Curr. Opinion Struct.
Biol., 7, 3-9.
17.Shakhnovich, E. I. (1997) Curr. Opinion
Struct. Biol., 7, 29-40.
18.Abkevich, V. I., Gutin, A. M., and Shakhnovich,
E. I. (1994) Biochemistry, 33, 10026-10036.
19.Jackson, S. E., ElMasry, N., and Fersht, A.
(1993) Biochemistry, 32, 11270-11278.
20.Itzhaki, L., Oltzen, D., and Fersht, A. R. (1995)
J. Mol. Biol., 254, 260-288.
21.Fersht, A. R., Matouschek, A., and Serrano, L.
(1992) J. Mol. Biol., 224, 771-782.
22.Fersht, A. R. (1993) FEBS Lett.,
325, 5-16.
23.Daggett, V., Li, A., Itzhaki, L. S., Otzen, D.
E., and Fersht, A. R. (1996) J. Mol. Biol., 257,
430-440.
24.Shakhnovich, E., Abkevich, V., and Ptitsyn, O.
(1996) Nature, 379, 96-98.
25.Ptitsyn, O. B. (1997) J. Mol. Biol.,
submitted.
26.Roder, H., Elöve, G. A., and Englander, S.
W. (1988) Nature (London), 335, 700-704.
27.Jeng, M. F., Englander, S. W., Elöve, G. A.,
Wang, A. I., and Roder, H. (1990) Biochemistry, 29,
10433-10437.
28.Marmorino, J. L., and Pielak, C. J. (1995)
Biochemistry, 34, 3140-3143.
29.Wong, K.-P., and Tanford, C. (1973) J. Biol.
Chem., 248, 8518-8523.
30.Robson, B., and Pain, R. H. (1973) in
Conformation of Biological Molecules and Polymers, Vol. 5,
The Jerusalem Symposium on Quantitative Chemistry and Biochemistry
(Bergmann, E. D., and Pullman, B., eds.) Academic Press, London, N.
Y., pp. 161-172.
31.Kuwajima, K. (1977) J. Mol. Biol.,
114, 241-258.
32.Ohgushi, M., and Wada, A. (1983) FEBS
Lett., 164, 21-24.
33.Baum, J., Dobson, C. M., Evans, P. A., and Hanly,
C. (1989) Biochemistry, 28, 7-13.
34.Hughson, F. M., Barrick, D., and Baldwin, R. L.
(1991) Biochemistry, 30, 4113-4118.
35.Peng, Z., and Kim, P. S. (1994)
Biochemistry, 33, 2136-2141.
36.Shakhnovich, E. I., and Finkelstein, A. V. (1982)
Dokl. Akad. Nauk SSSR, 267, 1247-1250.
37.Finkelstein, A. V., and Shakhnovich, E. I. (1989)
Biopolymers, 28, 1667-1680.
38.Ptitsyn, O. B. (1995) Trends Biochem.
Sci., 20, 376-379.
39.Uversky, V. N., Semisotnov, G. V., Pain, R. H.,
and Ptitsyn, O. B. (1992) FEBS Lett., 314, 89-92.
40.Ptitsyn, O. B., and Uversky, V. N. (1994) FEBS
Lett., 341, 15-18.
41.Uversky, O. B., and Ptitsyn, O. B. (1996)
Folding and Design, 1, 117-122.
42.Morozova, L. A., Haynie, D. T., Arico-Muendel,
C., van Dael, H., and Dobson, C. M. (1995) Nature Struct. Biol.,
2, 871-875.
43.Kay, M. S., and Baldwin, R. L. (1996) Nature
Struct. Biol., 3, 439-445.
44.Ptitsyn, O. B. (1996) Nature Struct.
Biol., 3, 488-490.
45.Jennings, P. A., and Wright, P. E. (1993)
Science, 262, 892-896.
46.Semisotnov, G. V., Rodionova, N. A., Kutyshenko,
V. P., Ebert, B., Blank, J., and Ptitsyn, O. B. (1987) FEBS
Lett., 224, 9-13.
47.Ptitsyn, O. B., Pain, R. H., Semisotnov, G. V.,
Zerownik, E., and Razgulyaev, O. I. (1990) FEBS Lett.,
262, 20-24.
48.Baldwin, R. L. (1993) Curr. Opin. Struct.
Biol., 3, 84-91.
49.Schmid, F. X. (1992) in Protein Folding
(Creighton, T. E., ed.) Freeman, New York, pp. 197-241.
50.Elöve, G. A., Bhuyan, A. K., and Roder, H.
(1994) Biochemistry, 33, 6925-6935.
51.Radford, S. E., Dobson, C. M., and Evans, P. A.
(1992) Nature (London), 358, 302-307.
52.Kim, P. S., and Baldwin, R. L. (1990) Annu.
Rev. Biochem., 59, 631-660.
53.Sosnik, T. R., Mayne, L., Hiller, R., and
Englander, S. W. (1994) Nat. Struct. Biol., 1,
149-156.
54.Sosnik, T. R., Mayne, L., and Englander, S. W.
(1996) Proteins: Struct., Funct. Genet., 24, 413-426.
55.Roder, H., and Colon, W. (1997) Current
Opinion Struct. Biol., 7, 15-28.
56.Elöve, G. A., Chaffotte, A. F., Roder, H.,
and Goldberg, M. E. (1992) Biochemistry, 31,
6876-6883.
57.Varley, P., Gronenborn, A. M., Christensen, H.,
Wingfield, P. T., Pain, R. H., and Clore, G. M. (1993) Science,
260, 1110-1113.
58.Uversky, V. N., and Ptitsyn, O. B. (1994)
Biochemistry, 33, 2782-2791.
59.Uversky, V. N., and Ptitsyn, O. B. (1996) J.
Mol. Biol., 215, 215-228.
60.Eaton, W. A., Muunoz, V., Thompson, P. A., Chan,
C.-K., and Hofrichter, J. (1997) Curr. Opinion Struct. Biol.,
7, 10-14.
61.Flory, P. J. (1993) Principles of Polymer
Chemistry, Cornell University Press, Ithaca, N. Y.
62.Ptitsyn, O. B., and Finkelstein, A. V. (1980)
Q. Rev. Biophys., 13, 339-386.
63.Ptitsyn, O. B., and Finkelstein, A. V. (1983)
Biopolymers, 22, 15-25.