QM/MM Model Study on Properties and Structure of Some Antibiotics in Gas Phase: Comparison of Energy and NMR Chemical Shift
M. Monajjemi1*, M. Heshmata2, and H. H. Haeria3
1Science and Research Branch, Islamic Azad University, P.O. Box: 14515-775, Tehran, Iran; E-mail: m_Monajjemi@yahoo.com2Islamshahr Branch, Islamic Azad University Tehran, Iran
3Tehran Shargh Branch (ghyamdasht), Islamic Azad University, Tehran, Iran
* To whom correspondence should be addressed.
Received January 9, 2005; Revision received April 18, 2005
The combination of Quantum Mechanics (QM) and Molecular Mechanics (MM) methods has become an alternative tool for many applications for which pure QM and MM are not suitable. The QM/MM method has been used for different types of problems, for example: structural biology, surface phenomena, and liquid phase. In this paper, we have used these methods for antibiotics and then we compare results. The calculations were done by the full ab initio method (HF/3-21G) and the (HF/STO-3G) and QM/MM (ONIOM) method with HF (3-21G)/AM1/UFF and HF (STO-3G)/AM1/UFF. We found the geometry that has obtained by the QM/MM method to be very accurate, and we can use this rapid method in place of time consuming ab initio methods for large molecules. Comparison of energy values in the QM/MM and QM methods is given. In the present work, we compare chemical shifts and conclude that the QM/MM method is a perturbed full QM method. The work has been done on penicillin, streptomycin, benzyl penicillin, neomycin, kanamycin, gentamicin, and amoxicillin.
KEY WORDS: quantum mechanics, molecular mechanics, ab initio calculations, antibioticsDOI: 10.1134/S0006297906130190
Various computational approaches have strengths and weaknesses. Dramatic progress has been made in the field of computational chemistry in recent years. Molecular mechanics can model very large compounds rapidly. Quantum mechanics is able to compute many properties and model chemical reactions. Of course, QM/MM approaches are different and depend on the methods used for calculations in the QM and MM regions. However there are many other attributes characterizing the various published methods. Chemical systems of interest in computational biology and reaction catalysis are occasionally systems in condensed phase that consist of thousands of participating atoms.
The combination of quantum and molecular mechanics gives very rapid results where only one part of the molecule needs to be modeled quantum mechanically. Today, it is well accepted that the QM method is the ultimate computational tool that can be used successfully in studying the structural aspects of a molecule and a variety of its physical and chemical properties.
Using these calculations energy, bond lengths, bond angles, the strongest bonds, estimation of the active site of a molecule, recognition of reaction mechanism in the body, type of penetration in living cells, and also the presence of antibiotic drug residues in food products of animal origin that has potential health hazard to consumers can be obtained. For example, sulfonamide residues in some species have been a problem for about 10-12 years. Such studies are widespread for biological systems, especially enzymes [1-8].
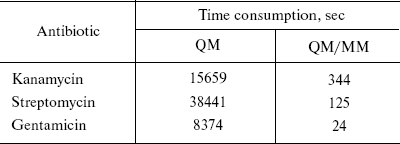
In this study, the QM/MM method is focused on antibiotics [4]. The geometries and NMR shielding tensors have been calculated. The calculated values from both methods (QM and QM/MM) were compared and the results were very close together except in time consumption. For example, optimization times for the largest molecules in this study--kanamycin, streptomycin, and gentamicin--are given in Table 1.
Table 1. Comparison of time consumption for
the three largest antibiotics
METHODS OF INVESTIGATION
Computational details. The GAUSSIAN 98 software package [9] is used to perform Hartree-Fock (HF) and DFT calculations, B3LYP and LSDA, on the antibiotics. The semiempirical calculation is based on the AM1 method and because we use the Gaussian 98 program we must take UFF force field for the molecular mechanic part. Hybrid QM/MM runs were performed as implemented before in the ONIOM method. In many respects, the issues governing implementation of QM/MM computer codes are similar to those associated with the individual QM and MM methods. Most of the coupling terms are readily computed using the machinery present in either the QM or MM packages. However, it is worthwhile to give brief consideration to a couple of implementation issues. Given that the starting point is working QM and MM codes, QM/MM implementations can be considered to fall into three groups [10].
I. Those based on classical modeling packages with a QM code integrated as a force field extension 3.
II. Those based on a QM package incorporating the MM environment as a perturbation.
III. Modular schemes in which a central control program is provided and a choice of both QM and MM methods is left open.
Methodology. On the basis of the ONIOM method, we divided every molecule into three parts (L, M, and H) and then optimized each point. This method cannot optimize some molecules because of having a double bond or aromatic ring in the link part. The link bonds are a critical aspect of the QM/MM method. Usually, we use a dummy atom to complete the QM subsystem. We must note that the link part should always be in the form of Calpha-Cbeta for two subsystems QM/MM. In fact, the relation between the link part and MM or QM subsystems must be through one atom. The QM/MM boundary should not cut across double, triple, or aromatic bonds as [11]. Thus, one link atom can only be bonded to one QM atom. But the reverse situation is allowed; this means that two link atoms are bonded with one QM atom.
The separation of the partial atomic driving force is described as follows. In the ONIOM calculation of the total energy, EREALONIOM (R1... RN; rm+1,rm+2) is approximated by:
EREALONIOM (R1... RN; rm+1,rm+2) = EREALMM (R1...RN) + E MODELQM (r1...rm, rm+1,rm+2) - E MODELMM (r1...rm, rm+1,rm+2),
where the REAL system consists of N atoms at Ri (i = 1, 2...N) and the MODEL system consists of (m+2) atoms at rj (j = 1, 2...m+1, m+2) [12].
RESULTS AND DISCUSSION
According to [12], EREALONIOM (R1... RN; rm+1,rm+2) is the total ONIOM optimized energy for each antibiotic, R1...RN are the coordinates for each atom (1...N) of the molecules, and rm+1,rm+2 are the coordinates for link atoms. EREALMM (R1...RN) is the total MM optimized energy for R1 to RN. EMODELQM (r1...rm, rm+1,rm+2) is the total QM optimized energy for the medium region and link atoms and EMODELMM (r1...rm, rm+1,rm+2) is the total MM optimized energy for the medium region and link atoms [10].
In the present work, we compare the result from pure quantum mechanical (ab initio) calculation of a molecule and the QM/MM results. The calculations were performed using the GAUSSIAN 98 software package [9]. We conclude that these two data groups are in good agreement. Then we can use the QM/MM method for recognizing the active site of antibiotic molecules and mechanism of their reactions in the body. In all test examples the results of QM/MM calculations were compared to the corresponding results of full quantum chemical study. The optimized geometries are summarized in Table 2.
Table 2. Geometric data
comparisona
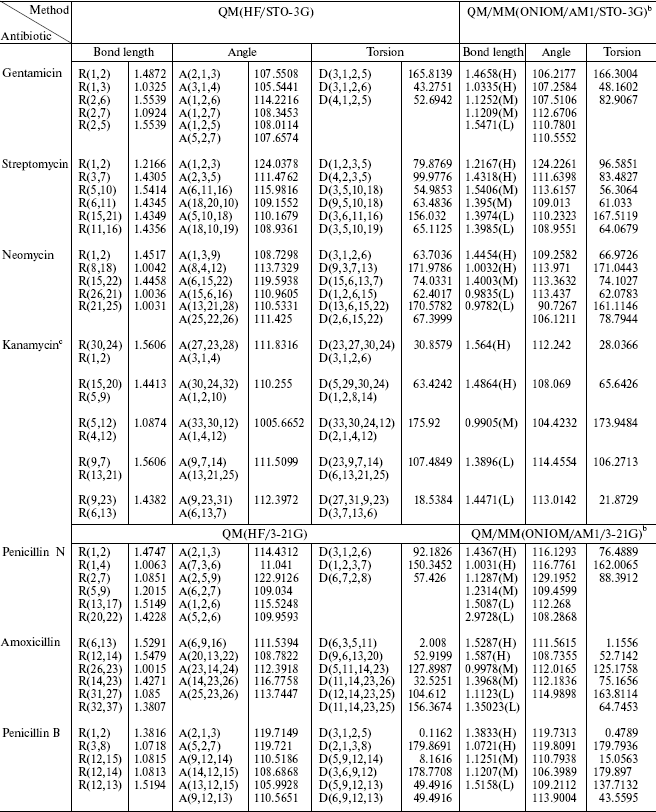
aBond length in Angstroms and angles in degrees.
bH, M, and L are related to the level of calculation.
cAfter optimization, the atom number is different in each method, so we wrote the equal positions. The upper is the nomenclature in QM and the lower in QM/MM.
In ab initio quantum chemistry, analytical derivative theories have made possible the calculations of many important molecular properties. It should be pointed out that a direct comparison of the QM/MM predictions to the experimental data available for the same molecular system is complicated by the fact that the empirical parameterization contained in the MM force fields is partly responsible either for excellent agreement (may be due to successful cancellation of errors) or serious disagreement between two sets of values. In the ONIOM method that we use in this work, particle exchanges between high-level and 4 low-level subsystems do not disturb the statistical ensemble. NMR shielding tensors (ppm) have been computed with the continuous set of the gauge independent atomic orbital (GIAO) method [13-16]. The delta_values for isotropy and anisotropy are shown in Figs. 1-4.
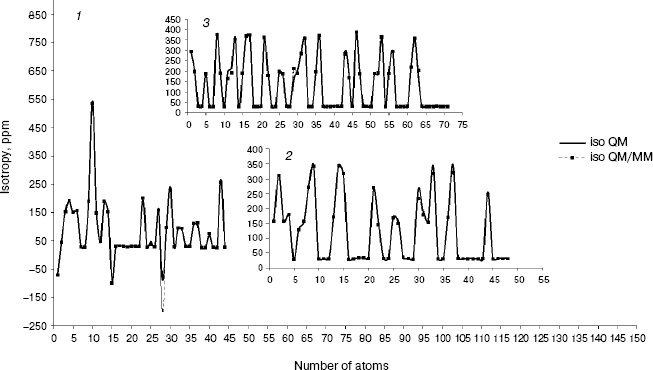
Fig. 1. Calculated NMR isotropy by QM and QM/MM methods for amoxicillin (1), neomycin (2), and gentamicin (3).
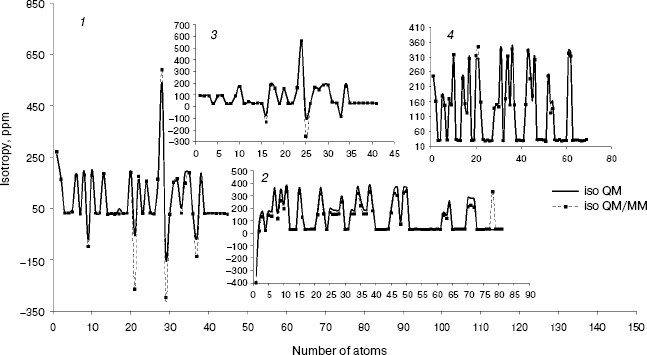
Fig. 2. Calculated NMR isotropy by QM and QM/MM methods for penicillin N (1), streptomycin (2), benzyl-penicillin (3), and kanamycin (4).
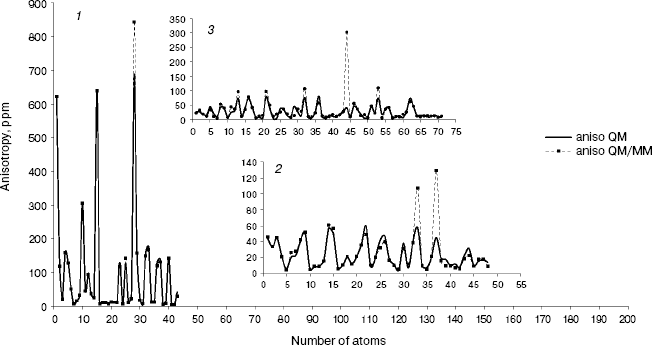
Fig. 3. Calculated NMR anisotropy by QM and QM/MM methods for amoxicillin (1), neomycin (2), and gentamicin (3).
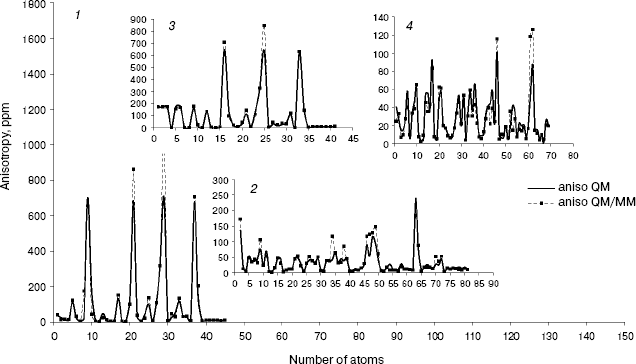
As we see in NMR isotropy and anisotropy for all of the molecules (Table 3), in the high region of calculations a similar trend is obtained for the QM and QM/MM methods [17-19]. In the medium and low regions (semiempirical and molecular mechanic parts) some perturbations were observed in the form of the following equations:Fig. 4. Calculated NMR anisotropy by QM and QM/MM methods for penicillin N (1), streptomycin (2), benzyl-penicillin (3), and kanamycin (4).
where
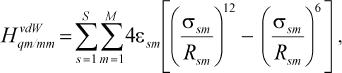 (2)
(2)where s is the number of atoms in the MM part and m the number of atoms in the QM part. The sigmasm and epsilonsm are experimental parameters;
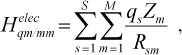 (4)
(4)where qs is atomic charge on MM atom, Zm is atomic charge on QM atom, and Rsm is the distances between particles. In the MM region, we use total strain energy in the form of:
ETotal = Sigma(Eb + Etheta + Ephi + Enb + Eepsilon + Ehb + Edelta + ...). (5)
Table 3. Comparison between resulting QM and
QM/MM isotropy, anisotropy, and chemical shift anisotropy asymmetry
(Etha)
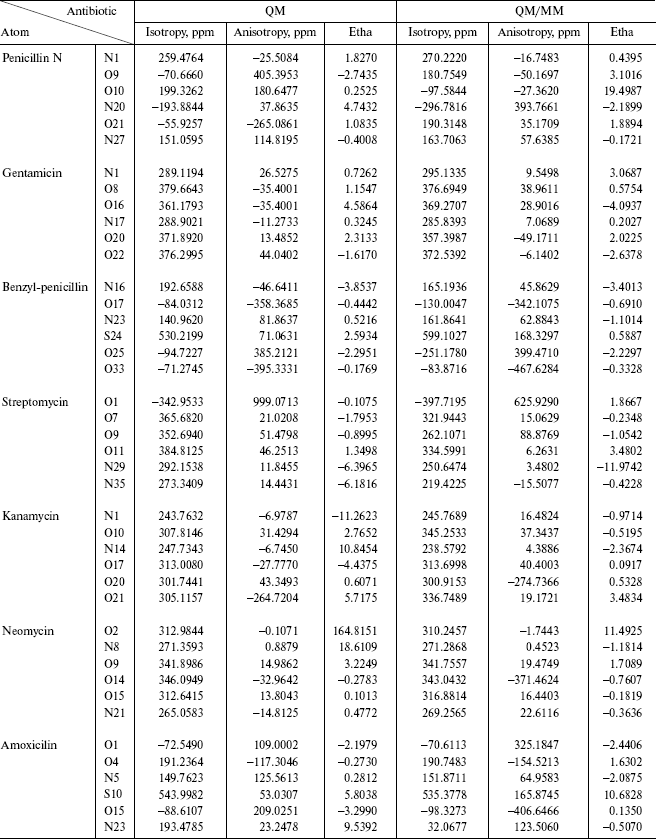
In this part of the calculations two dummy atoms (H) are entered in the molecule and the chemical environment of atoms differ with the primary structure. In the full ab initio method, the hydrogen and carbon atoms have similar chemical environment and their chemical shifts are approximately uniform. Therefore, simply we can see the effect of isolation of parts in NMR spectra. Usually the heavy atoms that contain electron pairs have high delta_values and display peaks.
The energy values for some different ab initio and DFT methods and the comparison between the QM and QM/MM methods are given in Table 4. As observed geometrical values are very close in the two methods and where the ab initio calculations are not possible, for example, in molecules consisting of 100 or greater number of atoms, we can use QM/MM results with complete assurance.
Table 4. Optimized structure of different
antibiotics with their energies (Hartree) by QM and QM/MM methods
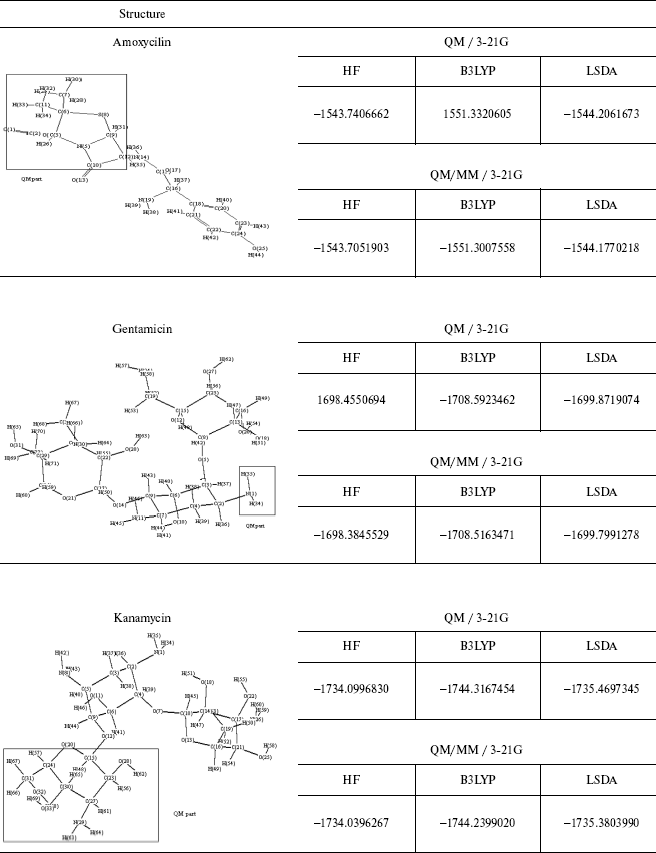
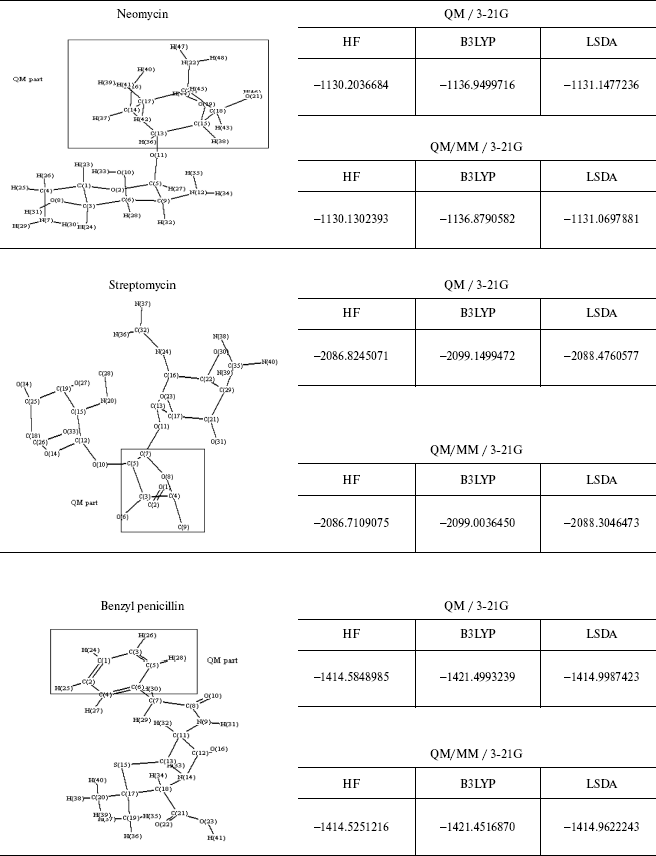
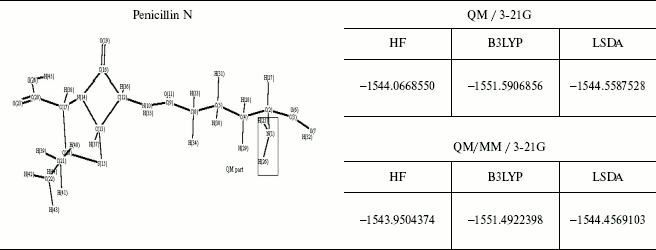
This brief review of the QM/MM approach has emphasized the variety of ways that QM and MM calculations can be combined. As may be clear from the number of variations that are possible it will probably be difficult to get exactly the same answer 5 with two separate implementations and like the force fields themselves the methodology will gradually gain acceptance on the basis of experience.
The QM/MM model for describing biomolecules, while successful, still requires further development which will lead to a better integration of the QM and MM formalisms by solving the problem of the QM/MM boundary in a general way. Thus it is expected that both the development and the application of QM/MM method will continue to expand strongly in the current decade and that the information obtained from QM/MM calculations will be essential for a deep understanding of biochemical processes. A number of other systems are currently under study with the new QM/MM methods that have been developed recently in this group. Implementations of the algorithm to calculate NMR chemical shielding tensors in the QM/MM framework makes it possible to study the chemical shift of specific group in biomolecules.
REFERENCES
1.Hart, J. C., Burton, N. A., and Hillier, I. H.
(1997) Chem. Commun., 1431-1432.
2.Haiyan Liu, Yingkai Zhang, and Weitao Yang (2000)
J. Am. Chem. Soc., 122, 6560-6570.
3.Vreven, T., Morokuma, K., and Frisch, M. J. (2003)
J. Comp. Chem., 24, 760-769.
4.Gherman, B. F., Goldberg, S. D., Cornish, V. W.,
and Friesner, R. A. (2004) J. Am. Chem. Soc., 126,
7652-7664.
5.Gascon, J. A., and Batista, V. S. (2003) Dep. Chem.
Yale University, P.O. Box 208107, New Haven, CT 06520-8107 (December 8,
2003).
6.Remko, M., van Duijnen, P. Th., and Marcel (2003)
Struct. Chem., 14, 271-278.
7.Roethlisberger, U., Vidossich, P., and Carloni, P.
(2003) Sci. Supercomput. Cineca, DOI:10.1388/SSC (2003)
432-436.
8.Yamada, A., Ishikura, T., and Yamato, T. (2004)
Proteins: Structure, Function, Bioinformatics, 55,
1063-1069.
9.Frisch, M. J., Trucks, G. W., Schlegel, H. B.,
Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Zakrzewski, V. G.,
Montgomery, J. A., Jr., Stratmann, R. E., Brent, J. C., Dapprich, S.,
Millam, J. M., Daniels, A. D., Kudin, K. N., Strain, M. C., Farkas, O.,
Tomasi, J., Barone, V., Cossi, M., Cammi, R., Mennucci, B., Pomelli,
C., Adamo, C., Clifford, S., Ochterski, J., Petersson, G. A., Ayala, P.
Y., Cui, Q., Morokuma, K., Malick, D. K., Rabuck, A. D., Raghavachari,
K., Foresman, J. B., Cioslowski, J., Ortiz, J. V., Baboul, A. G.,
Stefanov, B. B., Liu, G., Liashenko, A., Piskorz, P., Komaromi, I.,
Gomperts, R., Martin, R. L., Fox, D. J., Keith, T., Al-Laham, M. A.,
Peng, C. Y., Nanayakkara, A., Gonzalez, C., Challacombe, M., Gill, P.
M. W., Johnson, B., Chen, W., Wong, M. W., Andres, J. L., Gonzalez, C.,
Head-Gordon, M., Replogle, E. S., and Pople, J. A. (1998) Gaussian
98, Revision A. 7, Gaussian, Inc., Pittsburgh, PA.
10.Sherwood, P. (2000) Modern Methods and
Algorithms of Quantum Chemistry, John von Neumann Institute for
Computing, NIC Series, Vol. 3, pp. 285-305.
11.Scientific Computing and Modeling NV,
Vrije Universiteit, Theoretical Chemistry, De Boelelaan 1083, 1081 HV
Amsterdam, The Netherlands, ADF Program System Release, 2002.01.
12.Yamada, A., Ishikura, T., and Yamato, T. (2004)
Proteins: Structure, Function, and Bioinformatics, 55,
1070-1077.
13.Ditchfield, R. (1974) Mol. Phys.,
27, 789.
14.Cheesman, J. R., Frisch, M. J., Devlin, F. J.,
and Stephens, P. J. (1996) Chem. Phys. Lett., 252,
211.
15.MacWeeny, R. (1962) Phys. Rev.,
126, 1028.
16.Wolinsky, K., Hilton, J. F., and Pulay, P. (1990)
J. Am. Chem. Soc., 112, 8251.
17.Cui, Q., and Karplus, M. (2000) J. Phys. Chem.
B, 104, 3721-3743.
18.Molina, P. A., Sikorski, R. S., and Jensen, J. H.
(2003) Theor. Chem. Acc., 109, 100-107.
19.Warshel, A., and Levitt, M. (1976) J. Mol.
Biol., 103, 227.