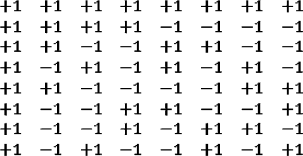Post-Reproductive Life Span and Demographic Stability
J. J. Mitteldorf* and C. Goodnight
Dept of Biology, Life Sciences Building, University of Vermont, Burlington VT 05405, USA; E-mail: josh@mathforum.org* To whom correspondence should be addressed.
Received April 30, 2013
Recent field studies suggest that it is common in nature for animals to outlive their reproductive viability. Post-reproductive life span has been observed in a broad range of vertebrate and invertebrate species. But post-reproductive life span poses a paradox for traditional theories of life history evolution. The commonly cited explanation is the “grandmother hypothesis”, which applies only to higher, social mammals. We propose that post-reproductive life span evolves to stabilize predator–prey population dynamics, avoiding local extinctions. In the absence of senescence, juveniles would be the most susceptible age class. If juveniles are the first to disappear when predation pressure is high, this amplifies the population’s risk of extinction. A class of older, senescent individuals can help shield the juveniles from predation, stabilizing demographics and avoiding extinction. If, in addition, the life history is arranged so that the older individuals are no longer fertile, the stabilizing effect is further enhanced.
KEY WORDS: menopause, aging, senescence, programmed aging, adaptive aging, evolutionDOI: 10.1134/S0006297913090071
Post-reproductive life span (PRLS) is common. It is not only human females that survive beyond menopause, but also whales [1], elephants [2], opossums [3], quail [4], parakeets [5], guppies [6], lab mice [7], the roundworm Caenorhabditis elegans [8], and even yeast [9]. There is evidence PRLS exists in the wild and not just in the lab [1, 5, 8, 10]. It is likely that this list is limited by the number of species that have been studied, and that the phenomenon of PRLS is actually ubiquitous in nature [10].
The only established theory for PRLS is the “grandmother hypothesis” [11], which posits that PRLS is adaptive because parents can assist their children in raising offspring. This model applies only to highly social animals. But PRLS is not restricted to social vertebrates for which this hypothesis might find plausible application. Even for humans, with their extraordinary life spans and social networks to nurture the young, the kin selection benefits of menopause have been shown to be inadequate compensation for the direct costs [12].
It is not possible to explain PRLS based on optimization of individual fitness. Clearly there is no benefit of PRLS to individual fitness, especially if, as is widely assumed, maintenance of the soma carries a significant metabolic cost that could have been expended in reproduction at an earlier age [13]. PRLS presents a challenge for any of the established theories of aging. Based on the assumption of life history tradeoffs that have come to define the field, Williams [14] once made the prediction that “There should be little or no post-reproductive period in the normal life-cycle of any species”. His reasoning was that PRLS represents a genetic cost with no offsetting pleiotropic benefit.
If, indeed, PRLS carries a significant cost in individual fitness, then attributing PRLS to an accident of history or development is not adequate; a general explanation for its existence and evolution is requisite. This benefit can only accrue to a larger selective unit than the individual. But group selection is widely perceived to be weaker and slower than individual selection [15]. What group benefit could compete with the direct cost of fertility loss? Analysis using multilevel selection theory [16] based on the Price Equation [17] only confirms the conclusion that the group benefit cannot overcome the individual cost.
But there are perspectives broader yet than the multilevel selection theory. In particular, the Price Equation assumes that the size of a metapopulation is stable, and that the sub-populations vary slowly compared to the time scale of one generation. This is not generally realistic. It may be that population dynamic changes occur on a time scale comparable to or faster than the time scale for changes in gene frequency. Hence extinctions can eliminate selfish traits more rapidly than individual selection can promote them within a subpopulation, explicitly violating Maynard Smith’s [15] assumption.
A metapopulation model in which the possibility of local extinction is explicitly incorporated makes different predictions from either classical population genetics or even multilevel selection theory [18]. The inexorable pressure to maximize individual reproduction is effectively countered by the lethal effect of unstable population dynamics when fertility rises too high [19, 20].
Although always controversial, group selection has a long history in biological thought, tracing back at least to Darwin [21]. The current controversy over the efficacy of group selection traces to the rejection of Wynne–Edwards’s [22] view of group selection by Maynard Smith, Williams and others [21]. It was May [23] who first analyzed natural populations as complex dynamical systems, and Gilpin [19] who developed an early computational model of a simple predator–prey system and first identified the potential for group selection to affect population dynamics. Thomas et al. [24] proposed that the reason chaotic population dynamics are not frequently observed in nature is that population chaos leads rapidly to extinction, resulting in a powerful group-selective force. Ferriere and Fox [25] emphasized that long-term evolution probably could not be understood without incorporating complex dynamics of populations. It is now widely agreed that natural population dynamics are generally more stable than naïve theory or laboratory models might suggest. But the field is dominated by a suspicion of group selection rooted in classical population genetic theory, which is premised on slowly changing gene frequencies in constant populations. Hence there has been a good deal of attention to the question whether population stabilization could evolve as an incidental by-product when life histories are individually optimized to respond to population density [26, 27]. This field is reviewed by Mueller [28].
Mitteldorf [29, 30] has argued that the broad phenomenology and genetic character of senescence could only have evolved as an adaptation, and that an adaptive theory of aging is required. He proposed a picture in which senescence rescues the population from chaotic dynamics leading to extinction [20], and demographic homeostasis becomes a major target of natural selection at the population level. In this context, Mitteldorf and Pepper [31] suggested that aging could be favored by selection at the population level due to its leveling effect on the death rate. Populations subject to aging are characterized by mortality rates that are steadier and more predictable, and the boom-bust cycles are consequently damped. Thus, even if aging tends to depress individual fitness and to lower average population levels, it may nevertheless be selected because it protects against local extinction when population levels swing low.
Here we focus on one aspect of aging as an adaptation for stabilizing population dynamics, the potential role of group selection acting on aging and PRLS in the prey species in a predator–prey dynamic (or similarly to host species in a pathogen–host system). We show that aging helps to stabilize population dynamics, and that PRLS may contribute to minimizing the individual cost of demographic homeostasis.
A MECHANISM STABILIZING POPULATION CYCLES
The very young are small and not yet fully developed. In the absence of aging, the youngest prey would be the most vulnerable to predation. But aging constitutes a steady decline in viability, assuring the existence of a group – the oldest, marginally viable individuals – that are more vulnerable than the young. It is this vulnerability of the older members of the population that stabilizes population dynamics by diverting the thrust of predation pressures away from the young and those in their prime reproductive years. (An extension of Gilpin’s [19] reasoning suggests that predators may even be co-adapted to avoid the youngest prey, even when they are easy marks, to focus instead on a senescent age class that has less impact on their future food pool.) Vulnerability of the young to predation is a destabilizing force in population dynamics, whereas vulnerability of the old to predation is a stabilizing force. A population in which the old are more vulnerable than the young is more robust against population cycling than the reverse situation, in which the young are most vulnerable.
Consider the population dynamics of an age-structured prey population in which predation is focused on the youngest age class. The declining phase of prey population occurs when predators are at a maximum. If it is the young that bear the brunt of the predation, the blow is more severe, and the decline more precipitous. Effective rates of reproduction may drop near zero as young are unable to mature. Later, when predators are at a minimum and prey population is expanding, population growth is accelerated by the fact that the population is dominated by young individuals that are no longer the target of intense predation. The population will be enriched in young, fertile individuals. Thus population cycles swing further in both directions, compared to the case in which predation is age-independent.
If predation is focused instead on the oldest segment of the population, then we expect the opposite to be the case. The oldest prey have already made their contribution to the next generation, so that expansion or contraction of this segment of the population has relatively less effect on population dynamics. If, in addition, the oldest prey are post-reproductive, then we expect this may be the best case for demographic stability, since the post-reproductive class may absorb predation with little effect on the birth rate.
In summary, a post reproductive, senescent age class becomes a demographic buffer for a population. In times of high predation they attract predators allowing the individuals in their prime reproductive years to reproduce and increasing the likelihood that the resulting young will survive. In addition, the post-reproductive senescent individuals will consume resources at population peaks, lowering the overall growth rate of the population; but they will be the first to starve and die when resources become scarce, again buffering the population. Importantly, such age-directed mortality during times of population decline will leave standing a population that is dominated by young and recently matured individuals, and that is a good demographic structure for rapid population recovery.
Review of the Lotka–Volterra model. The simplest (and historically the oldest) mathematical model of predator–prey population dynamics is the Lotka–Volterra model [32, 33]. The classic Lotka–Volterra model tracks just two variables, x and y, the total population levels for predator and prey species. Life history is not part of the model, and demographic profiles are not considered.
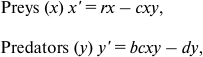 (1)
(1)where x′ is the rate of change of the prey population, y′ is the rate of change of the predator population, and r, b, c, and d represent parameters:
– r (reproduction) is the rate of exponential increase for the prey in the absence of predation;
– c (capture rate) controls the efficacy of predation;
– b (conversion parameter) predator’s efficiency in turning the prey’s biomass into its own;
– d (death rate) is the mortality per unit time for the predator species.
The Lotka–Volterra equations always produce stable limit cycles with amplitude depending on the initial conditions. The equations follow continuous variables, in which extinction (x = 0) is not a possibility; but some initial conditions lead to a dynamic range so wide that minimum populations are less than one individual. In nature, this is tantamount to extinction.
Model description. We have implemented a multi-site Lotka–Volterra model for the evolution of prey life histories. The predator population is just an aggregate number for each site, a function of time, while prey are tracked as individuals, each with a unique genome. There are n = 100 sites with prey migration among them. In each site, in each time step, prey may reproduce or they may succumb to predation. Predator population grows or declines in each time step depending on the number of prey captured. The target of our model is the evolution of prey life history, assumed to be under genetic control.
Prey genes outline a life history, defined as two curves: fertility and mortality as a function of age. In Lotka–Volterra dynamics, predation is the only source of mortality, so mortality is synonymous with vulnerability to predation. Genes control the timing of growth and maturity, as well as the decline of fertility and the increase in vulnerability that may occur at advanced ages. This allows for two kinds of senescence: a decline in fertility, and an increase in mortality. Five genes determine the fertility curve, and three more determine the mortality curve.
Five fertility genes:
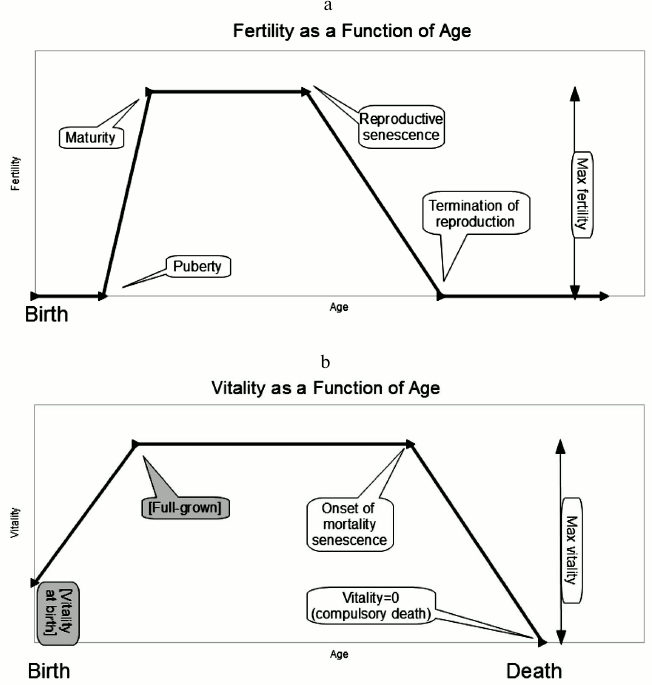
1) max fertility – the plateau level for the probability of reproduction, which attains between the ages of maturity and reproductive senescence specified by two other genes;
2) puberty – prey are born with zero fertility. At the age of puberty, their fertility begins to rise linearly toward a plateau value;
3) maturity – this is the age at which maximum fertility attains, and fertility ceases to rise;
4) reproductive senescence – the age at which fertility begins a linear decline;
5) termination of reproduction – the age at which an individual’s fertility has declined to zero, where it remains for the remainder of its life.
Three vitality genes:
1) vitality at birth – the inverse of this quantity is the prey’s vulnerability to predation when it is very young. Note that this is not necessarily the minimum vitality: in old age, senescent individuals can decline in vitality past this value. This is a fixed parameter, and not a gene because if it is permitted to evolve, it evolves upward without limit. It is our presumption that physical constraints, including size, dictate that vitality at birth is lower than in mature individuals;
2) full-grown – vitality rises linearly from birth to the age called full-grown, at which time it plateaus until the onset of senescence. This, too, is a fixed parameter and not a gene. If this quantity is permitted to evolve, it evolves to zero. It is our presumption that physical constraints limit the rate at which individuals can grow to full size;
3) max vitality – this is the maximal (plateau) value, corresponding to minimal vulnerability to predation, attained by the individual at the age called full-grown and persisting until it begins to decline, at an age called onset of mortality senescence.
Two fixed parameters:
1) onset of mortality senescence – the age at which vitality begins a linear decline (thus vulnerability to predation increases);
2) end-of-life – the age at which an individual’s vitality has declined to zero. At this point its vulnerability to predation is at a maximum.
The rate, at which prey die in each time step, is determined by the predator population, in accordance with the Lotka–Volterra equation. (In some versions of the model, prey may die of old age even when the predator population is too low to kill them.) The number of prey killed in each time step is proportional to the product of the number of predators and the number of prey. This fixed toll of predation is imposed on the prey in order of their vulnerability. Vulnerability is an individual characteristic that varies with age. In populations without senescence, the youngest are the most vulnerable, and they are the first targets of predation. Senescence can change this dynamic, so that old individuals are even more vulnerable than the newborns; hence they can effectively shield the young population from predation. This is crucial to the model, as it supplies the population benefit of senescence (balancing the individual cost).
The number of prey caught in each time step determines an incremental change in predator population. There is a constant parameter (called “cost of living”), which represents the number of prey each predator must capture at zero growth, where, presumably, starvation is balanced by reproduction. Growth or decline of the predator population is a linear function of the number of prey captured, with a slope b and an intercept CoL (for “cost of living”). These two free parameters represent characteristics of the predator biology.
Prey are tracked as individuals with genomes, but predator population size is tracked only as a floating point number. Floating-point representation of the predator population size insures that the predator population can become arbitrarily small (taking a long time to recover) but it can never reach zero. This is a standard assumption of Lotka–Volterra, responsible for the model’s characteristic behavior. Since the prey population is discrete, it is possible for the number at any site to drop to zero, whereupon it is re-seeded from another site. In this re-seeding as in migration, there is an equal probability for any prey individual at any site to migrate; hence sites that support a large population carry a selective advantage.
In each time step, each prey individual may reproduce (with mutation), with a probability fixed by its fertility. (Individual fertility is computed from age, according to a schedule dictated by the five genes described above.) Prey reproduction is optionally clonal or sexual (crossover within a single chromosome). With each reproduction, there is a large probability of small mutations, and also a small probability of large mutations at a single locus.
In each time step, the toll of prey captured is computed from the Lotka–Volterra equation, as a product of predator and prey populations. A value of vitality is computed for each prey individual, and prey are sorted from high to low vitality. The toll of predation is exacted from the list in order, starting with the weakest prey (low vitality). If the toll of predation is greater than the prey population, then the site suffers extinction (and may later be re-seeded by prey from another site); otherwise, the remaining prey grow older by one time step.
In each time step, each individual prey has a small, constant probability of migrating to another site, chosen at random. Predators do not migrate (nor do they have any individual attributes).
Note: Some idiosyncratic behaviors of the Lotka–Volterra equation carry over into our model. Crucially, the solutions can be either quite stable, with only small fluctuations in population, or arbitrarily turbulent. In the Lotka–Volterra model, increasing the reproductive rate r of the prey does not affect the steady-state value of the prey population, but the predator population increases in proportion. (This has been called the Paradox of Enrichment [34].) Thus it is roughly true that prey that evolve higher fertility and quicker maturation have an individual advantage locally; but sites characterized by high fertility do not have a group advantage compared to other sites.
HEURISTIC DESCRIPTION OF THE MODEL’S DYNAMICS
Intuition based on life history theory for individuals tells us that the life history should evolve so as to maximize individual reproductive value r1. We expect the genes for max fertility and max vitality (defined above, see Fig. 1) to evolve upward without limit; maturity should evolve toward age zero; and the two forms of senescence, fertility and vitality senescence should evolve toward later and later ages, delaying senescence without limit. The individual selection pressure within each group does indeed favor these outcomes, and when the model is run at a single site, this is exactly what happens.
1Of course, if r is taken as a generalized measure of the long-term growth in prevalence of a genotype, this becomes a tautology. However, it is customary to measure r over a single generation, where it can be calculated from LH (Life History) parameters. The assumption is that the local environment is changing slowly, so that the daughter generation replicates a similar dynamic to that of the parent. In conformance with this convention, we will use r to mean this function of LH, defined by the Euler–Lotka equation; but the process we model refers to a different story, in which short-term r is not a good predictor of long-term success, because of ever-changing demographic conditions.
Fig. 1. a) Five of the evolvable genes control parameters related to the fertility curve: these are maximum fertility, onset of fertility (“puberty”), maturity, reproductive senescence, and termination of reproduction. b) Three more evolvable genes control parameters related to what we call “vitality”, defined as the inverse of vulnerability to predation. These control the plateau (max) value of vitality, the time at which senescence begins to cause vitality to decline (linearly), and the time at which vitality reaches zero. In our model, this precipitates compulsory death even in situations where there is no predation. Vitality at birth and time to “full-grown” are not genes but parameters of the model. (If these parameters were permitted to evolve they adapt without limit toward ever-stronger youth.)
However, this direction leads to rapid extinction at the site. The predators are not evolving, and the predator population spikes after a time lag, driving the prey to local extinction. But even in the long run, there is little reward at the population level for increased reproductive value. The Paradox of Enrichment assures that higher prey productivity contributes to higher predator populations, but not higher prey populations. So the within-group selection for higher r is effectively opposed at the between-group level. Multi-level selection theory [16] tells us there will be a compromise.
There are many ways a life history can be moderated to stabilize Lotka–Volterra population dynamics and avoid extinction. All of these are viable from the standpoint of group selection. Our principal finding is that among these, life histories that involve substantial PRLS are not necessarily the most stable, nor even the ones that have the highest steady-state population levels; but PRLS is selected because it contributes to group-level stability with the least cost at the individual level.
SUMMARY OF RESULTS
We allowed life histories to evolve under the influence of individual selection for 1 to 3 million time steps. In some runs, a stable average life history emerged, but more commonly the dynamic continued to support a constantly shifting mix of life histories (defined as a curve of fertility and a curve of mortality). The only constraint was that mortality is high from birth to a certain age (“fullgrown”). This embodies the hypothesis that the very young are especially vulnerable, and it is a critical assumption of the model. If fullgrown is implemented as a gene, it evolves quickly to zero, and if vitality at birth is implemented as a gene, it evolves upward without limit.
We sampled a wide swath of parameter space, allowing the fertility and mortality curves that define a life history to evolve freely. In all cases, senescence was a feature of the resulting life history. In a large majority of cases, PRLS also characterized the evolved life histories.
We were looking to find a clear indication of an optimal life history to evolve for each set of environmental parameters. What we found instead was a great deal of stochastic scatter, even when the program was run for millions of time steps. The summary plots included in the “Results” section below are jagged and lines plotted for different parameter values sometimes cross one another. Is this real or an artifact of the model? We believe the absence of a clear optimum may correspond to features of the real world. PRLS in nature is not an essential feature of life history, under strong individual selection. It varies substantially in related species, and varies widely among different individuals of the same population.
In our model results, neither senescence nor PRLS were absolutely required to stabilize population dynamics. In some experiments, life histories were constrained so that no PRLS was allowed, but the shape of fertility and mortality curves was free to evolve in other respects. The phenotypes that evolved led to somewhat lower average population densities, and substantially more volatility, though these individuals were competitive in terms of growth rate (r). When a further constraint was added such that fertility could not decline with age, nor could mortality increase with age (no senescence), the results was to achieve demographic stability by delaying reproduction and lowering fertility. In terms of group selection, these runs produced super-competitors, with very long times between extinctions. However, individual competitiveness was drastically suppressed, with r values down by a factor five or more. These results help explain why the highest levels of senescence and PRLS were attained when migration rates were high, so that both group and individual selection were important.
RESULTS
The role of senescence and PRLS. Almost all evolved life histories included senescence, defined as an increase with age in vulnerability to predation. Most also included PRLS: fertility declines before mortality increases. Note that both of these are emergent results, not built into the model or required in any direct way. There are perfectly viable LHs (in the model) that include neither senescence or PRLS. It is possible to stabilize population dynamics by limiting fertility, or delaying reproductive maturity.
We actually did this by artificially constraining the LH parameters, so that there was no senescence. A stable population dynamic emerged, but the LHs that evolved could not compete with the LHs that evolved from the full model. When we left out PRLS, the difference was more subtle, but still the LHs so evolved lost in a (subsequent, binary) evolutionary competition to the ones that evolved from the full model that included PRLS.
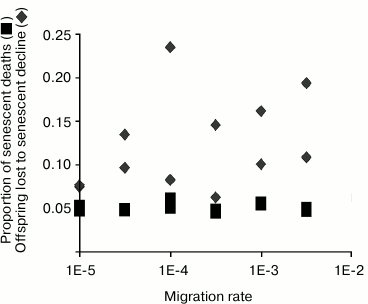
How to measure senescence. Effects of sex, epistasis, and migration rate. In summarizing results, we measure evolved senescence by the percentage of all deaths that are attributable to decreasing vitality. In other words, for each prey individual that has died, we ask whether it would have died had its vitality remained at maximum level, and not declined as a result of senescence (Fig. 2). Percentage of senescent deaths is our measure of senescence.
Fig. 2. Rate of migration is varied over three orders of magnitude, along the horizontal (x) axis. Vertical (y) axis is the proportion (senescent death) or number (offspring lost due to fertility decline). Squares plot evolved senescence, measured as the percentage of all prey deaths that can be attributed to senescent decline. Diamonds represent evolved PRLS, measured as the number of offspring an average individual forgoes because of fertility decline. See text for a full description of this statistic.
One advantage of using this measure is that it is dimensionless, and model-independent. Partially for this reason, it has become common to report this same measure in field studies of senescence in animal populations [35-38].
Our measure of PRLS in evolved LHs is the number of offspring that an average individual forgoes because of replicative senescence. We define lost fertility as a function of age to be the difference between maximum fertility and actual fertility at that age. Then forgone offspring is computed in our model as a time integral of lost fertility from the onset of replicative senescence to the actual time of death. (This definition is our own; there is no standard measure of PRLS in the literature.) In our evolved life histories, forgone offspring ranged typically from a few hundredths to a few tenths, representing a substantial sacrifice in individual fitness. For comparison, an average individual produces exactly one offspring in a lifetime.
Sex and epistasis were optional to the model, controlled by conditional compilation. Surprisingly, neither sex nor epistasis had much effect on evolutionary dynamics. Migration rate was controlled by a model parameter. Yet more surprisingly, migration rate did not play a major role. (We expect migration rate to control the balance between individual and group selection.)
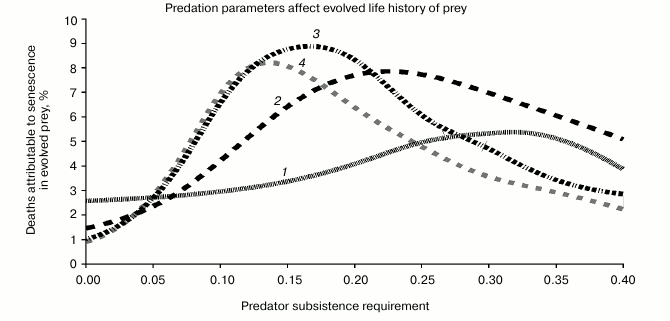
Effect of predation parameters on evolved prey life history. We found that the two parameters controlling predation were the strongest determinants of evolved prey life history. Recall that in Lotka–Volterra dynamics, predators are characterized by a population growth rate that is a linear function of the rate of prey consumption per predator. The slope of this line is b and the intercept is CoL. These are our two predation parameters. We found that the highest levels of senescence and of PRLS evolved for intermediate values of b and CoL.
In the Fig. 3, the x axis is CoL, and the different curves are parameterized by different values of b. The y axis is senescence (% senescent deaths).
Fig. 3. This sequence of plots shows how senescence in prey evolves in response to two behavioral variables in the predator. (i) The x axis represents “zero growth” nutritional requirement of the predator. If each predator consumes less than this amount, then the population is in decline, and if they consume more than this amount, their population is growing. (ii) How fast does the population grow or decline? The curves are indexed by a proportionality constant that connects the population growth rate to the rate at which predators are consuming prey (curve has been smoothed by a B-spline algorithm): 1) Predator R = 0.005; 2) 0.020; 3) 0.035; 4) 0.051.
DISCUSSION
There is substantial evidence of PRLS in nature and no viable explanation for it from individual selection – indeed, there can be none since PRLS adds nothing to individual fitness. Standard kin selection arguments (the “grandmother hypothesis”) are inapplicable to non-social species, and even for humans, they fail quantitatively [12]. From this alone, it follows that natural selection has not optimized individual fitness, as classically defined. Something important is missing from standard population genetic theory, and our hypothesis is that what is missing is the collective survival value of demographic homeostasis.
Organisms such as yeast and Caenorhabditis evince PRLS, though they offer no parental care. On the other hand, it is certainly suggestive that these two organisms have other life history adaptations specifically for the purpose of surviving deep cycles in the availability of food: yeast forms spores and worms form dauers.
Of the many group-selected benefits of PRLS, stabilization of population dynamics is likely the most potent, and certainly the quickest in action. Using an individual-based simulation based on Lotka–Volterra population dynamics, we have demonstrated the advantages to a prey species of maintaining in the population a reservoir of older, post-reproductive individuals that is most susceptible to predation.
Modeled in our experiment are two kinds of senescence: fertility decline and mortality increase. Our finding is that when the former precedes the latter (i.e. PRLS) in a prey population, the result, collectively, enhances the ability to sustain a population of predators in steady state, while minimizing the cost to individual fitness.
In recent years there have been numerous demonstrations that predator–prey population dynamics can be a strong driver of selection above the individual level [39-45]. But these results have not been assimilated by theorists. Internally driven population dynamics are rarely incorporated into traditional population genetics models.
PRLS is a particularly good candidate for a trait shaped by multilevel selection. After reproduction ceases individual fitness is by definition zero. For this reason the standard models of aging [14] suggest that under individual selection alone PRLS should disappear. Thus, the ubiquity of PRLS suggests that it is maintained by selection acting above the level of the individual.
In nearly all organisms it will be true that the juveniles will be more susceptible to predation and other forms of mortality than the adults will be. Our model shows that for prey populations in which juveniles are the most susceptible age class, the population dynamics can be stabilized only at great cost to individual fitness. Conversely, if there is an age class more vulnerable than the juveniles, population dynamics can be stabilized with less effect on individual r.
The inescapable fact that the young are small and vulnerable poses a dilemma for population stability. It must be assumed that there is already strong selection pressure to strengthen the youngest age class, but physical constraints on size and development limit the extent to which juveniles can be protected from predation. An alternative approach is to separate the young into a different niche, with different predators and food sources, and uncoupled ecological cycles. We speculate that this is a reason for distinct larval morphologies in (for example) many insects and amphibians [46, 47].
Alternatively, any solution that entails weakening some subset of the population until the young are no longer the weakest will be strongly opposed by individual selection. Aging and PRLS may be the solution to this dilemma that carries the least individual cost. Consider as an alternative the case where the highly susceptible group is genetically determined. Regardless of the genetics such a vulnerable group will be eliminated by individual selection. However, if every individual potentially goes through the susceptible stage, and if that susceptible stage occurs at the end of life, then the opposition of individual selection is minimized. It is a fundamental result of life history theory and a basic assumption of standard theories of aging that individual selection late in life is weak [48]. If this stage occurred following cessation of reproduction the individual selection, opposing it would be very nearly zero. Notice that this is analogous to the antagonistic pleiotropy model of aging [14]. In the antagonistic pleiotropy model, traits promoting reproduction early in life at the expense of survival late in life are favored because selection early in life is strong, whereas selection late in life is weak. Our hypothesis is similar except that the tradeoff is between the population level trait of demographic stability and the individual trait of reproduction late in life.
Predator–prey interactions are a near-universal feature of ecosystems, and hence a viable candidate for explaining the broad presence of senescence and PRLS in nature. Host–pathogen interactions can create very similar dynamics, further broadening the potential applicability of this model [40, 45]. When the population includes a range of susceptibility to infection, there is a constant presence of pathogens that helps to stimulate the development of young immune systems without overwhelming them with fatal disease. It is tempting to speculate that PRLS is able to stabilize population dynamics against a wider range of demographic forces. The case of predator species, for example, was considered previously [20].
REFERENCES
1.McAuliffe, K., and Whitehead, H. (2005) Trends
Ecol. Evol., 20, 650.
2.Packer, C., Tatar, M., and Collins, A. (1998)
Nature, 392, 807-811.
3.Austad, S. (1993) J. Zool. London,
229, 695-708.
4.Ottinger, M. A., and Balthazart, J. (1986) Horm.
Behav., 20, 83-94.
5.Holmes, D. J., and Ottinger, M. A. (2003) Exp.
Gerontol., 38, 1365-1375.
6.Reznick, D., Bryant, M., and Holmes, D. (2006)
PLoS Biol., 4, e7.
7.Gosden, R. G., Laing, S. C., Felicio, L. S.,
Nelson, J. F., and Finch, C. E. (1983) Biol. Reprod., 28,
255-260.
8.Goranson, N., Ebersole, J., and Brault, S. (2005)
Evol. Ecol. Res., 7, 325-333.
9.Minois, N., Frajnt, M., Wilson, C., and Vaupel, J.
W. (2005) Proc. Natl. Acad. Sci. USA, 102, 402-406.
10.Cohen, A. A. (2004) Biol. Rev. Camb. Philos.
Soc., 79, 733-750.
11.Lahdenpera, M., Lummaa, V., Helle, S., Tremblay,
M., and Russell, A. F. (2004) Nature, 428, 178-181.
12.Kachel, A. F., Premo, L. S., and Hublin, J. J.
(2011) Proc. Biol. Sci., 278, 384-391.
13.Kirkwood, T. (1977) Nature, 270,
301-304.
14.Williams, G. (1957) Evolution, 11,
398-411.
15.Maynard Smith, J. (1976) Q. Rev. Biol.,
51, 277-283.
16.Wilson, D. S. (1997) The American
Naturalist, 150 (S1), S1-S21.
17.Price, G. R. (1970) Nature, 227,
520-521.
18.Wright, S. (1931) Genetics, 16,
97-159.
19.Gilpin, M. E. (1975) Group Selection in
Predator–Prey Communities, Princeton University Press,
Princeton.
20.Mitteldorf, J. (2006) Evol. Ecol. Res.,
8, 561-574.
21.Borrello, M. (2010) Evolutionary Restraints:
the Contentious History of Group Selection, University of Chicago
Press, Chicago.
22.Wynne-Edwards, V. (1962) Animal Dispersion in
Relation to Social Behavior, Oliver & Boyd, Edinburgh.
23.May, R. M. (1973) Stability and Complexity in
Model Ecosystems, Princeton University Press.
24.Thomas, W. R., Pomerantz, M. J., and Gilpin, M.
E. (1980) Ecology, 61, 1312-1320.
25.Ferriere, R., and Fox, G. A. (1995) Trends
Ecol. Evol., 10, 480-485.
26.Heckel, D. G., and Roughgarden, J. (1980)
Proc. Natl. Acad. Sci. USA, 77, 7497-7500.
27.Turelli, M., and Petry, D. (1980) Proc. Natl.
Acad. Sci. USA, 77, 7501-7505.
28.Mueller, L. D., and Joshi, A. (2000) Stability
in Model Populations. Monographs in Population Biology (Levin, S.
A., and Horn, H. S., eds.) Vol. 31, Princeton University Press,
Princeton.
29.Mitteldorf, J. (2004) Evol. Ecol. Res.,
6, 1-17.
30.Mitteldorf, J. (2010) in Approaches to
the Control of Aging: Building a Pathway to Human Life Extension
(Fahy, G. M., et al., eds.) Springer, New York.
31.Mitteldorf, J., and Pepper, J. (2004)
Selection in Ecosystems, Fifth Int. Conf. on Complex Systems,
NECSI, Boston, MA.
32.Lotka, A. J. (1925) Elements of Physical
Biology, Williams and Wilkins, Baltimore.
33.Volterra, V. (1931) in Animal Ecology
(Chapman, R. N., ed.) McGraw-Hill.
34.Rosenzweig, M. L. (1971) Science,
171, 385-387.
35.Ricklefs, R. (1998) Am. Nat., 152,
24-44.
36.Bonduriansky, R., and Brassil, C. E. (2002)
Nature, 420, 377.
37.Bonduriansky, R., and Brassil, C. E. (2005) J.
Evol. Biol., 18, 1332-1340.
38.Nussey, D. H., Froy, H., Lemaitre, J. F.,
Gaillard, J. M., and Austad, S. N. (2012) Ageing Res. Rev.,
12, 214-225.
39.Nudds, T. (1987) in Wild Furbearer
Management and Conservation in North America (Novak, M. B., Obbard,
J., M., and Mallock, B., eds.) Ontario Trappers Assn., Toronto.
40.Rand, D. A., Keeling, M., and Wilson, H. B.
(1995) Proc. Roy. Soc. B, 259, 55-63.
41.Abrams, P. A. (2000) Ann. Rev. Ecol. Sys.,
31, 79-105.
42.Cuddington, K., and Yodzis, P. (2002) Am.
Nat., 160, 119-134.
43.Pels, B., de Roos, A. M., and Sabelis, M. W.
(2002) Am. Nat., 159, 172-189.
44.Pepper, J. W., and Smuts, B. B. (2002) Am.
Nat., 160, 205-213.
45.Rauch, E. M., Sayama, H., and Bar-Yam, Y. (2003)
J. Theor. Biol., 221, 655-664.
46.Loreau, M., and Ebenhoh, W. (1994) Theor.
Popul. Biol., 46, 58-77.
47.Moll, J. D., and Brown, J. S. (2008) Am.
Nat., 171, 839-843.
48.Medawar, P. B. (1952) An Unsolved Problem of
Biology, Published for the College by H. K. Lewis, London.
APPENDIX
Detailed description of the model. There are n = 100 sites, with no geometrical relationship to each other, so that migration to any site is just as likely as any other. The population count of predators is modeled as a floating-point number at each site. Prey are tracked individually, each with 8 life history genes, a birth date, a probability to reproduce and to die in each time step. Prey are characterized by two calculated quantities: their vulnerability to predation, and their fertility, which are computed from their age in accordance with a prescription specified in their genes.
Genes are represented as unsigned bytes, range 0-255. This range is scaled proportionately into a range that is determined from experience to be wide enough to encompass all evolved possibilities, but not much wider. For the genes that specify an age marker (puberty, maturity, onset of reproductive senescence, termination of fertility; onset of mortality senescence, end-of-life) the range is mapped onto a difference between that age marker and the previous one. For example, the maturity gene specifies a number of time steps after puberty. This arrangement assures that the temporal order of the life history inflection points is not changed by mutation.
In each time step, a toll of prey captures is computed from the product of the predator “count” (a floating point number) and the actual count of prey. For each prey, a vulnerability is computed from its age and its life history variables. Prey are ranked by vulnerability, and the toll is exacted from the prey population, in order, eliminating a number equal to the (rounded) toll of prey individuals from the population.
Each prey is afforded the opportunity, with a small probability, to migrate to another site, randomly selected.
Each prey is then given a chance to reproduce, and its probability of reproduction is calculated from its age and life history characteristics. (In runs with sex (see below), the prey agents are randomly ordered, then each individual that is selected to reproduce does so twice, once with the previous selected agent and once with the subsequent selected agent in line. Thus each selected reproducer contributes, on average, half its genes to two offspring.)
Finally, the count of predators is updated in accordance with the Lotka–Volterra equation, based on the number of prey captures. Below a threshold of prey captures per predator, the predator population will decrease; while above that threshold, the number of predators increases.
If the count of prey has fallen to zero, a random prey is selected from the aggregate prey population of all sites, and this agent reseeds the empty site. Sites with larger prey populations have a proportionately larger probability both of infiltrating an existing site or seeding an empty site.
Epistasis option. In the default version of the model, each gene is associated directly with a life history parameter. But in a variation, maximal epistasis is included: each gene contributes equally and independently to all life history variables. Specifically, a matrix composed of +1 and –1 entries was constructed, with each line independent of all others:
Each life history genome, regarded as a vector, is multiplied by this matrix. Each of the 8 numbers thus derived is equally dependent on each of the 8 genes. The results are re-scaled, as before, to determine the 8 life history parameters (puberty, maturity, onset of reproductive, etc.).
Though the mathematical schema was intriguing, the results, as reported above, varied little from the results with no epistasis. This came as a surprise to both authors, who believed, in general that epistasis favors the evolution of altruism. The unexpected result was put aside for future investigation.
Sex option. In most runs, reproduction is clonal (with mutation), but sex is a model option. Sex is implemented with monoecious individuals. Each act of reproduction involves two individuals. Each of the offsprings’ 8 genes is derived, with equal probability, from each of the two parents. The situation corresponds to maximal crossover.
The range of life histories that evolved with sex was not noticeably different from the results without sex. The reason for this was not determined, but left for future investigation.